用“定—变—等”思维解答数学问题

张生杰

（贵州省黔西县铁石中学，贵州 毕节 551511）

“数学数学，叉叉角角，老师难教，学生难学。”这是我读中学时，我的数学老师第一堂课开场语。今天，我从教数学学科二十载，这首打油诗记忆犹新。回顾这二十年教育实践活动，思之所悟：用“定—变—等”思维模式解答数学问题，数学并不象我的中学数学老师说的那么难，师生还可以享受学习数学的乐趣。

用“定—变—等”思维解答应用题

应用题是数学学科中极其重要的教学内容，是针对培养学生思维能力，灵活运用所学知识而设计编排的，是学生应用所学知识解决生活中实际问题的具体实践。学生通过解答应用题，可以感受到数学源于生活，体验学习快乐，感受知识给生活带来的无穷魅力。但是，学生对应用题这一知识点都存在畏惧心理，因此解答应用题没有达到理想效果。其实，利用“定—变—等”思维模式来解答，师生同感轻松。

一道应用题，不论编者设计得多么复杂，内容都蕴含了三个量，即：定量、变量、等量。定量是应用题中不变化的量（常量），是解答应用题必须条件；变量就是应用题中变化的量，也是应用题中最难把握的量，它的变化范围体现了知识面的广度和深度，决定应用题难易程度；等量就是应用题中相等的量，不论应用题所蕴含关系有多复杂，一定存在相等关系的量，否则，应用题就没有人能解答出来。

要轻松解、准确答应用题，就必须先把这“三个量”准确列出来，综合数据列出等式或方程，准确计算，问题迎刃而解。以两例而析“定—变—等”思维模式解答应用题。

北师大版九年级数学上P55习题2.10第3题：

某市2011年年底自然保护区覆盖率（即自然保护区面积占全市国土面积的百分比）仅为4.85%，经过两年努力，该市2013年年底自然保护区覆盖率达到了8%。求该市这两年自然保护区面积年均增长率（结果精确到0.1%）

第一 找定量：

①全市国土面积：设为A

②年均增长率：设为x

③2011年自然保护区覆盖率：4.85%

第二 找变量：

①2012年自然保护区面积

②2013年自然保护区面积

第三 找等量

即：2011年自然保护区面积=4.85%A

即：2012年自然保护区面积=2011年自然保护区面积×年均增长率+2011年自然保护区面积=4.85%Ax+4.85%A=4.85%A（x+1）

即：2013年自然保护区面积=2012年自然保护区面积×年均增长率+2012年自然保护区面积=4.85%A（x+1）x+4.85%A（x+1）

=4.85%A（x+1）2

问题得到解决。从此题解答得出这类试题解答公式，若第一年数据为a，年均增长率不变，经过两年增长后达到b，则可用：a(1+x)2=b求解。

第二例 本校九年级月考试题：

商场将进价为2000元/台的冰箱以2400元/台的价格出售，平均每天能售出8台。为了促销，商场采取适当的降价措施。调查表明：这种冰箱的售价每降低50元，平均每天就能多售4台，商场要想在这种冰箱销售中每天盈利4800元，同时又要使消费者得到更多实惠。每台冰箱应降价多少元？

第一 找定量：

①进价：2000元/台

②售价：2400元/台

③利润;2400-2000=400元/台

④销售量：8台/天

第二 找变量

①降价50元/台 多销售4台/天

即：利润为（400-50）元/台 销售量为（8+4）台/天

第三 找等量

降价后每台利润×降价后每天销售量= 4800

问题得到解决。

用“定—变—等”思维解答几何问题

基于初中学生思维发展模式，初中数学中编排几何内容，用于培养训练学生逻辑思维能力。解答几何问题跟语文写作文一样，需要积累丰富的基础知识，同时也需要语言逻辑表达。几何问题是告诉正确的结论，要求解答者通过所学知识书写处证明过程，完成结论证明。以北师大版九年级下册数学P121第14题为例解析“定—变—等”思维模式。

已知：如题，P为⊙O外一点，PA，PB为⊙O的切线，A和B为切点，BC为直径。求证：AC//OP

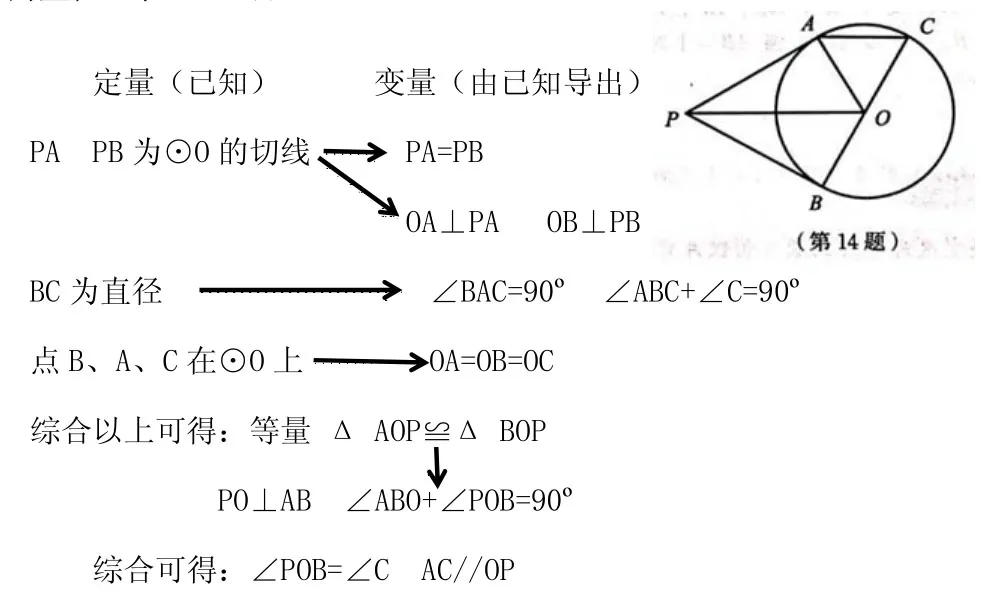
结论得到证明

提高解答数学问题质量，就要准确无误找出试题中关键量，可以考虑用“定—变—等”思维模式，简单、明了、准确地把问题中定量、变量、等量之间的关系呈现，为解答者准确无误提供解决问题方向。

总之，教无定法，贵在得法。伟大的教育家陶行知先生说：“教的方法要根据学的方法。”每一位教育者都具有自己最有效的教育教学模式。愿教育人尽显智慧，为给受教育者提供更优质、高效的服务。