几何画板演示动点轨迹 扫清学生空间想象盲区

张建芬

摘 要：在初中数学教学中，动点问题，常常作为考查学生学习能力和思维发展水平的中考压轴题，需要学生理解图形在不同位置的情况，在变化中找到解决问题的办法，因此，常常成为学生学习的难点所在。而几何画板被誉为“二十一世纪的几何点金石”，它以直观、简洁、动态的表现来解决动点难题，能帮助学生深刻理解，收到很好的效果。本文重点研究的是如何利用几何画板，更清晰直观地观察动点运动轨迹。

关键词：动点问题;几何画板;数形结合

一、 背景分析

（一） 知识背景与学生学情分析

1. 本课是中考第二轮复习时的一节专题复习课，学生已经复习完基础知识，基于对函数图像与方程有了较好的理解和运用的前提，而学生在解综合性的“动点问题”中有以下几个方面的困难：（1）不会分类讨论。（2）无法熟练地数形结合。（3）添加辅助线。因此安排了这样一节应用信息技术展示动点问题的专题课。

2. 在现代社会，电脑已经深入渗透到了学生的日常生活，更是走进了常规课堂，传统数学教学，老师在讲课时无法动态演示给学生观看图形变换过程，这对学生知识点的理解也是有阻碍的，随着科技的发展，促使了像几何画板等教学工具的产生。“动点问题”具有较强的综合性，对学生的能力有较高要求，学生往往感觉上课能听懂但自己做题时就无法入手。运用几何画板将“动点问题”动态展现出来，能使动点问题更加具体化，便于学生对于这类问题的理解，使学生的数学解题能力不再停留在简单的模仿阶段，从而对于学生提高数学成绩有深远的、重要的影响。

（二） 教材分析

现行的教材体系，基本都是新课标颁布实施以后的新编版本，由于新课标的实施，初中数学教材增加了图形运动的相关内容，其基本理念对近几年数学命题产生了重大影响，其中“动点问题”成为中考数学中的常客。它通常是中考的拉分题，更加综合地考查学生数学解题思想的运用能力。为了落实让数学的教与学贴近生活、贴近现实，增强学以致用、强化体验等新课程理念，顺应素质教育的要求，我今天选择了“几何画板演示动点轨迹，扫清学生空间想象盲区”这节课。

（三） 学生需求分析

1. 时代的进步，科技的提高，学生的学习方式也应该顺应改革不断完善，向多样化、自主性、探究式的方向转变。所以教材体现时代特征，是对传统教学的不断改进，值得我们响应与附和。

2. 利用电脑软件解决学科问题，特别是数学问题，学生已经司空见惯、耳闻目睹，面对陌生的数学问题或陌生的电脑软件，学生在心理上并无恐惧感，相反，在老师的推荐、带动和指导下，还能激发他们的好奇心和求知欲望，甚至能够激发他们对动点问题的尝试和探究的潜能。

因此，设置这样的一节专题课，不仅是要增强学生掌握现代信息技术的意识，也是在强化对新课程理念的导向，更是对教师自身学习与探究能力的挑战、检验与鞭策。

二、 实践举措

（一） 教学目标的设计

1. 知识定位

借助《几何画板》来探究有关动点的轨迹问题，从新的视角审视轨迹问题的本质;认识圆的几何属性在探究过程中的完美运用。

2. 能力定位

让学生从认识→理解→实践，提升学生解动点问题的能力，加强新时代背景下学生信息技术的基本功;培养学生探究数学知识，开阔视野，激发创新潜能。

3. 情感导向

让学生直观地感受点的运动轨迹，从本质上理解点的运动是怎么形成的，把知识教给学生，把能力传授给学生;投其所好，实施快乐教学，实现愉悦学习;师生共同提高，提升“数学”品味。

（二） 教学目标的实现

（三） 教法：演示法、指导法。

（四） 学法：实践法、探究法（“动手”学习，亲历体验）。

（1） 课前准备：选题，选了在本次月考中几乎全军覆没的一道题，然后用《几何画板》制作动态图像。

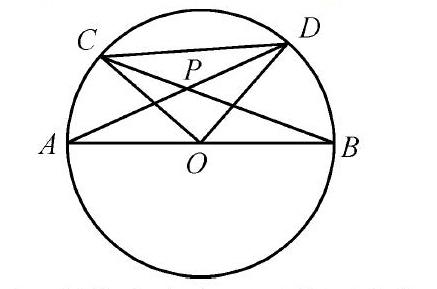
【例】如图，△COD是等腰直角三角形，当它从OA与OC重合位置开始顺时针旋转90°时，求点P经过的路径长。

在几何画板中，制作向大家展示等腰直角三角形绕点O旋转的动画，只要用鼠标选中C点，然后向右拖动鼠标，就可以观看到等腰直角三角形△COD绕点O顺时针旋转90°的整个过程。选中点P，并选择显示中的追踪，就可以清楚地看到点P运动的轨迹，是经过点A、P、B的弧。

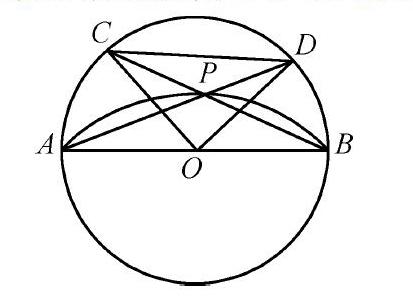
【配套练习题】如图，AB是圆O的直径，点C是半圆弧的中点，点P在弧BC上运动，CD垂直CP交AP于点D，求BD的最小值。

在几何画板中，制作向大家展示点P在弧上运动的动画，只要用鼠标选中点P，然后向右拖动鼠标，就可以观看到点D运动的整个过程。选中点D，并选择显示中的追踪，就可以清楚地看到点P运动的轨迹，是经过点A、D、C的弧。

（2） 课程开始：和学生一起理解题意，分析条件，得出结论。

【例】如图，△COD是等腰直角三角形，当它从OA与OC重合位置开始顺时针旋转90°时，求点P经过的路径长。

引导：△COD旋转的起始位置是哪里？此时点P的位置在哪里？

答：起始位置是点C在点A处，此时点P和点A重合。

引导：△COD旋转的终点位置是哪里？此时点P的位置在哪里？

答：终点位置是点D运动到点B处，此时点P和点B重合。

引导：你们能找到一个△COD旋转过程中的任一点位置吗？此时点P的位置在哪里？

答：题图的位置就可以。

引导：你们猜测点P的轨迹是一条什么线？

答：学生A：曲线。学生B：圆弧。学生C：折线……

师：到底是一条什么线，让几何画板给我们展示一下。

在几何画板中，制作向大家展示等腰直角三角形绕点O旋转的动画，只要用鼠标选中点C，然后向右拖动鼠标，就可以观看到等腰直角三角形△COD绕点O顺时针旋转90°的整个过程。选中点P，并选择显示中的追踪，就可以清楚地看到P点运动的轨迹，是经过点A、P、B的弧。

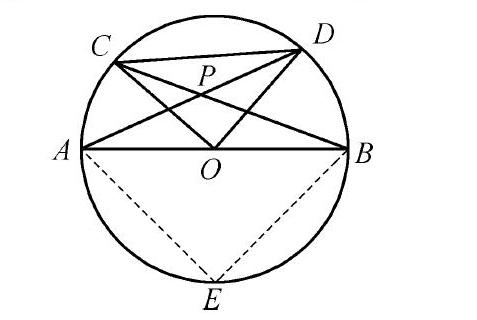
猜测是圆弧线后，给出证明∠APB始终为135°，确定点P在以弧AB的中点E为圆心，EA为半径的弧AB上，然后计算出轨迹的长。

给出配套练习，让学生尝试解答：

【配套练习题】如图，AB是圆O的直径，点C是半圆弧的中点，点P在弧BC上运动，CD垂直CP交AP于点D，求BD的最小值。

在几何画板中，制作向大家展示点P在弧上运动的动画，只要用鼠标选中点P，然后向右拖动鼠标，就可以观看到点D运动的整个过程。选中点D，并选择显示中的追踪，就可以清楚地看到点P运动的轨迹，是经过点A、D、C的弧。

三、 成效与反思

通过几何画板，在讲解动点问题时，就不再是纸上谈兵，可以实战演练给学生们观看，从而知道每个点的运动轨迹，这样就可以更好地进行讲解。学生们在面对动点运动的过程时也十分有興趣，觉得很神奇，运用几何画板，可以让学生在课堂上充分活动起来，课堂气氛活跃起来，让学生非常直观地得到结论，把教师的“教”与学生的“学”有机地结合起来，使学生真正成为学习的主人，让教师真正成为教学的引导者。而且对于动点问题，原先学生由于空间想象能力匮乏，始终没有在脑海中有过如此具体的动点的轨迹，几何画板让他们有了切实的经验，在今后遇到的问题中，可以有效地应用。美中不足的是，考试时并没有几何画板这样的工具，所以在几何画板演示之前，应该引导好学生，使得他们有充分时间进行空间想象能力的锻炼，这样，几何画板给他们的具体实践过程，才能真正起到作用。

参考文献：

[1]陶维林.几何画板实用范例教程（第3版），清华大学出版社出版，2013（9）.

[2]方其桂主编，周红文，朱俊杰.POD——几何画板4——课件制作方法与技巧，人民邮电出版社出版，2004（1）.