浅谈数学文化视角下的命题研究与教学建议

黄雪林

摘 要：教育部颁发的《普通高中数学课程标准（2017年版）》指出，数学文化是指“数学的思想、精神、语言，方法，观点及其形成和发展;还包括数学在人类生活，科学技术，社会发展和与数学相关的人类活动中的贡献和意义。”。数学文化对数学教育的重要作用已经引起了广大一线数学教师和学者专家们的关注。本文就研究2008～2018十余年的高考数学文化题的命题背景分析为切点浅谈数学文化视角下的命题研究和教学建议。

关键词：数学文化;数学核心素养;命题研究

我国在20世纪30年代就已经出现了数学文化的研究观点，北京大学教授孙小礼在《数学与文化》中指出“数学的出现及发展，是现代文化获得形成的主要力量”。“普通高中课程纲要”明确指出“数学文化应纳入数学教学活动。在教学活动中，教师应有意识地将相应的教学内容结合起来，将数学文化渗透到日常教学中，引导学生了解数学文化的发展。理解数学在科学技术，社会发展中的作用，认识数学的价值，提高学生的科学精神，应用意识和人文素养;将数学文化融入教学能激发学生学习数学的兴趣，帮助学生进一步了解数学有利于开放学生的视野，提高数学的核心素养。”以数学文化视角命制的数学题渗透了数学文化;关注社会发展，注重引导考生运用数学知识解决生活实际问题，笔者相就数学文化视角下谈谈命题研究与教学建议。

一、 数学文化命题的特征分析

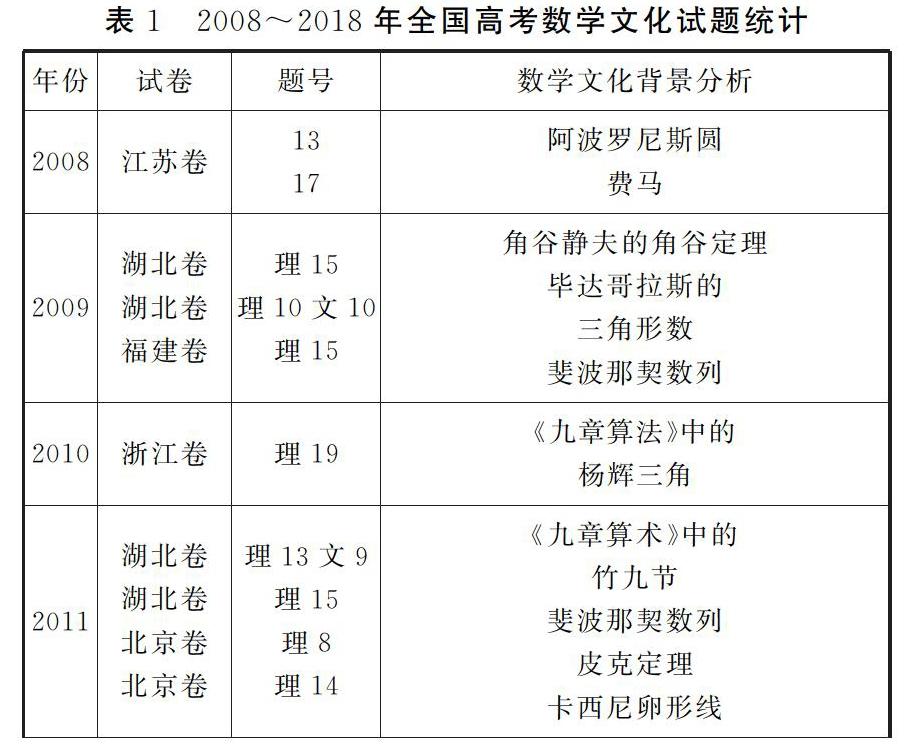
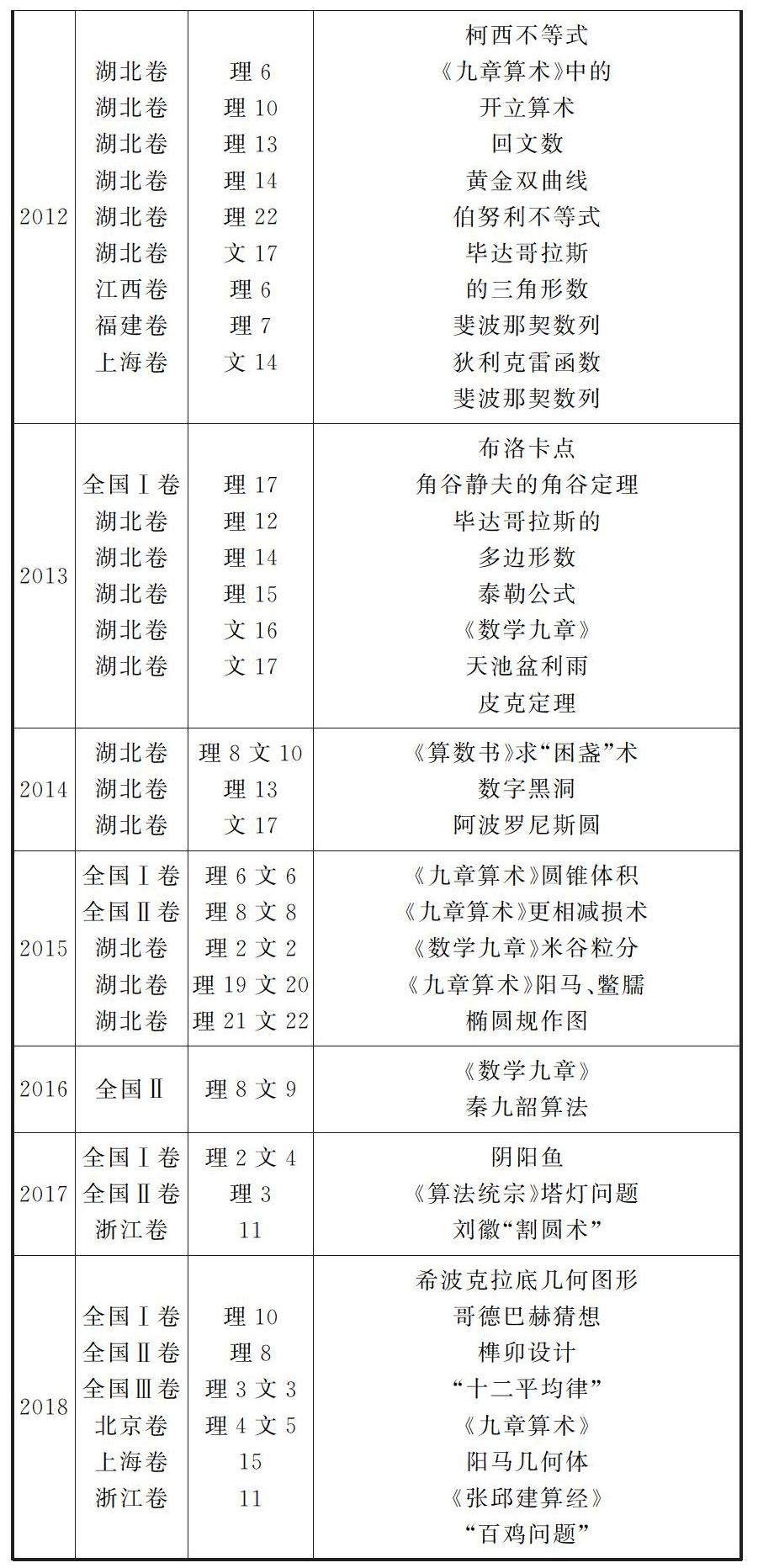
笔者对2008年至2018年十余年的高考试卷进行了统计，其中全国卷从2013年开始出现单独以数学文化视角命制的试题，在2015年全国Ⅰ卷和全国卷Ⅱ的文、理试卷都出现了以数学文化背景命制的试题，数学文化视角的数学试题引起重视并在之后的每一年的全国卷中都有出现。为了更直观从数学文化视角研究全国各地高考数学新课标文、理试卷中的相关背景下的试题笔者列表如下（表1）：

从上述统计结果中可以看出以数学文化视角命题的试题在全国卷的文、理科试卷中出现的频次较为均衡，但是在地方卷中就更为偏爱理科卷了。从知识点的分布来看，数学文化视角命制的题目较多的涉及立体几何（尤其是体积和表面积的计算）、平面解析几何（阿波罗尼斯圆以及东西方的历史名人的重要数学思想和数学史上著名的几何证明题为主）、算法程序框图（秦九韶算法和更相减损术等传承我国数学文化的素材）、数列（斐波那契数列等）、函数（狄利克雷函数等）。其中几何图形的体积计算，平面图形与概率结合面积计算，算法程序框图和数列的命题比重也较其他知识点要大。命题形式基本以选择题和填空题出现，在解答题中数学文化视角的试题较少涉及，并且表现形式也不如选择题和填空题出现的显而易见，一般会以较为含蓄的形式出现。

（一） 数学文化题的素材来源分析

十余年的数据分析为我们对数学文化视角的试题题目进行素材来源分析提供了便利的条件，笔者从数学文化背景分析数学文化题主要素材来源分为：

1. 源自数学名题的数学文化试题

以数学史中的数学真题名题为背景的试题基本都是具有数学问题的原型的，命题基于对原型本身进行一定的改编，主要改编方式以下三种形式为主：再现数学名题、对条件或目标进行改编、将结论或方法進行迁移。其中以我国数学史的数学名题很大一部分是取自《九章算术》《数学九章》《张邱建算经》等我国古代数学名著中的真题名题，基于数学文化多元化特征外国古代数学文化也备受命题者青睐，同样也以数学名题再现的形式出现为主，重现了古代数学家重要成果的发现思维过程。

【2018年浙江卷11】我国古代数学著作《张邱建算经》中记载百鸡问题：“今有鸡翁一，值钱五;鸡母一，值钱三;鸡雏三，值钱一。凡百钱，买鸡百，问鸡翁、母、雏各几何？”设鸡翁，鸡母，鸡雏个数分别为x，y，z，则x+y+z=1005x+3y+13z=100，当z=81时，x=    ，y=    。

分析：这是一道取自《张邱建算经》中的原题，采用的是文言文的形式并且还用方程把文言文进行了数学翻译，题目的命制属于直接再现原题并对目标进行改编相结合的方式。为学生提供了的文言文形式的数学名题的同时又解除了阅读障碍，充分的考察了学生用数学知识解决数学问题的能力。

【2018年上海卷15】《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马。设AA1是正六棱柱的一条侧棱，如图1，若阳马以该正六棱柱的顶点为顶点、以AA1为底面矩形的一边，则这样的阳马的个数是（  ）

A. 4

B. 8

C. 12

D. 16

【苏州市2018～2019学年第一学期学业质量阳光指标调研卷高二数学9 】《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年。例如：“堑堵”指底面为直角三角形，且侧棱垂直于底面的三棱柱;“阳马”指底面为矩形，一侧棱垂直于底面的四棱锥。如图2，在“堑堵”ABC-A1B1C1中，AC⊥BC，若“阳马”B-A1ACC1的体积为20cm3，则“堑堵”ABC-A1B1C1的体积为   cm3。

分析：这两道题都是以《九章算术》中的阳马、堑堵几何体为命题背景，是属于典型的对条件或目标的改编，包含了对已知条件的改编、所求目标的改编、同时改编条件和目标。这两题的背景设计相似问题设计方向却是完全不同，2018年上海卷15题涉及的考点是空间点、线、面的关系，苏州市2018～2019学年第一学期学业质量阳光指标调研卷高二数学9题考查的是空间几何体的体积的求解。在弘扬中国传统文化的同时，考察了学生的空间想象能力，开拓了学生的视野，践行了数学核心素养。

2. 源自文化事物的数学文化试题

选择源于文化符号、文化物品等文化事物的数学文化视角命制的试题，一般以展现数学美学为主题方向。数学美所体现的美学维度是精神空间上美，区别于自然美和艺术美，数学美学体现为抽象性、严谨性及冷峻而含蓄性的理性美。

数学美学主要表现为几何图形的结构美、数学符号语言的简洁美还有数学逻辑思维的严谨美。数学美的特征为和谐性和奇异性。数学家大会的会标（赵爽弦图）、希波拉克底研究的几何图形、传统太极图中的阴阳鱼等等，都是着眼于数学文化美学的渗透。实现对研究对象的理解抽象出数学问题，真正学会用数学的眼光观察世界，用数学的思维来思考世界，用数学的语言来表达世界。

【2017年全国卷Ⅰ理2文4】如图3，正方形ABCD内的图形来自中国古代的太极图。正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是（  ）

A. 14

B.π8

C. 12

D.π4

【2018年全国卷Ⅰ理10】如图4来自古希腊数学家希波克拉底所研究的几何图形。此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC。△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ。在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为p1，p2，p3则（  ）

A. p1=p2

B. p1=p3

C. p2=p3

D. p1=p2+p3

【2018年湖北省普通高中（全国卷Ⅰ）高考仿真模拟数学理科卷（四）4】我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图5），图6是在“赵爽弦图”的基础上创作出的一个“数学风车”，其中ABCD正方形内部即为“赵爽弦图”，它是由四个全等的直角三角形AFB，BCG，CDH，DAE组成，其中BF=3，AF=4分别延长FA，GB，HC，ED到A′，B′，C′，D′使AA′=FA，BB′=GB，CC′=HC，DD′=ED，连接A′B，B′C，C′D，D′A，我们将图中阴影所在的四个三角形ABA′，三角形BCB′，三角形CDC′，三角形DAD′，称为“风叶”，若在风车内随机取一点，则此点取自“风叶”的概率为（  ）

A. 2449

B. 2549

C. 3964

D. 2564

分析：这三个题目都是典型的将数学美学与三角函数中倍角关系、弧长和面积知识的考查、几何概型中的计算问题（尤其是希波克拉底定理的理解）都能够在渗透数学美学的过程中引导学生体会这些和谐、对称的图形中蕴含的数学思想，以现实生活中朴实的事例结合古典数学为背景考查数学文化相关知识，让学生在深层次理解数学文化并能够在今后的学习和生活中去发现、创造和研究，体会数学来源于生活的本质。

3. 源自与现代科学或生产生活有关系的数学文化背景试题

马克思曾指出，任何一门学科是否成熟，只要看这门学科中数学应用的程度。数学科学在社会科学发展的进程中承担着非常重要的作用。数学文化视角下的试题承担起让学生理解数学与时代进步的紧密關系的重要使命。

【2017～2018年辽宁省沈阳市郊联体高二上期末数学试卷（理科）12】2016年1月14日，国防科工局宣布，嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过，正式开始实施。如图所示，假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行。若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a1a1c2其中正确式子的序号是（  ）

A. ①③

B. ①④

C. ②③

D. ②④

【2018年全国Ⅱ卷理8】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23。在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（  ）

A. 112

B. 114

C. 115

D. 118

分析：弘扬数学文化与现代科学或生产生活有关系素材的试题主要体现为两点：一是挖掘现代科学或生产生活与数学知识的结合点;二是将数学落实到增强数学问题的生活化，使数学的应用贴近学生的生活实际，实现感受“数学来源于生活”的学习理念。

二、 数学文化在教学实践中的教学建议

张奠宙教授曾指出，“数学文化不是处在课堂之外，其必须要进入课堂之中”。数学文化具有比数学知识体系更为丰富的内涵，是对数学知识、能力和数学素养的高度概括。如何在课堂教学活动中，教师通过合理设计教学活动，并在教学过程中渗透数学文化，帮助学生在学习数学知识的过程中形成一种数学文化意识，实现教学内容与数学文化之间的有效结合。

（一） 以数学史为依托，创设情境导入课堂实现数学文化的渗透

数学史是人类文明发展进程中关于数学知识的产生、发展过程的全记录，是高中数学课堂教学活动最为有效的载体。笔者认为教师能够在教学实践活动中对数学史料进行一定的加工，在尊重历史的前提下灵活的用学生喜欢的形式，比如播放数学史的科普视频、数学家简短而又有趣的数学演讲，课堂情境引入数学家的小故事等形式根据教学内容进行合理的选择，在选用的数学史内容时教师一定要紧密联系教学内容，甚至可以将数学史上的内容与现代信息技术结合，增强数学课堂趣味性的同时也能够实现更为有效的数学文化渗透和践行数学源于生活的数学本质，实现数学文化教育的真正目的。

（二） 以数学题材为媒介，结合例题习题实现数学文化渗透

数学文化如何在日常学习过程中高频次的出现？选择部分有趣且极具数学文化特色的数学例题和习题是非常有效的重现形式，既促使课堂内容层次丰富又能够较好地开发学生的从数学问题中形成数学思维的能力。如果教师敢于大胆地为学生提供以著名的数学问题为蓝本开发的数学试题，由学生自己来设计数学问题、改编数学问题的尝试，笔者相信这样的经历一定能让学生对数学文化有更为深入的了解，也能极大的增强学生学习数学的信心。

（三） 通过数学公理，概念和教学本质渗透数学文化，实现数学文化应用于数学实践

在实际的数学课程教学过程中，如果教师只停留在对数学概念和公式的解释上，学生只能被动地接受教师输入的知识、机械的记忆、重复的应用公式、性质和定理，很难达到对数学思维的高度理解，而且谈论学习的热情更加困难。如果教师可以使用数学文化来创造相应的数学问题情境，让学生从数学现象中沿着数学家们的发现探索之路实现学生自我的数学公理、概念、性质的发现和归纳。我想这样的教学设计不但能增强学生学习数学的兴趣，更能激活学生学习数学的主动性。真正让学生感受到数学本身是源自生活实际，并把这种学习精神一直陪伴到今后的學习和生活中去。

三、 结束语

数学文化与教学实践有效的结合，为教学情境的创设、数学思维的形成、学生主体性地位的作用、激发学习兴趣等方面都是总之有效的。然而数学文化本身的综合性非常强，需要我们的教师能够提升对数学文化的认知，从多方面多角度的对数学文化进行了解，加强数学文化的知识储备，在课堂教学活动中通过数学文化的渗透绽放数学之美！

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018：10.

[2]史宁中.数学基本思想18讲[M].北京：北京师范大学出版社，2016：10.

[3]顾沛.数学文化[M].北京：高等教育出版社，2008：6.

[4]伏春玲，冯秀芳，董建德.数学文化在中学数学教学中的渗透[J].数学教育学报，2011，6（20）：89-92.

[5]侯代忠，喻平.彰显数学文化：教学设计中的三个自问[J]数学通报，2018（9）：32-36.