Δ源逆变器的小信号建模与无源器件参数影响分析
(1.山东科技大学 电气与自动化工程学院,山东 青岛 266590;2.哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001)
Z源逆变器的出现在电力电子技术领域具有革命性的意义,目前广泛应用于电机调速系统、分布式电源并网系统、电动汽车等领域。该逆变器直流电源与逆变桥之间由独特的电感电容网络联接,这种网络使得任意一个桥臂直通或者开路都不会对电源和开关器件造成影响。特殊的阻抗网络使得逆变器适用于输入电压或电流有频繁波动的场合,并且在各种功率变换中得到广泛研究与应用,文献[1-3]研究了其在DC/AC电能变换电路中的应用,文献[4-5]将其应用于DC/DC变换电路,文献[6]详细阐述了其在AC/AC电路中的应用。同时一些改进的新型Z源逆变器也被广泛研究[7-17]。
目前对于逆变器的功率等级要求越来越高,传统Z源逆变器的升压性能已经远远达不到应用要求,而且由于逆变器注入直通控制方式使得调制系数与直通占空比存在相互制约关系,一味调高直通占空比会使得调制系数较小,不利于输出波形的优化,输出电压含较多的谐波会加重滤波器的负担,同时开关管承受了较高的电压应力,所以传统的Z源逆变器不适合电压增益较大的场合。另外不连续输入电流、巨大的起动电流等问题制约了Z源逆变器的应用。改进的准Z源逆变器具有连续输入电流,也使得一个电容器的电压应力减小[7-10],但是仍然存在升压能力不足的问题。为了克服这些缺陷,最近几年含耦合电感网络的新型逆变器得到广泛研究,采用耦合电感网络使逆变器可以在较低的直通占空比时仍能获得较高的电压增益,同时减少了电路元件数量,减小了逆变器的体积,具有更为广阔的应用前景。
本研究在以上分析基础上探讨了一种具有新型耦合电感结构的Δ型电抗源逆变器,对该逆变器做出详细的工作原理分析以及耦合电感网络各元件对系统性能的影响分析,并且通过这些性能分析,根据电压电流纹波要求得到电路参数选择的一些规律,并用仿真和实验结果验证了得到的结论。
1 电压型Δ型电抗源逆变器原理分析

图1 AC-DC-AC电能变换Δ型电抗源逆变器电路拓扑Fig.1 Δ-type reactance-source inverter topology applied in AC-DC-AC power conversion
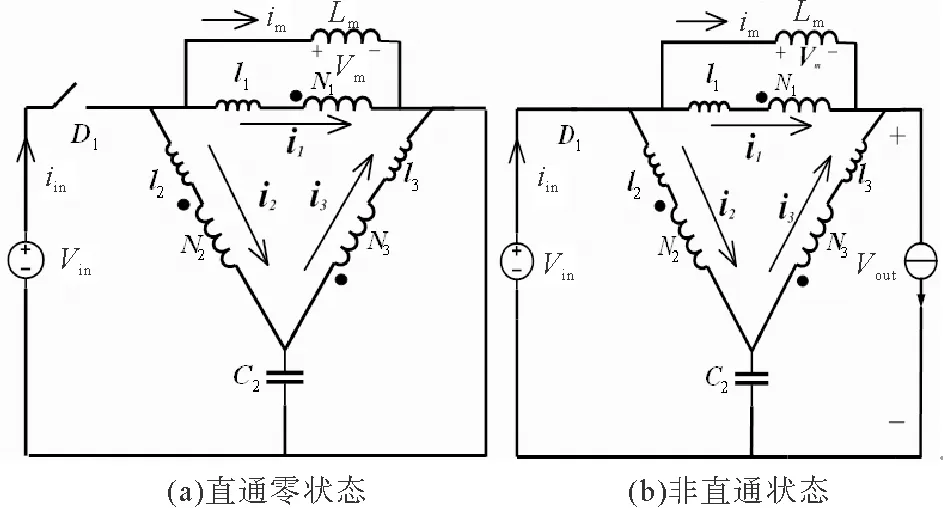
图2 Δ型电抗源逆变器Fig.2 Δ-source inverter
2.1 电路拓扑和工作原理
图1为Δ型耦合电感网络应用于AC-DC-AC电能变换电路的电路结构图。作为直流电源与逆变桥的中间升压级电路,为了便于分析,将Δ型电抗源逆变器简化等效为如图2所示的工作原理图,图中将等效的励磁绕组和漏感也表示出来。由于电路通常带电感性负载或采用LC低通滤波器,因此在图2中将逆变桥用电流源来代替。假定电路工作在理想状态下,耦合电感具有非常高的耦合程度,公式推导时忽略图中漏感和线圈绕组的影响。该逆变器有两个稳定的工作状态:直通零状态和非直通状态。
当逆变器工作在直通零状态时,电源端的二极管D1关断,如图2(a)所示。在这种状态下,电容C2向耦合电感网络充电,各绕组按匝数比的关系分配电压,该过程中第三绕组将流过较大的电流,第一、二绕组流过的电流较小。可得直通零状态下磁化电感上的电压为:
(1)
其中,N1、N2、N3为耦合电感第一、二、三绕组的匝数。
当逆变器工作在非直通状态时,如图2(b)所示,电源端的二极管D1导通,电源和耦合电感网络向负载供电,使输出电压升高。同时电源通过第二绕组向电容充电,此状态第一、二绕组的电流较大,而第三绕组上的电流几乎为零。同样,可以求得非直通状态下磁化电感上的电压:
(2)
从公式(1)和(2)可以计算出电容C2的电压。通过在一个开关周期内对磁化电感上的电压应用伏秒平衡公式可列出:
vmTon+vmToff=0,
(3)
其中,Ton是一个周期T中的直通时间,Toff是非直通时间,考虑到理想三绕组耦合电感的电压与绕组关系,即三个绕组的电压与绕组匝数比相等,再根据绕组之间的基尔霍夫电压定律可得出V1=V2+V3,由此推出绕组匝数的关系:
N1=N2+N3。
(4)
由公式(1)~(4)得电容电压和直流链电压平均值为:
(5)
其中,dst是开关直通占空比。可以很容易地通过计算非直通状态的直流链电压,来获得Δ型耦合电感网络的升压因子G,非直通状态下直流链电压峰值为:
(6)
Δ型耦合电感网络的升压因子G为:
(7)
其中,KΔ是绕组系数,可以得出升压因子与耦合电感网络的KΔ以及dst的大小有关。若逆变电路的调制系数为M,可以推导出三相逆变器交流线电压的峰值为:
(8)
由上面分析可知,Δ型电抗源逆变器有两个可以调整的自由度来实现高电压增益,既可以通过合理改变直通占空比的值,也可以通过改变绕组系数。而对于该类高增益逆变器来说,注入直通零状态的控制方式决定了调制系数与直通占空比存在相互制约关系,这种制约关系从Z源逆变器开始就存在。而Δ型电抗源逆变器的优势就在于可以牺牲直通占空比来保持较大的调制系数,增大绕组系数来保持较高的电压增益,这样既不会影响电压的升压倍数,又使得开关管的电压应力较小。
1.2 相关电路拓扑的升压因子对比
表1给出了三种相关逆变器的参数对比。图3给出了三种逆变器升压能力曲线,可以看出整个曲线是非线性的,Δ型电抗源逆变器的升压能力明显优于级联boost型逆变器和Z源逆变器。图4给出了对应于不同绕组系数KΔ下Δ型电抗源逆变器的升压因子G关于直通占空比dst的关系曲线。由图4可以看出,当选择的绕组系数较大时,直通占空比的一个微小的变化就会导致升压因子的巨大变化;而当选择的绕组系数较小,直通占空比在较小的值变化时,升压因子几乎不变,可以根据实际应用需求合理地选择相关参数。
2 Δ型电抗源逆变器的建模与无源器件参数的影响
2.1 电路的小信号模型
将应用小信号建模法对逆变器进行建模,求出变量的传递函数,分析该新型逆变器的工作性能,包括动态响应、稳定性等。小信号建模法是建立电路模型常用的方法,应用较为广泛。因为电路中存在二极管、开关管等非线性元件,不能采用已有的线性分析理论,但是当时间基准取的无穷小时,这些非线性元件在某些时刻可以当成线性元件来处理,小信号建模法就是利用这一原理。考虑扰动信号作用下的电路运行状态,将Δ型电抗源逆变电路等效为小信号电路。

表1 三种电路拓扑的参数对比Tab.1 Comparison of parameters of three circuit topologies

图3 三种逆变器的升压能力比较Fig.3 Comparison of boosting capability among three types of inverter
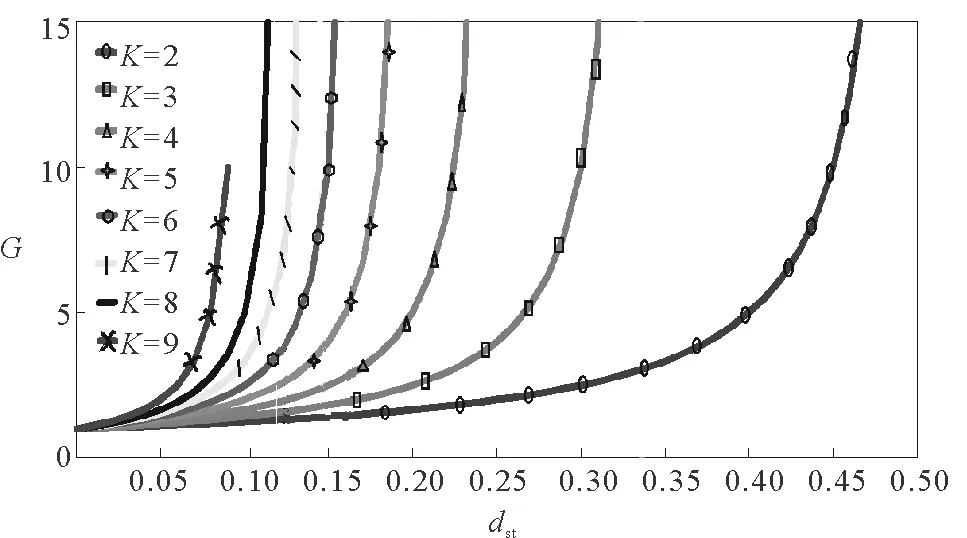
图4 Δ型电抗源逆变器G-dst-K的关系图Fig.4 Relationship of G-dst-K of Δ-source inverter

图5 Δ型电抗源逆变器等效图Fig.5 Δ-source inverter equivalent diagram
Δ型电抗源逆变器的升压过程伴随着电容和电感的充放电,而充放电的快慢直接决定了整个系统的响应速度。推导传递函数时应先建立交流小信号模型,因为Δ型电抗源逆变器适合应用在光伏电源等输入直流电压有波动的场合,因此本研究主要通过交流小信号建模法研究在输入电压有阶跃变化的情况下电路中的电容对电路性能的影响,同时也对直通占空比发生变化时电路参数对系统的影响进行仿真分析。假设电路负载为感性,为了简化分析,将逆变桥等效为一个开关管,电路如图5所示。
图5中瞬时值是由平均值加入扰动值构成的,满足式(5),可以看出扰动值是时变的,所以整个瞬时值也是时变的。
(9)
可以得到
(10)
其中,K是绕组系数,D是直通占空比,K′=N2/N3,D′=1-D,式(10)的等式右侧有三个因子,第一个因子代表了电路的直流小信号模型,第二、三个因子代表了电路的交流小信号模型。电路如图6所示。


图6 电路的小信号模型Fig.6 Small signal model of the circuit
得到输入直流电压到电容电压的传递函数:
(11)
输入直流电压到输出电压的传递函数:
(12)
2.2 不同电容器参数下传递函数的Bode图
下面研究电路电容器对于系统性能的影响。仿真电路的参数如下:N1∶N2∶N3=4∶3∶1,D=0.1,Lm=1 mH,L0=1 mH,R0=10 Ω。取三个数值的电容,分别是680、470、270 μF。将所有数据代入式(11)后,利用仿真软件进行建模仿真,三种电容对应的传递函数的Bode图如图7和8所示。
从仿真结果可以看到系统的相角裕度是大于零的,所以利用Bode图可以证明系统是稳定的。需要注意的是,在受到扰动的时候电容量不同,曲线在中频段的波形是不同的,系统表现的性能也不同。

图7 电容电压-输入电压传递函数的Bode图Fig.7 Bode plot of the transfer function of the capacitor voltage to input voltage

图8 输出电压-输入电压传递函数的Bode图Fig.8 Bode plot of the transfer function of the output voltage to input voltage
一般来说,Bode图的低、中频段能间接地反映系统的性能。在系统的低频段,三条曲线基本重合,而低频段能间接反映系统的稳定性,可以认为电容对系统的稳态性能影响不大。中频段与系统的暂态性能密切相关,观察中频段的波形可以发现,电容量越大曲线越靠下,实际表现为电容量越大对于系统的扰动越敏感。观察三条曲线可以发现,电容量越小,相角裕度略微增大,增加了系统的带宽,使系统的响应速度加快,超调量减小,系统更加稳定。

图9 电容电压-输入电压传递函数的零极点图Fig.9 Zero-pole plot of the transfer function of the capacitor voltage to input voltage
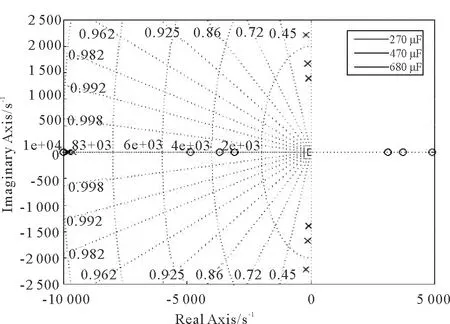
图10 输出电压-输入电压传递函数的零极点图Fig.10 Zero-pole plot of the transfer function of the output voltage to input voltage
由零极点图9和10可以发现,随着电容值的增大,两个图形中极点都沿着虚轴向坐标原点靠近。较大的电容将会降低系统的阻尼,经过较长时间才能达到新的稳定状态,并且会出现超调和振荡现象,与Bode图得出的结论基本一致。
2.3 无源元件参数对电路性能影响的仿真分析
上述两个传递函数,都是电源电压作为输入量,由于直通占空比作为输入量的传递函数的推导比较复杂且计算量很大,通过仿真来进行讨论。另外,电感对于系统性能的影响也将在本节通过仿真研究。
外界的扰动主要考虑输入直流电压的跃变以及直通占空比的跃变,考虑这两种扰动都具有实际意义。若是将Δ型电抗源逆变器应用于光伏发电系统,则前者可以模拟实际系统中太阳能电池所产生的直流电压的波动,后者则可以模拟受到外界因素影响使得某一桥臂发生直通扰动的情况。
首先,保持电路中耦合电感网络的匝数比不变,仿真中设定耦合电感的匝数比为60∶45∶15,运用Matlab/Simulink进行仿真,研究电容对于电路性能的影响。仿真结果如图11和12所示,可以看出电容量越大,输入直流电压或直通占空比发生阶跃变化时,输出电压振荡越明显,同时调整时间也越长,验证了前面小信号建模法得出结论的正确性。因此,在电路升压倍数满足要求和电路正常工作的情况下,尽量取较小的电容值来改善电路的动态性能,但是也需要考虑使电容电压纹波满足系统的要求。
其次,保持电容量不变,分析耦合电感网络的电感对系统的影响。
耦合电感网络是Δ型电抗源逆变器用于升压的核心部分,其正常运行对逆变器起着至关重要的作用。每匝线圈的电感值与匝数、磁芯形状和材料都有关系。本研究中开关频率较高,因此选择性能优良的锰锌铁氧体作为磁芯材料,一般磁导率在几百到三万之间,线圈匝数与电感满足下列关系:
(13)
(14)

图11 输入电压变化时电容对电路性能的影响Fig.11 Effect of capacitance on circuit performance during change in input voltage
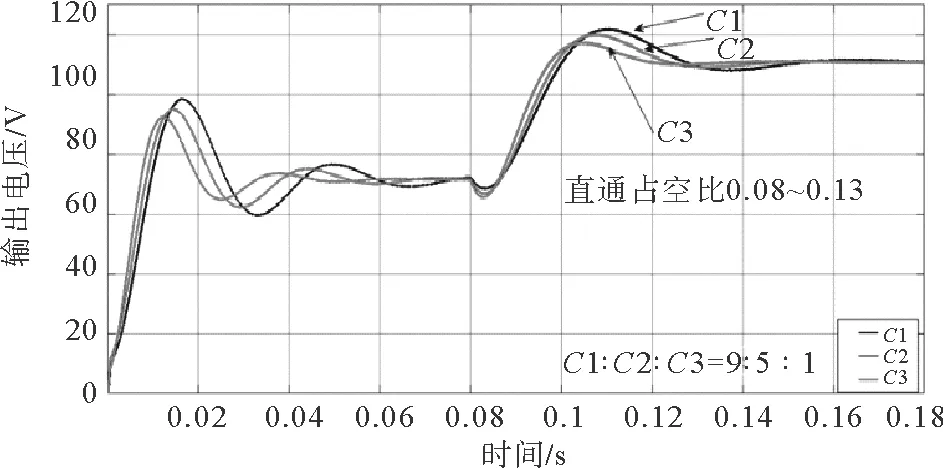
图12 直通占空比变化时电容对电路性能的影响Fig.12 Effect of capacitance on circuit performance during change in shoot-through duty ratio
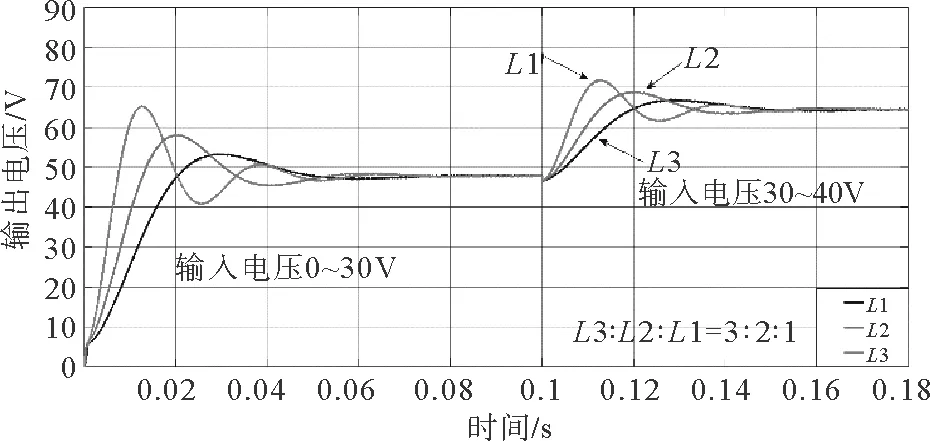
图13 输入电压变化时耦合电感网络电感对电路性能的影响Fig.13 Effect of coupled inductor on circuit performance during change in input voltage
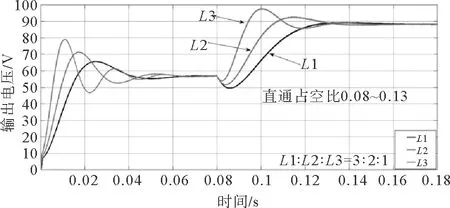
图14 直通占空比变化时耦合电感网络电感对电路性能的影响Fig.14 Effect of coupled inductor on circuit performance during chnge in shoot-through duty

表2 系统参数Tab.2 System parameters
在磁芯材料不变的情况下,耦合电感匝数越多,电感值越大,能够为电路提供更加充沛的电能。电感一方面具有减缓启动电流的作用,但另一方面又会使电路动态响应迟缓。在不考虑线圈漏感的情况下,通过三组电感值的仿真对比,可以发现电感的值越大,系统的最大超调量越小。大电感适合稳定的电压输出,但随着电感值变大,系统的调整时间同时会变得比较长,表现为系统电压响应比较慢。由此可见,大电感可以使系统响应过程变得平缓,代价是延长系统的响应时间,所以在电感电流纹波满足系统要求的前提下,要根据不同的负载需求来合理选择电感的数值。大电感适合于要求稳定输出的负载,小电感适合于要求响应速度较快的负载,所以要合理选择电感参数使得系统工作状态最佳。另外在直通占空比变化的情况下,可以看到突变点附近波形会先向下运行一段时间,这种现象造成的原因是直通占空比-输出电压的传递函数存在一个位于虚轴右侧的零点,导致这个系统变成了非最小相位系统。
3 样机实验与结果分析
根据电路原理图搭建样机模型,采用普通SPWM控制产生功率管直通信号,实验电路如图15所示,系统参数如表2所示,SPWM控制信号生成的仿真模型如图16所示,输出波形如图17所示。当绕组系数等于3,直通占空比为0.1时,开关管电压应力(直流链电压)等于14.3 V,与理论推导结果一致。图18给出了Δ源逆变器的效率,其大小受开关损耗和绕组损耗的影响较大。通过示波器测出的实验波形如图19(a)~(e)所示,其中输出线电压峰值和电容器电压应力与由式(5)和式(8)计算的理论值稍有误差,这是因为在搭建电路模型时,受到漏感和线圈电阻的影响,不可能做到电感的全耦合。从图19(d)~(e)分析可知,当从非直通状态向直通状态变换时,二极管两端将出现电压过冲和震荡,但幅值不大,对电路产生的影响较小。同样,当直通状态向非直通状态转换时,开关管两端也会出现电压过冲和震荡,但经过很短的过渡时间就趋于稳定。

图15 Δ型电抗源逆变器实物图与实验图Fig.15 Prototype of experimental circuit
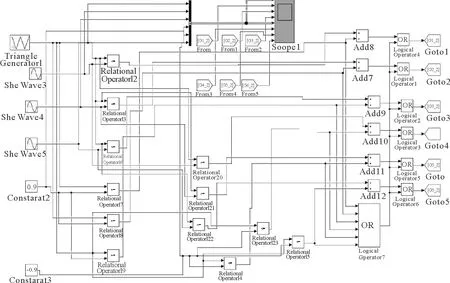
图16 SPWM控制信号生成仿真图Fig.16 Simulation diagram of SPWM control signal generation
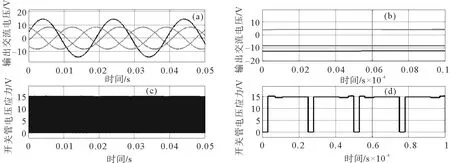
图17 输出波形M=0.9,D=0.1Fig.17 Output waveform at M=0.9,D=0.1
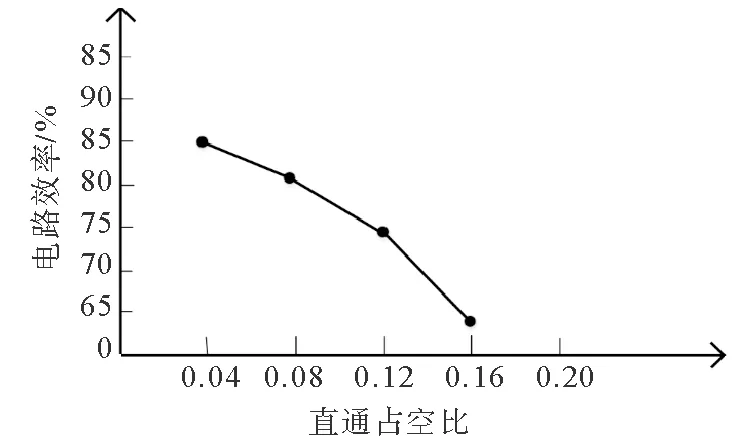
图18 Δ型电抗源逆变器电路效率Fig.18 The efficiency of the Δ-source inverter
逆变器的工作效率定义为输出功率/输入功率。由图18可以看出电路的效率将随着直通占空比的提高而降低,造成这种情况的原因主要是直通电流过大造成了绕组损耗以及开关损耗增大,可以通过选择性能优良的线圈绕线和电路器件来减小电路损耗。

图19 实验结果Fig.19 Experimental results
4 结论
本研究在对新型Δ型电抗源逆变器进行详细的工作原理分析的基础上,得到电路的电压增益关系。通过小信号建模法建立了系统的数学模型并求出相应的传递函数,画出Bode图和零极点图,通过波形对比分析各无源元件对系统性能的影响,得到电路参数选择的一些规律。Δ型电抗源逆变器除了继承Z源逆变器的全部优点之外,还具有以下优势:
1)通过独特的三角形状的耦合电感结构,可以实现灵活的升降压功能,线圈电感的电流抑制作用使得启动电流的影响很小。
2)能够在较大的直通占空比下保持较小的开关电压应力,同时也能够在较小的直通占空比下仍保持较高的电压增益。
3)具有较低的绕组损耗和绕组电压降。Δ型电抗源逆变器具有更高的电路效率,较小的体积与重量。
但由于耦合电感不可避免的存在漏感,而漏感的存在对电路的工作过程会造成一定的影响,需要采取措施消除漏感的影响。因此,Δ型电抗源逆变器主要适用于要求电压增益较高的应用场合,而Z源电路主要适用于电压增益要求不是太高的应用场合。

