空旷环境下小药量集中药包爆炸冲击波衰减规律

王海亮1，张琪帆1，王有权，刘 鹏

(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266590；2.中铁三局集团有限公司，山东 青岛 266000)

随着城市建设的迅猛发展，位于城市繁华地段或人员密集区域的露天爆破安全越来越多地引起关注和重视。虽然露天爆破起爆药量较小，但如果控制不当，爆破产生的空气冲击波也会对临近建筑物产生破坏、对周围人员产生生理和心理上的伤害或不利影响。因此，开展空旷环境下小药量冲击波传播及衰减规律的研究具有重要意义。

岳军政等[1]通过研究含铝炸药在空气中爆炸形成的初始冲击波，推导出含铝炸药等非理想炸药的冲击波超压理论计算方法。曲志明等[2]基于欧拉坐标系建立模型推导出瓦斯爆炸冲击波超压的衰减公式。许大鹏等[3]指出了大型爆破常用的危险半径及地震波震速计算公式中主要系数存在的问题并提出了解决方法。李富国[4]、唐海等[5]针对目前城市控制爆破工程中的爆破事故以及爆破危害产生的原因,结合实践经验,提出了相应的控制措施以及降低危害的具体办法。陈士海等[6]运用LS-DYNA软件,模拟了二层两跨典型砌体结构在不同爆破地震波作用下的动力响应,发现地震波幅值的增加可明显加剧结构损伤。夏曼曼等[7]对乳化炸药空中爆炸冲击波衰减规律进行了研究，对已有的经验公式进行修正，得到乳化炸药空中爆炸冲击波衰减公式。遗憾的是，文献中试验选取的比例距离大多小于10，对于比例距离大于10的情况，缺乏试验数据的验证。

本研究利用冲击波传感器及信号分析仪测试了2号岩石乳化炸药在露天空旷环境下爆炸时，爆心距为2～16 m，炸药量为0.1、0.2和0.3 kg情况下的冲击波超压峰值，得到露天空旷环境下爆炸冲击波超压峰值的衰减规律，对空旷环境下冲击波超压峰值的计算公式进行修正，对控制城区露天爆破冲击波危害以及研究爆炸冲击波的传播衰减规律具有一定的参考价值。

1 集中药包空旷环境爆炸试验

1.1 试验场地

试验于2018年9月13日、14日进行，试验地点选在青岛地铁13号线海洋大学站附近一个较为空旷的区域，地势较为平坦。

1.2 试验方案

分别选取0.1、0.2和0.3 kg的2号岩石乳化炸药作为试验用炸药，炸药长度与截面直径比为14～17，因此可以视为集中药包[8]。药包布置于高1.4 m的炸药支架上，使用导爆管雷管按单个药包分次起爆。冲击波测试使用NUBOX-9100冲击波信号分析仪及配套冲击波传感器。该信号分析仪每台有2个通道，可连接2个冲击波传感器。现场共设置2台冲击波信号分析仪，搭配4个冲击波传感器，分别放置于距爆源一定距离4个测点的传感器支架上，传感器支架高1.4 m，与炸药处于同一水平高度。图1为试验现场测点布置示意图。

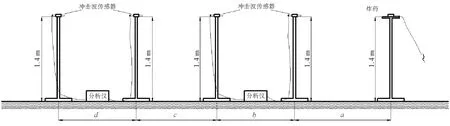
图1 试验现场测点布置示意图Fig.1 Schematic diagram of measuring point arrangement in test site

图中a代表距爆源最近处的传感器与爆源之间的距离，b、c、d代表各传感器之间的距离。a、b、c、d的取值根据现场试验要求进行调整。

1.3 试验数据

本次试验共进行0.1 kg起爆药量1次、0.2 kg起爆药量3次、0.3 kg起爆药量4次。表1是试验得到的8组爆心距与超压峰值数据的汇总表。

表1 空旷环境不同起爆药量下爆炸冲击波超压值Tab.1 Shock wave overpressure value of explosive explosion test in open area kPa

2 试验结果分析

自1955年以来，有众多国内外的专家学者对冲击波超压衰减规律进行了研究，并得出相关公式，其中的典型代表有：Brode经验公式、Henrych经验公式、Mills经验公式和Sadovskyi经验公式。本研究结合试验结果与经验公式进行分析，试图得到更适合小药量条件下的冲击波超压计算公式。

2.1 冲击波超压经验公式

Brode[9]在1955年提出的关于高爆炸药冲击波超压峰值的经验公式为：

(1)

Henrych[10]在1979年对空气中冲击波的超压峰值进行了推导，得到表达式：

(2)

Mills[11]使用数值模拟和相似理论结合的方式，求得了TNT爆炸产生的冲击波超压峰值经验公式：

(3)

Sadovskyi[12]依据模型相似性理论建立了比例距离关系的比较式，根据试验确定系数，得到高爆炸药冲击波超压峰值的经验公式：

(4)

2.2 经验公式与试验结果对比分析

将试验所用到的炸药量与爆心距进行计算，得到比例距离z，再将z值代入4个经验公式得到经验公式超压计算值。由于数据较多，为了更加直观地分析上述经验公式的计算值与本次现场试验超压峰值的区别，分别绘制出不同爆心距处0.2 kg炸药和0.3 kg炸药的超压峰值，如图2和图3所示。图中曲线B、H、M、S分别为Brode经验公式、Henrych经验公式、Mills经验公式和Sadovskyi经验公式所对应的曲线。

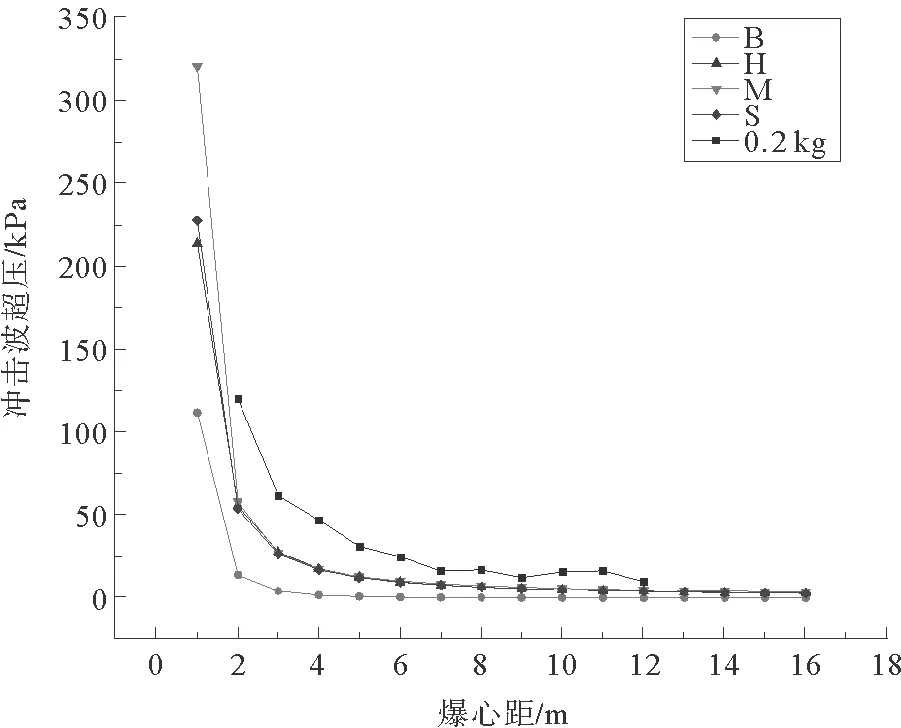
图2 经验公式和实测超压峰值与爆心距的关系(WT=0.2 kg)Fig.2 Relationship between empirical formula and measured peak value of overpressure and detonation center distance (WT=0.2 kg)

图3 经验公式和实测超压峰值与爆心距的关系(WT=0.3 kg)Fig.3 Relationship between empirical formula and measured peak value of overpressure and detonation center distance (WT=0.3 kg)

试验测得的超压峰值在3 m内随爆心距的衰减趋势与Brode、Henrych、Sadovskyi经验公式的计算结果一致，而Mills经验公式在3 m内冲击波超压峰值衰减趋势与其他经验公式以及试验值均不同。Mills经验公式未对z值进行定义域划分，导致该公式在爆心距小于3 m时存在较大偏差。爆心距大于3 m后，试验值与4个经验公式计算值冲击波超压峰值衰减趋势均一致。但在数值上，试验值整体要远高于4个经验公式的计算值。由于经验公式对于z的取值范围较小，因此Brode、Henrych、Sadovskyi及Mills经验公式并不适合z>10条件下的计算。

试验中每台分析仪连接2个传感器，当冲击波传播至第一个传感器时，信号分析仪开始记录时间，因此可以通过冲击波超压产生的时间差和两个传感器之间的距离计算出平均速度。从图4可见，冲击波的传播速度在爆心距12 m处已衰减为爆心距2 m处冲击波传播速度的60%。

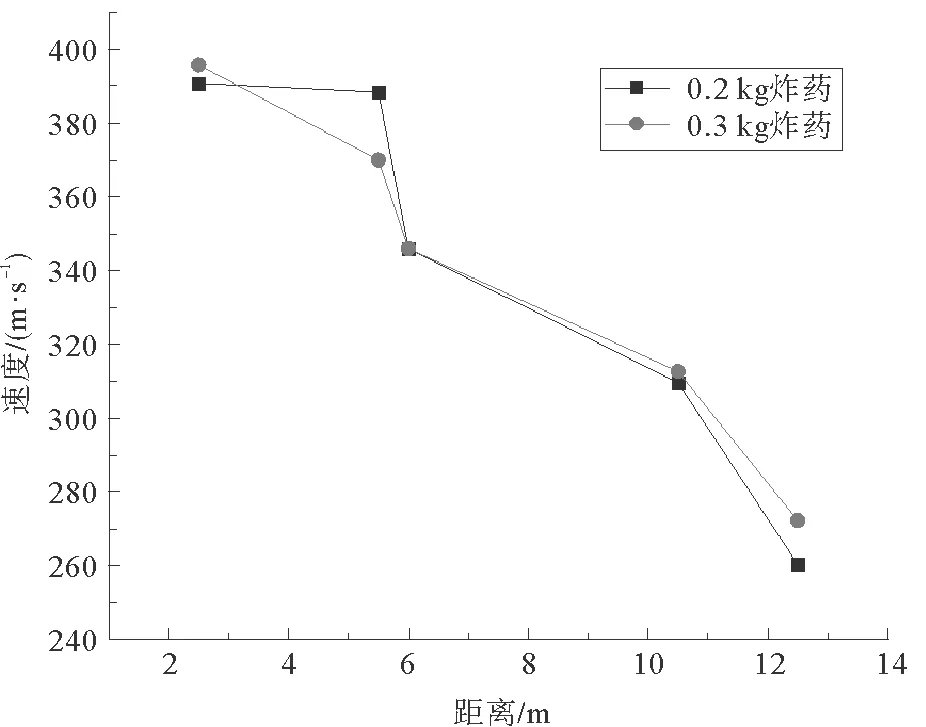
图4 冲击波传播速度随距离的衰减趋势Fig.4 Attenuation trend of shock wave propagation velocity with distance

2.3 小药量集中药包冲击波超压峰值计算公式

通过经验公式与试验数据的对比，应用爆炸相似率原理，对经验公式进行修正。通过最小二乘法原理将表1中的数据拟合，得到了小药量集中药包冲击波超压峰值计算公式(5)。为了便于讨论，将此计算公式简称为XiaoYL公式。

(5)

同时将0.2 kg、0.3 kg药量的试验值、XiaoYL公式与Brode、Henrych、Mills、Sadovskyi经验公式计算所得冲击波超压峰值与爆心距的关系作曲线图进行分析，如图5和图6。

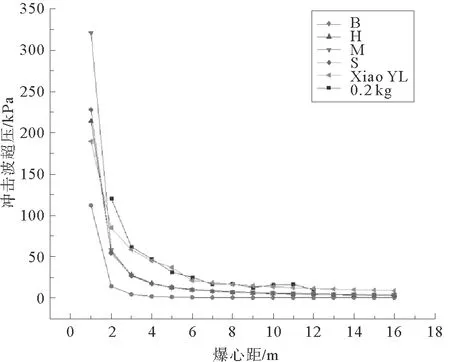
图5 冲击波超压与爆心距的关系(WT=0.2 kg)Fig.5 Relationship between shock wave overpressure and detonation center distance (WT=0.2 kg)

图6 冲击波超压与爆心距的关系(WT=0.3 kg)Fig.6 Relationship between shock wave overpressure and detonation center distance (WT=0.3 kg)

从图5～6可以看到，XiaoYL公式冲击波超压峰值随爆心距衰减速率与试验值一致。当爆心距在1～3 m时，冲击波超压峰值的衰减速率约为75.61 kPa/m；爆心距3～8 m时衰减速率降低到10.12 kPa/m；当爆心距大于8 m时，衰减速率趋于平缓，约为0.48 kPa/m。XiaoYL公式计算所得冲击波超压峰值与现场试验值基本相同。爆心距小于4 m时，XiaoYL公式计算所得冲击波超压峰值略小于试验值，约为试验值的85%。而在爆心距大于4 m后，冲击波超压峰值衰减速率趋于平稳时，XiaoYL公式计算所得冲击波超压峰值与试验值吻合。由于比例距离与爆心距、炸药量有关，因此为了分析XiaoYL公式的准确性，对Brode、Henrych、Mills、Sadovskyi经验公式、XiaoYL公式以及试验值作爆心距为3 m和8 m时冲击波超压峰值与炸药量的关系图，如图7和图8所示。

从图7和图8可以看到，在爆心距为3 m和8 m时，Henrych、Mills、Sadovskyi经验公式冲击波超压峰值随炸药量变化值小于试验值，约为试验值的40%～50%，而Brode经验公式的偏差更大，仅为试验值的10%左右。这与Brode经验公式在比例距离z>1时的方程形式有关，原因是其方程形式与Henrych、Mills、Sadovskyi经验公式不一致，导致了偏差较大的情况。

图7 XiaoYL公式与经验公式冲击波超压和炸药量关系(3 m)Fig.7 Relationship between XiaoYL formula and empirical formula shock wave overpressure and explosive quantity (3 m)

图8 XiaoYL公式与经验公式冲击波超压和炸药量关系(8 m)Fig.8 Relationship between XiaoYL formula and empirical formula shock wave overpressure and explosive quantity (8 m)

图9 经验公式、XiaoYL公式与试验数据的相对误差Fig.9 Relative errors between empirical formula,XiaoYL formula and test data

经过对经验公式的修正，XiaoYL公式冲击波超压峰值随炸药量变化值与试验值基本一致。为了更加准确地分析XiaoYL公式、Brode、Henrych、Mills、Sadovskyi经验公式相对于试验值的误差，作图9。

由图9可见，Henrych、Mills、Sadovskyi经验公式对于试验值的相对误差分别为0.82、0.63、0.62，Brode经验公式更是达到了0.95以上，而XiaoYL公式对于试验值的相对误差则为0.11。由此可见，XiaoYL公式冲击波超压峰值与现场实际情况更为接近，能更准确地为施工现场提供依据。

3 数值模拟

为了验证XiaoYL公式的准确性，运用ANSYS/LS-Dyna建立试验模型并进行分析。

3.1 ANSYS模型建立

根据现场试验运用ANSYS R18.1，建立截面为4 m×4 m、长20 m的长方体空气模型，模型涉及炸药、空气2种材料，计算时采用ALE多物质耦合方法，使2种物质可共存于一个网格内。

炸药依据竖井爆破常用的2号岩石乳化炸药选取材料参数，选用HIGH_EXPLOSIVE_BURN模型，通过JWL状态方程(式(1))描述爆炸时的压力和体积膨胀关系。C-J压力取3.72 Gpa，炸药密度、爆速及状态方程中的参数见表2。

(6)

式中：P为炸药爆轰压力；V为炸药爆轰产物相对比容，E0为炸药初始比内能；A、B、R1、R2、ω为状态方程的参数。

表2 炸药计算参数Tab.2 Calculation parameters of explosives

空气采用NULL材料模型，状态方程使用*EOS_LINEAR_POLYNOMIAL线性多项式，形式为：

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E。

(7)

式中：P为爆轰压力；C0～C6为状态方程参数，取C0=C1=C2=C3=C6=0，C4=C5=γ-1；μ=ρ/ρ0-1。ρ、ρ0及γ分别为气体的初始密度、密度、绝热指数。模型参数取值：ρ0=1.29×10-3g/cm3，γ=1.4。E为初始单位体积内能，取E=2.5×105J。

3.2 数值模拟计算结果分析

使用Lsprepost 4.3对模型计算结果进行分析。取模型中线上的点如图10所示，提取对应距离上冲击波超压峰值，所取测点处超压峰值见表3。

图10 数值模拟模型Fig.10 Analysis diagram of analog model

对模型测点所得超压峰值与试验值、XiaoYL公式进行对比，得到如图11所示的曲线图。

表3 数值模拟测点处超压峰值Tab.3 Numerical simulation of point overpressure peak

图11 模拟计算值与XiaoYL公式超压值对比Fig.11 Comparisons between simulated values and overpressure values of XiaoYL formula

通过图11可以看出，模拟计算值与试验超压值、XiaoYL公式计算值十分接近，说明使用XiaoYL公式计算空旷环境下小药量集中药包的爆炸冲击波超压值具有较高的可靠性。

4 结论

利用冲击波传感器与信号分析仪对2号岩石乳化炸药集中药包在露天空旷环境下进行试验，分析爆炸产生的冲击波超压值与爆心距、药量的关系，得到如下结论。

1)计算2号岩石乳化炸药小药量集中药包爆炸冲击波超压峰值的XiaoYL公式为：

2)小药量集中药包爆炸冲击波在空旷环境下传播速度随爆心距衰减较快，在爆心距12 m处衰减为爆心距2 m处冲击波传播速度的60%。

3)当爆心距在1～3 m时，冲击波超压峰值的衰减速率约为75.61 kPa/m；爆心距在3～8 m时衰减速率降低到10.12 kPa/m；当爆心距大于8 m时，衰减速率趋于平缓，约为0.48 kPa/m。