基于绝对吸附量的页岩吸附CH4和CO2的热力学特征
薛 培,祁攀文,杨添麒1,孙德瑞,张丽霞,高栋臣
(1.陕西延长石油(集团)有限责任公司研究院,陕西 西安 710075;2.陕西省页岩气勘探开发工程技术研究中心 陕西 西安 710075)
页岩气是可实现经济规模勘探开发、资源丰富的非常规天然气,主要以游离态和吸附态赋存于页岩孔裂隙和黏土矿物颗粒及有机质孔隙的表面,其中吸附气占总气量的20%~85%[1],在页岩气储量中占有重要地位。页岩气的吸附过程往往伴随着热力学能的变化,并以吸附热的形式体现出来。吸附热反映了吸附剂对吸附质吸附作用力的强弱,可用来判断吸附作用的类型,分析吸附剂表面的不均匀性。因此,研究页岩吸附过程的热力学特性,能够进一步明确页岩气的吸附机理。
目前针对海相页岩和煤岩的热力学研究成果较多,少有针对陆相页岩的热力学研究。川南龙马溪组页岩[2]吸附过程的等量吸附热大于解吸过程,等量吸附热与吸附量满足线性正相关关系;四川盆地牛蹄塘组页岩[3]、柴达木盆地石炭系页岩[4]等量吸附热随吸附量增加而降低;煤岩的吸附热力学分析表明,随着煤级的提高等量吸附热增加,煤岩等量吸附热与吸附量满足线性关系[5];Nodzenski等[6]根据煤岩吸附CH4、CO2的等温吸附实验,发现煤岩对CO2吸附热大于对CH4的吸附热;Kim等[7]研究了亚临界状态至超临界条件下煤岩对CH4和CO2的吸附特征,从热力学角度揭示了煤体表面竞争吸附的本质。可见不同吸附剂-吸附质体系的热力学特征存在明显差异。现有研究成果均采用等温吸附实验直接测得的吸附量即过剩吸附量作为热力学分析的基础数据,而过剩吸附量不能表征吸附剂的实际吸附量(绝对吸附量),基于过剩吸附量计算获得的等量吸附热不能真实反映吸附过程的热力学特征。本研究选取鄂尔多斯盆地甘泉地区延长组页岩,开展30、45及60 ℃页岩吸附CH4和CO2的等温吸附实验,对页岩吸附不同气体的过剩吸附量与绝对吸附量间的差异进行研究,对比分析基于过剩吸附量和绝对吸附量的延长组页岩吸附CH4和CO2的等量吸附热特征。研究成果对完善吸附热力学的分析方法,进一步明确陆相页岩CH4和CO2的竞争吸附机理具有重要意义。
图1 采样位置示意图Fig.1 Location map of sampling sites
1 地质概况
鄂尔多斯盆地地处华北克拉通西部,为大型多旋回叠合盆地。盆地区域构造简单,断裂不发育,总体为西倾的斜坡构造,经历了由古生代海相沉积到中生代内陆湖盆沉积的发展过程。
晚三叠世是盆地湖泊发育的鼎盛时期,暖湿气候及湖泊沉积环境为页岩气的形成提供了良好的基础条件。晚三叠世长7时期,沉积中心位于盆地中南部地区,主要发育半深湖—深湖沉积微相,沉积形成长7段暗色页岩(张家滩页岩),厚度约400~500 m,其中单层厚度达30 m,甘泉地区长7段页岩厚度45~60 m。
2 实验
2.1 实验样品
实验样品来自鄂尔多斯盆地甘泉地区下寺湾镇CY1井的页岩,取样深度为1 024 m,取样层位为上三叠统延长组,具体取样位置见图1所示。所用样品为灰黑色页岩,比表面积为3.54 m2/g,TOC为4.31%,有机质类型以II1型为主,Rran为0.91%,石英含量14.4%,长石含量10.5%,黏土矿物含量53.7%,含少量黄铁矿和碳酸盐等。
由于延长组页岩有机质演化程度较低,热演化过程中形成的大量液态烃占据了页岩中的微孔隙,且甲烷易溶于液态烃,因此为消除液态烃对样品吸附性能的影响,需对页岩样进行有机质溶剂抽提。实验样品来自同一块岩心样,经室内抽提、真空干燥、破碎、筛选,制成粒度约0.2 mm的碎样,并根据实验需求分为3份,密封备用。
2.2 实验方法
本次实验所用仪器为FY-KT 1000型等温吸附仪,实验方法参照GB/T 19560—2008《煤的高压等温吸附试验方法》的相关规定。根据取样地层温度、压力条件,设定实验温度分别为30、45、60 ℃三个温度点,实验初始压力为0.5 MPa,压力上限为16 MPa,不同温度下的压力段内共测定10~11个压力点,测试由初始压力逐渐增加到压力上限,每个平衡压力点下的平衡时间不小于12 h。实验气体分别为纯度99.99%的CH4和CO2。
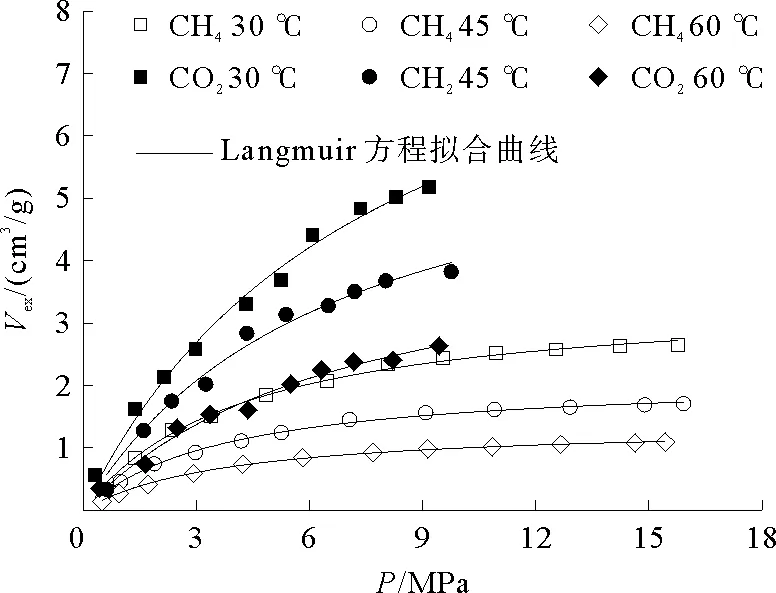
图2 延长组页岩等温吸附曲线Fig.2 The sorption isotherm of shale of Yanchang formation

表1 等温吸附曲线的Langmuir方程拟合参数Tab.1 The fitting parameters of Langmuir equation
注:下标ex表示过剩吸附量,与下文中的绝对吸附量下标ab区分
3 实验结果与分析
本次实验样品来自同一块岩心样,且样品制备方法及样品规格相同,但实验温压条件及吸附质类型不同,实验结果存在差异。根据压力、CH4和CO2吸附量等测试数据绘制等温吸附曲线如图2所示。
由图2可知,相同温压条件下,延长组页岩对CO2的吸附性能大于对CH4的吸附性能。随着温度的升高,页岩的吸附能力下降。
采用Langmuir方程对等温吸附曲线进行拟合,Langmuir方程可表示为
(1)
其中:V为等温吸附量,g/cm3;VL为Langmuir体积,代表最大吸附量,cm3/g;PL为Langmuir压力,代表吸附量达到最大吸附量一半时的压力,Pa;P为压力,Pa。Langmuir方程拟合结果见表1。
Langmuir方程在煤层气、页岩气的等温吸附曲线拟合中应用较为广泛,其假设吸附质分子之间不存在相互作用,吸附剂表面具均质性,适用于描述均匀固体表面的单分子层吸附过程,在低气体压力(≤15 MPa)阶段具有较高的拟合精度。由表1可以看出,随着温度的升高,Langmuir体积(VL)逐渐降低,Langmuir压力(PL)与温度关系不明显。
采用线性函数对Langmuir体积与温度关系进行拟合,结果如图3所示。Langmuir体积与温度呈线性负相关关系,且页岩吸附CO2的Langmuir体积比CH4更具温度敏感性。并且泥页岩Langmuir体积与孔隙度、有机质丰度、有机质成熟度、黏土矿物质量分数均呈正相关关系,与平均孔径呈负相关关系。
由于CH4、CO2的临界温度分别为-82.6、31 ℃,临界压力分别为4.64和7.4 MPa,所以当实验温压条件超过气体临界条件后,气体在页岩中的吸附为超临界吸附。超临界状态下的等温吸附曲线存在极大值,但研究区实验结果并未出现极大值。类似情况如刘圣鑫等[8]在测定柴达木盆地石炭系页岩吸附CO2时出现极大值,但吸附CH4未出现极大值,说明极大值的出现与气体类型有关;另外,周理等[9]认为实验压力及比表面积足够大条件下才可能出现极大值。
4 绝对吸附量与过剩吸附量
等温吸附实验获得的吸附量为过剩吸附量,是实际吸附气密度减去气相密度剩余部分对应的吸附量,而绝对吸附量是吸附过程的实际吸附量。目前多采用Moffat和Weale[10]提出的公式实现由过剩吸附量向绝对吸附量的转换,该公式为:
(2)
其中:Vab为绝对吸附量,g/cm3;Vex为过剩吸附量,g/cm3;ρg为吸附平衡条件下的气相密度,g/cm3;ρa为吸附相密度,g/cm3。
4.1 气相密度计算方法
由于实验温压条件下CH4和CO2压缩因子的变化幅度较大(图4),若采用理想气体状态方程计算气相密度会造成较大误差,因此需采用真实气体状态方程计算气相密度,气相密度可表示为:
(3)
其中:M为摩尔质量,g/mol;Z为真实气体压缩因子,由Peng-Robinson方程计算得到;R为通用气体常数,8.314 J/(K·mol);T为绝对温度,K。
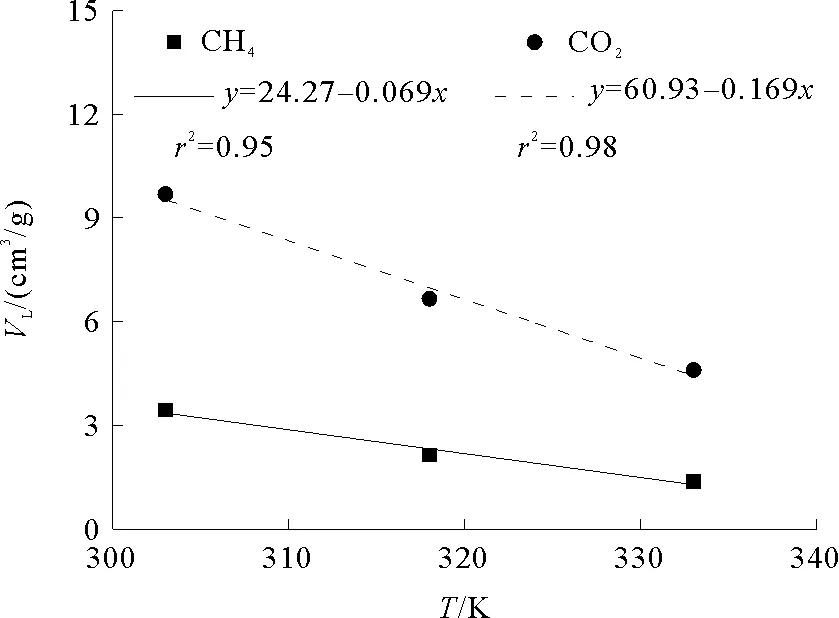
图3 Langmuir体积与温度的关系Fig.3 The relationship between Langmuir volume and temperature
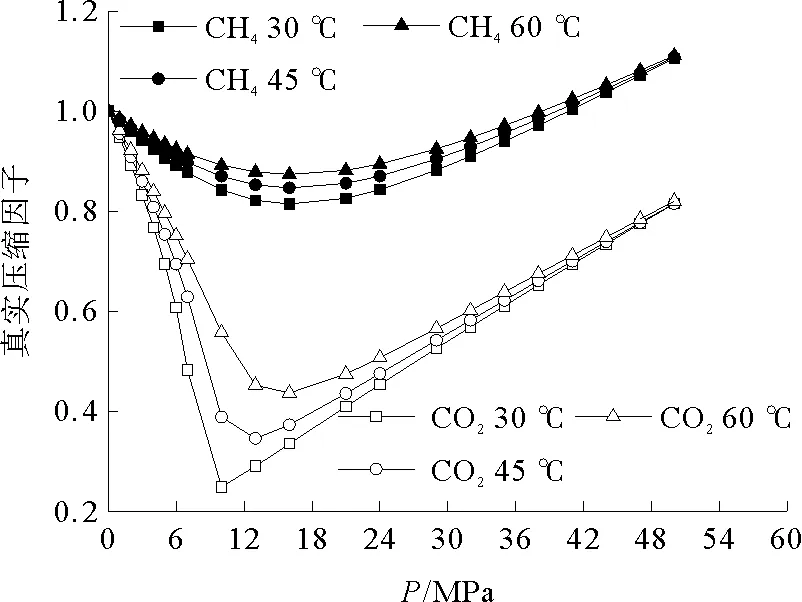
图4 CH4及CO2压缩因子变化曲线Fig.4 The compressibility factor of CH4 and CO2
实验温压条件下CH4和CO2的相态变化及密度曲线如图5所示。由图5(a)可以看出对于CH4而言,实验条件下存在由气相向超临界状态的相态变化。由图5(b)可以看出,对于CO2而言,实验温度30 ℃低于其临界温度(31 ℃),此温度下CO2由气相向液相转变;实验温度45、60 ℃下,CO2由气相向超临界状态转变;CO2相变过程中,密度大幅增加。
4.2 吸附相密度计算方法
目前吸附相密度无法直接测定,多采用理论近似法和经验公式法计算[11]。常用的吸附相密度计算方法如表2所示。其中:M为摩尔质量,g/mol;R为通用气体常数,8.314 J/(mol·k);Tc为临界温度,K;Pc为临界压力,Pa;ρlp为常压沸点液相密度,g/cm3;ρc为临界密度,g/cm3;Tb为沸点温度,K;α为过热液体的热膨胀系数。
超临界条件下吸附相密度明显大于临界密度,低于常压沸点液体密度。选用经验公式法计算吸附相密度,其中:对于CH4,α取0.001 6;对于CO2,α取0.001 5。
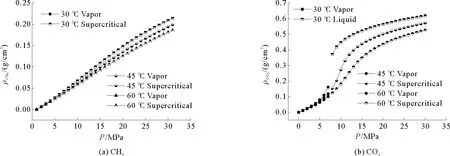
图5 CH4和CO2的相态变化及密度曲线Fig.5 The phase change and density curve of CH4 and CO2

表2 吸附相密度计算方法Tab.2 The calculation method of adsorbed phase density
4.3 绝对吸附量计算
基于等温吸附实验结果,利用公式(2)结合气相密度和吸附相密度的计算方法,将过剩吸附量转换为绝对吸附量,绝对吸附量拟合曲线如图6所示。通过绝对吸附量与过剩吸附量对比(图2)分析可知,绝对吸附量大于过剩吸附量,二者差值受温压条件及气体类型等因素影响。在低压力阶段(0~4 MPa)二者差值较小,随着压力的增加,差值逐渐增加;低温条件下,二者差值较高温条件下大;页岩吸附CO2的绝对吸附量与过剩吸附量差值大于同温压条件下页岩吸附CH4。

注:实线为Langmuir方程拟合线,虚线代表Frenudlich方程拟合线图6 延长组页岩吸附不同气体的绝对吸附量曲线Fig.6 The absolute adsorption isotherm of shale of Yanchang formation
采用Langmuir方程式(1)和Freundlich方程对绝对吸附量曲线进行拟合。Freundlich方程可表示为:
V=kP1/n。
(4)
其中k、n为拟合常数。方程拟合结果及拟合参数如图6、表3所示。以相关系数r2作为标准,拟合结果表明:在临界温度以上Langmuir方程对绝对吸附量曲线的拟合效果较Freundlich方程更好;对于30 ℃页岩吸附CO2的过程,该实验温度位于CO2的临界温度以下,吸附过程中存在着CO2由气相向液相的转变,Langmuir方程的拟合参数Langmuir体积与Langmuir压力明显不具有现实意义,曲线的Freundlich方程的拟合度更高。
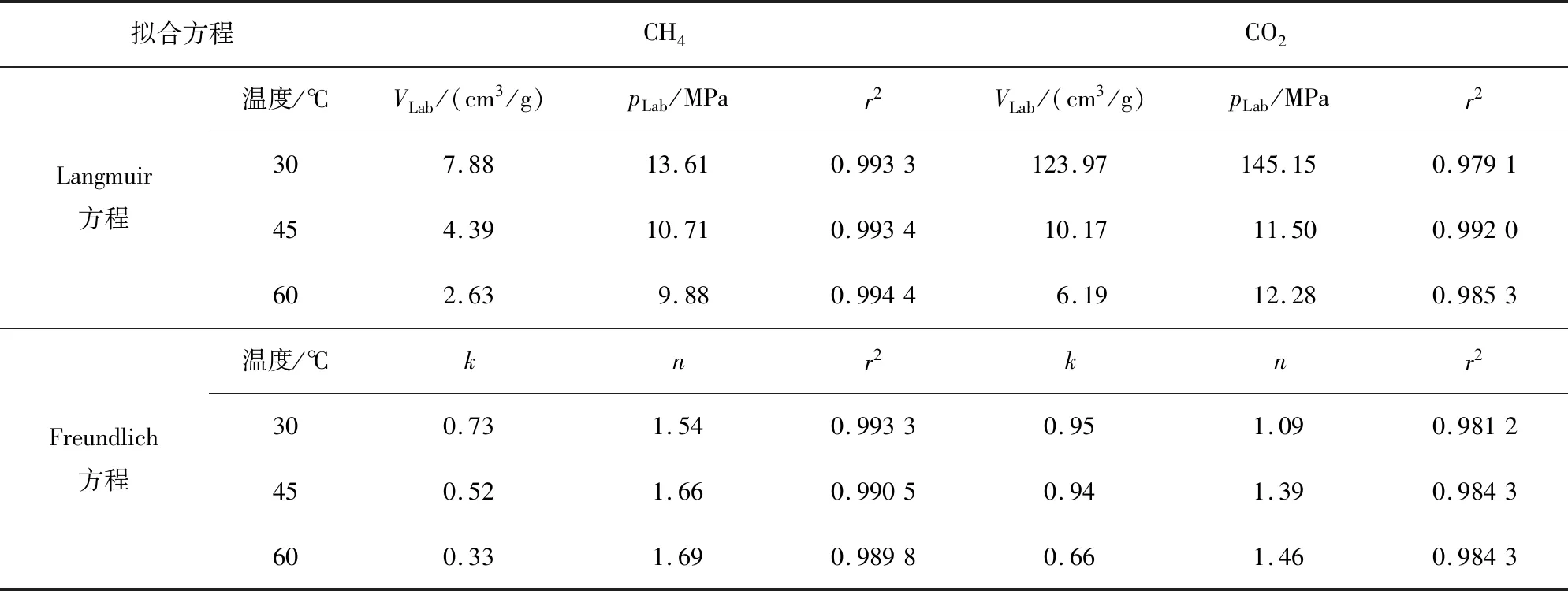
表3 绝对吸附量曲线的Langmuir方程及Frenudlich方程拟合参数Tab.3 The fitting parameters of Langmuir and Frenudlich equations
5 等量吸附热特征分析
5.1 等量吸附热计算方法
等量吸附热指温、压、吸附剂表面积恒定时,吸附1 mol气体发生的焓变[2],可间接反映吸附强弱及吸附剂表面的不均匀性。通常通过Clausius-Clapeyron方程[17]计算:
(5)
其中qst为等量吸附热,J/mol。将式(5)两端变形并进行积分,可得
(6)
其中C2为积分常数。式(6)表明,1/T和lnp呈线性关系,由斜率可得到吸附量n对应的等量吸附热qst。假设斜率为A则等量吸附热为
qst=-RA。
(7)
5.2 延长组页岩过剩等量吸附热和绝对等量吸附热特征
为后续叙述方便,将基于过剩吸附量计算获得的等量吸附热简称为过剩等量吸附热,基于绝对吸附量计算获得的等量吸附热简称为绝对等量吸附热;相对于初始等量吸附热,分别简称为过剩初始等量吸附热及绝对初始等量吸附热。
分别采用线性函数式(8)和幂函数式(9)对基于过剩和绝对吸附量的压力对数-吸附量(lnp-n)数据进行函数拟合。
lnP=a1+b1nex,
(8)
(9)
其中:a1、b1、a2、b2、c为拟合函数参数;nex为过剩吸附量,mol/g;nab为绝对吸附量,mol/g。lnp-n数据函数结果如图7所示。拟合结果表明,基于过剩吸附量的lnp-n数据符合线性函数拟合,基于绝对吸附量的lnp-n数据符合幂函数拟合。
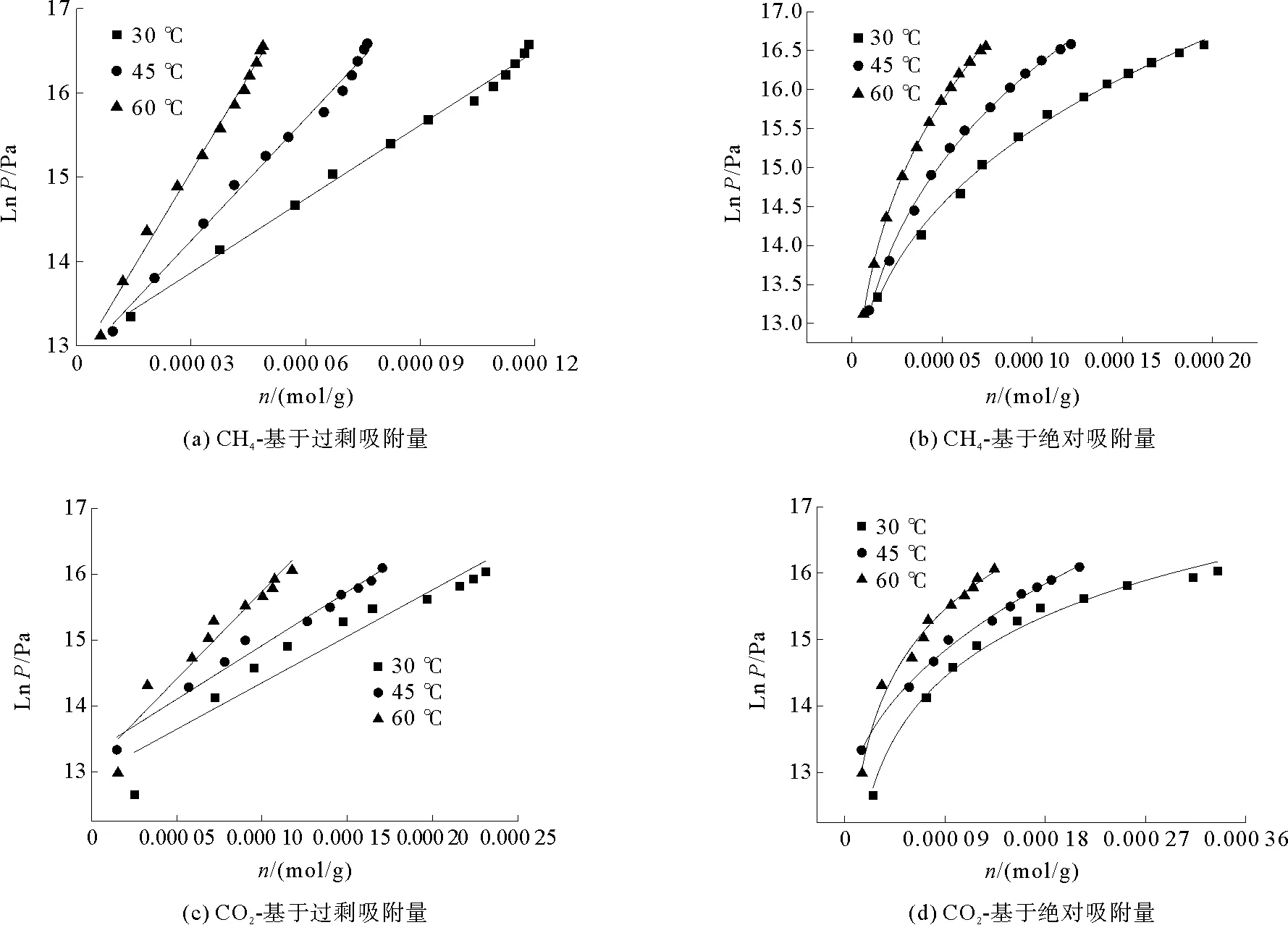
图7 基于不同类型吸附量的lnp-n拟合曲线Fig.7 The fitting curve of lnp-n under different types of adsorption capacity
利用式(8)、式(9)计算若干吸附量下的lnp,对压力对数-温度倒数(lnP-T-1)数据进行线性拟合,拟合函数为
lnP=AT-1+B。
(10)
其中A、B为拟合参数。基于不同类型吸附量的lnP-T-1拟合曲线如图8。拟合结果表明,针对不同类型吸附量的lnp-T-1数据符合线性变化规律,同时基于绝对吸附量的lnp-T-1的线性函数拟合相关系数平均在0.98以上,拟合程度高。
依据式(7)结合lnp-T-1拟合函数斜率计算等量吸附热。延长组页岩吸附CH4、CO2的过剩与绝对等量吸附热曲线如图9所示。由图9可知,延长组页岩吸附CH4的等量吸附热大于CO2,过剩等量吸附热大于绝对等量吸附热,且随吸附量增加,差值逐渐增大。
采用线性函数对等量吸附热与吸附量进行拟合,线性拟合方程表示为:
qst=a3+b3n。
(11)
其中:a3、b3为拟合常数,a3表征初始等量吸附热,J/mol;b3反映了等量吸附热的变化率,J/mol。等量吸附热与吸附量的线性拟合曲线及参数如图9、表4所示。
由表4可见,对于页岩吸附CH4,过剩初始等量吸附热小于0,这与吸附过程为放热过程的事实不符,说明吸附热力学分析应以绝对吸附量为基础。

图8 基于不同类型吸附量的lnp-T-1拟合曲线Fig.8 The fitting curve of ln p-T-1 under different types of adsorption capacity
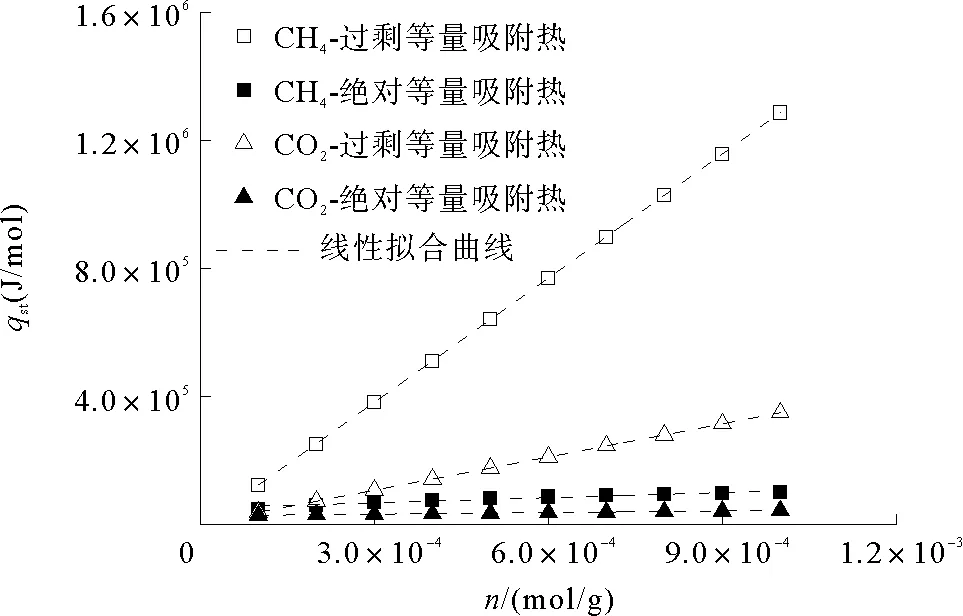
图9 基于不同类型吸附量的等量吸附热曲线Fig.9 The isosteric heat of adsorption under different types of adsorption capacity
等量吸附热计算表明,页岩吸附CH4和CO2的等量吸附热与吸附量满足线性正相关关系,原因是受吸附剂表面的非均质性和吸附质分子间作用力的影响,而吸附剂表面非均质性决定了吸附质分子首先在高活性位点优先吸附,而后逐渐在弱活性位点吸附,造成了吸附热随吸附量的增加而减低;另外,吸附质分子间的作用力随吸附量增加而增强,因而吸附热增加[18]。
相同吸附体系下,初始等量吸附热反映了吸附剂与吸附质间的作用力,初始等量吸附热越大,则吸附剂表面对气体分子的作用力越大[6]。由表4可知,当n=0时,页岩吸附CH4和CO2的绝对初始等量吸附热分别为52.04和27.71 kJ/mol,说明延长组页岩对CH4的吸附作用力较CO2强,但无法用工程实践论证,原因是本次实验CH4和CO2的吸附实验是独立进行的,而实际储层中的置换过程中CH4解吸与CO2吸附是同时进行的,存在CH4与CO2分子间的相互作用,体现在热力学上便是解析热与吸附热的相互影响。
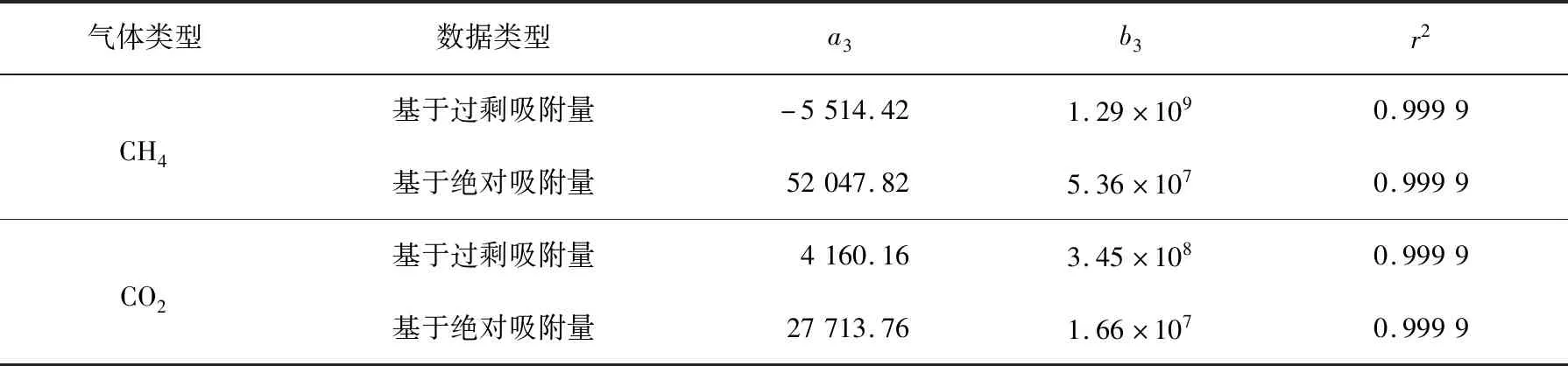
表4 等量吸附热与等温吸附量的线性拟合参数Tab.4 The linear fitting parameters of isosteric heat and adsorption capacity
6 结论
1)绝对吸附量大于过剩吸附量,二者差值受温压条件及气体类型的影响,随温度升高而减小,随压力升高而增大,且吸附气为CO2时,二者差值较CH4大。
2)对吸附过程的热力学分析应当选用绝对吸附量作为基础数据,原因在于过剩等量吸附热存在低吸附量阶段的负值现象,与吸附放热的事实相矛盾,同时相较于绝对等量吸附热明显偏高。
3)延长组页岩吸附CH4和CO2的等量吸附热与吸附量间满足良好的线性正相关关系,且吸附CH4的等量吸附热大于吸附CO2的等量吸附热,页岩吸附CH4和CO2的绝对初始等量吸附热分别为52.04和27.71 kJ/mol,说明延长组页岩对CH4的吸附作用力强于CO2。

