判别类条件贝叶斯网络分类器的量子粒子群优化参数学习

吴慧玲1 ，丁晓彬，贺广生1，刘久富

(1.河南牧业经济学院 智能制造与自动化学院，河南 郑州450046；2.南京航空航天大学 自动化学院，江苏 南京210016)

贝叶斯网络[1](Bayesian networks,BN)是一种利用概率统计方法，对不确定性问题进行分析和推理的工具。贝叶斯网络被认为是不确定性知识表达和推理的最有效理论模型之一。一方面，贝叶斯网络能够通过图论清晰地解释问题的结构；另一方面，贝叶斯网络能够利用明确的问题结构简化概率推理的复杂性。而贝叶斯网络分类器(Bayesian network classifiers,BNC)是一种基于统计的典型分类模型，不仅具有贝叶斯网络的优点，而且适用于处理分类问题。目前，贝叶斯网络分类器的高效训练是研究的热门话题。其中，生成学习和判别学习方法是主要的参数学习方法。生成学习方法解决联合分布的参数估计问题；而判别学习方法解决后验分布的参数估计问题，直接计算P(y|x)，对分类问题更加高效。

贝叶斯网络及其分类器被广泛应用于各大领域中。在图像处理方面，文献[2]将非静态贝叶斯网络用于处理视频检测问题；在故障诊断方面，文献[3]基于贝叶斯网络，提出一种高效联合树推理算法；在医疗诊断方面，文献[4]从不完全统计中构建出贝叶斯医学诊断网络。在处理液体火箭发动机的故障诊断与分类方面，文献[5]采用动态云BP网络进行故障诊断，但神经网络需要大量的训练数据，这对于故障数据获取困难的液体火箭发动机来说，无疑是一个难题。

提出的贝叶斯网络分类器的判别类条件网络模型，是由类条件贝叶斯网络模型经过对数形式重新参数化得到的。通过量子粒子群算法对其优化求解，得到各节点的概率，完成分类任务。改进后的分类器用于液体火箭发动机的故障诊断与分类中，能够高效完成分类任务，与朴素贝叶斯分类器和TAN分类器相比，分类准确率和训练效率显著提高。

1 贝叶斯网络分类器的参数学习

1.1 贝叶斯网络分类器

贝叶斯网络B=〈G,Θ〉由结构G(一个有向无环图，其中每个节点表示一个变量Zi)和一组参数Θ组成，其中，Θ是与贝叶斯网络相关的参数集，这些参数可以量化结构内的依赖关系。变量Y=Z0表示类别，变量X1=Z1,X2=Z2,…,Xn=Zn，称为属性，其中n表示属性的数量。参数Θ由结构G中的每个节点的一组表示局部条件概率分布的参数θΣn|Πn(x)和θzi|y,∏i(x)组成，其中1≤i≤n，Πi(.)是一个函数，其功能是给定数据实例x=〈x1,x2,…,xn〉作为输入，返回结构G中节点i的父节点值，其中xi∈Xi，表示属性Xi的第i个属性值。为了标记简单，将θZ0=z0|Π0(x)和θZi=zi|y,Πi(x)记为θz0|Π0(x)和θzi|y,Πi(x)。其中，θZi=zi|Πi(z)表示给定父节点时，变量Zi取值为zi的概率；Π0(.)表示类的父节点。

若给定某一数据实例x=〈x1,x2,…,xn〉，则贝叶斯网络的联合概率分布为：

(1)

式中，y∈Y，表示类变量的取值，与z0相同。

根据贝叶斯定理，相应的条件概率分布PB(y|x)为：

(2)

在本文的分类问题中，类变量是所有属性变量的父节点，将θy|∏0(x)记为θy，即θy|∏0(x)=θy。

给定一组数据D={x(0),…,x(N)}，其中N表示数据点的数量，那么贝叶斯网络的对数似然函数(Log-Likelihood，LL)为：

(3)

约束条件为：

(4)

在公式(4)的约束条件下，通过使公式(3)取最大值的方法优化参数θ即为参数的最大似然估计。

1.2 类条件贝叶斯网络模型

使用贝叶斯网络分类器进行分类，通常按照两个步骤，其中步骤1涉及最大化联合概率P(y,x)，步骤2则是根据贝叶斯定理获得条件概率P(y|x)。而本文直接通过最大化条件对数似然函数(Conditional Log-Likelihood，CLL)来优化P(y|x),由于直接优化了从样本特征到类标签的映射，因此对于分类问题更加高效。

根据贝叶斯定理，条件对数似然函数定义为：

(5)

如果贝叶斯网络结构是正确的，最大化对数似然函数和条件对数似然函数应该具有相同的结果[9]。因为θ没有闭形解，使得条件对数似然函数取最大值；因此，必须在参数空间上求助于数值优化方法。

与任何贝叶斯网络模型一样，类条件贝叶斯网络模型由图形结构和量化属性间依赖关系的参数θ组成。对于贝叶斯网络B，相应的类条件贝叶斯网络模型基于网络B*(其中B*是基于贝叶斯网络B的类条件贝叶斯网络)，通过将条件对数似然函数最大化求得其参数。将Ross等[10]提出的定义稍作修改：

定义1对具有严格正参数集θB*的网络B*，若从属性集(X1,X2,…,Xn)到类变量Y上的分布的所有函数集合采用等式(2)的形式，则称这类基于网络B*的条件分布集合为类条件贝叶斯网络模型，记为MB*。

本文类变量的父节点为空集合，则表示类变量的参数记为θv(j)。

1.3 判别类条件贝叶斯网络模型

朴素贝叶斯结构是生成模型，通过优化公式(3)获得模型参数。逻辑回归(logistic regression，LR)与朴素贝叶斯结构存在一定的联系，但LR是一种通过优化公式(2)获得相关参数的类条件贝叶斯网络模型。通常，逻辑回归学习每个属性变量(每个类)的权重。然而，可以通过考虑合理的二次、三次或更高阶特征的全部子集或部分子集来扩展逻辑回归。根据Roosetal[9]，将判别类条件贝叶斯网络定义为：

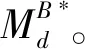
重新定义公式(5)中的P(y|x)：

(6)

根据定义2，重新定义公式6中与每个参数θ相关联的参数β：

logθy=βy，logθxi|y,Πi(x)=βy,xi,Πi

现在公式(6)变为：

(7)

(8)

由于上式没有闭形解，本文将采用量子行为粒子群的优化算法对模型进行优化求解。

2 量子行为粒子群算法

2.1 算法的主要思想

传统的PSO(particle swarm optimization,粒子群优化)算法的主要缺点是容易陷入局部最优解。针对这一问题，孙俊等[10]提出一种量子行为粒子群算法(quantum behaved PSO,QPSO)，使粒子拥有跳出局部最优解的机制。在QPSO算法中，粒子的运动与传统的PSO算法完全不同。在量子领域里，速度和位置的更新不能同时确定，因此牛顿定理在量子领域是不成立的。粒子的新状态由波函数ψ(x,t)确定。另外，文献[11]指出，粒子位置的概率密度函数由|ψ|2表示。文献[12]的轨迹分析表明，如果种群中的每个粒子收敛到定义的局部吸引子，则PSO算法收敛。其中，局部吸引子的定义为：

(9)

(10)

其中，i=1,2,3,…,N且j=1,2,3,…,D。N为种群中粒子的数量，D为粒子的维数。r1和r2服从均匀分布，c1和c2是PSO算法部分的固定值。粒子群的新位置由以下公式确定：

(11)

其中，xi,j表示第i个粒子的第j维位置；β是收缩-扩展系数[11]，通过调整β可以加速算法的收敛。u和rnd是0到1之间服从均匀分布的随机数；pi,j是式(10)中定义的局部吸引子；Mbest是种群中粒子Pbest位置的均值。则Mbest可由下式计算：

(12)

另外，在种群中具有最佳适应度值的被称为全局最优，记作Gbest，是这一代粒子的最佳解决方案。

2.2 算法的实现步骤

设置的终止条件为迭代次数大于200次。

综合上文所述算法的主要思想，量子行为粒子群优化(QPSO)算法的具体实现步骤为：

1)初始化种群中的粒子位置为随机位置；

2)计算每个粒子的适应度值；

3)根据式(12)计算Mbest向量；

4)将每个粒子的适应度值与Pbest进行比较，如果当前适应度值优于Pbest，则将当前适应度值设置为新的Pbest值，并在D维空间中更新；

5)将Pbest与Gbest进行比较，如果Pbest优于Gbest，则用当前Pbest替换Gbest；

6)根据式(11)更新粒子的位置；

7)重复步骤2)到6)，直至满足算法的终止条件。

3 实例分析与验证

Weka系统是由新西兰Waikato大学开发的一个开放源码的机器学习及数据挖掘系统。本研究采用的验证工具基于Weka系统，并对其在功能上进行补充和修改，使之成为适用于液体火箭发动机故障诊断的数据挖掘平台。

3.1 数据的预处理

采用的数据样本是某大型氢氧发动机36次仿真试车的数据，通过建立大型氢氧液体火箭发动机的数学模型，对该型号的液体火箭发动机可能发生的各类故障进行多次仿真得到测试数据。其中30次为正常数据，6次为故障数据，共7 500个样本。6组故障数据分别是：发生器氢副控阀泄露、氢涡轮出口燃气泄露、氧稳压阀出口泄露、发生器氧副控阀泄露、氧涡轮入口燃气泄露及氧泵后泄露。原始样本数据量非常庞大，而且测量的参数种类繁多，如果不进行数据预处理，将会在很大程度上影响分类的精度与优化速度。

首先选取原始仿真数据中共同存在的70多个参数数据，从其中选择数值相对稳定的数据40多个。再进一步从中选择易发故障部分组件的相应参数22个，作为最终参与分类的属性参数。同时，由于实际数据变化较大，数据的数量级有可能差别很大，为了提高分类及优化效率，采用如下公式对数据进行归一化处理：

(13)

式中，Xij为第i个样本中第j个属性的值，Xj为数据样本中第j个属性的均值。

3.2 改进分类器与各分类器的对比

3.2.1 改进分类器的构建

树扩展朴素贝叶斯网络(tree-augmented naive Bayesian network，TAN)利用贝叶斯网络中的依赖关系，对朴素贝叶斯结构进行扩展，放宽了朴素贝叶斯网络中的独立性假设条件，是对朴素贝叶斯网络的改进。TAN分类器能够接纳属性之间的依赖关系，使其更加符合实际情况。

将判别类条件贝叶斯网络模型与TAN分类器相结合，通过最大化条件对数似然函数，获得各节点的参数。将新的分类器记为TANd分类器。TANd分类器在数据量较小时分类优势不够明显，但是当数据量的规模增加，各参数的属性之间的独立性假设条件不再被满足时，普通的贝叶斯网络分类器的分类精度会大幅下降，而TANd分类器的分类效果依然能够保持很高的分类精度。利用TANd分类器对液体火箭发动机进行故障诊断的具体步骤如下：

步骤1将预处理后的故障数据和常规数据组合构成训练集，根据训练集生成TANd分类器模型；

步骤2利用生成的TANd分类器模型对液体火箭发动机进行故障诊断。

由于液体火箭发动机的各参数之间并非完全相互独立，因此，采用TANd分类器时，各属性参数之间存在一定的联系。TANd分类器通过计算不同属性之间的条件互信息函数，在属性间添加弧，建立一个有向无环图。

根据样本集训练生成的TANd分类器模型如图1所示。除类节点外，每个节点至多只有一个属性节点作为其父节点。例如，PK为燃烧室压力。除类节点外，POR(代表氢泵入口压力)也是其父节点。图中各节点的依赖关系也反映出实际情况中属性之间的依赖关系。

图1 基于仿真数据集的TANd网络模型Fig.1 TANd model based on simulation data

3.2.2 改进分类器与各分类器的诊断结果对比

为了验证提出方法的有效性，将其与朴素贝叶斯分类器和TAN分类器进行比较。其中，朴素贝叶斯分类器和TAN分类器采用WEKA平台提供的算法，分别记为NBC和TNC。实验采用10重交叉验证，采用最小描述长度离散化方法对连续型数值进行离散化。采用的训练集为完整数据训练集，不含缺失值，其中包含液体火箭发动机的正常运行数据及6种故障数据，共计7个类变量，得到集合{发生器氢副控阀泄露、氢涡轮出口燃气泄露、氧稳压阀出口泄露、发生器氧副控阀泄露、氧涡轮入口燃气泄露及氧泵后泄露，正常}，记为{Fault1，Fault2，Fault3，Fautl4，Fault5，Fault6，Normal}。

使用三种贝叶斯分类器对仿真数据集进行故障诊断与分类，实验结果如表1～2所示。

表1 三种分类器的实验结果对比Tab.1 Comparison of experimental results of three classifiers

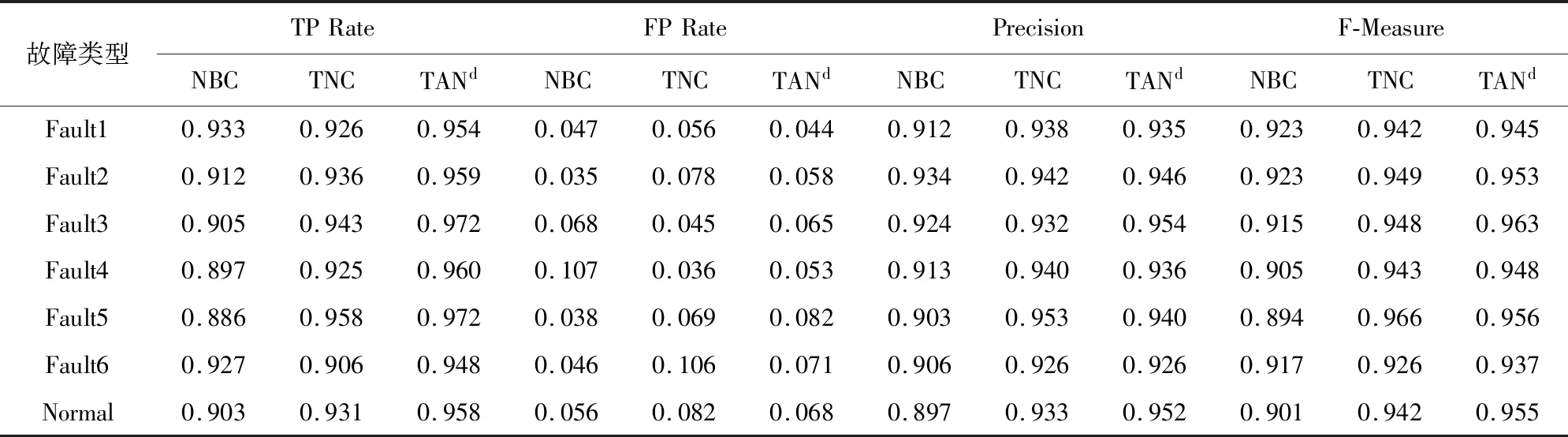
表2 三种分类器对故障类型的具体分类结果对比Tab.2 Comparison of specific classification results of various types of fault types by three classifiers

表1～2中TP Rate表示被模型预测为正的正样本率，FP Rate表示被模型预测为正的负样本率，Precision为查准率，Recall为召回率，F-Measure为Precision和Recall的加权调和平均，其值越接近1，表明诊断方法越有效。从表1中可以看出，在分类准确率、召回率这两项指标上，本研究的改进分类器要优于TAN分类器，且上述两个分类器都明显优于朴素贝叶斯分类器。从F-measure指标中可以看出，本研究的改进分类器的评价结果最接近于1。

从表2中的三种分类器的详细分类结果可以看出，本方法对于每种故障分类的准确率均能达到95%左右，明显优于朴素贝叶斯分类器，同时也略优于TAN分类器。

表3 三种分类器的均方根误差对比Tab.3 Comparison of root mean square error of three classifiers

由表3可知，本方法对分类结果的均方根误差小于朴素贝叶斯分类器和TAN分类器，同样表明了本方法的分类效果好，分类结果稳定，验证了本方法的有效性。

3.3 收敛性分析

针对PSO算法容易陷入局部极值，随机性和智能性不足的缺点，本研究采用的QPSO优化算法不依赖于粒子的速度、粒子的位置及概率密度由波函数产生。在粒子位置有界的情况下，算法满足全局收敛性条件，能够依概率收敛至全局最优解。

设置算法的参数，令c1=c2=2，设置种群规模N=20。当算法迭代次数大于200次时，算法终止。

图2所示为量子粒子群算法优化TANd分类器的演化曲线。可以看出，算法在进化开始时，收敛速度很快，能够快速逼近问题的最优解。此外，算法根据粒子位置的有界性，能够依概率收敛至全局最优解，在大约80次迭代之后，就会限制粒子的搜索范围，围绕最优解进行搜索，且没有陷入局部极值，算法具有良好的稳定性。

与神经网络等智能算法相比，所验证的分类器不需要大量的数据集，且分类器的训练用时很短，分类的准确率较高，在对算法进行优化时，迭代次数少，且能够快速逼近最优解，这对于数据样本收集困难的故障分类工作具有重要的意义。

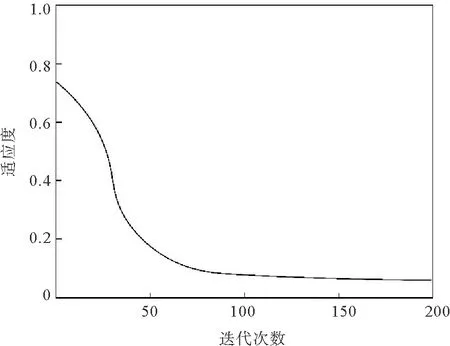
图2 分类器在仿真数据集上的演化曲线Fig.2 The evolutionary curve of simulation data

4 结论

1)针对液体火箭发动机的故障诊断问题，基于类条件贝叶斯网络的参数学习，将判别贝叶斯网络模型与TAN分类器结合，构建TANd分类器，并根据贝叶斯定理和最大后验概率原则对训练集进行分类，判断是否属于故障数据，或者是故障中的哪一类。

2)改进的分类器在分类精度上优于朴素贝叶斯分类器和TAN分类器，同时分类的误差较小，分类器的稳定性较好，能够有效处理分类问题。

3)采用的量子行为粒子群优化算法能够有效对TANd模型进行优化，迭代次数少，优化效率高。

下一步将针对模型的优化问题，将贝叶斯网络的生成和判别参数方法结合起来，构建基于参数权重的判别网络模型，进一步提高模型的优化效率。