带拉条多腔钢板混凝土组合剪力墙抗震性能研究

(1.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590；2.江苏建筑职业技术学院，江苏 徐州 221116)

21世纪我国建筑工业化发展进程不断推进，国家先后出台大量政策，提倡装配式建筑产业的发展。装配式组合结构相对于装配式混凝土结构自重轻、技术成熟、应用方便；相对于装配式钢结构稳定性好、耐久性优、成本更低廉，具有广阔的应用前景。双钢板-混凝土组合剪力墙由于起步较晚，体系尚未完善。在国外，Eom等[1]按缩尺比例对5个矩形和T形截面的双钢板组合剪力墙进行低周往复试验，分析了截面形式、钢板厚和墙肢数对其抗震性能的影响。Choi等[2]进行了双钢板混凝土组合剪力墙的轴压试验，研究了混凝土材料、钢板厚度对剪力墙破坏及屈服形式的影响，并提出了钢板表面屈曲应力的简化评定准则。Epackachi等[3]进行了钢板混凝土剪力墙的试验和有限元分析，分析了不同参数对于组合剪力墙的影响。开发了用于组合剪力墙非线性挠曲的简化分析模型。Asl等[4]对不同形式梁截面削弱的钢板剪力墙进行了数值模拟，结果表明在梁腹板中开槽的形式延性更好，具有最佳的抗震性能。在国内，武晓东等[5]采用不同加载方式研究了剪跨比对双钢板短肢组合剪力墙受力性能的影响，结果表明当剪跨比取2.0时试件的变形能力更好。姜拯民等[6]采用纤维截面模型叠加剪切弹簧考虑剪切效应，基于OpenSees程序，建立双层钢板组合剪力墙有限元分模型，分析了不同参数抗震性能的影响。郭晓农等[7]提出一种开洞双钢板组合墙结构，研究了洞口对试件抗震性能的影响，墙体开洞虽然会影响抗侧刚度和承载力，但变形能力有所改善，对抗震较为有利。从上述文献可以看出对于双钢板组合剪力墙的研究已经较为成熟，但是设有约束拉条的多腔钢板组合剪力墙研究却仍处于起步阶段。

本研究在已有钢板混凝土剪力墙试验和理论研究的基础上[8-11]，提出一种带拉条多腔钢板混凝土组合剪力墙，首先对该形式的组合剪力墙进行拟静力试验，研究不同轴压比和高宽比对其抗震性能的影响，并利用有限元软件Abaqus进行数值分析，与试验结果进行对比；在此基础上，改变高宽比、钢板厚、轴压比、混凝土强度、拉条间距等参数，对20个带拉条多腔钢板混凝土组合剪力墙模型在往复荷载作用下的承载力和抗震耗能性能进行深入研究，得出不同参数对该形式的组合剪力墙抗震性能的影响，旨在为带拉条多腔钢板混凝土组合剪力墙结构的设计提供参考。

1 试验概况

1.1 试件设计

设计带拉条多腔钢板混凝土组合剪力墙：剪力墙两端为方钢管，中间为具有内折部分的连接钢板，钢板依次焊接，两端与方钢管焊接为整体，沿墙厚方向的一对内折钢板由拉条焊接连接，墙体内部浇筑混凝土，共设计3片剪力墙，编号为CSW1、CSW2、CSW3，试件构造如图1所示。

试件缩尺比例为1/2，均采用Q345级钢，混凝土等级C40，加载梁中心到基础顶面1 600 mm，厚80 mm。墙宽根据高宽比不同分别为800和1 120 mm；试件两端边缘处分别设有80 mm×80 mm方钢管混凝土柱，钢板厚度为3 mm，方钢管壁厚3 mm，两侧钢板在墙厚方向由拉条进行拉结，拉条选用与钢板等强钢材，钢板边缘内折20 mm，方便拉条搭接施焊，搭接长度为10 mm，搭接处采用三面围焊，各试件拉条宽度20 mm，厚度3 mm，间距取80 mm，钢板与钢板、钢板与边缘方钢管之间均采用开坡口的等强对接施焊，焊缝采用E4311焊条焊接，焊缝等级达到2级。各试件尺寸及变化参数见表1。

1.2 加载制度

加载装置示意如图2所示。首先预加反复荷载50 kN一次，然后施加竖向轴压力，并保持竖向轴压荷载不变；水平加载时首先由荷载控制，由100 kN开始，每级增加50 kN至试件屈服；然后改为位移控制，按照屈服位移Δy的整数倍逐级加载，每级循环三次，直到破坏为止。

2 试验结果

试验中剪力墙的破坏状态主要为：①弹性阶段，试件荷载-位移曲线基本为直线，基本没有残余变形，墙体钢板与混凝土部分界面发生粘结破坏，但对曲线没有影响，试件也无屈曲变形现象；②屈服阶段，墙体钢板与内填混凝土的粘结破坏仍在继续，试件底部边缘方钢管及靠近方钢管的钢板出现屈曲现象，且屈曲程度和范围不断发展，轴压比增大，试件底部钢管和钢板的屈曲出现比较早，钢板鼓曲程度也相对严重。高宽比越小，试件刚度越大，峰值荷载越大，但对应的位移较小；③破坏阶段，随着位移加大，水平承载力开始逐渐减小，试件底部屈曲程度进一步发展，钢板及方钢管屈曲严重，钢管侧面开裂，混凝土压溃，水平承载力下降到峰值荷载的85%，即认为其丧失承载能力，试件破坏。试件最终破坏模式基本上都是组合墙体底部300 mm范围内的钢板和方钢管受压达到屈曲，内部混凝土被压碎，钢板(钢管)鼓曲开裂。试件破坏形式如图3所示。

图1 试件设计构造详图Fig.1 Detailed drawings for testing components

表1 各试件尺寸及变化参数Tab.1 Size and parameters of individual specimen

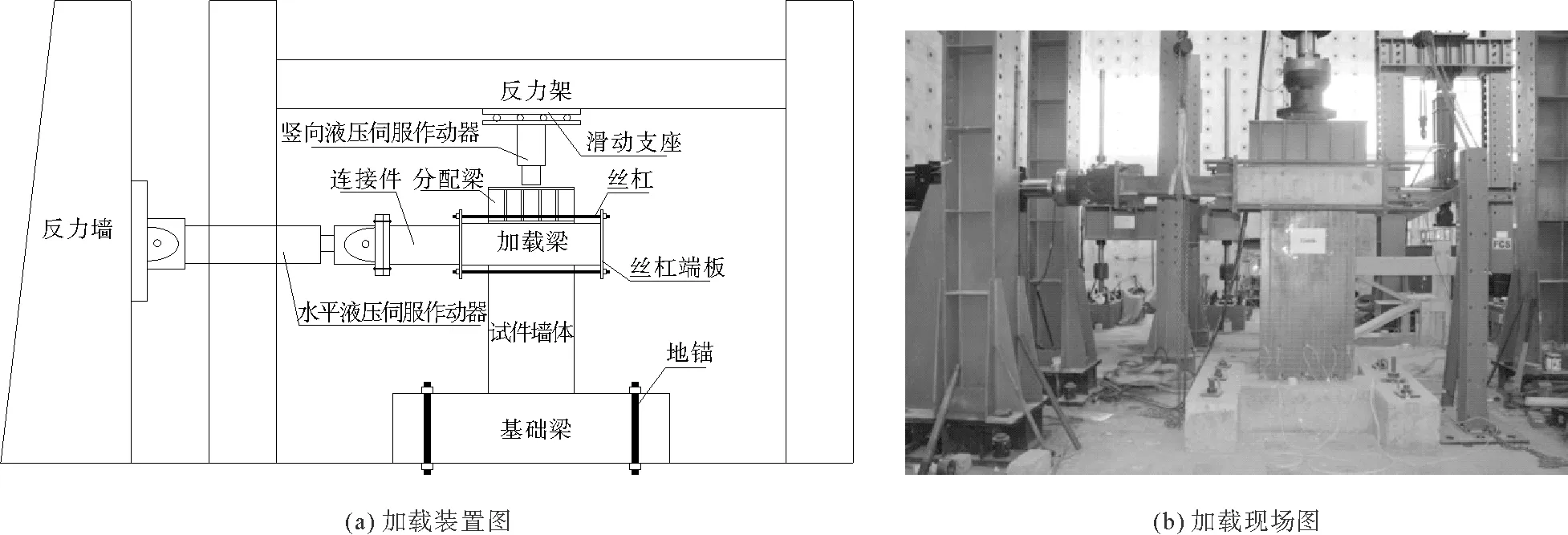
图2 加载示意图Fig.2 Schematic diagram of loading

图3 剪力墙试件破坏照片Fig.3 Photographs of failure shear walls

3 有限元建模及分析

3.1 有限元模型建立

选用损伤塑性模型来模拟混凝土的弹塑性和损伤，如图4所示。由于材料拉压性能的差异，通过破坏能量准则来定义混凝土受拉软化作用，利用非相关塑性势能流动法则来定义混凝土塑性损伤模型中的混凝土受拉和受压行为，采用的塑形势能由Drucker-Prager双曲函数确定。模拟钢材时选用弹-塑性强化本构模型，根据经验将钢板的屈服强度和弹性模量折减20%，并对钢板屈服后的刚度进行修正[12-13]，修正后的钢材本构模型如图5所示。

各试件均采用C3D8R单元，组合墙中方钢管、钢板及连接拉条均采取焊接连接，不考虑焊接残余应力及焊接损伤，因此选择Tie约束模拟传力情况，其中方钢管、钢板及连接拉条在组装时已经选取merge选项代替焊接；混凝土与钢材之间的接触面是由两部分相互约束组成：分别为接触面的法向约束和切向约束，其中法向约束选取“硬约束”模拟，切向约束选择摩擦系数0.6的“罚”接触模拟，网格划分如图6所示，荷载及边界条件如图7所示。

图4 混凝土本构模型Fig.4 Constitutive model of concrete

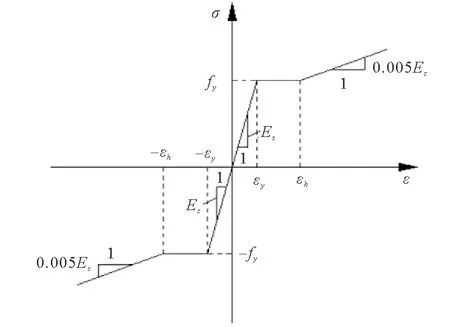
图5 钢材本构模型Fig.5 Constitutive model of steel

图6 网格划分Fig.6 Grid partition of the model

图7 荷载及边界条件Fig.7 Load and boundary conditions

3.2 有限元结果

模拟的破坏形态如图8所示。模拟结果中，试件CSW1的破坏开始于墙脚两侧的局部屈曲，随着位移的不断增大，屈服范围向中间扩大，整个墙脚部分进入屈服状态。CSW2的破坏状态与试验中一致，随着加载位移不断增大，剪力墙首先在墙脚两侧发生屈服，继而向墙脚中部发展，最终以剪力墙墙脚鼓曲破坏。CSW3的模拟结果比试验中的破坏状态更加明显，破坏过程为在墙脚两侧鼓曲，逐渐向墙脚中部发展。

图8 有限元模型破坏图Fig.8 Failure pictures of the finite element model

3.3 试验与有限元结果对比

各试件有限元与试验滞回结果对比如图9所示。有限元得到的墙体滞回曲线更为饱满、圆滑，且刚度较大。这是因为：数值模拟的材料本构关系与试验存在一定差异，模拟时不能真正反映混凝土在低周反复荷载作用下“裂缝闭合行为”影响，且在试验时存在焊接变形及残余应力等初始缺陷，试验装置间的缝隙、支撑及加载部件对试件的摩擦等都会产生影响。此外有限元接触模拟无法展现试验中试件的真实情况，未能反映钢材与混凝土间实际的粘结滑移。虽然模拟结果与试验略有差别，但整体上可以体现试件在往复荷载作用下的发展全过程。

图9 滞回曲线对比Fig.9 Comparison of the hysteresis curves

各试件有限元与试验骨架曲线结果对比如图10所示。对比试件CSW1与CSW2可以发现，在高宽比一定时，CSW2承载能力有一定提高，初始弹性刚度也相对较大，即增大剪力墙试件的轴压比可以一定范围内提高试件弹性刚度和承载能力，但承载力增加幅度较小且下降时间早于CSW1。相比CSW1，高宽比更小的CSW3在相同轴压比下的刚度和承载力显著提高，变形能力相差不大，承载力下降趋势都比较缓和，即减小试件高宽比对试件承载力和刚度的提高显著，对其延性和变形能力影响不大。

图10 骨架曲线对比Fig.10 Comparison of the skeleton curves

4 组合剪力墙抗震性能影响参数分析

4.1 影响参数

为研究不同参数对组合剪力墙试件抗震性能的影响，分别改变高宽比、钢板厚度(含钢率)、混凝土强度、轴压比、拉条间距等参数进行数值分析计算，模型参数变化如表2所示。

表2 模型参数表Tab.2 Parameters of shear wall model

4.2 不同参数对骨架曲线的影响

不同参数试件的骨架曲线如图11所示。图11(a)反映了高宽比对骨架曲线的影响，加载初期，随着位移不断增大，高宽比越小，剪力墙所承受荷载增加越快，即高宽比越小初始刚度越大；随着高宽比减小，峰值承载力有显著提高；达到峰值荷载后，试件反力不再增大，而是随位移的增大出现小幅度降低，反映出试件良好的变形能力。图11(b)反映了钢板厚度对骨架曲线的影响，随着钢板厚度增加，试件承载力有明显提高：钢板厚度为5 mm时，剪力墙的峰值承载力最高。图11(c)反映了混凝土强度对骨架曲线的影响，随着混凝土强度等级提高，水平抗剪承载力有所提高，提高幅度不大，但由C30至C70，水平抗剪承载力提高了31.15%，相较而言，纯钢剪力墙承载力大幅降低。图11(d)反映了轴压比对骨架曲线的影响，初期轴压比的变化对剪力墙的初始刚度影响不大；轴压比由0.3增至0.5时，峰值承载力逐步提高，轴压比由0.5增至0.6时，剪力墙的承载力没有明显变化，轴压比由0.6增加至0.7时，剪力墙的承载力反而下降。图11(e)反映拉条间距对骨架曲线的影响，随着拉条间距加密，承载力不断提高，从无拉条到拉条间距为120 mm，承载力提高明显。

图11 不同参数骨架曲线对比Fig.11 Comparison of the skeleton curves with different parameters

4.3 不同参数对刚度退化的影响

通过环向刚度来研究不同参数对试件抗震性能的影响。环向刚度越大，说明其下降率越小，试件的耗能能力就越强。环向刚度计算公式为：

(1)

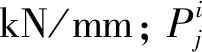
不同参数试件的刚度退化曲线如图12所示。图12(a)反映了高宽比对刚度曲线的影响，速度都是由快变慢，最终趋于平缓；高宽比大的试件初始刚度比高宽比小的试件显著减小；高宽比越小，剪力墙的刚度退化速度越快。图12(b)反映了钢板厚度对刚度曲线的影响，钢板厚度越大，剪力墙的刚度越大；三种不同钢板厚的剪力墙刚度退化速度均由快变慢，最终趋于平缓，趋势大致相同，刚度退化速度无明显差异。图12(c)反映了混凝土等级对刚度曲线的影响，不同强度等级的混凝土其刚度退化速度均由快变慢，最终趋于平缓；混凝土强度较高时，初始刚度较大，且初始加载阶段，混凝土强度高的试件刚度退化速度略快；但在加载位移达到10 mm之后，不同混凝土强度的试件刚度差距不再明显，相较于组合剪力墙，纯钢剪力墙退化速度更加显著。图12(d)反映了轴压比对刚度曲线的影响，不同轴压比的试件墙刚度退化速度均由快变慢，最终趋于平缓，不同轴压比剪力墙在加载至50 mm时退化至相近大小的刚度值；随着轴压比的增大，剪力墙的刚度先增大再减小，但增大、减小的幅度都很小。图12(e)反映了拉条间距对刚度曲线的影响，有拉条的剪力墙刚度明显比无拉条的剪力墙刚度大。

图12 不同参数刚度曲线对比Fig.12 Comparison of the stiffness degradation curves with different parameters

4.4 不同参数对等效粘滞阻尼系数的影响

耗能能力是衡量试件抗震能力的重要指标，反映了自身消耗地震的能量。试件的滞回曲线包络的面积越大，其耗能能力越强。采用能量耗散系数E和等效粘滞阻尼系数he来衡量各试件的耗能能力，计算公式如式(2)所示。

(2)

式中：SABC+SCDA为曲线中某滞回环面积，mm2，相当于结构在该循环所储存的能量；SOBE+SODF为曲线中某滞回环上下荷载峰值点与坐标原点连线所围的三角形面积之和，mm2。

不同参数试件的滞回曲线面积与位移关系如图13所示。图13(a)反映了高宽比对曲线的影响，高宽比不同，曲线滞回环面积均随位移的增大而增大，且同一加载级别高宽比越小试件滞回环面积越大，即高宽比越小耗能量越大。图13(b)反映了钢板厚度对曲线的影响，加载位移相同时，剪力墙的钢板越厚，滞回曲线包围的面积越大，即同样位移钢板较厚时剪力墙的耗能量比较大。图13(c)反映了混凝土强度对曲线的影响，随着混凝土强度增大，滞回曲线包围的面积略有增大。相对于采用C30混凝土，采用C70混凝土50 mm位移对应的剪力墙耗能面积增大了1.91%，增大幅度有限，相较于组合剪力墙，纯钢剪力墙耗能明显降低。图13(d)反映了轴压比对曲线的影响，同一加载级滞回面积随轴压比的增大先增大后减小，轴压比为0.6时对应的耗能面积最大，轴压比为0.3时对应的耗能面积最小，轴压比为0.7时对应的耗能面积介于轴压比0.3～0.4之间。图13(e)反映了拉条间距对曲线的影响，随着拉条间距变小，滞回曲线包围的面积会增大，即拉条间距越小耗能量越大；位移为50 mm时，拉条间距为80 mm的剪力墙相对于无拉条剪力墙的值提高了10.73%。

图13 滞回曲线面积与位移关系Fig.13 Relationship between the hysteresis areas and displacements

不同参数等效粘滞阻尼系数与位移的关系如图14所示。图14(a)反映了高宽比对曲线的影响，高宽比小的剪力墙等效粘滞阻尼系数较大，在初始加载阶段差距比较明显，加载后期差距减小，高宽比越小耗能性能越强。图14(b)反映了钢板厚度对曲线的影响，加载至50 mm时，4和5 mm厚钢板的试件相对于3 mm厚钢板的试件等效粘滞阻尼系数分别提高了3.95%和6.99% 。图14(c)反映了混凝土强度对曲线的影响，在加载初期，混凝土强度高的试件等效粘滞阻尼系数稍大，加载后期，混凝土强度高的剪力墙等效粘滞阻尼系数反而偏小，相较于组合剪力墙，纯钢剪力墙耗能能力明显降低。图14(d)反映了轴压比对曲线的影响，等效粘滞阻尼系数在轴压比为0.3～0.5时，随轴压比增大略有增大，轴压比在0.5～0.7时，等效粘滞阻尼系数先略微增大后略微减小，变化程度较小。图14(e)反映了拉条间距对曲线的影响，剪力墙的耗能性能随拉条的加密略有提高，但影响不大。

5 结论

带拉条多腔钢板混凝土组合墙作为新型抗侧力构件，抗震性能及承载能力良好。试验结果验证了数值模拟的正确性，利用有限元软件Abaqus对不同影响参数的试件进行低周往复荷载作用下的模拟，得到以下结论：

1)高宽比对剪力墙的承载力影响较大，在其他条件相同的情况下，高宽比越小剪力墙的承载能力越强，耗能性能略有提高，但同时延性变差；钢板厚度对剪力墙承载能力、耗能性能等都有较大影响，一般而言钢板越厚，剪力墙的承载能力和耗能性能越优，但成本增加。

2)混凝土强度增大时剪力墙的承载力略有提高，但变形能力变差，耗能能力在初始阶段较好，后期相反；轴压比主要影响剪力墙的延性，当轴压比过大时剪力墙延性明显下降。因此实际应用时应注意合理控制剪力墙的轴压比；与此同时，相较于纯钢剪力墙，组合剪力墙结构的抗震性能明显提高。

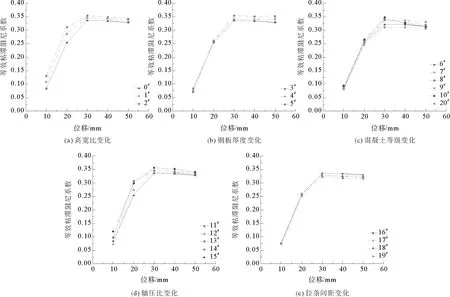
图14 等效粘滞阻尼系数与位移的关系Fig.14 Relationship between equivalent viscous damping coefficients and displacements

3)设置拉条对钢板的平面外变形及混凝土和钢板之间的滑移影响较小，拉条间距减小时剪力墙的延性和承载能力略有提高，拉条的重要性需要更多的试验验证，其间距的合理设置需要在建模时考虑更多因素进行验证。

4)研究结果表明，组合剪力墙轴压比不宜超过0.6、高宽比不宜超过2、缀板间距不宜超过120 mm，同时混凝土强度等级取C50、钢材厚度取3～4 mm时，组合剪力墙构件的抗震性能优良且经济。