单裂缝简支梁动静刚度变化规律分析及试验研究

魏安清

（石家庄市交建高速公路管理有限公司平赞分公司，河北石家庄 050000）

对于完好的简支梁，通过结构频率可以反推出结构的动刚度EId。通过挠度可反推出结构的静刚度EIs，理论上有EId=EIs。由于结构动力特性测试简单快捷，部分学者对“以动代静”快速评估结构状态的相关方法进行了研究，并初步应用于工程实践［1-4］。但中小跨径简支梁桥常用的钢筋混凝土梁正常使用阶段可能发生受力开裂，相关研究表明，已受力开裂的钢筋混凝土简支梁动静刚度存在明显差异，但两者动静刚度差异产生原因及相关关系有待进一步研究［3-6］。本文基于单裂缝Euler-bernoulli简支梁挠度及频率计算公式，讨论单裂缝简支梁的动刚度、静刚度变化规律以及两者间的关系，最后通过4片矩形截面钢筋混凝土简支梁分级加载开展相关试验研究。

1 单裂缝简支梁挠度及频率理论公式

结构裂缝的模拟方法主要有3类：分离的弹簧模型、局部刚度折减、实体有限元分析。本文采用分离的弹簧模型，在结构裂缝处把结构分成独立的2部分，通过加入转动弹簧模型来模拟裂缝。

文献［7］中的转动弹簧模型表示为

式中：Keq为弯曲弹簧的刚度系数；E为简支梁的弹性模量；I0为完好截面抗弯惯性矩；h为矩形梁的高度；β为归一化裂缝深度；β=d/h；d为裂缝深度；C(β)=β(2-β)/0.9(1-β)2。

令1/EI（x）为Euler梁的抗弯柔度，对于无损伤等截面梁其为常数；对于损伤梁，裂缝会导致该处抗弯柔度增大。为了使问题简化，引入狄拉克δ函数，利用裂缝处局部柔度的跳跃性增大来模拟裂缝的影响。具体表达式为

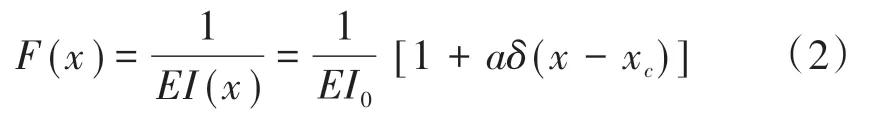
式中：1/（EI0）为完好梁的抗弯柔度；a为裂纹导致的附加弯曲柔度系数；xc为裂纹到简支梁左支点的距离。

根据裂缝处的变形协调条件，推导得到

根据简支梁的边界条件，通过结构力学方法推导可得到单裂缝简支梁挠度及频率的计算公式。

均布力作用下单裂缝简支梁的挠度计算公式为

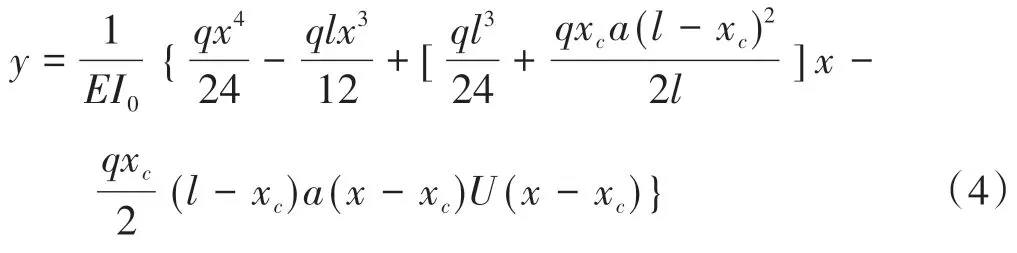
式中：q为均布力；l为计算跨径；x为计算位置。

当无裂缝时，a=0，xc=0，得到挠度公式为

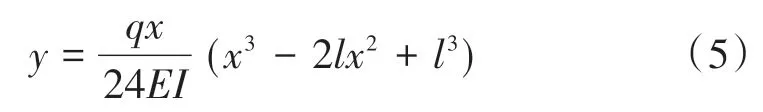
集中力作用下单裂缝简支梁挠度的计算公式为

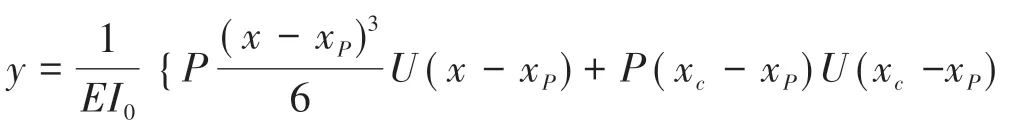
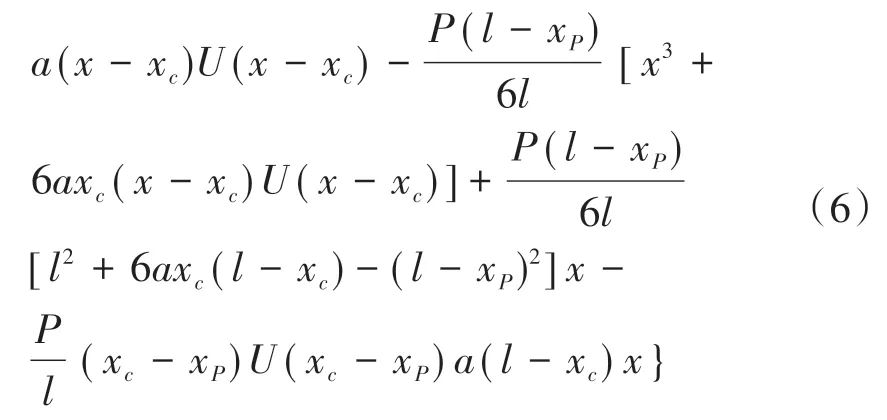
式中：P为集中力；xp为其作用位置；U（x-xp）为阶跃函数，x-xp≥0时U（x-xp）=1，否则为0。

当无裂缝时，得到集中力作用下挠度计算公式

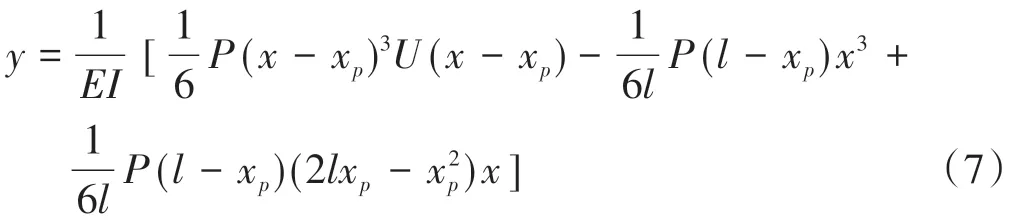
单裂缝简支梁的频率计算正则方程为

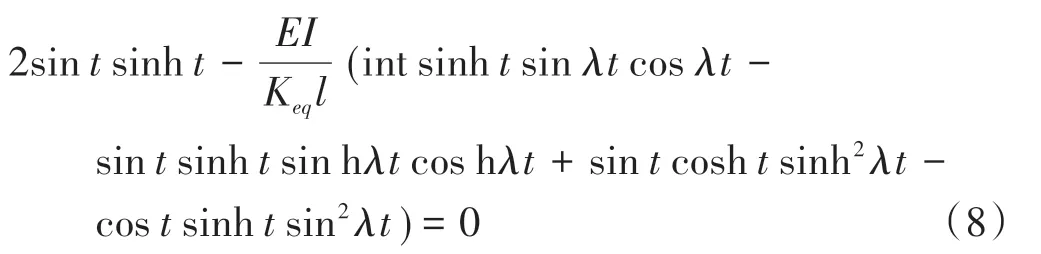
式中：λ=xc/l；t=βl；β4=ω2m/EI，ω=2πf。

由式（8）求出t，即可求得简支梁的频率f。式（8）为超越方程，本文采用数值方法进行求解。

当简支梁完好时λ=0，式（8）可简化为sintsinht=0；对应频率公式为

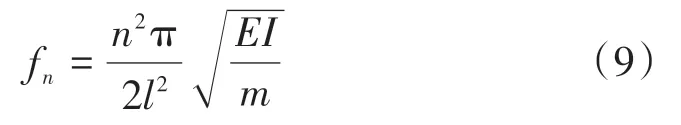
2 单裂缝简支梁动静刚度变化规律

理论计算模型是计算跨径为3.20 m 的简支梁，截面尺寸b×h=0.15 m×0.25 m，弹性模量取34.5 GPa，材料密度取2 600 kg/m3。取裂纹深度为0.4h进行分析，计算时取均布力q=10 kN/m，集中力P=20 kN。完好简支梁跨中挠度均为2.03 mm，一阶频率为40.33 Hz，二阶频率为161.31 Hz。

荷载作用下跨中挠度与裂缝相对位置的关系见图1。可以看出，加载方式对裂缝梁跨中挠度影响很大，跨中集中力作用下的挠度远大于均布力作用下的挠度；同一加载方式，裂缝越靠近跨中，对应的挠度值越大。

频率与裂缝相对位置的关系见图2。可以看出，裂缝位于振型节点时，对该阶频率无影响，裂缝离振型节点越远对应频率值越小。

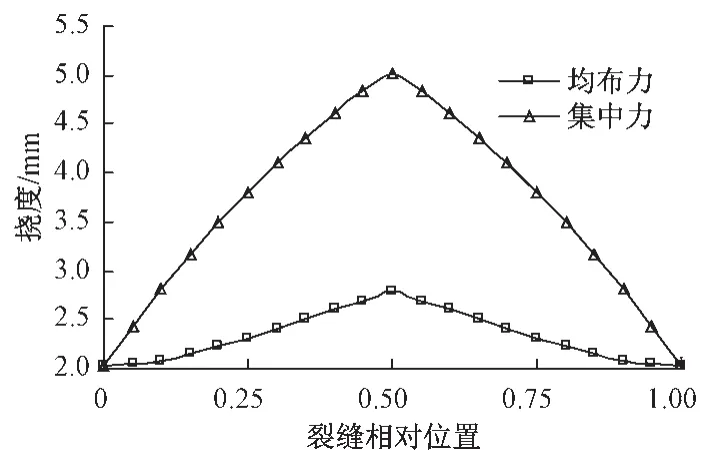
图1 荷载作用下跨中挠度与裂缝相对位置的关系

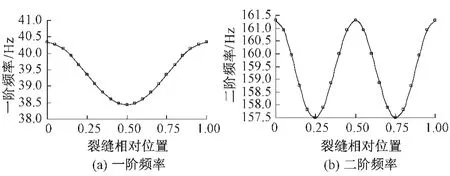
图2 频率与裂缝相对位置的关系

由裂缝梁在荷载作用下的挠度按照式（5）、式（7）反算得到简支梁的静刚度EIs。由裂缝梁的频率按照式（9）反算得到简支梁的动刚度EId。为了方便分析，将反算得到的刚度除以结构完好时对应的刚度得到归一化刚度。不同位置裂缝对简支梁归一化静刚度、动刚度的影响见图3。

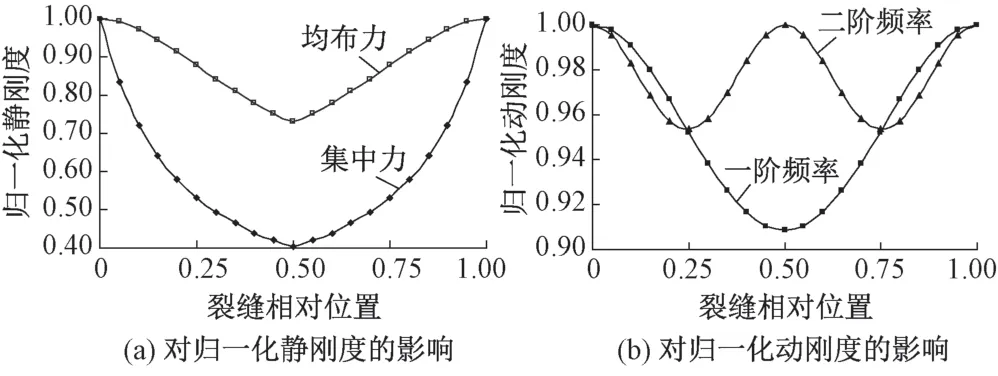
图3 裂缝位置的影响

由图3可以看出，通过跨中挠度反算得到的结构静刚度与加载方式有关。对于同样的裂缝位置，均布力作用下跨中挠度反算静刚度大于跨中集中力作用下的跨中挠度反算静刚度。通过频率反算得到的动刚度与频率阶次有关。裂缝位于振型节点时对反算动刚度无影响，裂缝离振型节点越远对结构动刚度影响越大。

对比图3（a），图3（b）可以看出，一阶频率反算得到的动刚度随裂缝位置变化规律与静挠度反算得到的静刚度类似，但动刚度大于对应的静刚度。因此，要建立开裂简支梁动刚度与静刚度之间的关系，应以一阶频率为主。

3 钢筋混凝土简支梁试验研究

3.1 试验过程简述

模型试验用钢筋混凝土简支梁为矩形截面梁，共4 片梁，梁高0.15 m，梁宽0.25 m，梁长3.5 m。受力主筋采用5 根直径12 mm 的HRB335 钢筋，保护层厚度为25 mm，箍筋采用双肢直径8 mm 的R235钢筋，箍筋间距为125 mm。结构混凝土采用C50，经实测混凝土密度为2 471 kg/m3，计入钢筋质量计算得到简支梁单元长度质量为102.8 kg/m。在支点、1/4点及跨中梁底各布置1个挠度测点，共有5个挠度测点。挠度测点对应梁顶各布置1个加速度测点，共5个加速度测点。

静载试验采用机械千斤顶分级加载，千斤顶顶部设压力传感器以便控制加载压力。试验时简支梁的两支点间距为3.2 m。其中1，2 号梁采用分配梁两点加载方式，加载位置距离两侧支点1.10 m，跨中纯弯段1.00 m；3，4 号梁采用跨中单点加载方式。频率测试采用力锤激振，每次频率测试前卸去千斤顶、分配梁等，保证梁体附加质量。锤击位置距跨中20 cm，每级荷载下锤击15次，取平均频率作为对应等级荷载作用后简支梁的实测频率。

3.2 试验结果分析

每片梁均加载至梁体开裂破坏、荷载不能稳定时为止。实测得到各级荷载P作用下试验梁跨中弹性挠度y及一阶频率f1见表1。

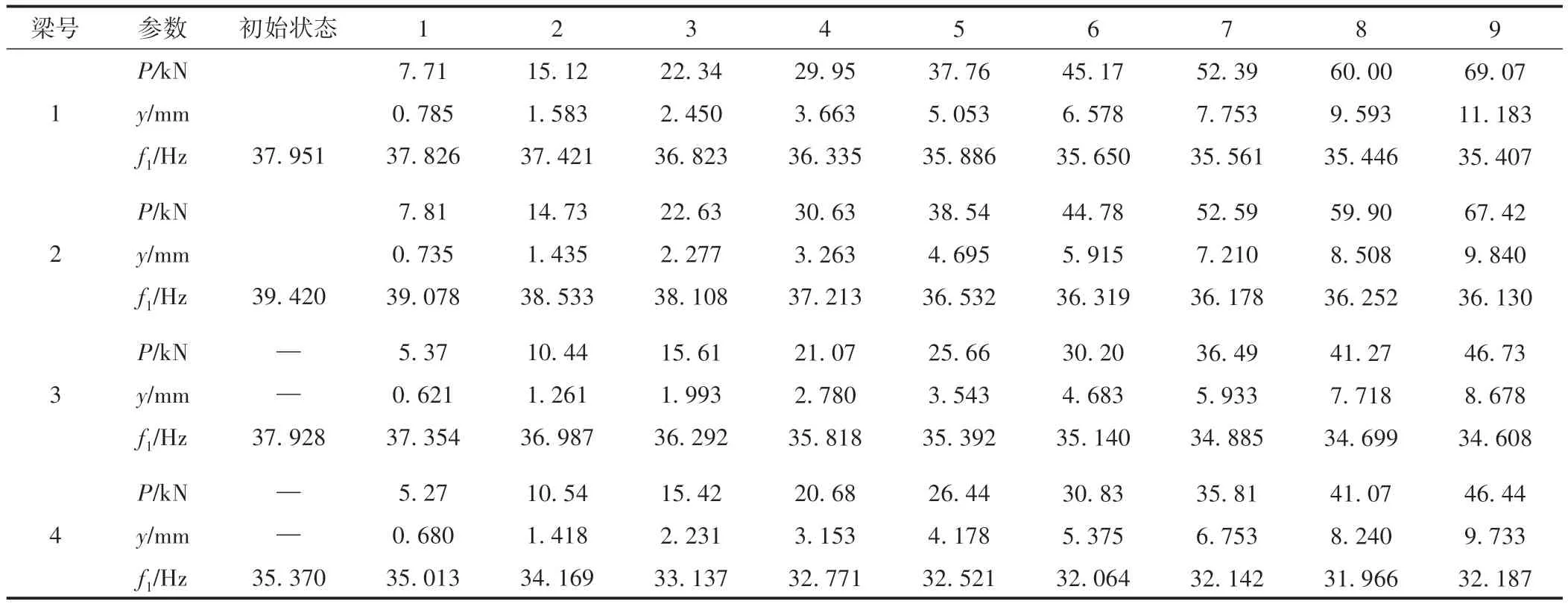
表1 各试验梁实测结果

参照第2 节的方法，由试验梁在荷载作用下的挠度按式（7）反算得到简支梁的静刚度EIs，由试验梁一阶频率按照式（9）反算得到简支梁的动刚度EId。试验过程对梁体裂缝发展情况进行观测（见图4），第一级加载时各试验梁均未见开裂，本文认为试验梁初始状态时的静刚度与第1级加载后静刚度相同。

图4 试验梁裂缝发展示意

各级荷载加载后的反算刚度除以试验梁初始状态的刚度得到归一化刚度。各片试验梁在各级荷载作用后的归一化刚度变化见图5。可以看出，随着试验荷载的增加，各试验梁的动刚度、静刚度都有逐渐变小的趋势；在加载初期裂缝初步发育的时候，试验梁动刚度、静刚度变化基本一致；随着荷载的增大梁体裂缝进一步发育，静刚度下降较快，动刚度大于静刚度。这与前面的分析结论是相符的。

图5 梁归一化刚度变化

4 结论

1）单裂缝简支梁动刚度与频率阶次相关，裂缝位于振型节点时对动刚度无影响，裂缝离振型节点越远对结构动刚度影响越大，应采用一阶频率计算动刚度。

2）钢筋混凝土简支梁在裂缝初始发育时动刚度、静刚度变化基本一致；梁体裂缝进一步发育后，静刚度下降较快，动刚度大于静刚度。

3）钢筋混凝土简支梁开裂初期可用实测结构基频代替荷载试验了解结构的刚度情况，但梁体开裂严重时应谨慎使用这种方法。

4）钢筋混凝土简支梁动刚度、静刚度变化趋势分界点对应的裂缝状态（高度、宽度、间距等）尚需针对不同截面形式开展进一步研究。