基于正交实验的库水位骤降边坡渗透稳定敏感性分析
郝 忠 周 峰 付 操 张英姿
(1.镇江市港口发展集团有限公司运营管理分公司,江苏镇江 212000;2.镇江市建设工程管理处,江苏镇江 212000;3.镇江市建设工程质量监督站,江苏 镇江 212000)
库水位变动是影响库区边坡稳定的重要因素[1-2],库水位会导致土体内部浸水导致强度降低[3];减小土体的有效应力[4];边坡的水压突然卸载,导致边坡的突然失稳[5];边坡迎水面的浸润线呈现“滞后”现象,使得渗流力指向坡外[6].库区周边居民常常因库区边坡的失稳破坏,而遭受生命财产的严重威胁,同时边坡失稳也会对水工建筑及库容构成损伤,因此,有必要对库水位骤降引起的边坡稳定和渗流特性进行研究.
影响库水位变动下的边坡稳定性因素较多,其中土体的非饱和性质对边坡的渗流特性以及稳定性影响较大,如曾铃[7]对粗粒土不同非饱和性质在降雨条件下的渗透稳定性进行了分析;唐栋[8]对不同非饱和Fredlund&Xing参数下的降雨渗流特性以及安全系数的变化进行了研究;刘海宁[9]对库水位变化下的不同非饱和性质下的土堤稳定性进行了数值模拟,以上研究均发现土体的非饱和参数对土体的渗流特性以及稳定性具有一定的影响,但是均未定量研究不同非饱和参数对边坡的影响程度大小,对于边坡稳定性数值模拟中,参数的取值对正确模拟工况的影响较大,因此定量研究非饱和参数对边坡渗透稳定性的影响对正确评估影响边坡稳定性的敏感因素,保证数值模拟的可靠性产生重大意义.
现行的敏感性分析方法主要分为单因素敏感性分析与多因素敏感性分析,单因因素敏感性分析较之多因素敏感性分析来说主要存在分析参数少,参数之间无法考虑非独立情况[10]等不足,而正交实验分析法能够研究多个非饱和参数变化对边坡稳定性的影响,例如陈坤杰[11]利用正交试验分析法对边坡的内摩擦角、粘聚力、高度、重度、地震加速度进行了敏感性分析;邹沐[12]通过正交试验法对材料参数、水位及其相关荷载、地震作用等对边坡安全系数计算值的影响进行了研究.鉴于正交试验分析法的便捷及准确性,因此本文以三峡库区某滑坡体为例,基于Fredlund & Xing提出的非饱和理论[13],选取了土体非饱和参数a,m,n,k,利用Geo-slope软件中的Seep/w和Slope/w模块,基于正交实验分析法对某边坡的渗透稳定性进行了敏感性分析,为相应的工程提供了定量化参考.
1 计算理论
1.1 非饱和理论
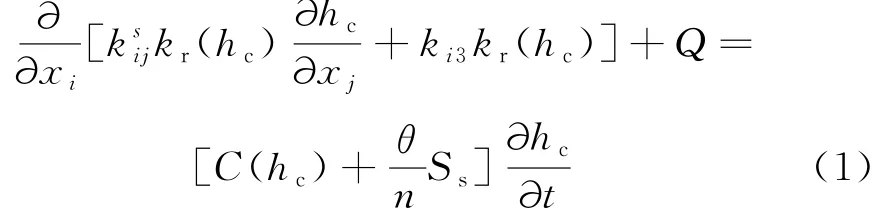
根据非饱和渗流理论[14],其控制方程为:式中,Q表示源汇;C(hc)表示饱水时容水度;Ss表示贮水量单位值;k ij表示渗透张量;kr为相对透水率;hc表示压力水头高度;n为孔隙率;θ为压力水头函数.
应用Fredlund&Xing[7]模型建立土水特征曲线,控制方程如下:

式中,Cφ表示修正函数,本文根据文献[15]取值1;θs表示土体的饱和体积含水量;θw表示体积含水量;φ表示负孔隙水压力;e为自然对数。设定拟合参数为a,m,n,其中a较进气值略大(k Pa),表征体积含水量的拐点;m控制残余含水量;n控制体积含水量函数的斜率.
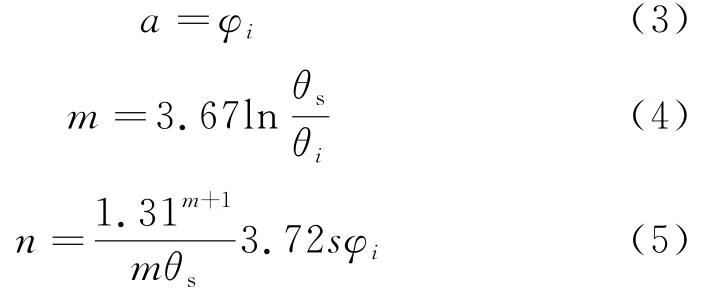
式中,φi为曲线拐点对应的基质吸力;s为拐点处的斜率.
根据Geo-slope的Seep/w模块的控制方程[15],由式(2),已知θs,可估算出渗透系数函数:
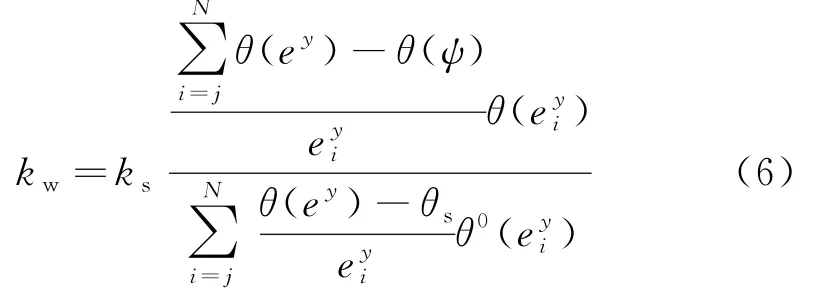
式中,kw为通过负孔压或者含水量计算得到的渗透系数;ks为饱和渗透系数;i为j到N间的数值的间距,j和N分别表示函数最终所描述的最小负孔压和最大负孔压;y代表按负孔压计算的虚拟变量;ψ表示与第j步相对应的负孔压;θ0表示方程初始值.
1.2 非饱和抗剪强度理论
由于滑坡土体内部的饱和及非饱和区域在库水位变动下始终处于变化状态,因此采用非饱和理论[13,16].
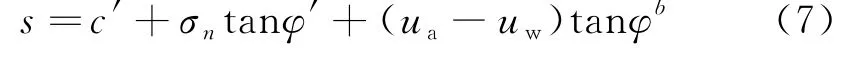
式中,c'与φ'表示有效强度;ua和uw分别表示孔隙空气压力和孔隙水压力;σn为孔隙气压力与法向总应力的差值;φb表示在负孔压影响下提高的强度.
2 计算模型
2.1 计算模型及边界
计算模型如图1所示,坡比为1∶2,坡脚高度h=7 m,边坡高度H=14 m.为实时监测库水位骤降时土体内部不同位置位移和孔压的变化,分别设置上部和下部监测点.假设初始条件为13 m水头以下,左边界abcd和右边界gh均为的稳定渗流场。边界ah,defg均为不透水;abcd表示随库水位变动的区域边界,随着时间的变化,边界cb上各节点的水头值也不断变化,软件运行中,当节点高程大于节点水头,则该节点的流量Q则为0;边界gh为13 m定水头。图2所示为计算模型的网格图划分,本文模型包含628个单元和513个节点,网格尺寸约为1 m.

图1 计算模型
模型网格图如图2所示,计算单位全局网格尺寸约为1 m,一共剖分为513个节点及628个单元.
图2 模型网格
2.2 计算工况及参数
根据文献[16]模型的材料参数取值为:土体密度ρ=1.8 g/cm3,c'=12 kPa,φ'=21°,E=0.12 GPa,μ=0.27,k=0.02 m/d,a=10 k Pa,m=1,n=4.设定工况为库水位从13 m高程的正常蓄水位以1 m/d的速率下降至7 m的死水位高程,计算时长考虑水位下降结束后的第14 d,总时长则为20 d.当k,a,m,n值改变时,分别计算边坡土地的渗透稳定性,见表1.

表1 计算工况
3 结果分析
3.1 渗流场分析
图3~4表示上部和下部监测点在不同工况下孔压的变化规律.可以看出,监测点的孔压受不同非饱和参数a,m,n,k的影响时变化较大,主要存在以下规律:
1)上部监测点与下部监测点的孔压随时间,下降速率呈现先快后慢,最后趋于稳定的规律,上部监测点的孔压降幅较下部监测点要小.
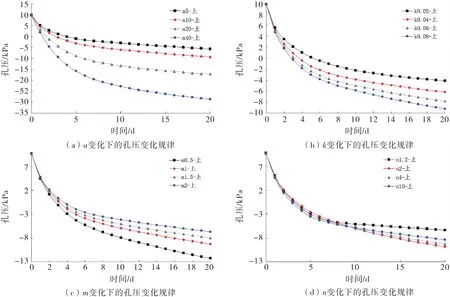
图3 上部监测点孔压变化规律
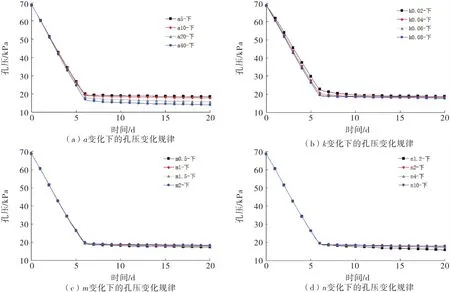
图4 下部监测点孔压变化规律
2)对于上部监测点来说,孔压降幅与参数a,k呈负相关,而与参数m呈正相关,对于参数n来说,孔压前期变化较为一致,而在后期n值越大,孔压的降幅越大.
3)对于下部监测点来说,孔压在库水位骤降前期变化较小,而在后期略有变化,孔压变化的大小与上部监测点类似.
3.2 监测点位移分析
不同非饱和参数土体在库水位骤降下上部监测点与下部监测点的位移变化规律如图5~6所示.由图5~图6可见:
1)库水位骤降情况下上部监测点与下部监测点存在两个变形阶段,即库水位骤降时间段内的位移快速上升阶段以及库水位骤降结束后的位移缓慢上升阶段.
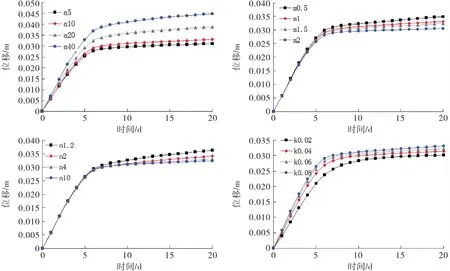
图5 上部监测点位移变化规律
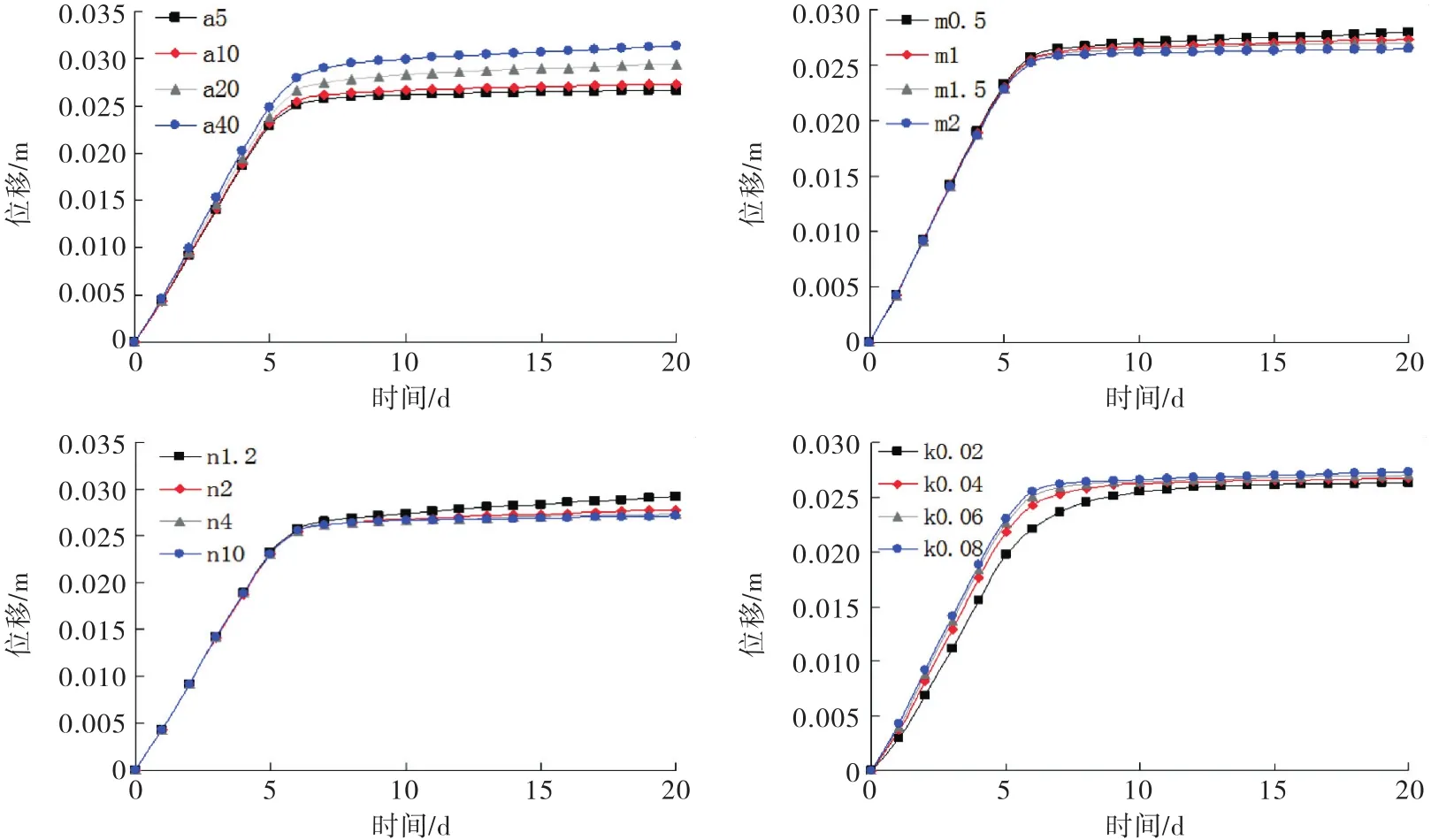
图6 下部监测点位移变化规律
2)参数a对边坡在库水位骤降情况下的变形量影响最大,上部监测点的最大变形量在3.1~4.8 cm之间,而下部监测点的最大变形量在2.7~3.4 cm之间;参数m,n,k则影响较小,上部监测点的平均最大变形量在3.1~3.3 cm之间,而下部监测点的平均最大变形量在2.7~2.9 cm之间.
3)上部监测点的位移要大于下部监测点的位移.
3.3 安全系数变化
不同工况下的安全系数变化如图7所示.
1)不同工况的安全系数随着库水位骤降的变化规律较为一致,总体下降速率呈现先快后慢,最后趋于稳定的趋势.安全系数前期变化较块,而在后期变化较慢.
2)边坡的稳定性受不同非饱和参数的影响存在敏感性差异.安全系数的变化幅度受m与n变化的影响相对较低;但在工况A、D条件下,受a与k变化的影响较大,可以看出,当a=5时安全系数最小值为0.99,此时边坡土体为失稳状态.
3)参数a越小,安全系数越小,参数m越大,安全系数越大,参数n越大,安全系数越小,参数k越大,安全系数也将变大.
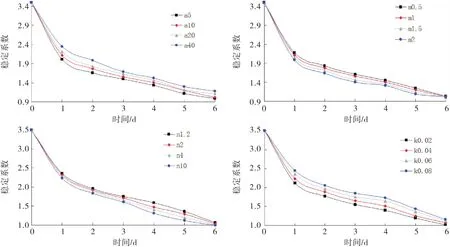
图7 不同工况安全系数变化
3.4 正交试验敏感性分析法
3.4.1 正交试验设计原理
正交试验法是基于数理统计方法,选择具有代表性的工况进行敏感性分析的一种方法,具有均衡分散性和整齐可比性两大特点,可以较少的试验次数反映事物的客观变化规律[12].
正交试验表具有以下两个特点:每一列(因素)的不同水平在试验中出现的次数相同;任意两列(因素)的不同水平组合在试验中出现的次数相同.正交表用L n(t c)表示,其中:L代表正交表的代号;n为总试验次数;t为因素的水平数;c为正交表列数,即可以安排的最多的因素个数.以四因素四水平情况为例,其正交试验表见表2.
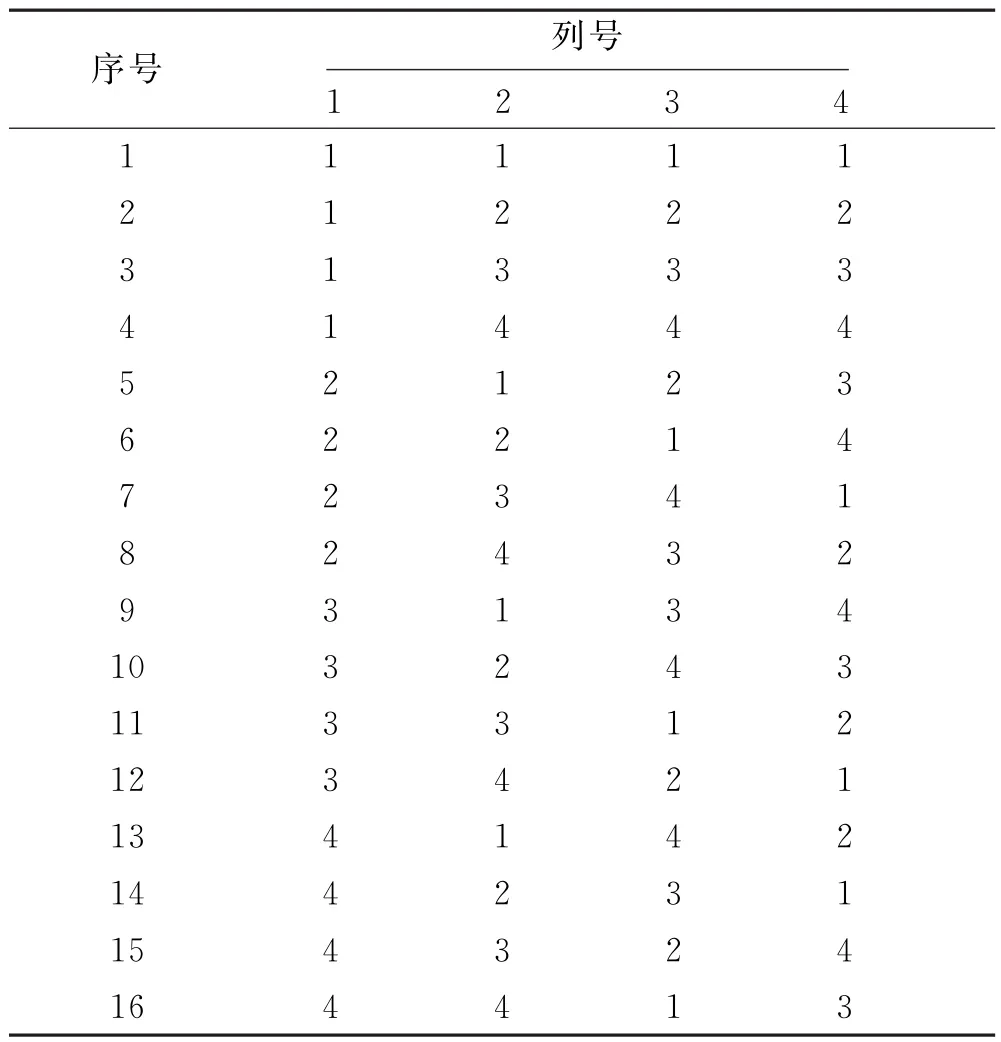
表2 四因素四水平正交试验表
按照表2所设计的正交表进行试验分析,计算各个指标的敏感性大小的方法主要分为极差分析与方差分析两种[13],而极差分析通过计算各因素在各水平下的平均值以及极差,较方差分析简单易操作,因此本文选择极差分析进行试验的敏感性分析.
3.4.2 正交试验法敏感性分析
用不同非饱和参数a,m,n,k的变化作为试验的因素,而最小安全系数作为评价指标列入表中,各个因素选取4个水平进行分析.以最小安全系数构建的正交试验表见表3.
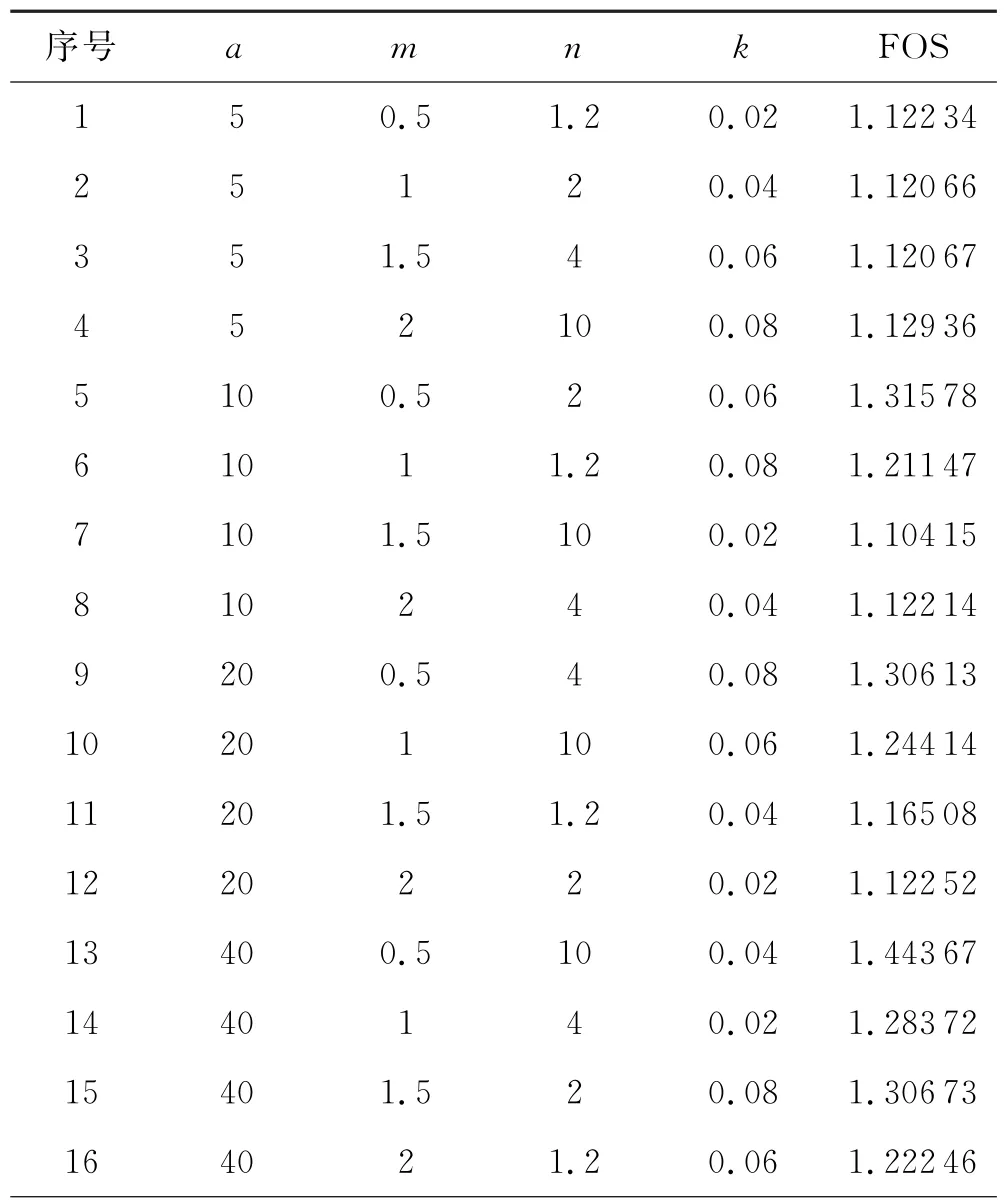
表3 有限元模拟正交实验结果

续表3 有限元模拟正交实验结果
由表3可见,参数m,n的极差较小,而参数a,k的极差较大,说明参数m,n对边坡稳定性的影响较小,而参数a,k对边坡稳定性的影响较大,由此可见,在进行边坡库水位骤降数值模拟中应该对参数a与k进行准确的测量,不同参数对边坡稳定性影响大小排序为参数a≥参数k≥参数m≥参数n.
4 结 论
1)库水位骤降下不同监测点孔压呈现先减小后不变的趋势,上部监测点的孔压降幅较下部监测点要小,孔压降幅与参数a,k呈负相关,而与参数m呈正相关.
2)库水位骤降情况下上部监测点与下部监测点存在两个变形阶段,即库水位骤降时间段内的位移快速上升阶段以及库水位骤降结束后的位移缓慢上升阶段,上部监测点的位移要大于下部监测点的位移.
3)参数a与参数k变动对安全系数的变幅影响较大,参数m与参数n对安全系数的变幅影响较小,参数a,m,k与安全系数呈正相关,而参数n与安全系数呈负相关.
4)对非饱和参数对边坡稳定性进行了正交实验敏感性分析,参数a,m,n,k的敏感性大小分别为参数a≥参数k≥参数m≥参数n.

