基于量纲分析的弧形闸门过流公式应用

于思雨 苏志伟 高玺炜 李晓英

(1.辽宁蒲石河抽水蓄能有限公司,辽宁 丹东 118216;2.青海民族大学 建筑工程学院,西宁 810000;3.河海大学 水利水电学院,南京 210098)

在水利工程设计及运行阶段,弧形闸门过闸流量的确定,关系到水利工程的投资与安全运行.目前较为常用的闸门过流公式如传统水力学公式、亨利公式、杜屿公式、日本土木学会公式、美国陆军工程兵团公式等[1-5],均由能量方程推导得出,这些公式虽然应用较为广泛,但是存在一些缺点.首先需要确定流量系数和淹没系数,这两项系数一般通过水工物理模型实验率定或水工物原型记录数据率定,鉴于弧形闸门自身结构原因,率定难度较大;其次在潜流比达到0.96及以上时,微小的淹没系数变化,将导致巨大的数据误差;另外,由于公式中均含有经验公式,不能广泛应用于一切实际水工建筑物中;最后由于水位-流量关系曲线属于非线性,为了提升精确度,在不同工况下均需进行多组试验,率定工作量非常大,以文献[6]为例,各工况下水位-流量关系曲线均包含6个左右的数据点,为使得拟合精确度达到要求,工况实验次数在30组以上,基于量纲分析进行过流公式推导,则可以有效地避免这些缺点.

1 量纲分析法

量纲分析作为建立数学模型的重要方法,在一些较为复杂的问题中,通常难以构建准确的数学方程或者模型,但可通过确定各个影响因子对研究目标的作用情况,进而确定研究问题中的函数关系式.

量纲分析一般步骤如下：

第1步：根据研究的问题,选择合理的物理研究量,用q1,q2,…,q m表示;

第2步：用物理学基本的7个量纲表达,q i表达为

第3步：设q1,q2,…,q m满足关系其中y j为待定,根据量纲齐次得到(i=1,2,…,n);

第4步：求解步骤3线性方程组,记A=(a ij)n,m,若矩阵A的秩rank(A)=r,A y=0的m-r个基本解可以表示y k=(y k1,y k2,…,y km)T(k=1,2,…,m-r);

第5步：根据步骤4矩阵A的解,得到研究问题的数学表达.

2 弧形闸门无量纲关系式

弧形闸门示意图如图1所示.

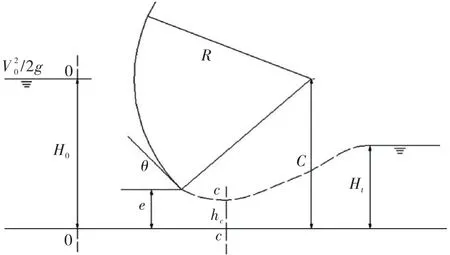
图1 弧形闸门示意图

弧形闸门过流公式一般基于能量公式,以闸前断面0-0及收缩断面c-c建立能量方程.

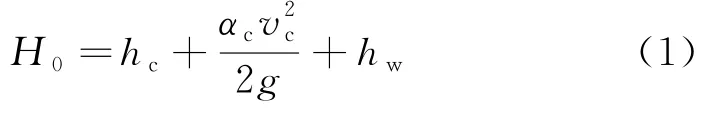
式中,H0为包含流速水头的闸前全水头;hc、vc为收缩断面的水深和流速;g为重力加速度;hw为0-0断面到c-c断面的水头损失.

由能量方程(1)整理可得闸门出流的水力计算公式[6]：

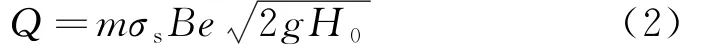
式中,m为流量系数;σs为淹没系数;B为闸门宽度;g为重力加速度;e为闸门开度;H0同上.由于弧形闸门的水力关系异常复杂(特别是在潜流比较大时),公式(2)特别难以率定,根据文献[7]的相关研究发现,率定的误差在正负20%区间.

将量纲分析应用于闸门过流计算率先由Chadwich和Morfett提出[8].对于弧形闸门而言,淹没出流条件下,单宽流量q,可假定为闸门开度e、重力加速度g、过闸前后能量差HE和绝对粘性系数μ的函数,则q和H E表达式为：

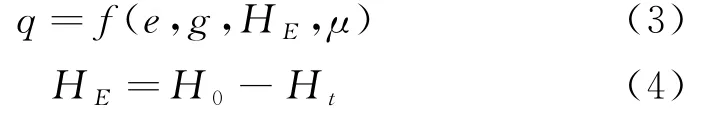
假定过闸流量具备以下形式：

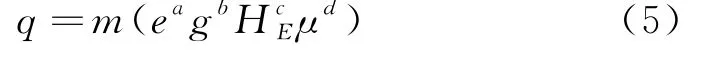
式中,a、b、c、d和m为常系数.

利用量纲分析可得：

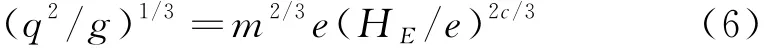
令K=(q2/g)1/3,i=m2/3,j=2c/3做变量替换可得无量纲关系式：

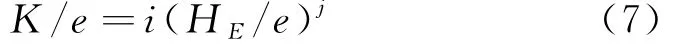
对于自由出流,公式(7)同样成立,此时下游水深H t设定为0.

3 弧形闸门过流公式拟定[9-10]

无量纲公式(7)在计算弧形闸门过流能力时不够直观,参数率定也不简明,本文在公式(7)的基础上,按水力学通用弧形闸门过流形式,推导以量纲分析法为原则的计算公式：

自由出流公式：

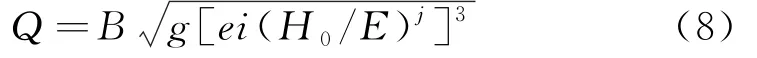
淹没出流公式：

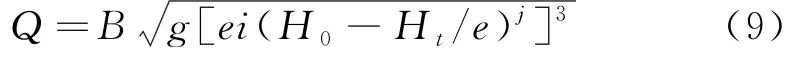
为了便于公式中参数的率定,对公式(7)两端进行对数变换：

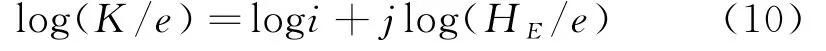
设变量y=log(K/e),x=log(H E/e),b=log(i),a=j,那么公式(10)变形为：上式为线性函数,通过实测运行数据可以方便的拟合出方程的斜率和截距,从而可求得i,j,便得到了闸门开度、流量、水头的关系式,其中：

4 实例应用

蒲石河抽水蓄能电站下水库引水坝共分19个坝段.共11个挡水坝段,由普通挡水坝段、门库挡水坝段、电梯井坝段、导流底孔坝段及引水坝段组成,其中4号～11号坝段为泄洪排沙闸坝段,下水库大坝左岸上坝公路与对外交通相接[11].

下水库设有7孔泄洪排沙闸,每孔设1扇弧形工作闸门,每孔净宽14 m,闸墩厚4 m,溢流前缘净宽为98 m,全长136 m.建基高程为36 m.采用开敞式泄洪方式,堰面采用WES幂曲线,堰顶高程48 m,堰上布置弧形工作闸门挡水,弧门前设一道检修平板门;在两边墩上游各设导流墙,导墙顶高程67.33 m,导墙高25.33 m,顶宽1 m.

准确率定弧形闸门过流能力,可为电站运行调度方案制定提供科学依据,拟采用现场实测数据进行弧形闸门公式率定.筛选辽宁蒲石河抽水蓄能电站2013年至2016年弧形闸门操作记录部分数据进行量纲公式拟合,由于电站运行以来未出现淹没出流状态,因而本文仅对自由出流公式进行率定,部分闸门操作数据见表1.

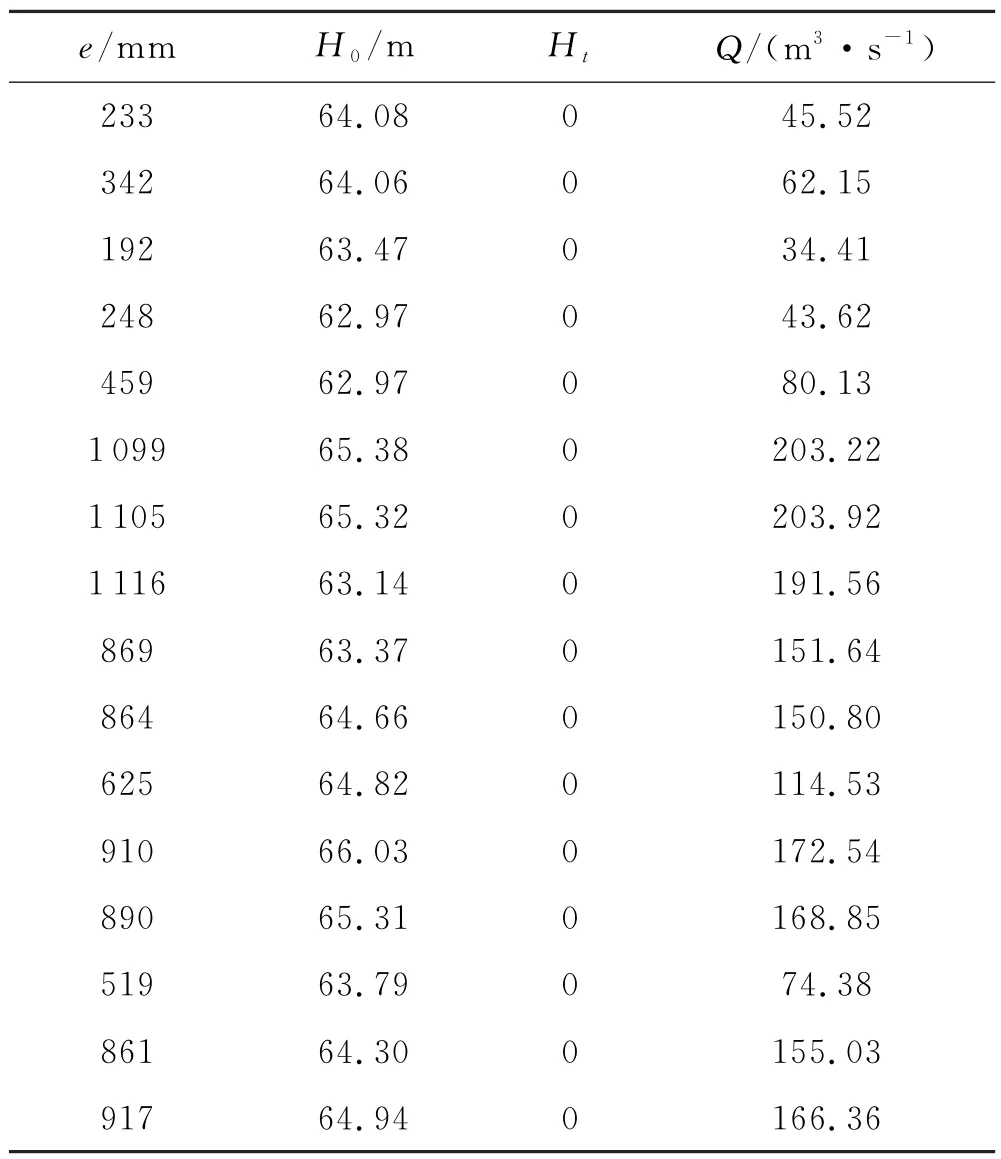
表1 弧形闸门率定数据参数

根据实测数据,以y=log(K/e),x=log(H E/e)为坐标,绘制数据点,并拟合弧形闸门过流关系曲线如图2所示,拟合关系曲线如式(13)所示.

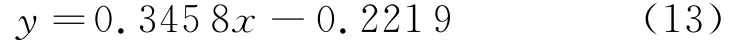
根据关系式(12)可得：i=10b=0.599 9,j=a=0.345 8.

将此带入到公式(8)即可得到弧形闸门自由出流的关系为：

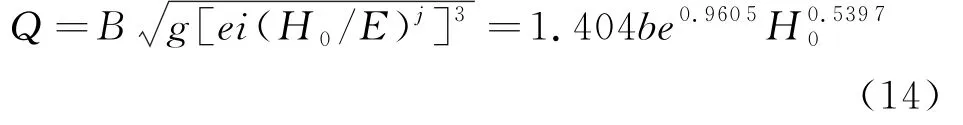
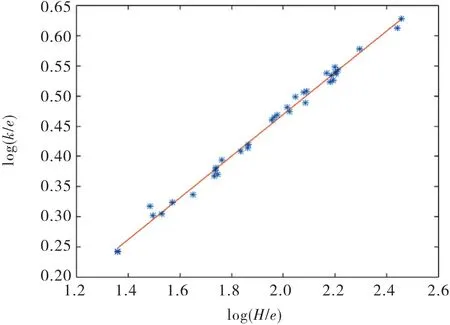
图2 量纲分析法弧形闸门过流公式率定曲线

为了检验量纲分析法得到的弧形闸门过流公式的准确性,同样随机选取2013至2016蒲石河电站实际操作记录数据作为检验数据,对拟合公式进行验证分析,所得结果见表2.

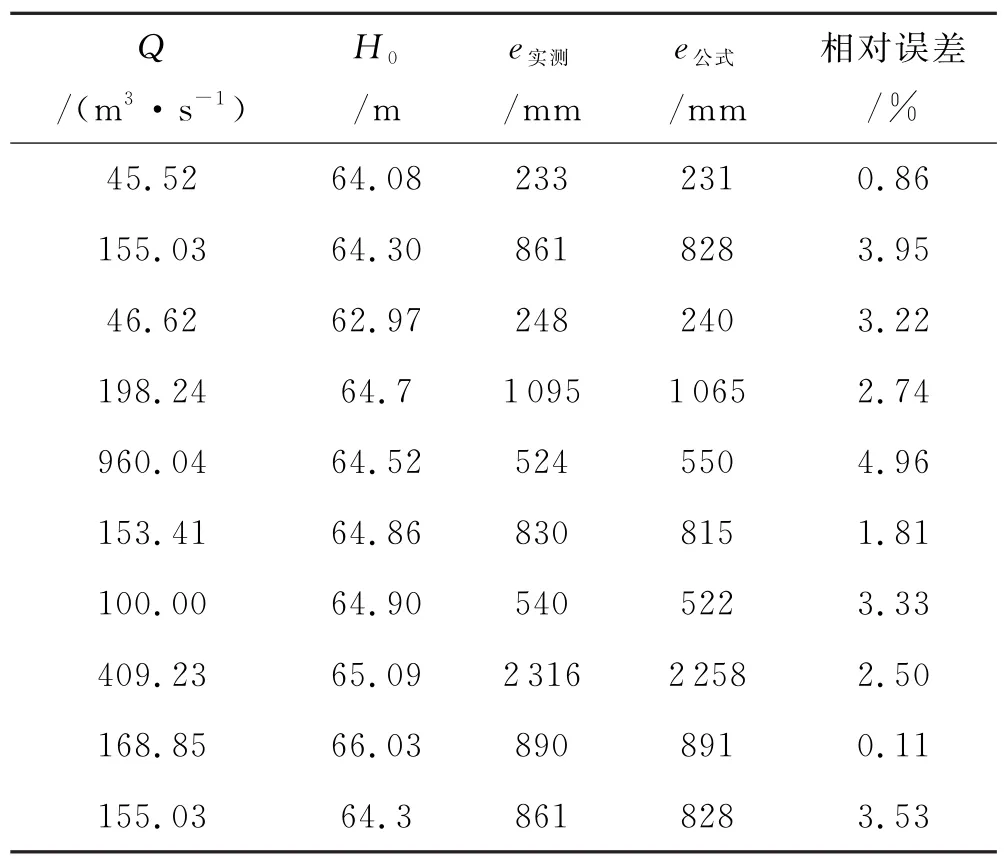
表2 率定公式检验表

由表2可见,拟合公式所得数据与实测数据之间,最大绝对相对误差为4.96%,最小绝对相对误差为0.11%,均在5%范围内,拟合公式计算结果理想,可用于指导实际闸门操作过程.

5 结 论

1)量纲分析法公式形式简明,公式率定过程简单快捷.对于水工物理模型弧形闸门过流公式率定过程,采用线性关系拟合公式,可以根据试验数据点的位置判定数据的合理性,提高试验精度;而常规方法如水力学公式、亨利公式、杜屿公式等,试验过程不易判定数据的合理性,因而精确度会受到很大的影响.

2)基于量纲分析的弧形闸门过流公式精度高,常规方法拟合的公式误差通常在20%区间内,本文构建的公式在实际应用中其误差在5%以内,另外基于量纲分析法的弧形闸门公式率定工作量与常规方法比要小很多.