中小型风电机组变桨距控制算法研究

陈广华，张 健，张坤婷，李梦凡

(1. 北京交通大学 机械与电子控制工程学院，北京 100044；2.中国科学院自动化研究所，北京 100190)

大规模风力发电对地理位置和环境的要求极高，造成了严重的弃风现象，相较而言中小型独立风

电机组因其具有较好的灵活性、方便单独安装等特点，可以增强风能利用率，有很大发展前景[1].

国内外学者研究表明，大型风电场的使用会严重影响气候变化，使得气温等环境因素发生巨大变化[2-3].通过美国风能协会研究可预测，到2020年中小型风电机组发电量将会占美国电力消耗的3%[4].由此可见，中小型风电机组有很大的发展潜力.为了更好地控制风电机组的发电稳定性与可靠性，国内外研究机构对风电机组控制方法进行了研究.文献[5]研究了机械折尾翼装置的控制，但是随着风电机组发电量的提升，调节效果明显下降.文献[6]研究实现了最大功率跟踪控制的方法，适用于额定转速以下的低风速控制.文献[5-6]所研究的控制方法多用于低风速、定桨距风机，当风速超过风机能稳定工作的额定风速时，不能起到很好的控制作用，会使机构由于过载而发生飞车等事故.为了使风电机组在高风速时有更好的可靠性和稳定性，对桨距角可变的风电机组进行控制变得至关重要.文献[7]通过控制器调节液压杆的位置来转动风机桨叶，实现了变桨距调节.文献[8]建立了风电机组模型，设计了PI控制器并选用适当的增益系数，实现了高风速状况下输出功率的稳定控制.文献[9-11]研究了变桨距PID控制器，以桨距角差值为输入，通过闭环控制实现转速的稳定控制.通过分析可知国内外对于变桨距控制器的研究集中于经典PID控制器，对于非线性、多变的风速状况时，该控制器的控制效果具有一定局限性，不能及时准确地作出响应.

针对上述问题，本文作者提出利用模糊PID变桨距控制的方法实现高风速状况下风电机组输出的稳定控制，充分利用模糊PID控制器在线调整参数的特点，对多变的风速状况有更强的适应性，能够实现较好的控制效果.

1 独立风电系统变桨距控制原理

1.1 变桨距控制理论依据

在独立风电机组变桨距控制系统中，以步进电机作为调整叶片桨距角的执行机构.如图1所示为独立风力发电系统，其中变桨距控制装置位于风机叶片根部，步进电机通过控制与叶片连接的转轴实现桨距角β的调节.

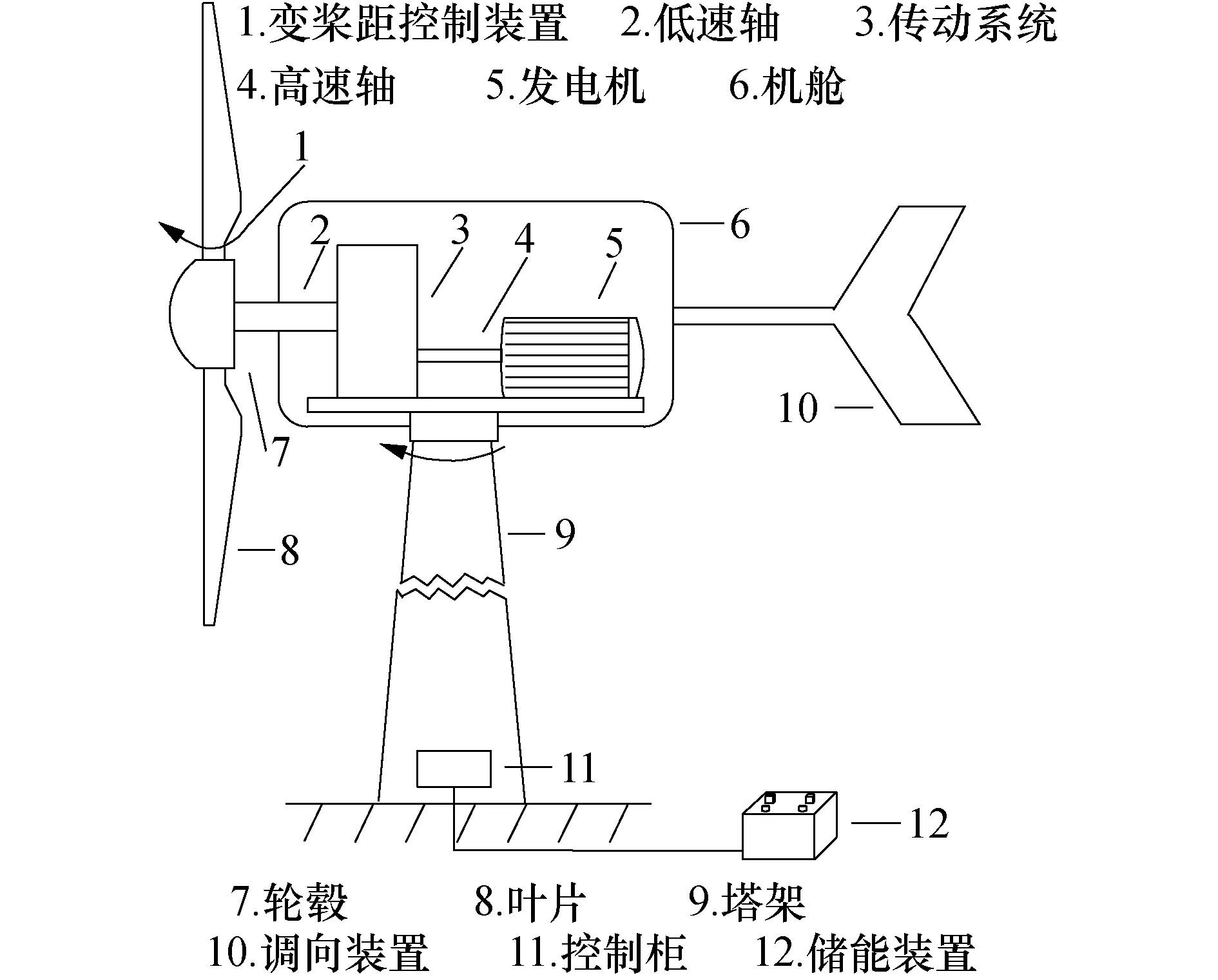
图1 独立风力发电系统Fig.1 Independent wind power generation system

在变桨距控制系统中，风能利用系数Cp是风电机从自然风能中吸取能量的大小程度，表示了风力发电机将风能转化成电能的转换效率[12].Cp是关于叶尖速比λ和桨距角β的非线性函数，即Cp=f(λ,β)，如图2所示为变桨距风电机组Cp与λ、β的关系曲线，由此可间接得到桨距角与转速之间的关系，为变桨距控制器设计提供理论依据.由图2可知：λ一定时，随着β增大Cp减小，即减少了风能的获取量.据此，在高风速状况下，调节β大小，改变风能的获取量，从而改变风轮转速，使其稳定在额定转速，风机输出稳定在额定功率，实现稳定发电[13-14].

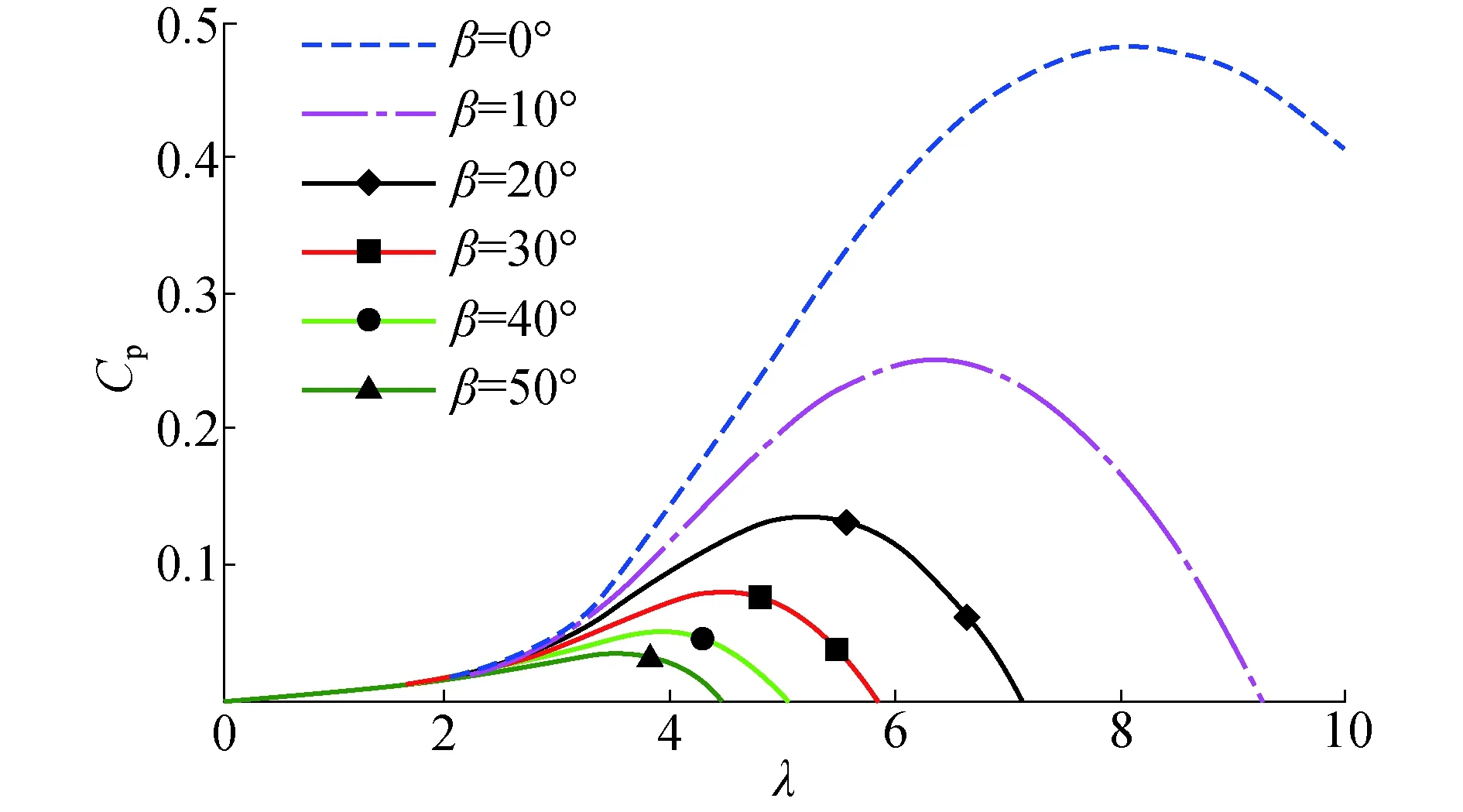
图2Cp=f(λ,β)关系曲线Fig.2 Relation curves of Cp=f(λ,β)

1.2 变桨距控制策略

中小型风电机组变桨距控制是通过控制步进电机转动，进而改变轮毂上桨叶桨距角大小的过程.基于步进电机的变桨距调节控制原理，见图3.

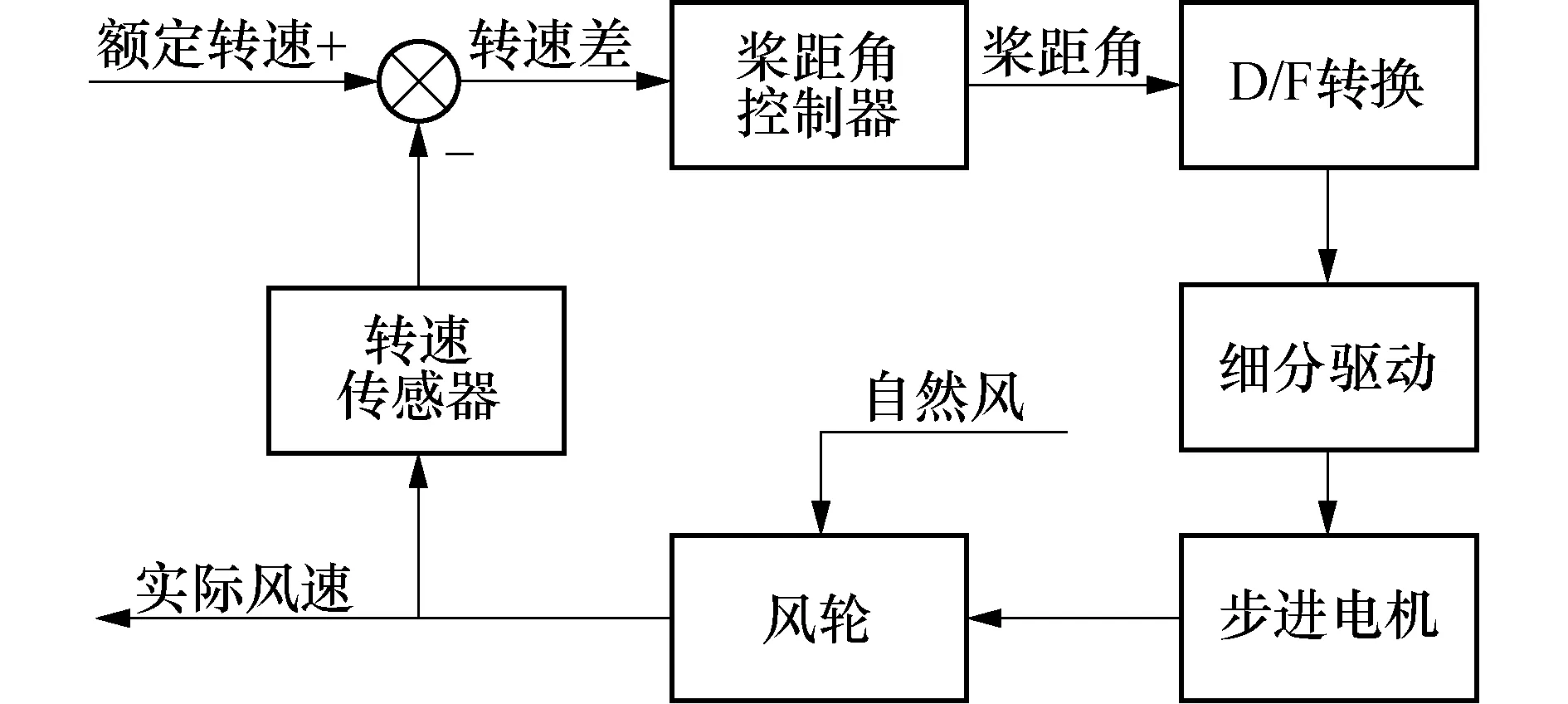
图3 步进电机变桨距调节原理Fig.3 Schematic diagram of stepper motor’s pitch adjustment

图3中桨距角控制器的输入为风轮额定转速与实际转速的差值，输出为桨距角，将输出信号转换为脉冲信号后，通过细分驱动器进一步精确控制变桨距步进电机的运行.变桨距步进电机带动桨叶转动，调整桨距角的大小，改变风能获取量，进而限制风机的转速，防止风速过大时风电机组过载.

2 变桨距控制算法研究与仿真

风电系统运行过程中，存在自然风随机性大的问题，造成整个系统具有强非线性，针对这种状况，变桨距控制采用模糊PID控制的方法，该方法具有的优势为：抗干扰性强，对于环境具有不确定性、随机性的问题有很大的适用性；容错能力较强，能够适应环境特征变化等状况[15].为确定模糊PID解决该变桨距问题品质的高低，在仿真分析时与经典PID控制进行比较.

如表1所示为整个经典PID和模糊PID控制器设计及仿真所需的风电机组系统仿真参数设置.

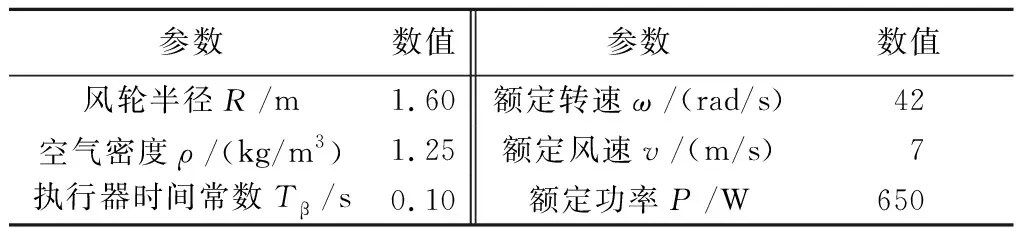
表1 风电机组系统仿真参数设置

2.1 经典PID变桨距控制器设计

依据高风速状况下风电机组工作状况，设计经典PID变桨距控制系统，如图4所示为PID变桨距控制器系统框图.

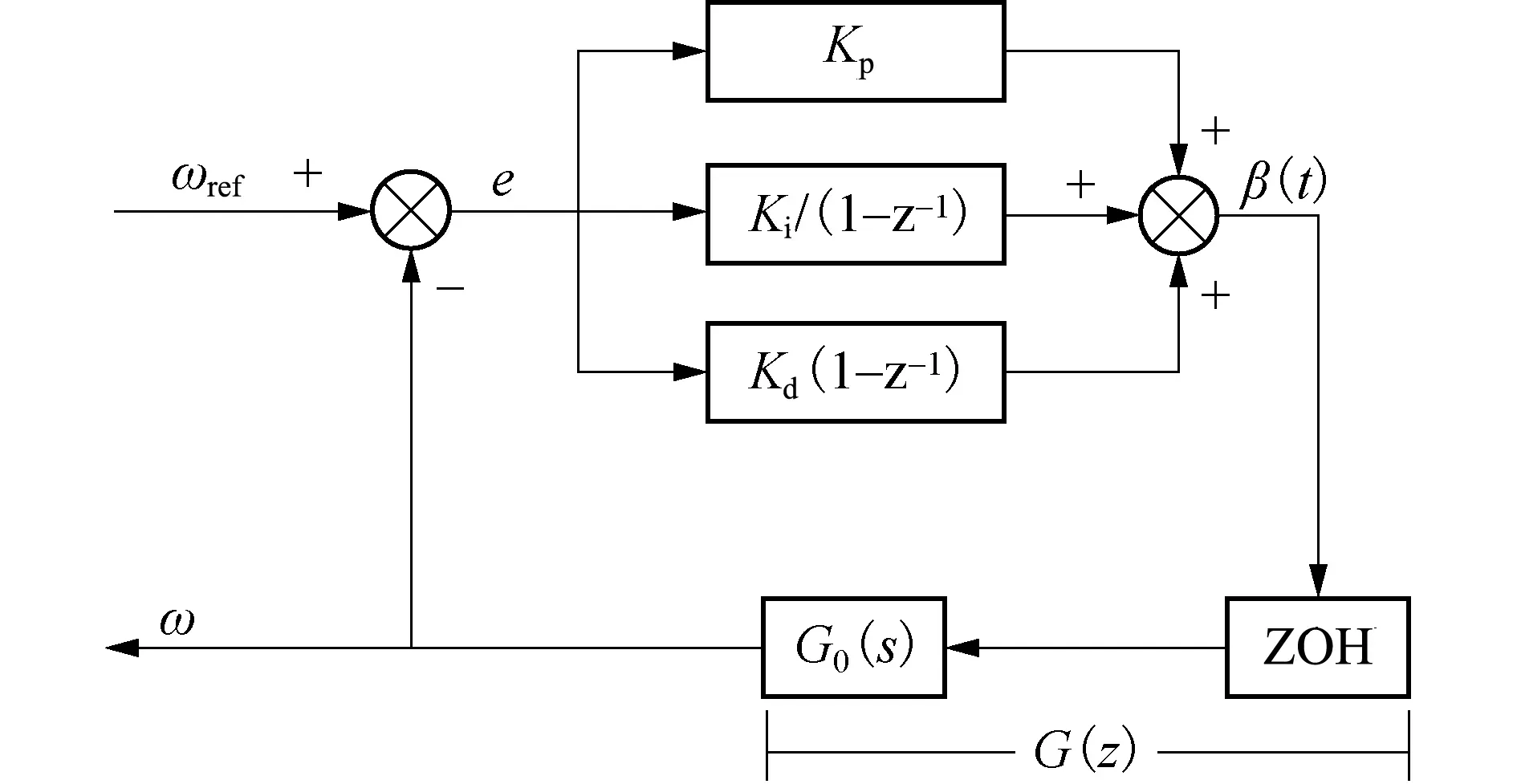
图4 PID变桨距控制器系统框图Fig.4 System block diagram of PID pitch controller

图4中，Kp、Ki、Kd分别为PID控制器的比例系数、积分系数、微分系数，PID控制器的输入e为风轮额定转速ωref和实际转速ω的差值，输出为调整后的桨距角β(t)，采样时间为0.1 s.在PID控制器的设计中，需要对Kp、Ki、Kd进行整定，选用临界比例度法进行参数整定,得到的整定结果为：Kp为0.3、Ki为0.5、Kd为0.01，整个控制器在进行控制过程中加入死区宽度，当输入误差小于0.6 rad/s时，不进行调节，这样阻止了桨距角变化频繁给系统带来过大的负担.

2.2 模糊PID变桨距控制器设计

根据风机工作状况以及现场供电要求，按照变桨距的具体实现过程，设计了专用的模糊PID变桨距控制器，PID的参数通过自动整定使得控制器在调节过程中有更好的适应性.如图5所示为模糊PID变桨距控制流程图.

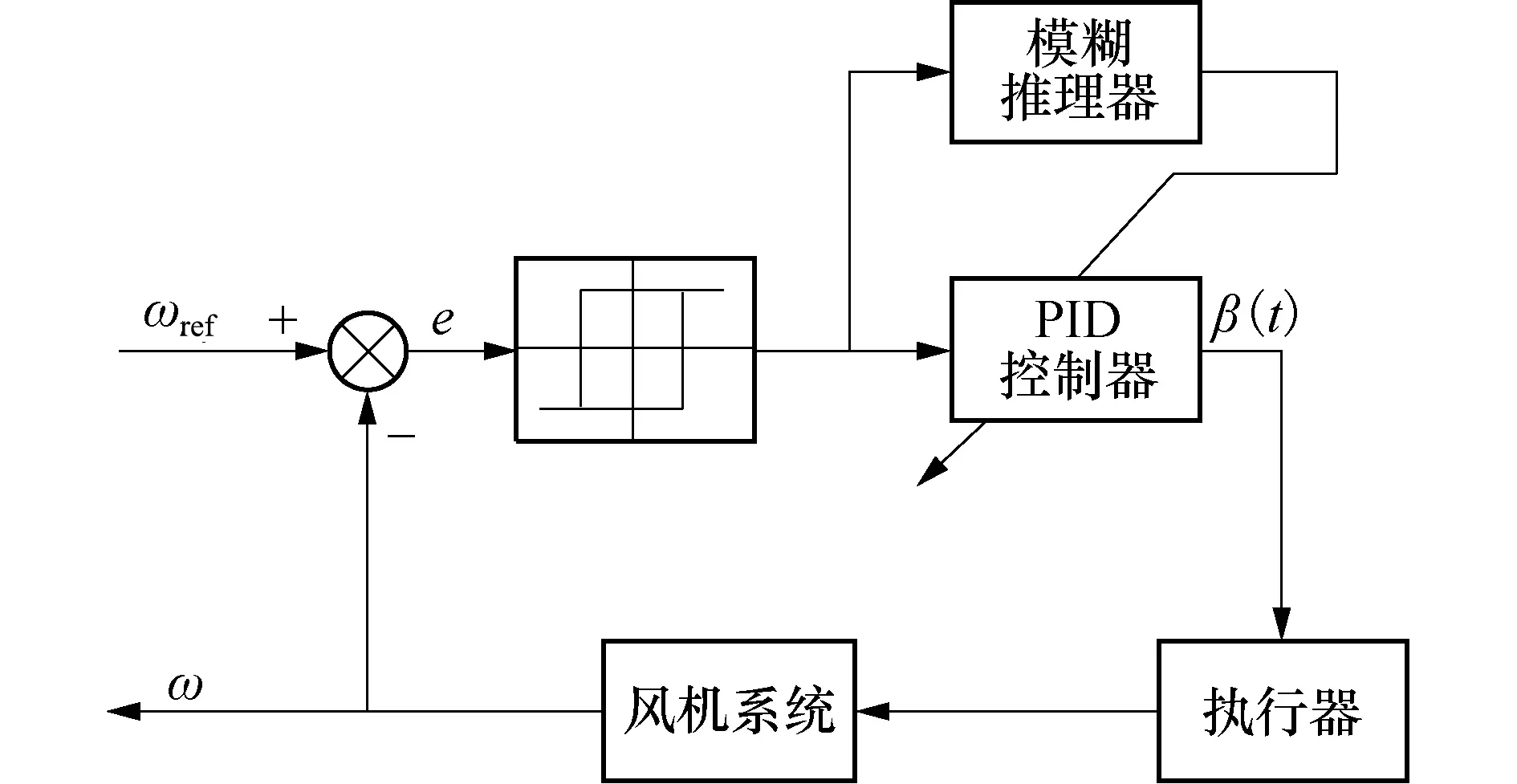
图5 模糊PID变桨距控制流程图Fig.5 Flow chart of fuzzy PID pitch control

由图5可知，整个变桨距控制过程中要想实现参数自整定，关键为模糊推理器的设计，结合实际的工作状况，设计的模糊推理器结构如图6所示.

图6 模糊推理器结构Fig.6 Fuzzy controller structure

根据系统要求，设计了该双输入3输出的推理器，由图6可知，模糊推理器的两个输入为转速偏差e和偏差变化率ec，多输入的控制器使得制定的模糊规则更加精确，将两个输入分别进行模糊化处理后用模糊子集E和EC表示；经过处理后，模糊推理器的输出为ΔKp、ΔKi、ΔKd，解模糊化后对PID的控制参数Kp、Ki、Kd进行精确计算，这样就完成了对PID控制参数的整定.整个模糊PID变桨距控制器设计过程的3个核心步骤为

1)模糊论域的选择.

对于输入输出变量需要确定其模糊论域，以额定风速为7 m/s的风速模型为例，通过测试分析可确定输入变量的基本论域：角速度偏差为[-30 30]rad/s，偏差变化率为[-600 600]；根据参数特点以及仿真结果选择ΔKp、ΔKi、ΔKd的基本论域，采用临界比例度法整定，初次设定Kp为0.3，Ki为0.5，Kd为0.01，之后通过自整定进行调节，ΔKp的基本论域为[0 0.1]，ΔKi的基本论域为[0 0.2]，ΔKd的基本论域为[0 0.003].

输入端e和ec的模糊论域为：Ue=Uec={-6,-4,-2,0,2,4,6}，输入模糊子集语言变量为{负大，负中，负小，零，正小，正中，正大}，定义为{NB,NM,NS,Z,PS,PM,PB}.

输出端ΔKp、ΔKi、ΔKd的模糊论域为：UΔkp=UΔki=UΔkd={0,2,4,6,8,10}，输出模糊子集语言变量为{零，小，中小，中，中大，大}，定义为{Z,S,MS,M,ML,L}.

2) 隶属度函数的确定.

在该变桨距控制器中，为了使风电机组稳定的工作，需要实现快速调节，对比常用的隶属度函数，三角形隶属度函数具有计算简单、速度更快的特点，能够满足要求，因此控制器的输入输出选用该隶属度函数.根据论域范围及合理性，2个输入变量都归为7个子集,对应的函数拐点为：[-8 -6 -4]、[-6 -4 -2]、[-4 -2 0]、[-2 0 2]、[0 2 4]、[2 4 6]、[4 6 8].按照相同的原则，将3个输出变量划分为6个子集，对应的函数拐点为：[-2 0 2]、[0 2 4]、[2 4 6]、[4 6 8]、[6 8 10]、[8 10 12].

3)模糊规则的制定.

在实现变桨距调节控制过程，要想通过输入量的变化确定输出量，必须制定编写合理的模糊规则.在该模糊控制器中，由2个输入量e、ec按照一定规则来调节ΔKp、ΔKi、ΔKd3个输出变量的值，进而完成对Kp、Ki、Kd数值的调节.要确定模糊规则，需要依据控制系统中各环节Kp、Ki、Kd对系统输出的影响以及专家经验来制定，如表2所示为ΔKp、ΔKi、ΔKd的模糊规则.

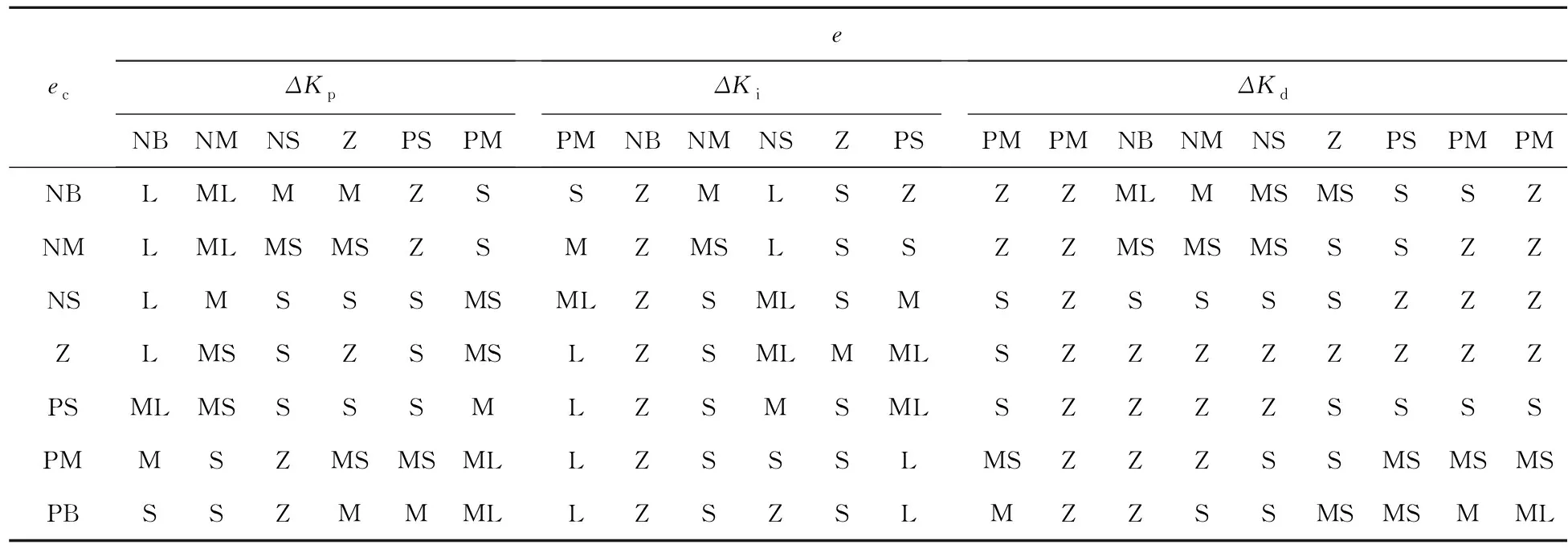
表2 模糊规则

3 仿真分析实验

通过建立渐变风速模型和阶跃风速模型进行经典PID和模糊PID变桨距控制器的仿真对比分析，进而验证高风速状况下不同控制方法稳定性输出效果的好坏.

3.1 渐变风速模型仿真分析

如图7所示为建立的渐变风速模型.

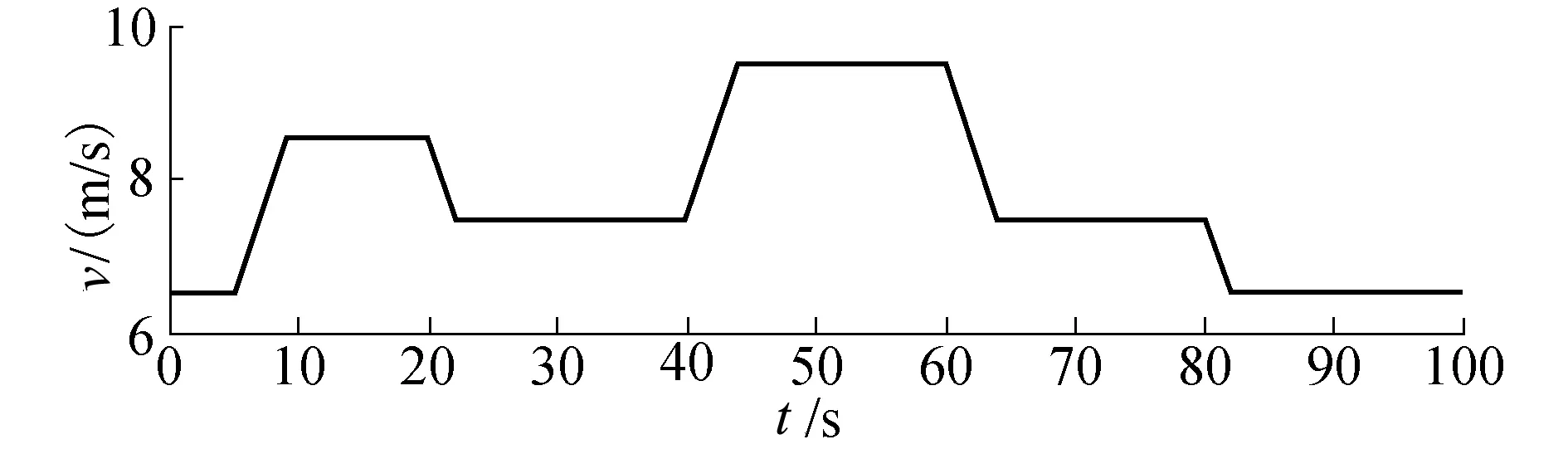
图7 渐变风速模型Fig.7 Simulation model of gradient wind

通过建立的渐变风速模型，对经典PID与模糊PID变桨距控制器分别进行仿真实验，通过变桨距控制器风轮角速度ω的调节变化过程可以比较控制器的调节效果.如图8所示为风轮角速度调节对比曲线.

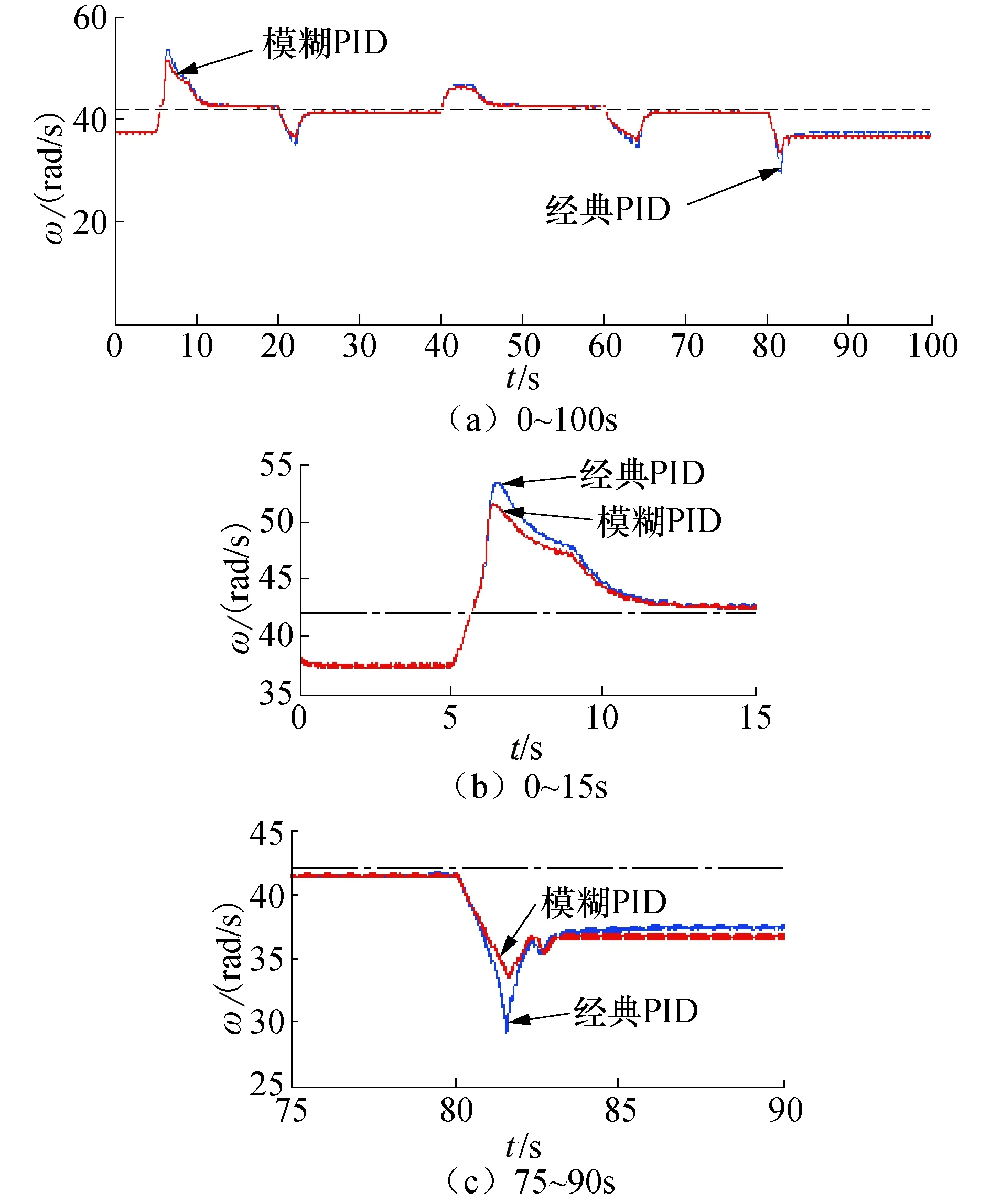
图8 渐变风速时风轮角速度调节对比曲线Fig.8 Contrast curves of wind wheel’sangular speed adjustment at gradient wind speed

整个渐变风速模型中，有5次的加减速变化，因此在控制器作用下，经历了5次的调节过程，通过仿真后得到风轮角速度的调节过程，在5～82 s时间段内，风速有5次的加减速过程，且风速大小处于额定风速之上，通过控制器调节桨距角，使风轮角速度稳定在额定转速42 rad/s.

如表3所示为经典PID和模糊PID两种控制器调节过程中角速度的最大超调量和调节时间统计表.通过仿真分析可知，渐变风速模型作用下，在超过额定风速时，模糊PID和经典PID两种控制算法都能调整桨距角将风轮转速控制在额定值42rad/s，实现了转速的稳定性控制，但模糊PID控制的最大超调量比经典PID控制下降了4%，调整时间下降了0.2 s.

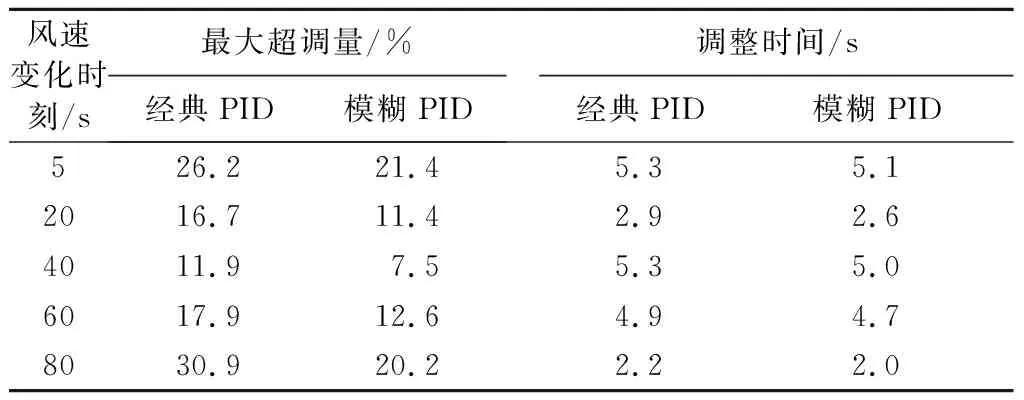
表3 渐变风速时数值对比

3.2 阶跃风速模型仿真分析

如图9所示为建立的阶跃风速模型.

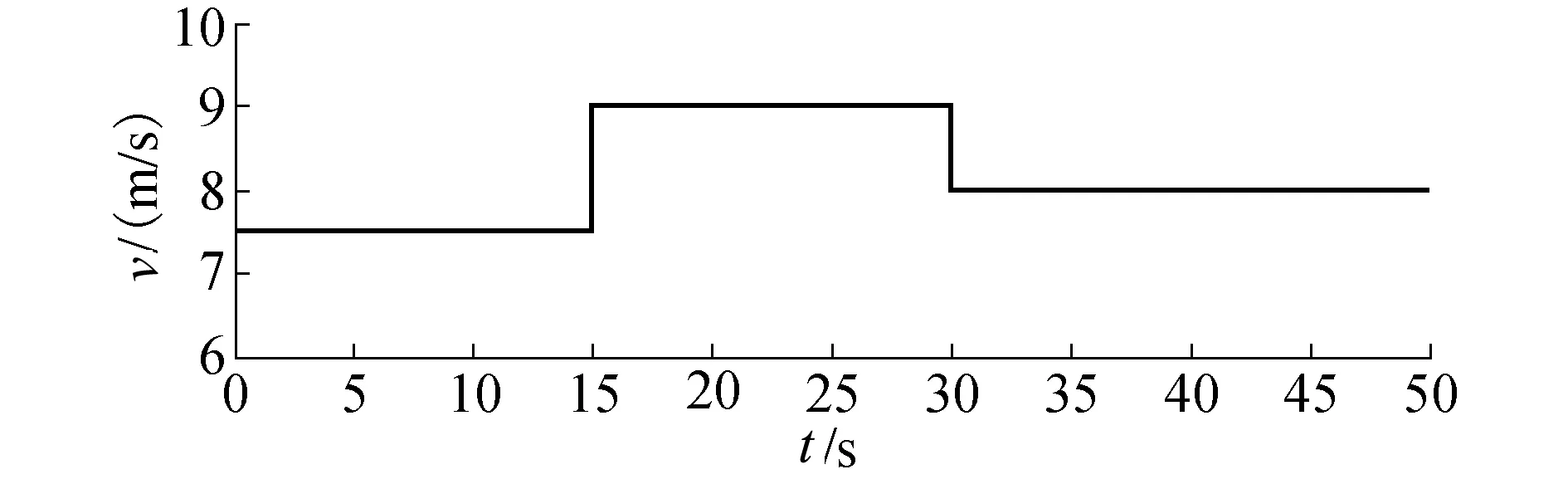
图9 阶跃风速模型Fig.9 Simulation model of step wind speed

通过建立的阶跃风速模型，对经典PID与模糊PID变桨距控制器分别进行仿真实验，通过变桨距控制器风轮角速度ω的调节变化过程可以比较控制器的调节效果.风轮角速度调节对比曲线见图10.

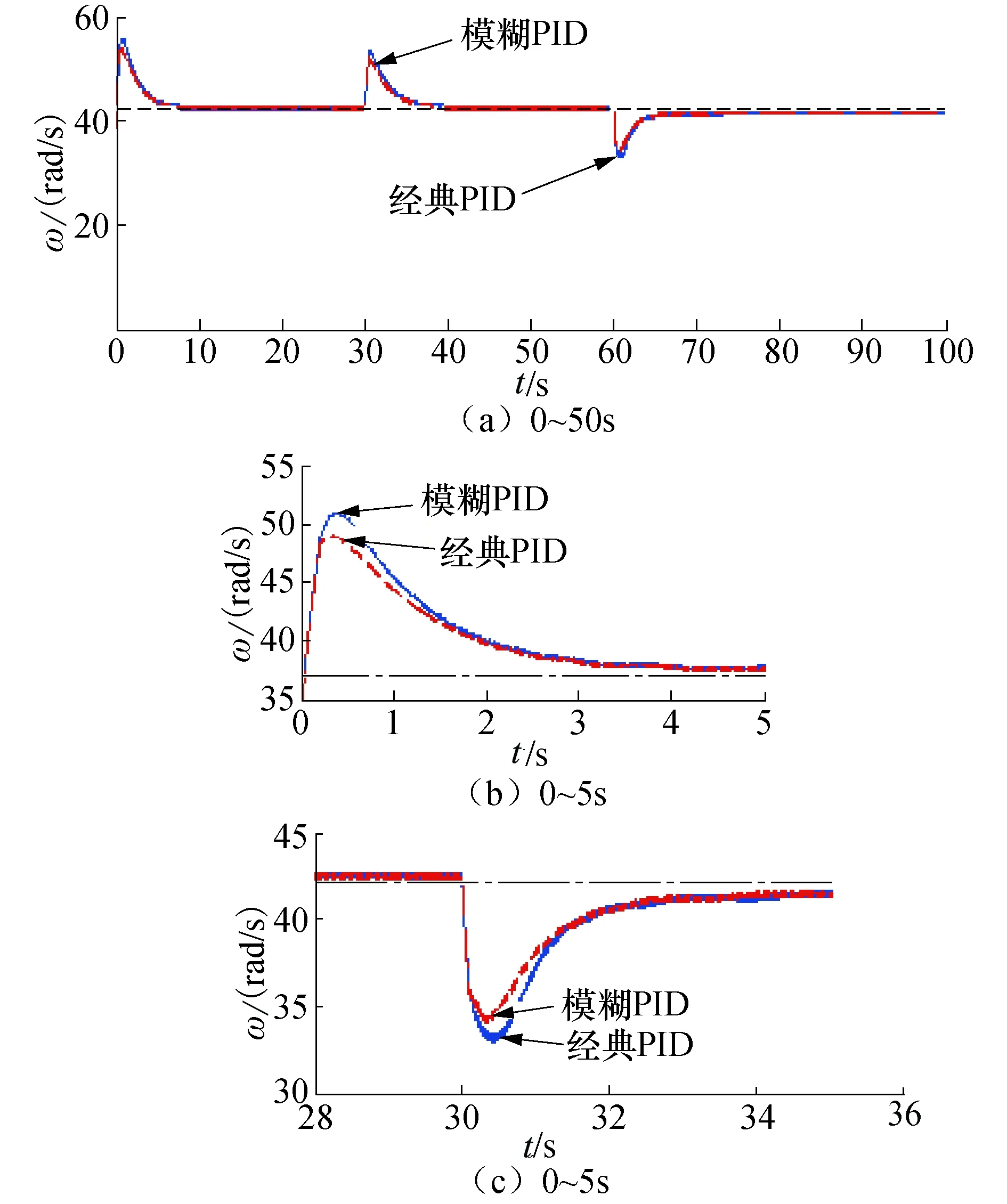
图10 阶跃风速时风轮角速度调节对比曲线Fig.10 Contrast curves of wind wheel’s angular speed adjustment at step wind speed

整个阶跃风速模型中，风速都大于额定风速，因此从开始变桨距控制器便会进行调节作用，在风速发生突变的时间点 ，通过变桨距控制器调节桨距角，使得角速度能够稳定在额定转速42 rad/s.统计两种控制器在整个调节过程中风轮角速度的最大超调量和调整时间，如表4所示.

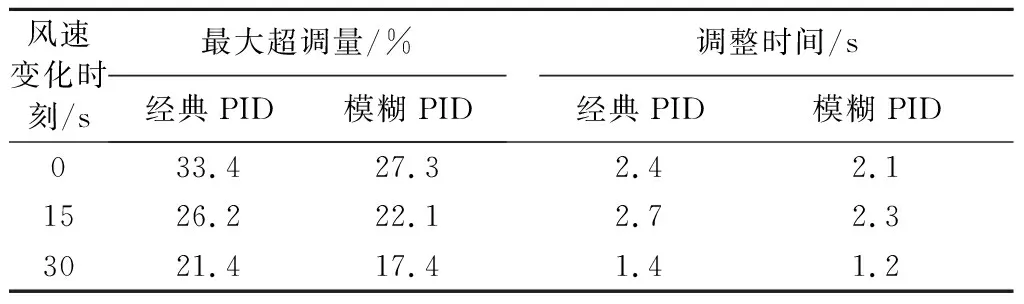
表4 阶跃风速时数值对比

通过仿真分析可知，阶跃风速模型作用下，在超过额定风速时，模糊PID和经典PID两种控制算法同样都能调整桨距角将风轮转速控制在额定值42 rad/s，实现了转速的稳定性控制，但模糊PID控制的最大超调量比经典PID控制下降了4%，调整时间下降了0.2 s.

整个仿真实验中，分别以渐变风速模型和阶跃风速模型进行控制器调节效果对比，通过对仿真过程中风轮角速度超调量和调节时间的统计可知：采用模糊PID控制使系统响应更加迅速、振荡更小，能够更快速地趋于稳定，比经典PID控制具有更大的优势.

4 现场测试分析

为了测试模糊PID变桨距控制器的实际效果，在风机现场进行车载实验，将整套风电机组系统安装在汽车上，通过汽车的行驶速度来改变风速，测试不同风速下变桨距控制系统调节效果的好坏，在整个过程中：风机转速由霍尔转速传感器获得；风电系统的输出电流由电流传感器测得、电压由电压传感器测得；风电机组的输出功率由测得的电流和电压计算得到.测试得到转速以及功率信号以细致地分析该系统的调节能力.

整个机组的测试硬件组装如图11所示，车载测试系统如图12所示.

图11 测试硬件组装Fig.11 Testing hardware assembly

图12 车载测试系统Fig.12 Vehicle test system

车载测试过程中，选用的风机桨叶直径为2 m，风轮额定转速为720 r/min，额定功率为300 W，额定风速为8 m/s.测试过程中统计的风机数据结果见表5.

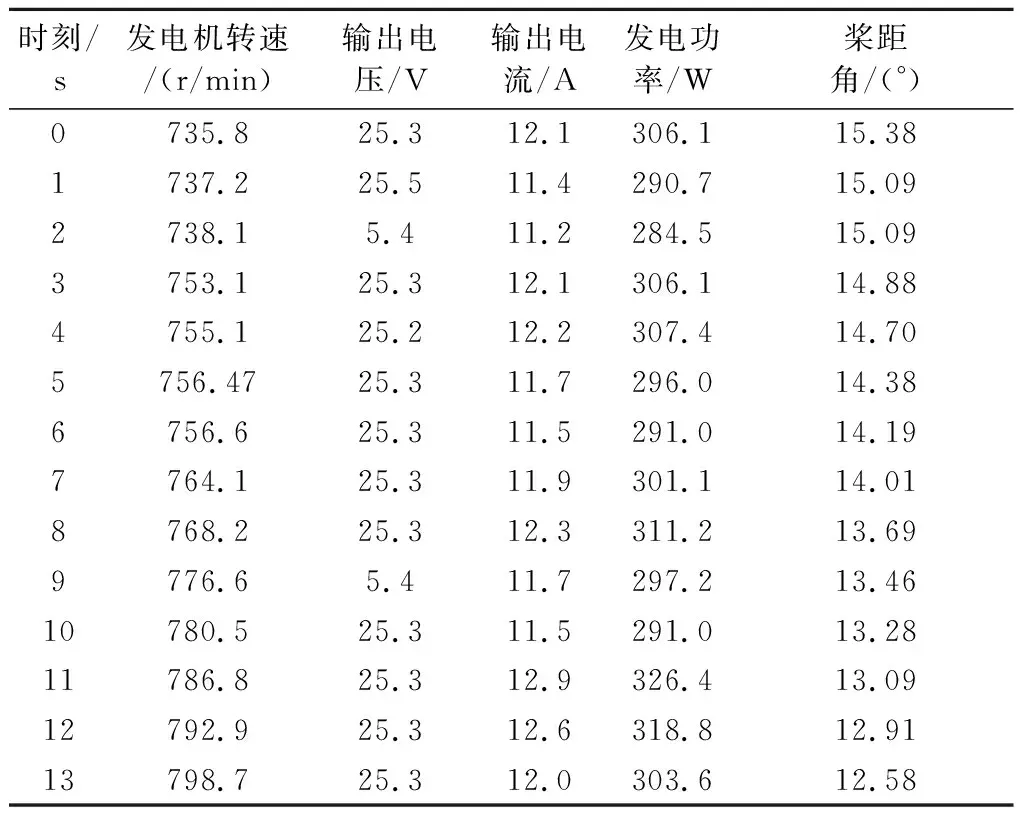
表5 测试数据统计

由表5可知：在高风速状况下，当转速和功率超过额定值时，变桨距控制器发挥作用，调节桨距角，减少风能的获取，使得转速和功率稳定在额定范围内，保证了输出的稳定控制.

5 结论

高风速状况下，为保证中小型风力发电机组输出稳定，设计了模糊PID变桨距控制器，完成风电机组运行控制.通过仿真实验及车载测试结果可得：

1)在两种不同风速模型下，对模糊PID和经典PID变桨距控制器进行仿真对比实验，由仿真结果可知，模糊PID控制的最大超调量比经典PID控制下降了4%，调整时间下降了0.2 s，模糊PID控制使系统响应更加迅速、振荡更小，能够更快速地趋于稳定，比经典PID控制具有更大的优势.

2)通过车载测试采集的数据分析可知，在整个变桨距调节过程中，可以将风轮转速和输出功率稳定在额定范围内，能够满足现场实际应用要求.