对穿锚杆锚固参数对支护体支护效果影响

韩龙飞,高华光

(河南理工大学 资源环境学院，河南 焦作 454000)

煤炭在我国能源消费结构中占75%以上，而且是重要的工业原料，从中提取的200多种产品是国家经济建设和人民生活所必需的[1].所以煤炭企业的安全、高效生产是事关国计民生的大事[2-3].而对于采煤地下交通系统而言，存在大量的斜交巷道[4]，这些巷道在交岔点附近空间较大，地应力相对集中，而此处抵抗地应力的岩(煤)壁相对较薄，由此形成了对交岔点处岩(煤)壁极为不利的力学环境[5]，往往在“牛鼻子”处会产生劈裂破坏或出现大变形，影响此处正常的采煤作业[61].由此针对较薄的岩(煤)壁的情况，人们提出了一种对穿锚杆(索)支护系统，该系统的核心是运用贯通岩(煤)壁的锚杆(索)系统对薄岩(煤)壁进行双向等同加固[7]，使加固后复合体能够有机地形成一个整体，从而力学性质更加均匀[8].对于对穿锚杆(索)支护系统，国内外的研究并不多见，而国内仅有少数人在对交岔点的“牛鼻子”进行加固时，曾运用过该方法，但并未对由此形成的复合受载体系进行系统研究.对于对穿锚固体中的锚固参数的研究虽然比较少，但是对于深部巷道的围岩变形问题[9]，前人已经根据实践工程得出很多研究成果，并且人们普遍认为锚固参数对支护效果有很大的影响[10].张合超与吴浩源[11]就通过FLAC3D进行模拟，将慈林山9103巷道的支护参数进行优化设计，使得支护成本明显降低.康红普[12]系统地分析了锚杆预应力、锚杆长度、锚杆支护密度、锚杆安装角度对锚杆预应力引起的应力场的影响.李金泉、刘少伟、张辉[13]等同样利用FLAC3D进行了数值模拟，模拟显示锚网喷联合支护方式对巷道的变形以及破坏都能起到抑制作用，可以很大程度上减小巷道围岩的变形量.

对穿锚杆支护效果以及锚杆支护参数尚没有一个系统的研究，本文针对对穿锚杆的参数包括锚杆直径、数量，利用FLAC3D软件对巷道间煤柱单元体进行数值模拟分析研究，结合室内相似试验，通过对对穿锚锚固体的峰后力学特性进行研究，分析其峰后强度提升的来源，为研究对穿锚杆锚固参数对支护体的支护杆效果提供更准确的理论基础.

1 相似试验设计以及模型的建立

1.1 相似试验

为了更准确地模拟出实际巷道的受力变形情况，选择相似试验作为研究手段之一.在模型的尺寸上，选择巷道单元体作为研究对象，模型尺寸为200 mm×150 mm×200 mm.模型的制作使用石膏、水，水膏比例为0.6∶1.制作时先称量好各材料所需量，将石膏粉快速倒入装水的桶内，其间搅拌机需要随之进行均匀的搅拌.搅拌均匀后倒入模具内，3天后脱模，在室内阴凉干燥处养护80天，每周将石膏块顺时针翻转一次.试验设备采用EHC-3100微机控制电液伺服万能机测控系统，对试件进行过载试验.石膏试件加载过程中锚杆施加位置及施加方法如图1.

图1 16根锚杆支护受载图

锚杆密度即锚杆数量试验方案为3种：分别是9，16,25根；锚杆直径方案有3种：锚杆直径分别为2，4，6 mm.在考虑锚杆直径3种方案时，锚杆密度均使用16根均匀分布.锚杆密度使用均匀布设，分3种方案进行试验，方案一使用9 根锚杆进行锚固，方案二使用16 根锚杆进行锚固，方案三使用25 根锚杆进行锚固.由于在考虑同一参数对支护体的影响时，需要控制其他变量，所以在考虑锚杆密度时，其锚杆直径均为4 mm.

1.2 数值模型的建立

针对深部煤炭利用沿空留巷的回采方式，巷道间预留煤柱符合双向应力状态，模型建立时应进行条件的约束.采用FLAC3D软件进行数值模拟分析，由于煤岩体的应力应变特征为峰后强度急剧下降，直至煤岩体完全破坏.所以，FLAC3D中的本构模型选用的是应变软化摩尔-库伦塑性模型，同样建立200 mm×150 mm×200 mm的立方体模型(如图2)，以模拟巷道间的预留煤柱.在200 mm×150 mm的两个侧面，约束其x方向位移的边界即为约束边界.在底面添加参数远大于受力模型的底板，以限制模型的z方向位移.顶板与底板参数相同，但顶板为施加竖直面力的传递体，其受的面力如图2的顶板中，有施加竖向的位移矢量箭头，通过顶面的恒定的竖向位移-1×10-6m/s，进而施加竖向应力为0.05 kN/s.数值模拟中用liner单元模拟托盘单元，对穿锚杆由于是无粘结锚杆，靠锚固体两侧的托盘单元进行连接，充当受力锚固段.这里将liner单元与锚杆cable单元之间的连接用刚性链接，可以模拟实际中的托盘单元[14].

图2 模拟模型边界示意图

基于巷道煤岩情况，FLAC3D中模型的参数如表1所示.

表1 模拟参数表

本构模型中应变软化模型的table值见表2.

表2 本构模型table值

2 对穿锚杆支护参数的分析研究

2.1 对穿锚杆密度对支护体的强化特征

施加锚杆后，其峰值强度以及峰后强度得到明显的提升.如图3，对应力应变曲线进行简化处理后，其锚固体峰值强度提升相对于峰后强度而言，对巷道支护的作用更大.而对于这部分峰后强度的提升，必定是锚杆所带来的.

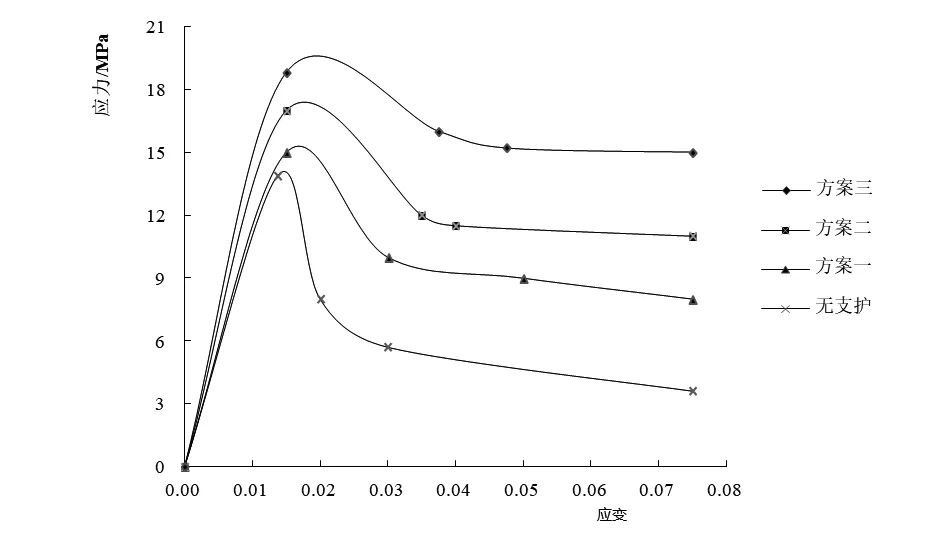
图3 锚杆密度对锚固体应力应变曲线的影响

由摩尔库伦准则可知，锚固体内聚力公式为

(1)

式(1)中：c为内聚力，Φ为内摩擦角，σ1为最大主应力，σ3为最小主应力.

由于峰后锚固体为复合体，需要作为复合体进行考虑其受力状态.所以锚固体已经成为一个整体，从结构力学角度分析，在这个整体中，锚固体不再受到最小主应力σ3，所以其值为0，σ1为其顶面所受应力.其峰后的等效内摩擦角[15](峰后无实际的内摩擦角，但是其强度特征符合库伦强度准则，即等效内摩擦角为峰后的锚固体共同提供克服内部滑动摩擦所需要的力的一种摩擦特征)改变较小，所以内摩擦角Φ的改变对锚固体强度的影响较小，假设其峰后等效内摩擦角不变[16]，均和峰前的一样为35°.这在技术上是可行的，理论中仍然可以假设.则峰后等效内聚力(峰后锚固体为一个整体，其内聚力无法根据相应的理论进行测算，即峰后等效内聚力为峰后锚固体作为整体共同抵抗剪切破坏的复合力)公式变为

c′=0.26σ1.

(2)

顶面应力σ1即为应力应变曲线中应力，求出其峰后等效内聚力曲线，根据公式发现由等效内聚力提供的增长量远远小于其强度的提升量.即等效内聚力增量与峰后强度增量之间有一个扩大系数，以方案三为例，通过线性关系分析，发现锚固体等效内聚力增量ci与其峰后强度增量si之间符合如下关系式：

ci=3.599si+1.458 2.

(3)

从式(3)中可以看出，锚固体等效内聚力增量与锚固体峰后强度增量呈线性正相关关系，且其相关性系数达到0.931 7，如图4，说明相关性较好.即锚固体等效内聚力公式符合后续计算，且该公式对锚固体峰后强度特征的确定有一定的意义.

锚固体的等效弹性模量(锚固体作为锚杆与岩体的共同体，其共同提供的弹性模量)相较于无支护都有明显的改善，其弹性模量即应力应变曲线峰值前的曲线斜率，经计算得到方案一等效弹性模量为1.026 GPa，方案二为1.13 GPa，方案三为1.25 Gpa，虽然锚固体的弹性模量并没有较大的改变，但是对锚固后模型的峰值强度有一定幅度的改善，相较于无支护模型，方案一的峰值强度达到15.4 MPa，方案二峰值强度达到17 MPa，方案三的峰值强度达到18.8 MPa.锚杆密度上升以后，就锚固体弹性模量而言，其峰值强度的提升，并没有太大意义.而峰后由于锚杆作用，锚固体侧向膨胀受阻，致使其锚固体作为整体受力，峰后等效内聚力增量远大于峰前，且其值与峰后强度之间呈正相关关系.

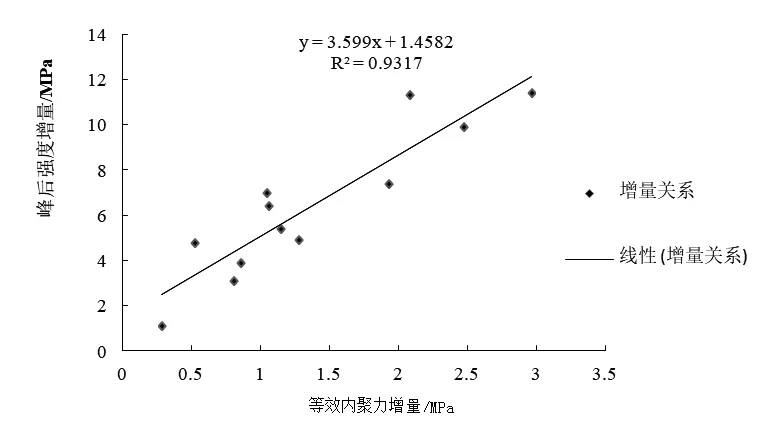
图4 等效内聚力增量与峰后承载力增量关系

除此之外，锚杆处于不同位置其作用大小也不一样，中间部分锚杆在受力过程中起到了最大的作用，以方案二为例，锚杆受力最大的均为锚杆处于模型中间部位的那部分，说明锚杆处于中间对于锚固体峰后强度的提升有较大的作用.而处于底部锚杆轴力值明显要小于锚固体中部与上部，中间部位的锚杆最大轴力是底部锚杆最大轴力的三倍，中间部位锚杆作用也将远大于底部锚杆.

锚杆密度增加，其峰后强度也在增加.且密度越大，峰后强度增幅越大.从另一方面来讲，锚固体的峰后强度与锚杆数量是有关系的.并且锚杆密度增加后，锚固体的峰后强度明显得到更大的提升，且能够使锚固体在峰值后仍保持一定的强度进行承载作用，这对于巷道的煤岩承载力而言，意义重大.因为实际中巷道由于地应力作用，煤岩大多数处于峰后阶段，锚杆的施加能够使得巷道中岩(煤)体继续达到承载要求，保证煤巷的安全.考虑到成本、经济效益，只要锚固体的强度能够达到要求，尽可能在保证其整体承载能力下，增加中间的锚杆数量，带来的支护效果更好.

2.2 对穿锚杆直径对支护的强化特征

巷道锚固支护中，对于锚杆的使用，通常不会轻易改变锚杆直径这一参数，但针对不同的支护条件，在需要改变锚杆直径时，考虑到锚杆锚固力与锚杆杆件破断力相等[10]，则锚杆直径为：

(4)

式(4)中：d—锚杆直径，m；Q—锚杆锚固力，kN；σt—锚杆杆体的抗拉强度，MPa.

室内试验以及数值模拟过程中，方案一为锚杆直径2 mm，方案二为锚杆直径4 mm，方案三为锚杆直径6 mm.模拟结果发现锚杆直径改变后，其锚固体的峰后强度有明显变化，从峰后曲线来看，当锚杆直径为2 mm时，锚固体峰后强度稳定至10 MPa；而当锚杆直径提升至4 mm，锚固体峰后强度稳定至12 MPa；锚杆直径继续提升6 mm，但峰后强度仍稳定至12 MPa.这是因为当锚杆直径为2 mm时，锚杆在峰后被压断，导致峰后强度下降较多.而锚杆直径提升至4 mm以后，锚杆力学性质能力大幅提升，不会再被压断，导致锚杆直径继续提升后，其峰后强度提升并不明显.而峰值强度由于锚杆直径的提升，在前期实体被Z方向挤压时，锚杆的Z向抗变形能力提高，影响了其峰值强度，如图5不同锚杆直径下锚固体应力应变曲线.锚杆直径改变后，直接影响锚固体的峰后强度.即说明锚杆直径的改变对锚固体的峰后强度的影响较大，但当直径超过一定值后，其Y向抗挤压能力已经不会使其破断.此时，若继续增加锚杆直径，其峰后强度提升不够明显.

另外，从锚固体受力后的Y向位移对比来看，锚杆直径增大后，锚固体在应力增大后的Y向位移量有所减小.由于模型尺寸较小，减少的量有限，如图6，增加锚杆直径后，锚固体Y向位移量及总位移量明显减小.但当锚杆直径超过4 mm后，锚固体位移量减小的幅度开始降低，这说明此时再增加锚杆直径，作用较小.

图5 不同锚杆直径下锚固体应力应变曲线

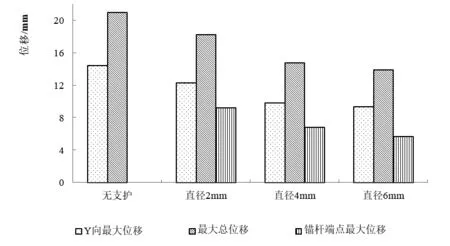
图6 锚杆直径对锚固体位移影响

3 结论

(1)对穿锚杆针对沿空留巷中预留煤柱的支护能够起到有效的作用，通过室内相似试验以及数值模拟可以得出，当锚杆密度增加后，锚固体的峰值强度以及峰后强度均有所增加.但是对于煤岩而言，其峰后力学性能对安全生产更有价值.当锚杆密度从9增加到16，再增加至25 根时，其应力应变曲线可以明显看出，峰后强度明显的增加，而弹性模量却没有较大变化.也就是说，锚杆密度的增加并不能有效改善锚固体的弹性模量这一参数，即不能改变锚固体峰前的应力应变关系.

(2)锚固体中锚杆密度增大后，其等效内聚力继续增加，其增量ci与锚固体峰后强度增量si之间，符合正相关关系

ci=3.599si+1.458 2.

该公式对锚固体峰后强度的研究、巷道围岩的峰后力学特性以及煤岩巷道锚固支护方式的研究意义重大.

(3)锚杆直径的改变对锚固体的峰值强度以及峰后强度均有影响，当锚杆直径提升至一定值后，其峰后稳定强度并没有得到较大的提升.锚杆直径从4 mm增大至6 mm后，其峰后强度稳定到一定范围内，强度提升不大.实际工程中对锚杆直径的使用，只需能承受要求荷载即可.