基于JSD自适应粒子滤波的移动机器人定位算法

刘红林，凌有铸，陈孟元

(安徽工程大学 安徽省电气传动与控制重点实验室，安徽 芜湖 241000)

移动机器人定位就是确定机器人在其运动环境中的世界坐标系的坐标[1]，是机器人利用上一刻位姿和最新观测信息来估计当前位姿的过程。移动机器人定位可以通过多种方法实现。蒙特卡罗[2]定位作为粒子滤波在移动机器人领域的成功应用,最早由Dellaertt[3]等提出。粒子滤波对后验概率密度函数直接进行蒙特卡罗采样使其逼近真实的概率分布,因而被广泛应用在非线性系统。但是基于粒子滤波的MCL算法利用观测似然评估每个粒子的重要性权重,在采样环节中对先验分布进行采样,忽视了当前观测信息,在预测过程中可能会出现粒子分布在似然函数的尾部的情况,从而引起粒子退化问题。目前，针对粒子退化问题主要有增加粒子数目、改进提议分布以及改进重采样算法。第一种方法是扩大粒子数，但是比较低效，所以主要用选择合适提议分布和对重采样环节进行改进的方法来抑制粒子退化问题[4]。目前，提议分布的选取策略有将状态转移函数当作提议分布、把似然函数当作提议分布和混合提议分布等[5]。由于混合提议分布既考虑了状态转移函数，又考虑了似然函数，所以得到的重要性权值方差更小。虽然得到了较小的方差，但是在计算重要性权重时，难以实现计算过程中的积分运算。如果似然函数的分布呈峰态分布，那么采样效率低下[6]。粒子滤波是用样本来近似表示概率密度函数，用样本均值取代积分过程，得到最小方差估计。如果粒子数较小，算法的误差大，估计精度低，理论上如果粒子数目可以趋于无穷大，算法能够得到最优估计，估计精度最高。可是粒子数量的大幅增加使得系统的计算量剧增，算法在实时性方面不能达标，其不足之处在此体现。Rao-Blackwellised[7]滤波方法的提出则从另外一个方向提高了算法的实时性。此方法通过HMM滤波、KF、PF算法三者结合，分开估计状态向量中成员，使得估计维度减小，从而系统计算负担得以减轻。Kwok[8]等提出RTPF算法，将粒子集通过扩展估计窗口进行划分，使其成为一个个小粒子集，然后将小粒子集的估计结果通过赋予不同的权值重新组合获得估计结果。研究者们将粒子集分割成相同大小的集合，以KL距离(Kullback-Leibler distance)为指标来获取各集合的接近程度，从而动态调整粒子的数量提高实时性能。当算法性能较高时，采用较少的粒子数，否则采用较多的粒子数，这样既满足了滤波精度的要求，又减小了系统的计算负担。由于KL距离没有对称特性[9]，所以当概率密度先后次序改变时，所得到的值也会改变，那么对集合间接近程度的衡量结果就会不准，采样粒子数量的选择也会受到影响，最终影响到估计结果。

研究在一般粒子滤波算法基础上,通过对建议分布及重采样过程加以改进，提出基于改进粒子滤波的移动机器人定位算法。该算法将先验转移概率密度和观测似然概率密度的混合分布作为提议分布，将当前观测信息融入进去，在混合分布基础上，利用退火参数调控两者在混合提议分布中的比例，对于退火参数取定值时的不足，通过优化机制对参数进行在线变更。同时，利用JS距离获取子集间接近程度，确定采样粒子的总数，动态改变粒子的数量。实验结果显示，改进算法在一定程度上解决了粒子退化以及多样性缺失问题，减少了定位所需粒子数量，减轻了运算负担，提升了算法精度。

1 移动机器人蒙特卡罗定位

定义移动机器人系统含有噪声的运动学方程和观测方程为：

(1)

式中,xk表示k时刻的运动状态;f表示状态转移函数;uk表示k时刻的控制变量;ωk表示控制噪声;zk表示系统在k时刻的观测信息;g表示观测函数;vk表示观测过程中产生的噪声。

定位的最终目的就是要获得机器人在当前时刻的状态xk。从贝叶斯滤波角度，问题求解的核心是估计后验分布Bel(xk)。蒙特卡罗定位将具有不同权重的粒子重新整合，以此对k时刻机器人状态的后验概率进行估计。首先是重要性采样[10]环节，从重要性概率密度q(xk|xk-1,zk,uk-1)采集加权粒子集合。再经过重采样步骤，得到此刻状态后验Bel(xk)的离散估计。最后，为了解决积分难的问题，采用蒙特卡罗方法以采样粒子平均值作为状态估计结果。

(2)

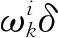
(3)

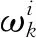
(4)

蒙特卡罗定位中建议分布的设计没有融入当前观测信息，把状态转移函数作为建议分布,即

q(xk|xk-1,zk,uk-1)=p(xk|xk-1,uk-1),

(5)

重采样算法被用来克服样本退化问题，在实际操作中，直接将评分过低的粒子舍弃，对评分高的粒子进行复制，重采样之后保持粒子群数量基本不变。蒙特卡罗定位算法中重要性密度函数的设计，忽略了最新观测zk对算法的影响，通过预测过程获得的粒子集合会分布于似然函数的尾部,出现粒子退化现象，进而影响定位结果。

2 改进的蒙特卡罗定位算法

2.1 改进的粒子提议分布

针对粒子滤波中出现的粒子退化现象，采用设计更为合理的提议分布的方法来抑制粒子退化。学者们对先验分布和后验分布进行研究，分析两种分布所具有的优点和缺点，在此基础上混合提议分布思想出现了[11]。混合提议分布将两种不同的分布放在一起进行研究。当前最新观测信息的引入，使得混合提议分布比两种单独的提议分布具有较小的权重方差。可是，重要性权重的运算过程中出现了积分环节，难以完成。另外，在似然函数分布呈现出峰值分布的时候，采样的效率极低[12]，所以使用退火参数来调整混合提议分布中各分布之间的比例。如果提议分布中的退火参数取值不变，因为概率分布具有不确定特性，所以滤波算法的性能较差。鉴于此，依据预测数据和观测数据的关系来自动调整退火参数定位数值，实现自适应优化的目标。

在选择建议分布q(xk|xk-1,zk,uk-1)时，将最新观测zk融入到建议分布里，让采样环节得到的粒子集中地分布于高似然区域，能有效减轻粒子集合退化问题,提升滤波器性能。将先验转移概率密度和观测似然概率密度的混合分布作为重要性密度函数，既考虑到运动模型又考虑到观测模型，因此建议分布为：

q=p(zk|xk)p(xk|xk-1,ut-1)Bel(xk-1),

(6)

其相应的重要性权值计算式为：

ωk=ωk-1p(xk|xk-1,zk-1),

(7)

当使用退火参数对不同分布的混合率进行调整时，建议分布选择为：

q=p(xk|xk-1,ut-1)cp(zk|xk)1-c,

(8)

则重要性权值计算式为：

(9)

其中，退火参数0≤C≤1。自适应调整退火参数的核心思想是在重要性采样之后，对预测值和观测值进行观察比较，当观测值比预测值大时，减小样本重要性权重的占比，将C的数值往下降。反之，将C的数值往上升。

2.2 基于JSD的重采样

重采样过程的引入会产生粒子多样性缺失问题，现采用遗传学中的变异操作[13]对粒子集进行优化。将粒子分为高权重、低权重两种，高权重粒子直接参与重采样，低权重粒子经过变异操作后再参与重采样。按式(10)确定低权重阈值，划分出高权重粒子和低权重粒子。

(10)

(11)

式中，Lmax是群体中最大的适应度值；Lavg是每一代群体中平均的适应度值;L是要进行变异的个体的适应度值;Pm1和Pm2对应的是变异概率的最大值和最小值;β是常数。

粒子滤波使用采样粒子与其权值的组合来表示系统后验估计，其结果总存在误差。理论上，粒子数目的大小对最终值的精确度会起到一定作用，当集合中粒子数目比较低的时候，最终值的误差会较大，反之当集合中粒子数目比较高的时候，同时在粒子数目逼近无穷大时，算法精度最高[14]。因此，当选择粒子数目的时候，必须更加全面地去思考，如果选择的粒子数目比较低，那么算法的精度就会降低。但是如果选取过多的粒子，算法在每次迭代过程中要对每个粒子进行运算，导致计算量大幅增加，不能满足算法的实时性处理需求。

FOX D利用KLD距离采样对其重采样部分进行改进，自适应地改变重采样过程中需要的粒子数目。KL距离具有不对称性，所以不同的概率密度顺序对应着不同的距离值，依此得出的相似度结果并不准确，那么粒子数目的确定就会不合理，对算法性能产生影响。JSD可以克服KLD不对称性的缺陷，使算法获得更好的精度。JSD可以计算分布S={s1,s2,s3,…,sn}与分布O={o1,o2,o3,…,on}的相似程度：

(12)

JS距离采样核心思想是将样本集合一分为二，利用JS距离计算两者的相似程度，并且设置两个门限Sl、Sh。如果JS距离小于低限Sl，那么两者具有高相似度，有一些非必须粒子存在，此时选取少量粒子进行系统状态估计，反之JS距离大于高限Sh，说明两者具有低相似程度，应适当增加粒子总数进行系统状态估计，粒子数按式(13)计算：

(13)

式中,n为粒子总数。

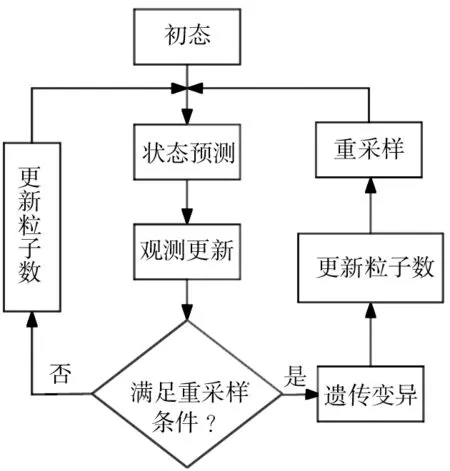
图1 改进粒子滤波流程图

图1是对标准粒子滤波算法进行改进后的算法流程图。在更新过程之后，判断是否满足重采样的条件，如果条件满足，则对更新后的粒子集进行变异操作，得到新的粒子集。然后将粒子集合随机划分为大小相等的两个子集，计算它们之间的相似度，根据式(13)调整粒子数，最后进入重采样过程。

2.3 改进后的蒙特卡罗定位算法

改进算法的具体流程如下：

步骤1 在k=0时，初始化系统。

步骤2 重要性采样以及权重计算。根据式(8)求取提议分布，并从中采样粒子。对每个粒子重新分配权重即权重更新。

步骤3 权重归一化。计算权重总和，进行归一化运算。

步骤4 重采样。判断是否满足重采样条件，如果条件满足，执行步骤5，反之，执行步骤6。

步骤5 根据式(10)划分高、低权重粒子，低权重粒子按照式(11)的变异概率进行变异操作。根据式(13)自适应改变粒子数目，对高权重粒子和变异产生的粒子进行重采样，得到新的粒子集合，同时更新权重。执行步骤7。

步骤6 根据式(13)自适应改变粒子数目。

步骤7 状态估计。把样本期望值当做此刻k的状态估计xk。

步骤8 令k=k+1,返回步骤2。

3 实验结果及分析

3.1 仿真实验

采用仿真实验来验证改进粒子滤波算法的有效性，并将其与利用KL距离采样的自适应PF算法作对比研究。使用Matlab 7.0软件进行仿真，机器人系统的状态模型和观测模型如式(14)所示[15]。

(14)

其中,系统噪声ωk～(0,10)，观测噪声vk～(0,1)。根据经验将算法中出现的参数作出如下设定：Sl=0.1，Sh=0.8，初始退火参数设置为0.3，即C=0.3，Pm1=0.1，Pm2=0.01，粒子总数设定为500。在上述参数条件下将采用KL距离采样的自适应PF算法与研究改进PF算法进行对比研究，每种算法分别进行100次试验，用误差均方根值(RMSE)以及有效粒子百分比(NEFF)作为指标对算法性能进行评价。

(15)

(16)

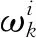
采用KL距离采样的自适应PF算法[16](图2～图8中记为KLPF)以及研究改进PF算法(图2～图8中记为AMJSPF)的误差均方根曲线如图2所示。由图2可知，在同等误差和状态下，改进PF算法的RMSE低于采用KL距离采样的自适应PF算法的RMSE。与采用KL距离采样的自适应PF算法相比，改进算法具有较好的估计精度。不同PF算法粒子数目的变化情况如图3所示。从图3中可以看出，两种算法都可以在线调整采样粒子数目，相比之下文中改进算法的采样粒子数目明显较小。粒子多样性对比图如图4所示。从图4可以看出,改进算法的粒子多样性较好。对两种粒子滤波器的性能进行比较，结果如表1所示。由表1可知，改进算法耗时较少，有较高的有效粒子数，粒子退化问题得以减弱。据此能够得出研究改进PF算法拥有较高估计精度，减弱了粒子退化问题，减轻了算法计算负担。

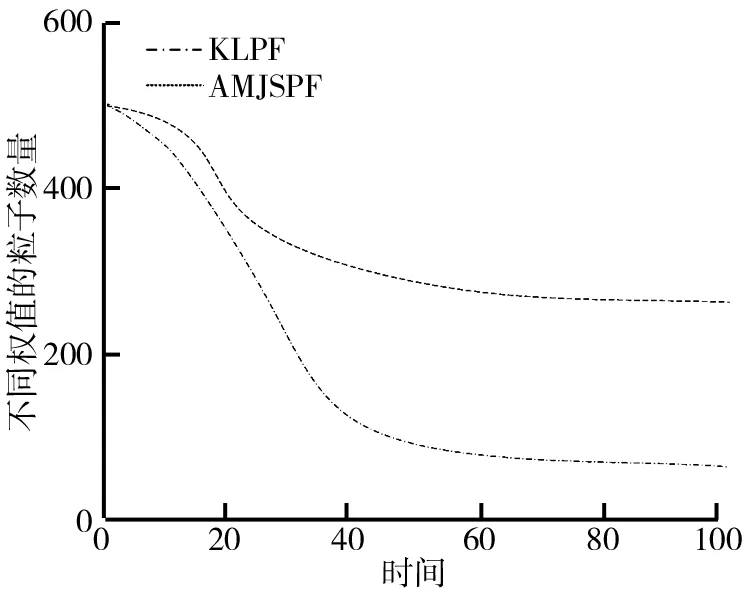
图4 粒子多样性对比图

表1 不同算法的性能对比

3.2 ROS上基于AMLSPF-MCL的机器人定位研究

在室内环境下利用机器人对基于KL距离自适应粒子滤波的蒙特卡罗定位和基于改进粒子滤波的蒙特卡罗定位算法进行对比试验验证。实验采用的平台为Turtblebot2机器人，其搭载了型号为Hokuyo UTM-30LX的激光传感器，在配有Windows7操作系统、i7处理器、4G内存的笔记本电脑上运行Liunx(Ubuntu 12.04)操作系统和ROS(hydro)。

利用Bailey发布的开源地图编辑器设计路标地图,地图区域为100 m×100 m,仿真中设定移动机器人从全局坐标(-10,-20)处开始运动,按规划点运动一周后返回起始点。过程噪声的方差设定为40，观测噪声的方差设定为2，移动机器人运行速度设定为0.35 m/s，粒子的数量设定为2 000，其他参数参照仿真实验进行设定。

采用KLPF-MCL算法进行定位的结果如图5所示。由图5可知，实线代表机器人的真实运动路径，虚线代表的是估计路径，由图5可知此次跟踪定位失败。AMJSPF-MCL定位结果如图6所示。由图6可知，机器人在采用AMJSPF-MCL算法进行定位时，虚线表示的估计轨迹与实线表示的机器人实际运动轨迹基本一致，跟踪定位成功。不同定位算法的粒子数目随着时间变动的改变情况如图7所示。由图7可以看出，AMJSPF-MCL算法所需粒子较少，稳定在80。不同算法的定位精度随时间变动的改变情况如图8所示。由图8可以看出，粒子的退化使得KLPF-MCL算法的估计精度降低，最终导致定位失败；AMJSPF-MCL算法由于有最新观测数据融入，使得估计精度平均值为19.051 cm，在一定程度上解决了粒子退化问题，可以得到较为精确的定位结果。两种算法的定位误差如表2所示。由表2可以看出，AMJSPF-MCL算法的精度比较好，耗时较少。

图5 KLPF-MCL定位结果 图6 AMJSPF-MCL定位结果

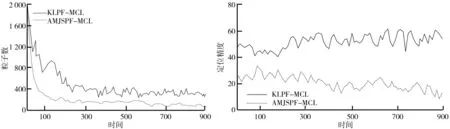
图7 粒子数随时间变化情况 图8 定位精度随时间变化情况

表2 两种算法的定位误差

4 结束语

研究所提的定位算法将先验概率分布和似然概率分布的混合分布作为提议分布，两者的混合比例用退火参数进行优化，利用自适应优化机制对退火参数进行动态优化，当前观测信息融入，对粒子退化现象起到了一定抑制作用。利用JS距离进行采样，动态调整粒子数量，减小了算法的计算量，增强了算法实时性，算法精度也得到提升。通过遗传变异操作，粒子多样性得到一定程度的保持。经过实验，改进算法被证明是有效的。研究中JS距离阈值所用的门限值没有进行严密的分析论证，并且在定位的过程中忽略了车轮打滑等影响算法精度的因素，后期将对算法继续进行完善。