非紧区域上算子值再生核的Mercer定理

陈文健

(烟台大学数学与信息科学学院, 山东 烟台 264005)

1 引言及预备知识

众所周知,再生核与再生核Hilbert空间理论已经被广泛的应用到机器学习领域,尤其在单任务学习领域的应用更为成功[1-5]．随着数据维数的不断提高,多任务学习已经渐渐的成为机器学习领域重要的研究课题．本文研究多任务学习中的算子值再生核以及向量值再生核Hilbert空间理论,其中被重构的函数来自一个Hilbert空间[6-8]．先简单回顾一下算子值Mercer核的概念,这是本文主要研究的对象．令(X,ρ)表示一个度量空间,其中度量为ρ．令H表示上的Hilbert空间,其内积为〈·,·〉H;B(H)表示由所有H上的连续线性算子构成的Banach空间．如果映射K:X×X→B(H)满足:

(i)K是对称的,即对于任意的x,y∈X都有K(x,y)=K(y,x);

(ii)K相对于由度量ρ诱导的拓扑在X×X上是连续的;

(iii)K是正定的,即对于任意的{x1,…,xn}⊂X和{v1,…,vn}⊂H都有

那么K称为B(H)值Mercer核．

根据Riesz表示定理知道对于任何一个B(H)值Mercer核K,存在唯一的Hilbert空间HK,其包含X上所有H值函数,内积和范数分别为〈·,·〉HK和‖·‖HK,且满足

K(·,x)v∈HK, ∀x∈X,v∈H

(1)

和

〈f(x),v〉H=〈f,K(·,x)v〉HK,

∀f∈HK,x∈X,v∈H.

(2)

称HK为向量值再生核Hilbert空间,K为其算子值再生核,且称等式(2)为HK的再生性质．

对于数量值再生核有著名的Mercer定理[9],而对于算子值再生核以及其对应的向量值再生核Hilbert空间的研究可以追溯到文献[10]．另外,文献[11-13]对各种底空间X也进行了深入地研究．特别地,在文献[13]中,Mercer定理被推广到具有有限测度的非紧区域上的算子值再生核上．本文的主要目标是建立具有σ有限的非紧区域上的算子值再生核上的Mercer定理．对于具有σ有限的非紧区域上的数量值再生核上的Mercer定理可参考文献[14]．

多任务学习近几年已经成为机器学习领域热门的研究领域,其中要学习的函数大多都是非紧区域上的向量值函数．本研究结果可以给多任务学习领域提供一些坚实的数学理论基础和新的研究方向．

为了给出主要结果,先回顾一下向量值函数的积分的概念．对于向量值函数的积分更多的理论可以参考文献[15-16]．假设X是一个局部紧的度量空间,以及(X,F,μ)为一个测度空间,其中μ是F上的Borel测度．先从向量值函数的Bochner积分开始,函数f:X→H称为是H值简单函数,如果

(3)

(4)

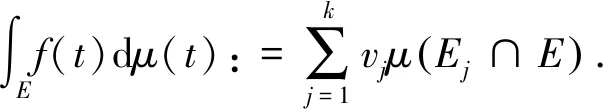
与数量值函数的Lebesgue空间类似,有下面的向量值函数情形的Lebesgue空间的定义．令L2(X,μ;H)表示包含所有X上H值Bochner可积的函数f的集合,且满足

2 非紧区域上算子值再生核的Mercer定理

对于B(H)值Mercer核K,定义算子LK如下:

算子LK称为由算子值核K定义的积分算子．假设:

A1: 对于任意的x∈X和v∈H,K(x,·)v∈L2(X,μ;H);

A2:LK是L2(X,μ;H)上的有界正定算子;

A3:LK有可数个正特征值{λj},其对应的标准正交特征向量为{φj}．

在上面的假设下,有命题1.

命题1 如果函数f:X→H是连续的且支撑在某个Xn0上,那么LKf∈HK．另外,对于任意的h∈HK都有

(5)

证明对于任意的x∈X,有

对于任意的x∈X,由K(x,·)和f都是连续的可得K(x,·)f也在X上连续．因此对于任意的Φ∈H*有Φ(K(x,·)f)是可测的,从而K(x,·)f是弱可测的．另外,由H是可分的和Pettis定理得K(x,·)f是可测的．所以由Xn0的紧性有K(x,·)f在Xn0上是Bochner可积的．

对于任意x∈X,因为K(x,·)f在Xn0上连续以及Xn0是紧的,所以K(x,·)f在Xn0上一致连续．所以对于任意>0,存在δ>0使得只要ρ(s,t)<δ就有‖K(x,s)f(s)-K(x,t)f(t)‖H

-K(x,t)f(t)‖Hdμ(t)<,

这就推出对于任意的x∈X有

(6)

这里,tn,j是在En,j中任意选取的点．

〈gn,gn〉HK-2〈gn,gm〉HK+〈gm,gm〉HK.

利用式(2)得

〈gn,gm〉HK=

其当m,n→∞时收敛到

类似地,有

所以,推出序列{gn}是HK中的Cauchy列．从而结合式(6)得到LKf∈HK．

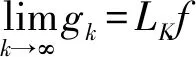
〈LKf,h〉HK=

其等于

即要证的结论成立．

引理1 设Cc(X;H)表示由所有具有紧支集的连续函数f:X→H构成的线性空间,那么Cc(X;H)在L2(X,μ;H)中是稠密的．

证明设f为L2(X,dμ;H)中任意一个元素,只需证明对于任意>0,存在一个g∈Cc(X;H)使得

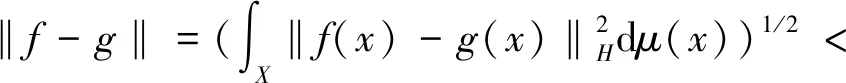
其中第二个等式由单调收敛定理得到．因此,存在一个正整数N使得

成立,而这可以推出

(7)

另一方面,显然有fj∈L2(X,dμ),j∈．由Cc(X)在L2(X,dμ)中是稠密的,故存在gj∈Cc(X)使得

(8)

上式结合式(7)就完成了我们的证明．

命题2 对于任意的g∈L2(X,μ;H),有LKg∈HK,且

(9)

另外,对于任意的h∈HK∩L2(X,μ;H)有

〈LKg,h〉HK=〈g,h〉L2(X,μ;H).

(10)

证明由g∈L2(X,μ;H),可以选取Cc(X;H)中的序列{gn}使得{gn}在L2(X,μ;H)中收敛到g．由命题1有LKgn∈HK．另外,有

gm(s)-gn(s)〉Hdμ(s)=

这意味着{LKgn}是HK中的Cauchy列,从而在HK中有极限f．注意到再生性质(1)和(2)得

〈LKgn-f,K(·,x)(LKgn(x)-f(x))〉HK≤

即

‖(LKgn)(x)-f(x)‖H≤

(11)

由Xm的紧性、K的连续性以及式(11)得{LKgn}在每个Xm上都一致收敛到f．

为了证明式(9)和(10),我们由式(5)计算得

以及

即要证明的结论成立．

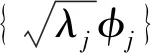
有了上面的准备工作,现在证明主要定理,即非紧区域上算子值再生核的Mercer定理．

定理1 设A1,A2和A3成立,那么对于任意的x,y∈X和u,v∈H有

〈K(x,y)v,u〉H=

(12)

另外,固定u,v∈H,则上面的级数在Y1×Y2上一致和绝对收敛,这里,Y1和Y2都是X中的紧子集．

(13)

因为{φj}是LK的标准正交特征向量,其对应的特征值为{λj},有λj=〈λjφj,φj〉L2(X,μ;H)=〈LKφj,φj〉L2(X,μ;H)≤‖LK‖.结合式(13)得到

令

由上面的讨论立即得到F(·,y,v)∈HK∩L2(X,μ;H)．因此,对于任意的j有

0=〈F(·,y,v),φj〉HK=

由{φj}的完备性得F(x,y,v)=0对于变量x在X上几乎处处成立．注意到μ是非退化的以及F(·,y,v)是连续的,有F(x,y,v)=0对于任意的x,y∈X和v∈H成立,即

再由内积的连续性就得到式(12)．

特别地,对于任意的x∈X和v∈H有

(14)

由K和φj的连续性,以及Dini定理[17]得式(14)右端的级数在任意紧子集Y1上一致收敛．另外,由Cauchy-Schwartz不等式得

由此得级数(13)在Y1×Y2上一致和绝对收敛,其中Y1和Y2为任意的紧子集．定理1得证．