中线定理及重心性质的统一形式

滕 旭

(云南大学 旅游文化学院,云南 丽江 674100)

1 三角形的中线定理及重心性质

1.1 证明

为了研究中线定理的统一形式，本文采用统一的符号表示.

如图1所示，设ΔA1A2A3边AiAj中点记为Mij(1i,j3且i≠j)，三条中线交于一点称为三角形的重心记为G，则有如下关系：

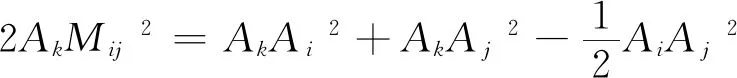
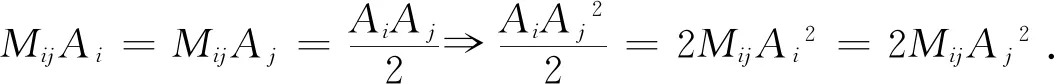
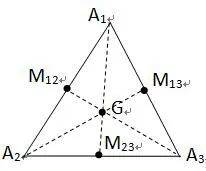
图1 三角形的中线定理与重心

证明：用向量法证明中线定理及重心性质[1].

证明重心性质如下：

设三角形的三个顶点坐标为A1(x1,y1)，A2(x2,y2)，A3(x3,y3)

同理：G∈A2M13，G∈A3M12，因此三角形三条中线交于一点G且G分每条中线为2∶1的两部分.

证明中线定理如下：

(1)

(2)

得到中线性质定理初始形式，再根据定理注解，问题得证.

1.2 应用

等边三角形的中线即为高，利用中线定理可求边长为a等边三角形的高H如下：

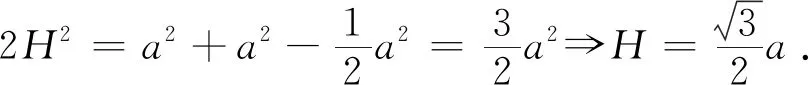
等边三角形的四心重合，根据三角形的重心性质可求边长为a等边三角形外接圆半径R及内切圆半径r如下：

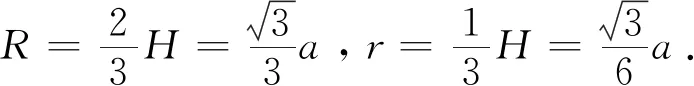
2 四面体的中线定理及重心性质

2.1 证明

如图2所示，四面体A1A2A3A4的顶点A1所对的面A2A3A4内的重心记作G1，其他四个面的重心分别记作G2，G3，G4，则称A1G1,A2G2,A3G3,A4G4分别为四面体的四条中线. 四面体的四条中线交于一点称四面体的重心记为G，则有如下关系：

图2 四面体中线定理及重心性质证明示意图

证明：用向量法证明中线定理及重心性质[2-3].

证明重心性质如下：

设四面体的四个顶点坐标为A1(x1,y1,z1)，A2(x2,y2,z2)，A3(x3,y3,z3)，A4(x4,y4,z4)

令

则证明重心性质如下：

同理：G∈A2G2，G∈A3G3，G∈A4G4因此四面体四条中线交于一点G且G分每条中线为3∶1的两部分.

证明中线定理如下：

如图1所示，

(3)

(4)

(5)

⟹3AlGl2=AlAi2+AlAj2+AlAk2-(GlAi2+GlAj2+GlAk2)

得到中线定理的初始形式.

再由三角形的中线定理及重心性质，

GlAi2+GlAj2+GlAk2=

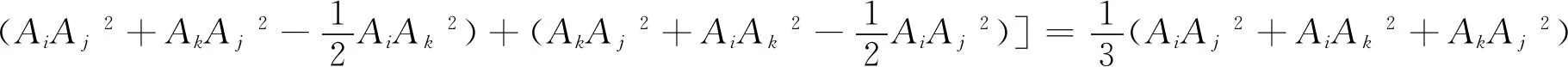
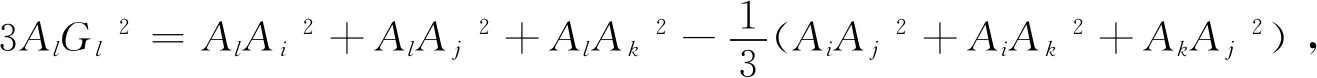
2.2 应用

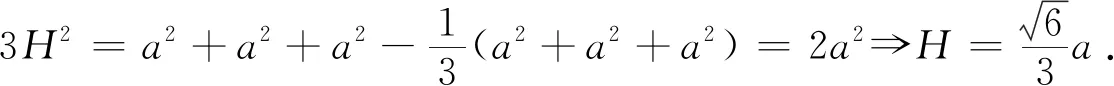
正四面体的重心，外心，内心重合，根据四面体的重心性质可求棱长为a正四面体的外接球R及内切球半径r如下：

3 中线定理及重心的统一形式

取n维空间上的n+1个点Ai(1in+1)构成n+1面体[6-7].

证明重心性质如下：

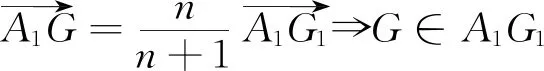
同理：G∈A2G2，G∈A3G3，…，G∈An+1Gn+1因此n+1四面体n+1条中线交于一点G且G分每条中线为n∶1的两部分.

显然，三角形及四面体的重心性质都可统一于上述形式，n=2时就为三角形的重心性质，n=3时就为四面体的重心性质.

证明中线定理如下：

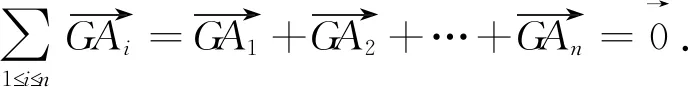
显然，三角形及四面体的中线定理初始形式都可统一于上述形式，n=2时就为三角形的中线定理的初始形式，n=3时就为四面体的中线定理初始形式.

三角形及四面体的中线定理都可统一于n+1面体的中线定理

n=2时就为三角形的中线定理，n=3时就为四面体的中线定理.

下面证明若n维空间上的n+1面体的中线定理成立，则对n+1维空间上的n+2面体亦成立，从而可对任意的n∈N+均成立. 记：

M={m|1mn+2,m∈Z}，M-i-j={m|1mn+2且m≠i且m≠j,m∈Z}

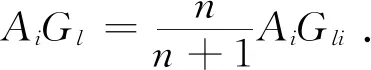
4 总结

中线定理及重心性质为三角形的基本性质，向量作为几何研究的手段具有很大的优越性，本文利用向量的方法将三角形的中线定理及重心性质推广到四面体，并指出三角形及四面体具有的此种性质实际上还可进一步推广至n维空间上的n+1面体中，从而给出一种统一形式，体现了数学的统一美.