侧装式垃圾车连杆提升机构尺度综合与分析

李 亮,卢军广

(1.东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066000; 2.新兴河北工程技术有限公司 铸管装备研究所,河北 邯郸 056107)

随着公众环保意识的提高,垃圾清运工具的开发成为社会关注的研究内容之一.侧装式垃圾车也称自装卸垃圾车、挂桶式垃圾车,因其具有集装速度快、二次污染小、路面占用空间小、装载效率高、可靠性高等优点,在采用标准化垃圾桶的社区环卫工作中得到了广泛应用[1].侧装式垃圾车目前普遍采用链条式和连杆式两种提升机构,其中连杆式提升机构设计简图如图1所示,垃圾桶通过结构件刚性联结于滑块BCD上,C1D0为两套导轨分别约束C点和D点,提升阶段两套导轨共同约束,主动臂OA通过连杆AB带动滑块沿导轨向上运动至D0点;翻转阶段C点约束失效,当主动杆继续转动时,滑块以D0为固定铰点向上翻转,将垃圾桶中的垃圾倾倒至车厢.复位阶段在垃圾桶自重及液压缸的推力作用下，主动杆反向转动将垃圾桶复位至原位.因此，该机构为滑块和四杆组合机构,完成作业自由度数不变只需一个液压缸动力源,且主动杆为异形结构件可作箱盖之用.简洁起见,图1中未体现垃圾桶挂取装置、液压缸及其铰点.文献[2-3]结合该机构的工程应用,对结构组成、工作原理、工程方案做出了详细阐述和初步的理论探讨.文献[4]对垃圾桶夹持装置的力矩进行了分析.目前,针对该机构的尺寸综合与分析仍缺少科学详尽的理论指导.

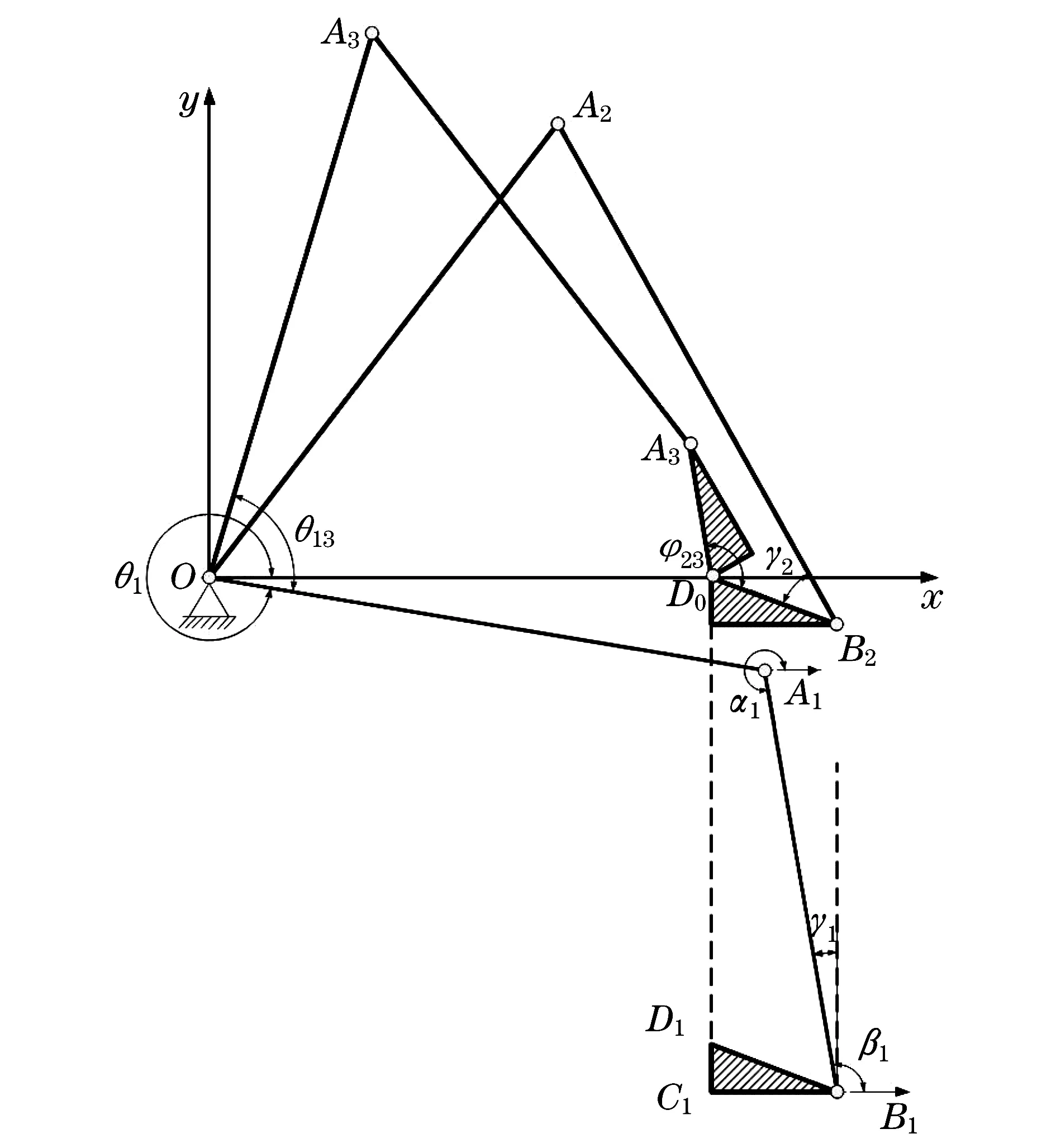
图1 连杆式提升机构的设计简图Fig.1 Design diagram of the linkage mechanism for hoisting

尺度综合即按已知构型和运动学参数确定机构中各构件的几何尺寸,有图解法和解析法,传统的作图法精度低且过程繁琐,而解析法可实现点位精确综合和轨迹近似综合[5].文献[6]结合新式飞机机翼支撑平台的开发，探讨了优化综合方案，得到了机构最优尺度参数.文献[7]针对四位置刚体引导机构综合,采用位移矩阵法给出了布氏曲线方程,直观地描绘了机构解域.文献[8]通过三位置坐标和姿态，将刚体导引机构的尺度综合引入到水稻钵苗移栽机构的设计中.文献[9]详细介绍了位移矩阵法进行机构尺度综合应用于门座起重机的具体案例,对垃圾车提升机构进行尺寸综合与分析具有重要的工程意义.

1 基于位移矩阵法的提升机构尺度综合方法

由工作原理可知,该机构的综合需满足垃圾桶提升高度、翻转角度、车厢开口长度及箱盖上掀角度等运动学因素,为保障机构传动性能良好,还应综合考虑最小传动角的约束,确定各杆长度及转角.因此，属于刚体引导机构综合的问题,采用位移矩阵法进行求解.以主动杆固定铰点为坐标原点建立坐标系(见图1),设主动杆杆长为l1,由运动关系A1点坐标可表示为

(1)

点A从位置1绕O点逆时针旋转至位置3,若给定其旋转角度为θ13,由刚体位移矩阵可求得A3点坐标为

(2)

若给定车厢水平开口长度OD为l3，提升点起至车厢上沿高度C1D0为h,BC两点间结构允许的最小安装距lBC,则B1,B2,D0点坐标为B1(l3+lBC,-h),B2(l3+lBC,-lCD),D0(l3,0).刚体BCD从位置2至位置3需旋转φ23,位移矩阵为

(3)

D0点为刚体BCD的平面运动的转动极,则B3点坐标可求[10]，即

(4)

在位置1和位置3时连杆AB杆长不变,有约束方程

(5)

式中未知量有l1,θ1和lCD,而方程只有1个.为保障机构重载时具有良好的传动性能,给定图1所示约束压力角γ1和传动角γ2,由A1,B1两点坐标可得

(6)

引入未知量OA杆翻转临界状态时转角θ2,则A2(l1cosθ2,l1sinθ2)有定杆长约束

(7)

根据传动角γ2的几何关系有

(8)

根据式(5)～式(8)得4个方程,4个未知量l1,θ1,lCD和θ2可全部得解.

选定设计参数,方程化简后经Matlab求解算例,如表1所示.进而求得AB杆长l2为1 012.061 mm,翻转杆BD杆长l4为220.527 mm.

表1 算例设计参数及结果Tab.1 The specified parameters and results of case

2 运动分析

运动分析是动力学设计分析及优化的基础,同时也是机构综合结果的检验手段[11].鉴于该机构主要作业过程分为两构型阶段且自由度不变,因此，首先建立滑块机构的封闭矢量方程为

以复数形式表示为

设B点坐标(xB,yB),则有位移方程

θ1<θi<θ2

(9)

翻转阶段为四杆机构,有封闭矢量方程，即

以复数形式表示为

则位移方程为(此时θ2<θi<θ3)

(10)

求解方程组得

其中,

综上代入算例数据,经Matlab编程计算结果如图2所示.

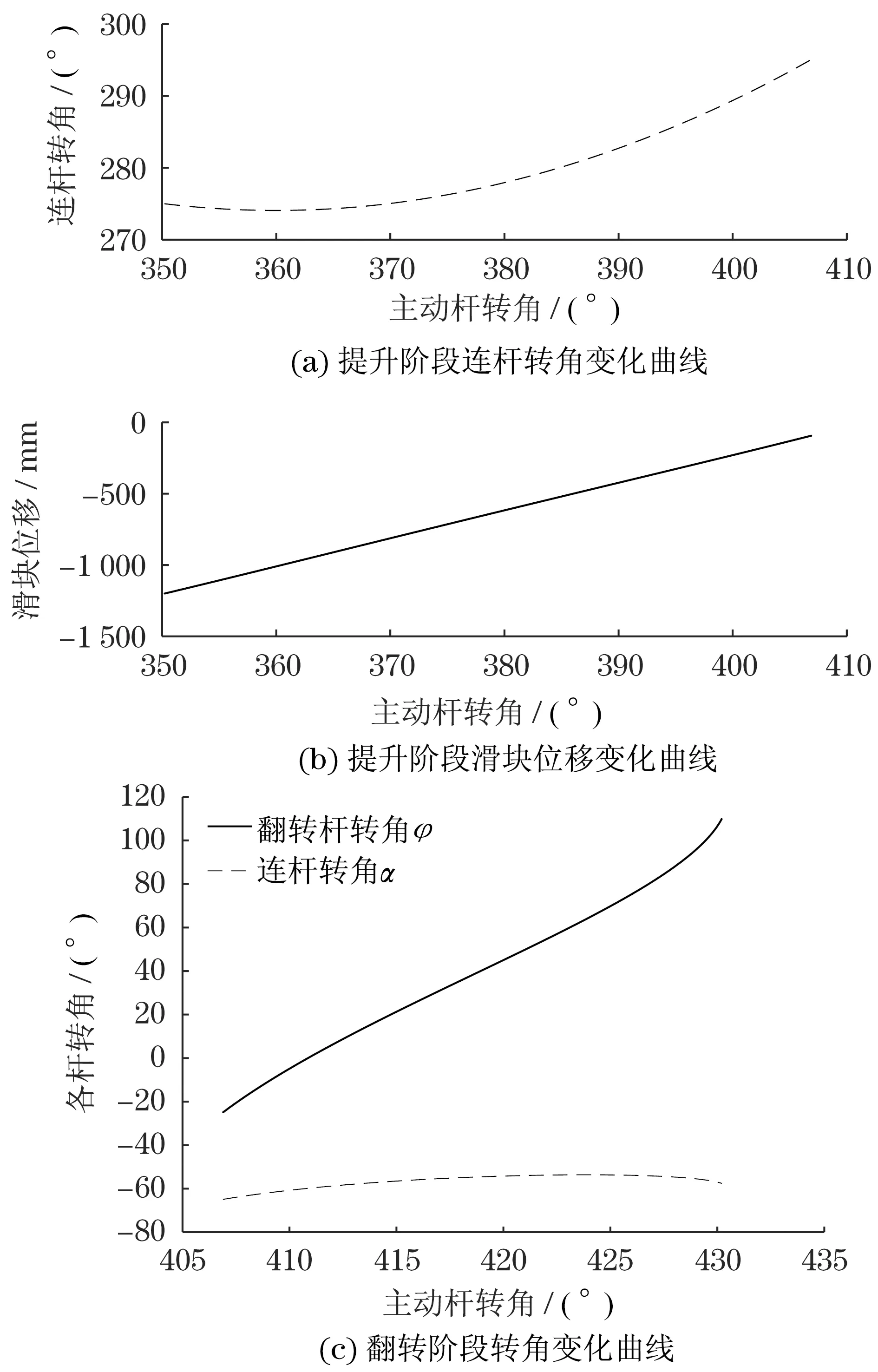
图2 提升机构算例运动规律Fig.2 Kinematic rules of hoisting mechanism for the case

图2表明整个作业过程主动杆从350.21°转动至430.21°上掀80°.图2(b)中滑块竖直提升1 107.091 mm后,由图2(c)可看出翻转杆从-24.95°转至110.05°转动135°，符合预定设计目标.各位移量曲线平滑无数据突变,表明整个机构运动过程无奇异点.经计算压力角γ1从5°变化至11.97°,符合一般传动机构最小传动角要求[10](>40°),因此，传动性能良好;传动角γ2最大为90°,最小出现在翻转终止位置为12.42°,因该位置垃圾桶近空载且可依靠其自重回程,所以基本符合运动要求.

3 液压缸铰点位置综合

液压缸作为机构动力源,要求活动铰点应与主动杆(箱盖)转动角度相同.限于实际安装布局,液压缸固定铰点宜位于车厢边缘且在箱盖上方,同时应保证传动性能良好[12].图3为液压缸铰点布置示意图,其中，T1,T2为箱盖转动角度为θ13时液压缸两极限位置.

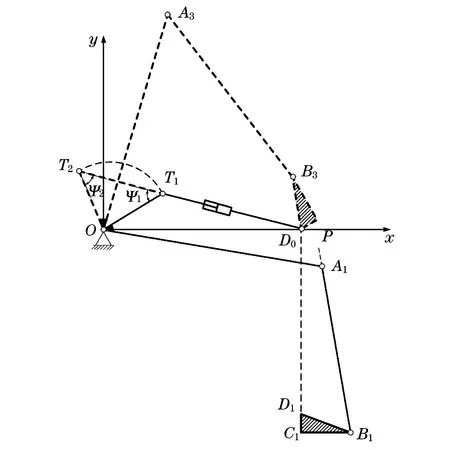
图3 传动角最佳时液压缸的铰点位置Fig.3 The hinge position of the hydraulic cylinder when the transmission angle is optimal

令l3=1,摆杆OT长为s,ε=s/l3,液压缸伸长系数λ=p2/p1,则传动角ψi有如下关系式[13]:

(13)

由式(13)可知,机构有最大为90°的传动角时需ε<1.工程中,ε常用区间为(0.25～1.00)[14],令ε取不同值时,压力角随液压缸长度p变化曲线如图4所示.

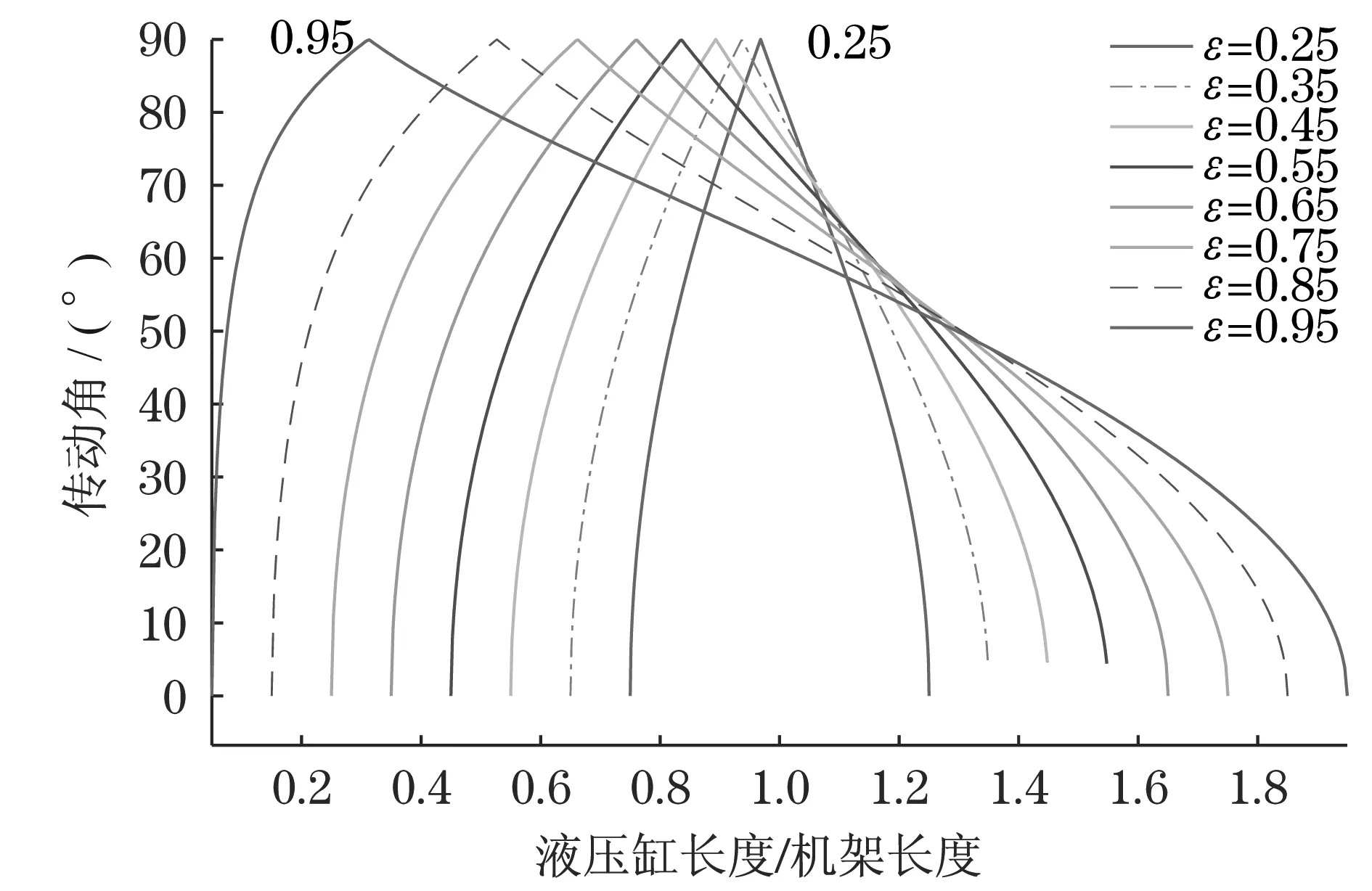
图4 传动角与液压缸长度关系曲线Fig.4 Curve of the relation between curve transmission angle and length of hydraulic cylinder

由图4可知:在归一化的各杆参数中，随着ε的增大,摆杆转动180°所需液压缸伸长量越大,即要求摆杆做大幅摆动时ε宜取较小值;随着液压缸的伸长摆杆转动180°,压力角先增大至极值后减小,为保证液压缸在规定摆角内机构获得最优传动性能,宜取液压缸两极限位置具有相等的传动角,即ψ2=ψ1.

由上述分析可知,当给定摆杆转动角度θ13及机架长l3时,若指定液压缸的伸长比λ或液压缸初始长度p1,则由式(13)可求得传动角最优的液压缸布置参数算例,如表2所示.

4 力学分析

刚体引导机构的综合是以位移要求作为依据,因此，需将力学特性计入分析才能应用于工程实际[15].以箱盖TOA为研究对象,对O点取矩,则∑MO=0,有

表2 最优传动角的液压缸铰点参数算例Tab.2 The case of hinge point parameter of hydraulic cylinder with optimum transmission angle

(14)

式中:F1为提升阶段液压缸推力;FAB为箱盖所受拉杆的力;lO为FAB的力臂.

因

(15)

式中:G为垃圾桶所受重力.

由于箱盖上两杆OE,OA为刚体联结,有

(16)

综合式(9),αi与θi的关系可得FAB由p表达的关系式.由A,B两点坐标可得其力臂长度为

(17)

由式(13)及归一化的参数关系可得

(18)

综上,由液压缸推力F1即可建立与液压缸长度pi的映射关系.同样翻转阶段的关系式为

(19)

对D0点取矩,则有

(20)

式中:lBD为G的力臂(注:此时力臂大小需根据垃圾桶重心位置确定);lD为FAB的力臂.

由A,B两点坐标(l1cosθi,l1sinθi),(l1cosθi+l2cosαi,l1sinθi+l2sinαi),易求得直线AB方程.由点到直线距离公式得

(21)

式中,

至此，结合式(10)～式(12),代入算例已知数据,即可求得液压缸两个推力F1,F2.以负载为标准240 L垃圾桶为例[16],取重心距B点水平距离300 mm处,其重力1 000 N.经Matlab编程求解结果如图5所示.由图5可知:液压缸最大推力出现在提升初始阶段,最大推力4 145 N;在翻转临界状态由于运动形式变化出现力的突变,差值为368 N.图5(b)表明:随着垃圾桶重力力臂的减小而后推力减小至接近0 N,此时垃圾桶翻转101.3°;翻转末段由于连杆传动角的变小以及未计入垃圾桶卸载状态参数,推力急剧增大至近3 000 N.整体计算结果反映出油缸受力状态符合运动规律,算例机构尺度参数基本满足实用要求.

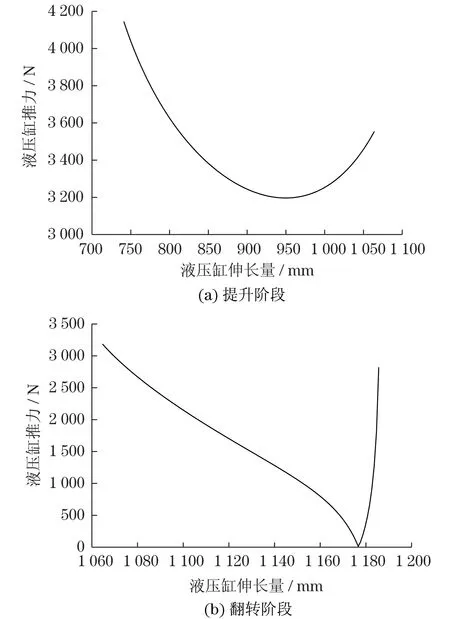
图5 液压缸推力随行程变化曲线Fig.5 The curve of the thrust of hydraulic cylinder changing with the stroke

5 结论

(1) 侧装式垃圾车连杆提升机构具有两个作业阶段的刚体导引要求,采用位移矩阵法对其进行尺度综合,方案实用性强，可有效避免传统作图法冗杂繁琐的试凑过程.

(2) 通过对该机构运动及力学特性分析,结果表明算例机构基本能够满足工程需要.鉴于所需液压缸最大推力出现在提升初始阶段,后续设计应调整液压缸铰点位置将该处传动角最大化.同时工程应用中，在结构尺寸条件允许下，将垃圾桶重心位置尽量靠近铰点B处,且为尽量减少运动冲击,在翻转铰点D0处应增加弹簧阻尼元件.此外,为减少翻转初段垃圾遗洒,宜向车厢内布置一段弧形导轨.

(3) 整体综合及分析的数学模型为后续该型提升机构的优化综合提供了参数化支撑,进一步的机构学研究可结合平稳性、液压缸峰值推力进行多目标优化.但由于该机构作业过程分两个阶段,一些角度变量的定义域呈分段函数,目标函数的加权处理应予以重视.

(4) 整体分析表明侧装式垃圾车连杆提升机构具有空间布置灵活、性能优良等特点,在中小型垃圾清运车领域具有广阔的市场空间.