从高考题到阿基米德体

文／沙国祥

图／张志勇

（2019年全国Ⅱ卷第16题）中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有____个面，其棱长为____.

图1

图2

本题第二空难度较大.题中出现了一种特殊多面体——“半正多面体”，对于它的结构描述“它的所有顶点都在同一个正方体的表面上”，很多同学觉得难以理解和想象，因而无法顺利作答.

事实上，这种“半正多面体”就是所谓的“阿基米德体”.这类多面体是由正多面体切割而得，各面上出现的多边形是两种或两种以上的正多边形，每个顶点处都由相同种类和顺序的正多边形围成.如图2，此阿基米德体的每个顶点都是由一个正三角形、三个正方形围成，自然，它们的边长都相等啦！这个阿基米德体是由一个正方体（我们称之为“原初正方体”）切割而得.

但因为原初正方体未出现，因而不易想象切割后的阿基米德体与原正方体的关系.

同学们可以发挥想象力求解：

如图3，考虑到对称性，八边形ABCDEFGH是正八边形，其八个顶点位于同一平面上.想象一下，此正八边形的上面两个顶点A，H位于原初正方体的上表面，下面两个顶点D，E 位于原初正方体的下表面.画出平面直观图，如图4：

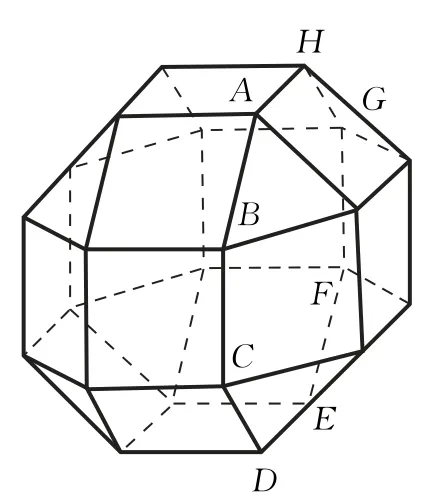
图3

图4

分别延长上下、左右的相对两条边，得到一个正方形，这个正方形其实是原初正方体的一个平行于一个表面的截面，其边长正是正方体的棱长1.

设正八面体的边长为x，根据图4，从正方形的边长为1可得方程

此即“半正多面体”的棱长.

只是做完这道高考题，还不能压住我们心头的好奇和疑问：那个“原初正方体”在哪儿？怎样由这个原初正方体切割成高考题中的阿基米德体？阿基米德体我们以前见过吗？一共有多少种？下次还会考吗？

我们知道，一个正方体由六个面组成，分成三组，每组中两个面互相平行.大家仔细观察一下图2，这个阿基米德体的上下、左右、前后三组，共六个小正方形（或者水平，或者竖直），正位于原初正方体的相应六个面上，它们并没有被切割掉啊！展开你想象的翅膀，依据这六个小正方形就可以作出所在六个平面，复原“原初正方体”（如图5，查看动画请扫描文末的二维码）.这样就更容易理解上述解法了.你甚至可以通过延长小正方形的边作出原初正方体的棱.再看图6，这是另一种观察视角.

图5

图6

阿基米德体非常罕见吗？高考命题者就是要找些稀奇古怪的玩意儿“捉弄考生”？其实，阿基米德体我们人人都见过，最常见的足球“电视之星”（如图7），就是由一个阿基米德体充气后膨胀而成的.这个阿基米德体，是在一个“原初正二十面体”的12个顶点处切割掉12个小五棱锥得到的（如图8）.因此，一个常见的足球上，就有12个五边形，20个六边形.

图7

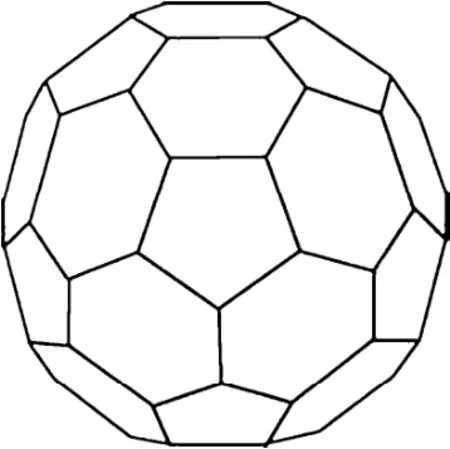
图8

高考题中的阿基米德体你可能没见过，但它的兄弟就活跃在足球场上，你留心过吗？研究过它的数学结构吗？如果由此及彼，再追问：这种足球是哪类立体图形？同类图形还有哪些？那你不就接近甚至发现高考题了吗？

最后告诉你，阿基米德体一共有13种（具体可参考《数学文化素质教育资源库》中的《数学之美》分册）.它会不会以后再考？很难说，可能会以另一种形式考也未可知.所以，学习不必太顾眼前，风物长宜放眼量，你关注数学文化，了解数学问题、方法的历史背景、来龙去脉，说不定哪天就碰上高考题了.