从零的零次方无意义谈起
——代“概念理解专栏”发刊词
江苏省吴江盛泽中学 孙四周
概念有四个要素,第一要素就是“意义”(另外的三个是:事例、特征、符号).作为这个专栏的首篇,为什么不谈“意义”而是谈“无意义”呢?请往下看.
数学上印象最深的“无意义”,可能是小学时的“0做除数”,当时的说法是“0不能做除数”,后来又说成“0做分母无意义”.初中有了“负数开平方无意义”,高中又有了“00无意义”,等等.数学上许多东西都是人为规定的,为何还有那么多的无意义呢?为什么不给它们“规定”一个意义?
现在来看00,如果允许你去规定,你认为该规定它等于多少才算合适呢?如果注意到这个序列:
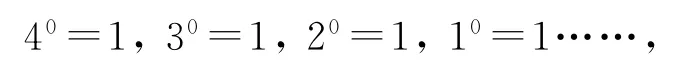
应该规定00=1;
而对于这个序列:

似乎又该规定00=0.
数学家们还发现了类似的其他序列,按照那些序列呈现出的“规律”性,00又似乎是另外的值!进一步的研究可以发现,对于任何一个正数,我们都可以找到这样的序列,使得序列的“规律”指向它.如此一来,你认为该规定00等于哪个值呢?
所有的“规定”都是人为的,但人不可妄为.数学上,在有了必要性和可行性时,才会去进行人为的规定.即数学上的某个东西非常重要,“必须”有意义,否则就会有很多困扰;而它本身又没有“现成的”意义,这时数学家就会尝试去规定一个.这个“规定”自然要满足两点:一是要解决存在的困扰,二是不能引发新的矛盾.比如,“任何数乘以0都等于0”就是一个人为规定,它解决了乘法运算的很多问题又不引起矛盾.如果你规定“任何数乘以0都等于这个数”,那就会引起矛盾,因而不能采纳.
00 的意义,需要规定吗?好像是的,在心理上我们总希望自己看到的东西是有意义的.那么,可以规定00的意义吗?现在还没有找到规定它的方法,也就是:规定它等于任何一个实数都会导致矛盾.如此,只好不做规定.也就是认为00无意义.你是不是感到很遗憾?没必要,“00无意义”就是它的意义.

人类总是在寻找世界(和人生)的意义,也总希望自己感受到的东西、经历过的事件是实在的.如果你突然发现,面前站着的人是“虚幻”的,那个感觉可不美妙.在逻辑上证明某个东西“不可能有意义”,比认定一个东西“有意义”要困难得多.因此,对数学上“无意义”的东西我们会有深刻的记忆,深刻程度超过众多“有意义”的东西.
我们今天在这里谈“无意义”,希望大家注意以下两点:
第一,“无意义”和“有意义”是相对的,无意义可以发展为有意义,有意义也可能变得无意义.比如:7除以3无意义(除不尽)、小数减大数无意义(不够减)、大于180°的角无意义(不存在)等,现在它们都变成了有意义.还有很多的无意义,比如:负面积、负数开平方、负数的对数等,在以后也会变得有意义.每一次把无意义转化为有意义,都是认识上的巨大突破.
第二,某些看似天然“有意义”的概念被质疑,即被怀疑为“无意义”,会促进人们的思考,突破眼界的局限,进入新的认知领域.
比如“线段长度”,意义似乎非常清楚,只要是认识数码的人就会利用刻度尺把一个长度量出来,似乎没什么好研究的.而实际上,“尺子量出来”的那个数据是很表象化的东西,知道它“能不能度量”才是深刻的.由此前沿的思想家们考察了曲线的长度、不连续数集的长度、海岸线长度等,发展出了微积分学、勒贝格测度、分形理论等彪炳史册的伟大理论.即便现在,对于空间、时间等基本概念,人类还没有认识清楚,这已经是科学的最前沿了.
概念,是逻辑思维的结果,也是思维过程的凝结,还是继续思维的载体.人类的灵性,就体现在对抽象概念的理解和应用上.这,也是我们开设“概念理解”专栏的意义.我们会把更多的意义揭示出来,以飨读者,也让我们的学习充满意义.


