旋转液膜反应器高度对临界流量影响的研究

谢震非 许兰喜 李殿卿

(北京化工大学 理学院， 北京 100029)

引 言

沉淀法是制备纳米材料主要手段之一。传统搅拌釜反应器由于自身结构以及反应物混合效率的局限，无法对沉淀反应过程精准控制，影响了生成物作为功能材料的性能。Guo等[1]使用旋转液膜反应器研究可控的沉淀反应后发现，该反应器的沉淀产物与传统反应器相比粒径更小，而且沉淀产物的粒径分布范围更窄，同时当给定间隙和转速时，反应物溶液进入反应器的流量为一固定值，此时不会有空气随物料进入反应器；当流体的加入速度小于固定流量时，旋转液膜反应器的反应空间中会被带入大量空气，导致沉淀反应的影响因素复杂化，使反应器数学模型的建立十分困难，而当流体的加入速度大于固定流量时，物料将从反应器的入口处溢出。因此定义反应器在固定的间隙与转子转速下无空气进入且无物料溢出时的最大流量为临界流量(CVFR)。

临界流量是反应器进行纳米颗粒生成实验和产物粒径数值模拟的重要前提，文献[2-6]研究了旋转液膜反应器模型的流场，但没有涉及临界流量。艾俐博等[7]首次计算了不同间隙宽度和转速下的临界流量，但是得到的数值解相对实验结果的误差较大。董利君等[8]采用文献的计算方法研究了反应器侧面与底面夹角对临界流量的影响。

本文在文献[7]计算方法的基础上，考虑了壁面湍流对临界流量的影响并引入了边界层网格；采用可攀爬壁面函数替代增强型壁面函数，提高了壁面处的计算精度；采用网格自适应以及自适应时间步长以提高计算精度；同时采用Realizablek-ε湍流模型替换RNGk-ε湍流模型。计算发现，新方法得到的数值解与实验值吻合较好。在验证方法可靠性的基础上，分析了反应器模型临界流量随反应器高度的变化情况，并比较了临界流量对转子转速和反应器高度的敏感程度。

1 反应器数学模型

1.1 反应器几何结构

旋转液膜反应器由内部的转子、外部的定子以及导流区3部分组成，流体从导流区进入定子与转子的间隙。目前，实验室订制了新的旋转液膜反应器，新反应器高H=45 mm，上底半径R3=20.94 mm，下底半径R1=25.75 mm，侧面与底面夹角α=85°(原反应器H=17 mm，R3=20.4 mm，R1=25 mm，α=75°)。反应器转子绕z轴旋转，夹缝间隙d=R2-R1，值在0.1～0.5 mm之间变化；转子转速Ω在500～5 000 r/min范围内变化；导流区高度h取2 mm。实验中通过调节定子的半径R2来改变夹缝宽度。反应器具体结构如图1所示。

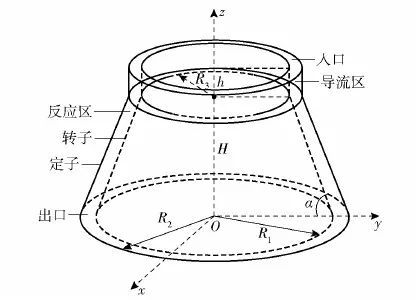
图1 旋转液膜反应器结构图Fig.1 The geometric shape of the rotating liquid film reactor

1.2 数学模型

反应器入口处静压与出口处静压都接近大气压，为简便计算，设入口和出口静压都等于大气压。测量临界流量时以水作为研究对象，满足不可压Navier- Stokes(N- S)方程，侧面边界条件为无滑移。考虑反应器的几何结构，在柱坐标下进行运算。此时控制方程可以表示成如下形式。

动量方程

(1)

(2)

(3)

连续性方程

(4)

且满足

式中，ρ、p和ν分别表示密度、压力和运动学黏性系数，ur、uθ、uz分别为流体速度在r、θ、z方向上的分量。设流体速度为u，则有u=urer+uθeθ+uzez，其中er，eθ，ez为单位向量。壁面的边界条件为

(5)

式中p0是标准大气压。

2 数值方法

基于N- S方程(式(1)～(4))以及边界条件(式(5))，使用有限体积法进行计算。从反应器中选择一个横截面，在柱坐标下求解临界流量。为了提高精度，在反应器壁面上引入边界层，并采用网格自适应以及自适应时间步长在Fluent上计算得到收敛的解。

模型采用压力入口和压力出口，在Gambit中基于四边形模型区域进行网格划分，边界层厚度的计算值不同，划分的网格数也有所不同，从几万到一百多万个不等。

在临界流量的计算中，模型的选取十分重要，模型选取又和反应器内流体的分类相关。因为反应器内流体属于旋转对称流，因此需要考察旋流数，其定义如下

(6)

式中，Gφ和Gx分别为角动量的轴向通量和轴向动量的轴向通量。当旋流数S> 0.5时，应使用雷诺应力模型，当S<0.5时，应使用k-ε模型。通过计算发现S<0.5，且采用k-ε模型中的Realizablek-ε模型稳定性最好，所以采用该模型进行计算。

反应器中边界处理对临界流量的计算很关键，δ是由雷诺数决定的，其经验公式为

(7)

其中雷诺数Re的表达式为

(8)

通常在距壁面距离为δ到y+=5之间有5层网格，在壁面距离为y+=5～30之间有20层左右的网格，使用边界层可提高对边界处小扰动的解算能力，增加模型精度。

反应器网格具体结构如图2所示。

图2 原反应器夹缝宽0.3 mm时的网格分段示意图Fig.2 A segment of the original mesh of the rotating liquid film reactor for a gap size of 0.3 mm

计算发现，使用可攀爬壁面函数与Realizablek-ε模型最匹配，因此选用该函数作为壁面函数，并在此基础上使用网格自适应以及自适应时间步长来提高模型的精度。

模型中的湍流作用会导致计算结果不收敛，需要分步计算提高结果的稳定性。首先计算未受旋转影响的流场情况，通过对流场预估来提高结果的精确性。然后使反应器转子开始旋转，只计算旋转产生的动量变化对流场的影响，同时要考虑到出现湍流的情况。结果稳定后忽略旋转对流场的影响，转而考虑其他方向速度对流场的影响，这一步也要考虑湍流的影响，结果稳定后联立方程并计算得到充分耦合的解。

3 数值模拟结果

3.1 算法的可靠性

图3是高17 mm、倾角75°的反应器在夹缝间隙d=0.3 mm、转速从1 000 r/min变化到5 000 r/min时的实验结果及数值结果对比，可以发现临界流量的数值解与实验值吻合较好，说明反应器模型和算法比较可靠。

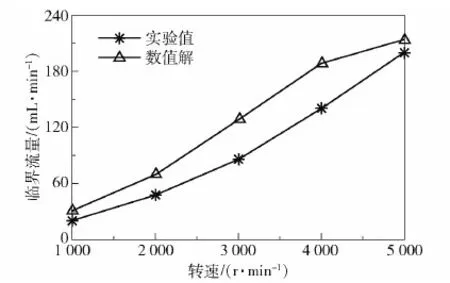
图3 夹缝0.3 mm时原反应器临界流量实验值与计算 结果比较Fig.3 Comparison of the experimental and the numerical results of the CVFR with a gap size of 0.3 mm

为了证明这种k-ε模型和算法适用于较广泛的倾角、夹缝和高度，通过新反应器模型进行验证，新反应器高45 mm，倾角85°。图4是该模型在d=0.15 mm时不同转速下的实验值与计算值对照。可以看出，临界流量的实验值与计算结果差距不大。结合图3可知，本文数学模型及计算方法对不同的反应器参数都有一定的适用性，综合来看可以运用该模型对不同高度的反应器进行研究。

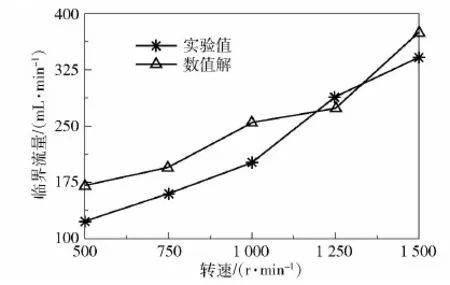
图4 夹缝0.15 mm时新反应器临界流量实验值 与数值计算结果比较Fig.4 Comparison of the experimental and the numerical results of the CVFR with a gap size of 0.15 mm

3.2 反应器高度对临界流量的影响

本节针对倾角85°、夹缝宽0.3 mm的新反应器模型，研究其入口半径不变，高度H分别为17 mm、24 mm、31 mm、38 mm、45 mm时临界流量随转速的变化情况，结果如图5所示。

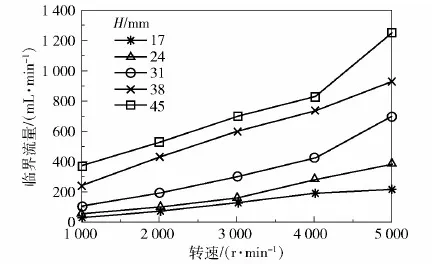
图5 不同高度下临界流量数值计算结果随转速 变化情况Fig.5 Numerical results of the CVFR with respect to the rotor speed for different heights

由图5可以看出，同一转速下，随着高度的增加，临界流量也随之增大，高度为45 mm和38 mm时反应器的临界流量增幅最大。

3.3 临界流量对反应器高度和转速的偏弹性

为了计算临界流量对高度的偏弹性，本文引入偏弹性的概念。假设临界流量是反应器高度H和转速Ω的函数，用f(Ω,H)表示。若使用坐标表示模型中转子的转速以及高度，则临界流量在点(Ω0,H0)处对H和Ω的偏弹性分别由式(9)、(10)计算。

(9)

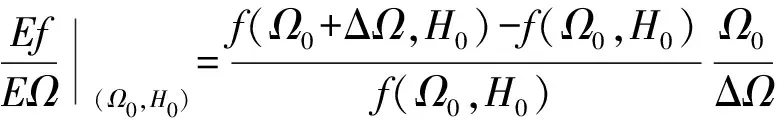
(10)

设ΔH=7 mm，ΔΩ=1 000 r/min，基于方程(9)、(10)计算图5中临界流量数值解对高度和速度的偏弹性，结果如图6和图7所示。

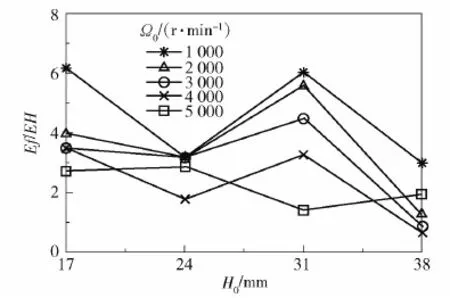
图6 不同转速下临界流量对高度的偏弹性Fig.6 Variation of the partial elasticity of the CVFR with height for different rotor speeds

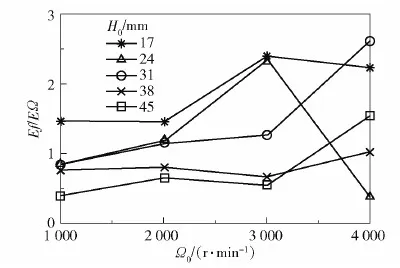
图7 不同高度下临界流量对转速的偏弹性Fig.7 Variation of the partial elasticity of the CVFR with rotor speed for different heights

从图6中可以看出，临界流量对高度的偏弹性在Ω0=1 000 r/min、H0=17 mm处达到最大值，为6.15；随着转速的增大，临界流量对高度变化的敏感度整体呈下降趋势。

从图7可以看出临界流量对转速的偏弹性在Ω0=4 000 r/min、H0=31 mm处达到最大值；随着高度的增加，临界流量对转速的敏感度整体呈下降趋势。

综合二者来看，临界流量对高度的敏感度整体上要大于对转速的敏感度，但是随着转速和高度的增大，对转速和高度的敏感性均逐渐减弱。

4 结论

本文提出了一种求解旋转液膜反应器临界流量的方法，并计算了在新、旧两种参数的反应器中临界流量随转速的变化情况，计算结果与实验符合较好，证明本文方法对不同高度、不同倾角、不同夹缝宽度以及不同转速的反应器都有一定的适用性。临界流量随反应器高度的变化情况及其对高度和转速偏弹性的计算结果表明，临界流量对高度的敏感性要大于对转速的敏感性。本文得到了对临界流量的初步计算结果，后续将对湍流模型进行一定的修正，使模型与反应器更契合，计算结果的精确度更高。