适用于低端激光雷达的优化Hector SLAM算法

苏易衡, 张奇志， 周亚丽

(北京信息科技大学 自动化学院，北京 100192)

0 引 言

建立环境模型并且确定自身位置是移动机器人在真实场景中应用所需的一项重要功能，实时定位与建图(Simultaneous Localization and Mapping,SLAM)关注的正是这一问题。随着SLAM研究的不断深入与激光雷达性能的提升迭代，建图与定位的精度已经基本满足室内、室外环境中的应用。例如基于改进的Rao-Blackwellized粒子滤波SLAM方法Gmapping[1-2]，利用激光雷达数据与高精度的里程计，在办公室环境具有较强的鲁棒性；此外基于Gauss-Newton方法的Hector SLAM，使用较少的运算资源，因此可用于无人机等装置在三维场景中建立环境模型[3-4]，但该方式对激光雷达的精度与刷新频率有很高要求，由于高性能的激光雷达价格昂贵，在许多场景中不太适用。

Hector SLAM是一种利用现代高精度激光雷达的数据，不需要依赖里程计数据的SLAM方法。该算法的一般处理过程为[5]：获取概率栅格地图、Gauss-Newton法扫描匹配、使用多分辨率地图避免陷入局部极小值。首先利用高精度激光雷达的数据，使用双线性插值算法获取连续的概率栅格地图；接下来继续获取雷达数据，使用当前帧与已有地图的数据构建误差函数，并用Gauss-Newton法得到最优解与偏移量；最后使用3种不同分辨率的栅格地图，避免匹配结果陷入局部极小值。

扫地机器人、家庭服务机器人[6]等应用场景中，经常由于成本控制或是设备老化等原因，所使用的激光雷达性能较低。本文在Hector SLAM研究的基础上，对前端进行了较为全面的优化，降低了算法的硬件应用门槛，消除了算法对高精度、高刷新频率激光雷达的依赖；同时解决了地图构建重影的问题，使数据噪声较大、刷新频率低的激光雷达在不借助里程计的条件下也能够完成SLAM任务。

1 算法实现

概率栅格地图是激光雷达描述真实世界的一种方式，经证明能对任意环境进行地图表述[7]。由于激光雷达数据的离散性，无法直接用于栅格地图的构建与扫描匹配，所以要先通过插值获得连续的概率栅格地图。

获取到栅格地图后，需要将后续到达的雷达数据进行扫描匹配，扫描匹配是将激光雷达扫描的实时数据与已有地图对齐的过程，原系统在这一步参考了图像对齐的方法构建误差函数[8]，使用Gauss-Newton法得到最为匹配的地图。该方式在雷达数据更新后，在上一时刻状态附近迭代出当前时刻的最优匹配，并计算得到位姿增量。Hector SLAM所建立的Gauss-Newton方程为:

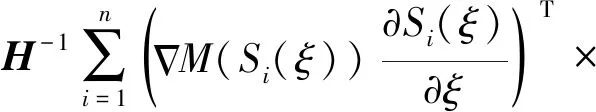
(1-M(Si(ξ)))

(1)

ξ=(px,py,ψ)T

(2)

(3)

(4)

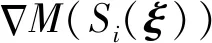
算法最后通过使用3种不同分辨率地图避免计算陷入局部极小值，得到最优解，并更新栅格地图数据。

针对上述算法分析，结合激光SLAM的具体应用场景，本文提出采用线段特征提取对雷达数据优化，使用双三次插值算法优化地图精度与梯度，最后通过图像相减与矩阵变换的方式获取激光雷达的运动模式，并优化关键帧更新机制以消除地图重影的问题。

1.1 激光雷达精度验证

为了验证方法的改良效果，首先对激光雷达精度进行验证，所用雷达见图1。该低性能激光雷达检测范围0.15～5 m，角精度1°，扫描频率仅为5～6 Hz。

图1 所用的激光雷达

本文获取3 s内激光雷达对同一入射角的12组重复测量数据，得到均值与标准差对激光雷达的检测精度进一步验证。具体实验过程如下:在相同实验条件下，重复测量以90°为入射角的目标点12次，距测量点正前方的距离分别为1、2和4 m，其中距离标准由高精度激光测距仪获得。得到A=[a1,a2,…,a12]，B=[b1,b2,…,b12]和C=[c1,c2,…,c12]3组数据。根据下式计算出均值和标准差:

结果如表1所示。

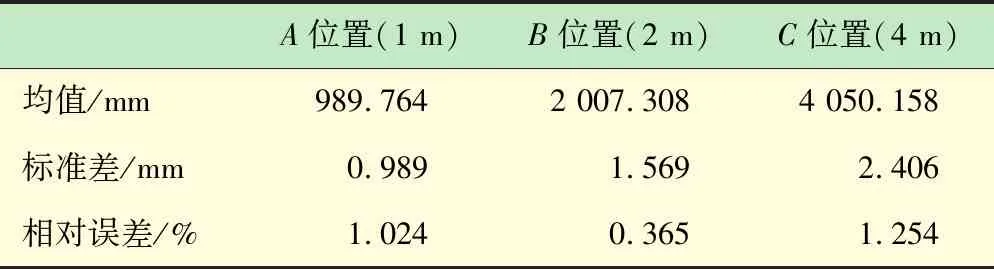
表1 激光雷达性能的测试结果

1.2 数据优化

由于低性能激光雷达的噪声较大，为了获取精度更高的建图与定位效果，本文通过2种方法对地图数据进行优化：利用地图中广泛存在直线特征数据，进行提取与拟合，减少雷达自身精度带来的误差；改变概率栅格地图的插值算法，提高地图的精度与连续性。

1.2.1 激光雷达直线特征数据的优化

在激光雷达检测的二维平面中，直线、转角等场景因为数据特征明显，经常作为路标储存并用于位姿图优化[9-10]。本文选择常见并且突出的直线特征，把一组激光雷达数据作为1帧图像矩阵来处理，通过概率霍夫变换提取并由最小二乘法拟合更新直线，对雷达数据优化来提高地图构建与匹配的精度。事实证明,对于检测距离较短的激光雷达，远端的直线数据得到明显的平滑。在后续的旋转判定实验中，能观察到直线特征数据中的明显噪点得到了消除。

在直角坐标系中可以用斜率和截距来表示1条直线，即

y=kx+b

(8)

式中,(b,k)表示直线参数空间的一个点，但由于存在k为无穷大的情况，通常将直线转换为极坐标系表示,

ρ=xcosθ+ysinθ

(9)

式中,极径ρ和极角θ为参数空间。则可得每一对(ρ,θ)与一条通过(x,y)的直线相关联，ρ、θ参数空间即为霍夫空间。如在直角坐标系中存在一条直线，则对应在霍夫空间中有多个点重合，根据设定的阈值可检测出直线[11]。由于霍夫直线变换的运算效率低且无法测得线段端点，不适合用于雷达数据处理，所以本文采用概率霍夫变换来检测直线。概率霍夫直线变换的3个步骤[12]：

(1) 把激光雷达数据储存为图像矩阵的形式，从图像中随机抽取一个数据点，映射到极坐标系并得到曲线。

(2) 当极坐标系里有交点满足最小投票数,即霍夫阈值，就得到了该点所对应的一条直线L。

(3) 获取图像在直线L上的点，连成线段并记录该线段的2个端点。删除该直线L上所有的数据点并返回步骤(1)，直到遍历图像中所有的数据点。

通过对概率霍夫变换相关参数的调整，可以保留或消除地图中部分障碍物信息，例如靠墙的桌腿，参数值可根据实际情况来设定。在得到图像中所有的直线数据以后，利用最小二乘法来获取最佳拟合直线。假设拟合直线方程为y=kx+b，对于任意样本(xi,yi)，根据以下公式得到误差：

e=yi-(kxi+b)

(10)

接下来计算偏差的平方和S，当S最小时,直线的拟合度最高，

(11)

至此完成对激光雷达数据的处理，对真实环境中的直线特征数据进行了优化。该方法减小了特征数据的噪声，并使远端较为稀疏的雷达数据得到明显的平滑。

1.2.2 优化概率栅格地图

在栅格地图中，每个栅格都由0、1数值来表示被障碍占据的概率，值越接近1表示该处有障碍的概率越大。因为激光雷达获取的数据是离散的，而系统需要构建连续的栅格地图，并且扫描匹配时偏导运算也需要数据具有连续性。由于低性能的激光雷达角精度较低，有效数据量少，故使用双三次插值算法来获取连续性更高的概率栅格地图，以减少系统噪声、提高后续使用Gauss-Newton法进行地图匹配时的准确性[13]。

双三次插值算法要选取插值点周围的16个采样点进行加权[14]，假设插值点位于(i+u,j+v)，则(i,j)为插值点的整数部分;u、v分别是插值点在X、Y轴上的小数部分。算法选取的是以点(i-1,j-1)到(i+2,j+2)为对角线的矩形网格中的16个采样点数据：

(12)

算法首先构造用于对临近值加权的双三次插值核函数S，

S(x)=

(13)

式中,参数a在本系统中选值为-0.5[15]。而

f(i+u,j+v)=ABCT

(14)

是双三次插值的计算方法，等号左侧为算法得到的插值数值，等号右侧为计算过程，运算后可以得到插值点的数值。其中:

A=

(S(1+u)S(u)S(1-u)S(2-u))

(15)

C=

(S(1+v)S(v)S(1-v)S(2-v))

(16)

由于改变了栅格地图的插值算法，Gauss-Newton法迭代时使用的地图梯度也同时得到了优化。需要对式(14)求X、Y轴方向的偏导:

∂f/∂u≈A′BCT

(17)

∂f/∂v≈ABC′T

(18)

把u、v代入

(19)

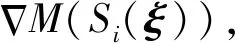
1.3 地图重影的解决

激光雷达的数据优化可以有效减少系统噪声，获取精度更高的地图数据，但是地图构建时的重影问题并不能得到有效解决。低性能雷达在建图过程中经常会发生重影的问题，是由于雷达数据更新慢、连续性差导致的帧间偏移过大，数据被系统判定为关键帧更新至地图。为了确定重影发生的原因，对激光雷达的运动模式进行分析。激光雷达在移动机器人上具有3个自由度，分别为X、Y轴上的平移与绕Z轴的旋转，也就可以将其移动模式归结为平移与旋转两种。经过测试，低性能激光雷达在平移时地图不会出现重影；但在旋转时造成的地图重影问题十分严重，这就需要对旋转运动进行判定，达到消除重影的目的。本文根据平移与旋转时，激光雷达数据的变化特性，应用图像处理中常用的方法即图像相减与矩阵变换，来确定激光雷达的运动模式，最后优化关键帧的发布机制，消除了地图重影的问题。

1.4 运动检测

在概率霍夫变换的步骤中，已经以二值图像的形式存储了雷达数据。本文应用图像相减的方法，将当前时刻的雷达图像与上1帧数据图像相减，再计算差值图像中非零数据点的个数，就可以判断出激光雷达是否运动。因为低刷新频率的雷达在旋转运动时会产生地图重影，所以当检测出雷达发生运动后，需要对旋转模式进一步判定。当没有检查到位移时，不进行旋转判定，以节省计算资源。

1.5 旋转判定

激光雷达发送的数据为(ρ,θ)形式的极坐标数据，即角度与距离数据。当激光雷达发生旋转时，周围障碍物与激光雷达之间的距离数据不会有较大的抖动，改变的只是障碍物相对激光雷达的角度。假设激光雷达上1帧数据为(ρ,θ)，当前帧较上1帧绕正方向旋转了α°，则理想情况下新的雷达数据可以表示为(ρ,θ-α) 。根据激光雷达数据的该特性，便可求出其旋转角度。

当系统识别出激光雷达的运动模式为旋转时，将旋转前的雷达数据传递至扫描匹配即可；同时可以在系统中增加适当的延时，避免机器人旋转抖动造成的误差，增加系统鲁棒性。在引入旋转判定机制前，激光雷达的旋转会造成如图2所示的地图重影；优化判定机制后，雷达正常旋转造成的干扰已经消除，如图3所示。实验验证该方法可以消除激光雷达旋转造成地图重影的问题。

图2 优化前旋转雷达造成重影

图3 优化后消除旋转带来重影的问题

2 实验结果

针对本文提出的优化方法，通过移动机器人搭载低性能激光雷达，在大小为7.2 m×5.0 m的实验环境进行验证。实验环境与机器人平台如图4、5所示。两次实验中，机器人均以0.3 m/s的速度绕场地运行，旋转的角速度约为1 rad/s，且所建立的地图分辨率均为5 cm。

图4 实验环境

图5 机器人平台

首先机器人使用未加入旋转判定的算法，在平移运动时能够正常建图，但在转弯处出现地图重影的问题。机器人的定位出现误差并且不能修复，无法得到正确的地图，如图6所示。接下来使用完整的优化算法，机器人在4个转弯处都能保持正确的建图，地图出现重影的问题已经解决，见图7。使用本文算法所构建的地图可以准确地反映地图中挡板、垃圾桶、墙面等有效信息，减少了地图噪声并且明显平滑了地图中的直线特征数据。

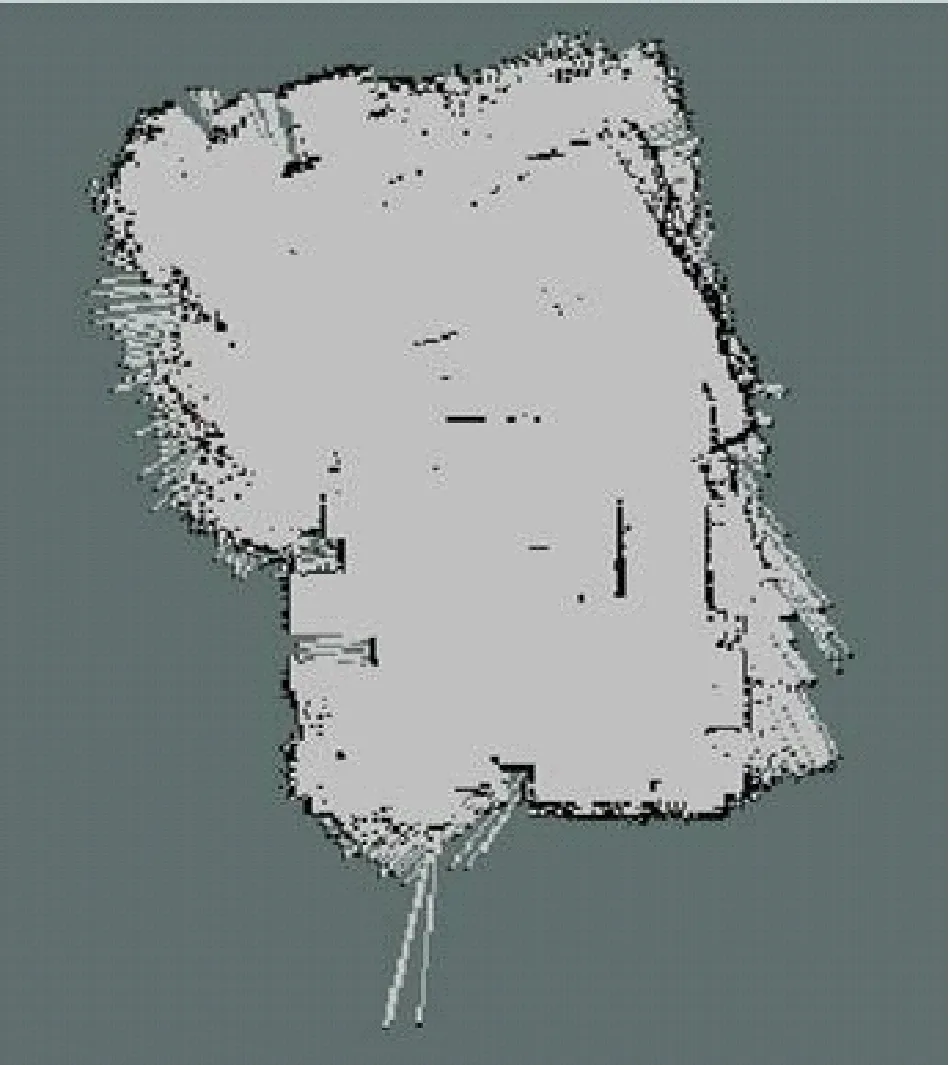
图6 机器人的旋转造成地图重影

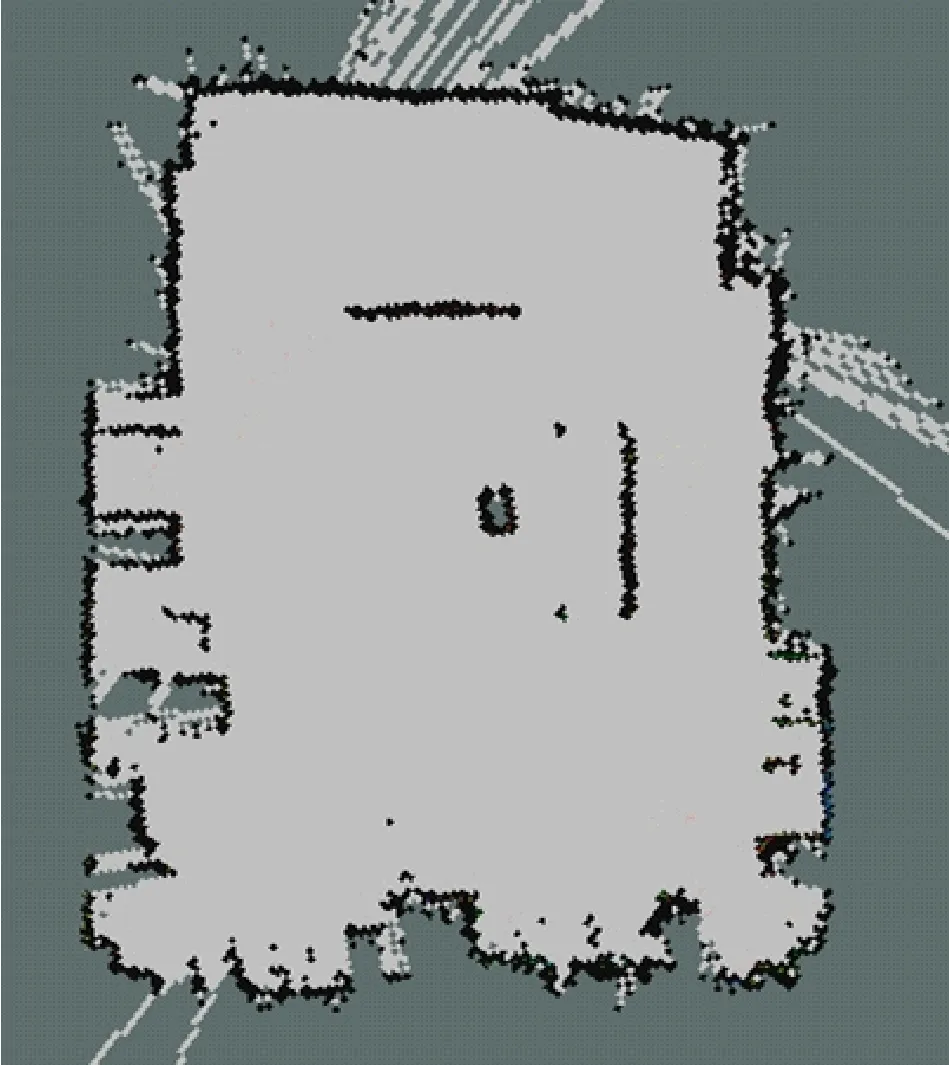
图7 优化后常规的旋转不再影响建图

3 结 语

基于本文优化后的Hector SLAM算法，使用低成本的激光雷达也可以得到准确的地图数据并消除了地图重影的问题，同时在构建全局地图时直线特征得到明显平滑，有效减少了系统噪声。由于低性能激光雷达的数据质量较低、每帧数据间隔较长，为了提高SLAM算法的实时性与准确性，可以在系统中引入里程计并使用位姿数据，实现SLAM的后端优化与回环检测，达到优化建图效果的目的。