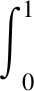一种图像清晰与模糊的判别方法
傅志中, 王琦艺, 李晓峰, 徐 进
(1.电子科技大学 信息与通信工程学院,成都 611731;2.昆明物理研究所,昆明 650223)
0 引 言
在实际应用场景中,由于人为操作原因或拍摄场景恶劣,传感器失真等原因都会导致图像质量降质,其中一种最常见的图像降质为图像模糊[1]。当前大量图像处理应用及实验教学应用中,如图像分割[2]、目标提取与识别[3-5]等,都假设待处理图像是清晰的。文献[6-7]中研究了运动原因导致图像模糊的运动去模糊技术,实现了模糊图像的清晰化处理,为后续图像处理任务提供清晰化图像。但是,由于模糊函数的病态特性,损失的信息不可恢复,基于算法复原的图像清晰度仍然不能满足应用需求。因此,迫切需要对图像的模糊与清晰程度进行预先判定,剔除模糊图像,仅保留清晰图像用于图像处理任务,提高图像处理任务性能。
图像模糊检测方法可大致分为三类:提取图像特征进行阈值设定,建立评价模型对图像进行评估,利用图像抠图方法定位模糊区域。基于上述3类方法的模糊判断有:段兴涛等利用图像的四向差分特征,用阈值法判断模糊图像的存在;文献[8-10]中利用图像的边缘梯度分布的拟合标准差、Haar小波分解的边缘类型判断出图像边缘的模糊程度;Su等[11]提出利用图像像素奇异值之间的关系,直接实现图像的模糊区域定位。
近几年又发展出了基于DA的模糊图像识别方法[12],该方法基于LMDR度量学习,提高了模糊图片的识别性能,但其需要前期大量的样本进行学习训练,过程繁琐且不能给出图像模糊程度的定量描述。文献[13]中提出了利用频率系数统计特征、峰度值、颜色饱和度三方面作为图像特征来进行图像模糊判定,该方法针对灰度图像将失效并且特征建立过程繁杂。上述模糊识别算法均涉及较多的图像特征提取与建模过程,在很多恶劣场景下,这些特征并不能被有效和准确地提取。
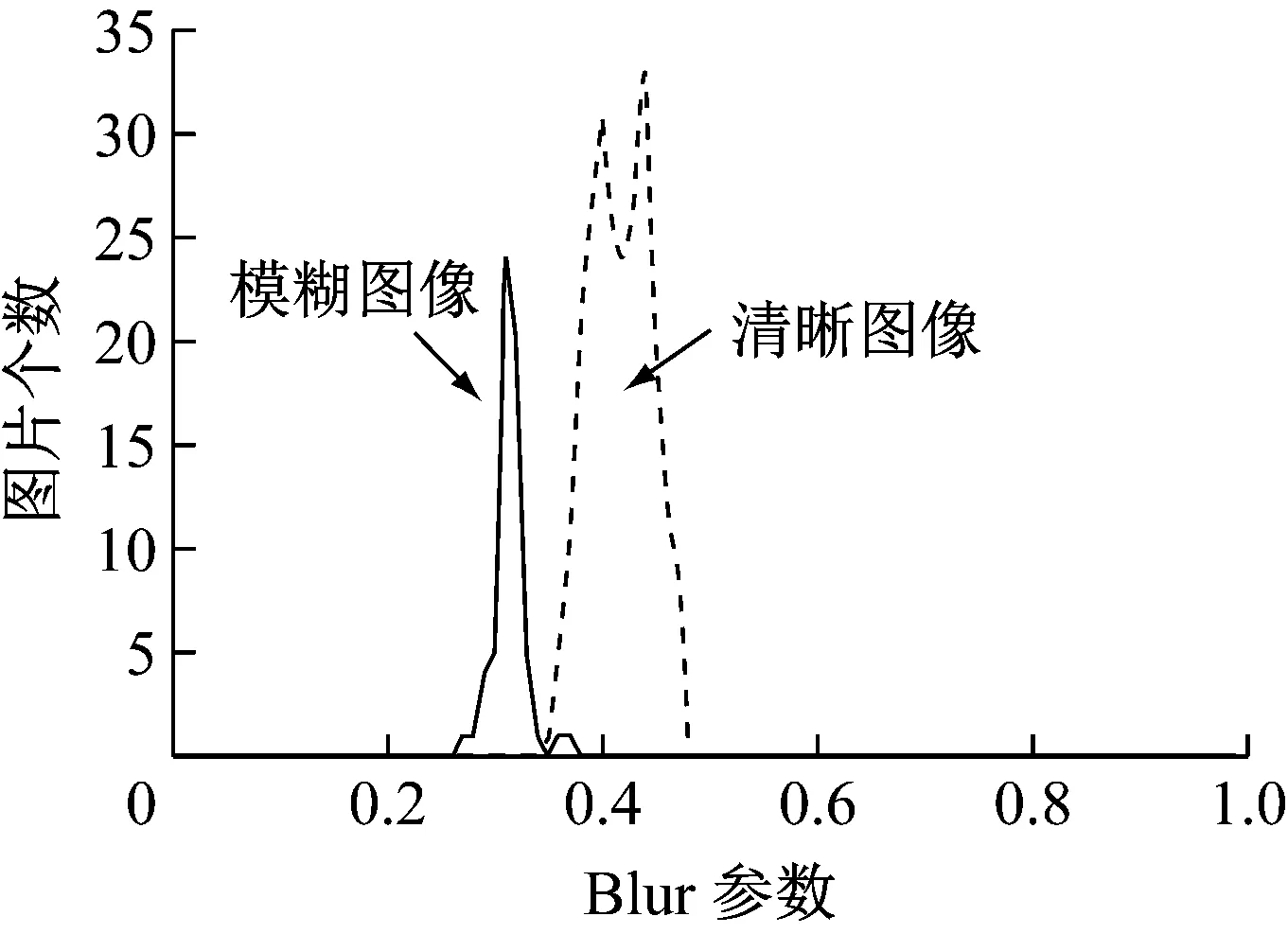
本文提出了一种基于图像频谱分段信息的图像清晰与模糊判别与衡量方法。根据图像频谱分布的统计特性可对模糊与清晰图像进行分类,同时给出模糊程度的定量描述。
1 图像的频谱分析
对灰度图像I(x,y)∈{0,1,…,255},若尺寸为M×N,其二维傅里叶变换定义为[14]
(1)
为了更直观地显示图像在频域的能量分布情况,通常要将图像的傅里叶变换结果进行搬移,将原点移至中心,这一过程可通过对原始图像乘以(-1)x+y实现。同时,因为傅里叶变换结果为复数,因此还需对结果取绝对值,得到的二维图像的频谱如下:
S(u,v)=abs(F(-1)x+yI(x,y)(u,v))
(2)
需要指出的是,因为图像为二维实信号,因此,其中心化的傅里叶频谱是关于原点中心对称的[15],如图1所示。
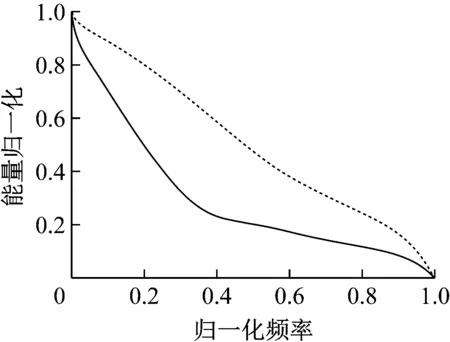
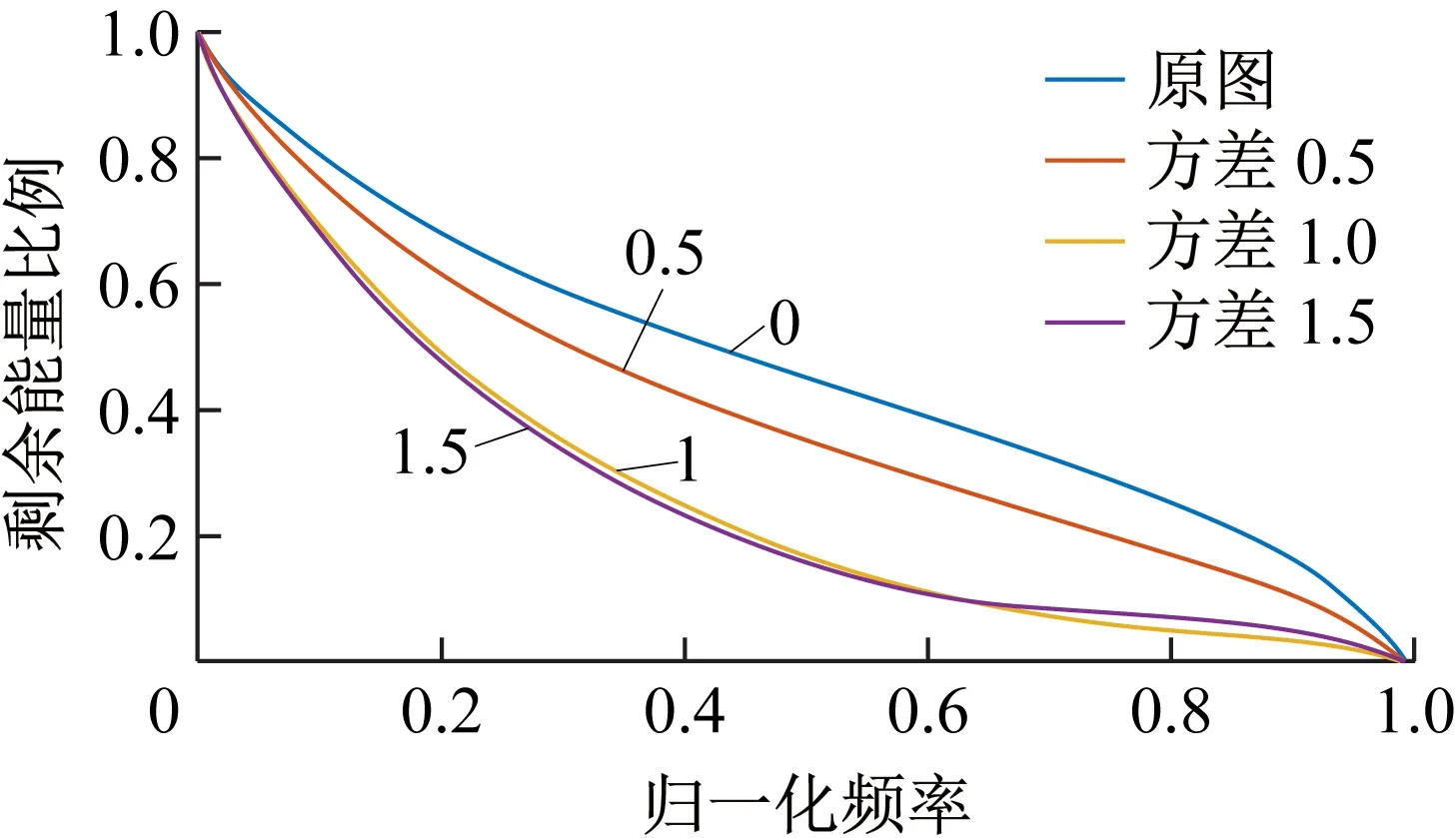
信号频谱的低频部分对应时域中变化变化缓慢的部分,即图像的平滑区域;反之,高频部分对应图像的边缘,纹理等高频信息。模糊图像的边缘与纹理等高频信息受模糊影响被削弱,而平滑区域等低频信息基本不受影响。清晰图像因为有丰富的边缘、纹理等高频信息,因此其频谱能量在高频区域分布多于模糊图像。

原图

中心化傅里叶频谱
图1 原始图像与傅里叶频谱
2 基于频谱分布的模糊判定方法
基于模糊图像与清晰图像在频谱分布上的差异特性,本文提出了一种判别模糊图像与清晰图像的方法,其流程如图2所示。
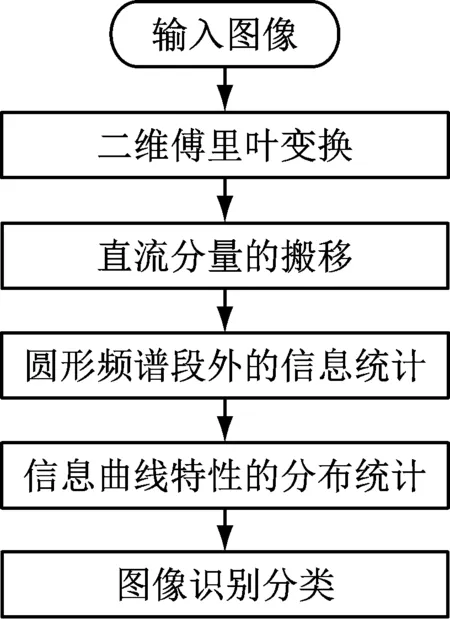
图2 算法整体流程图
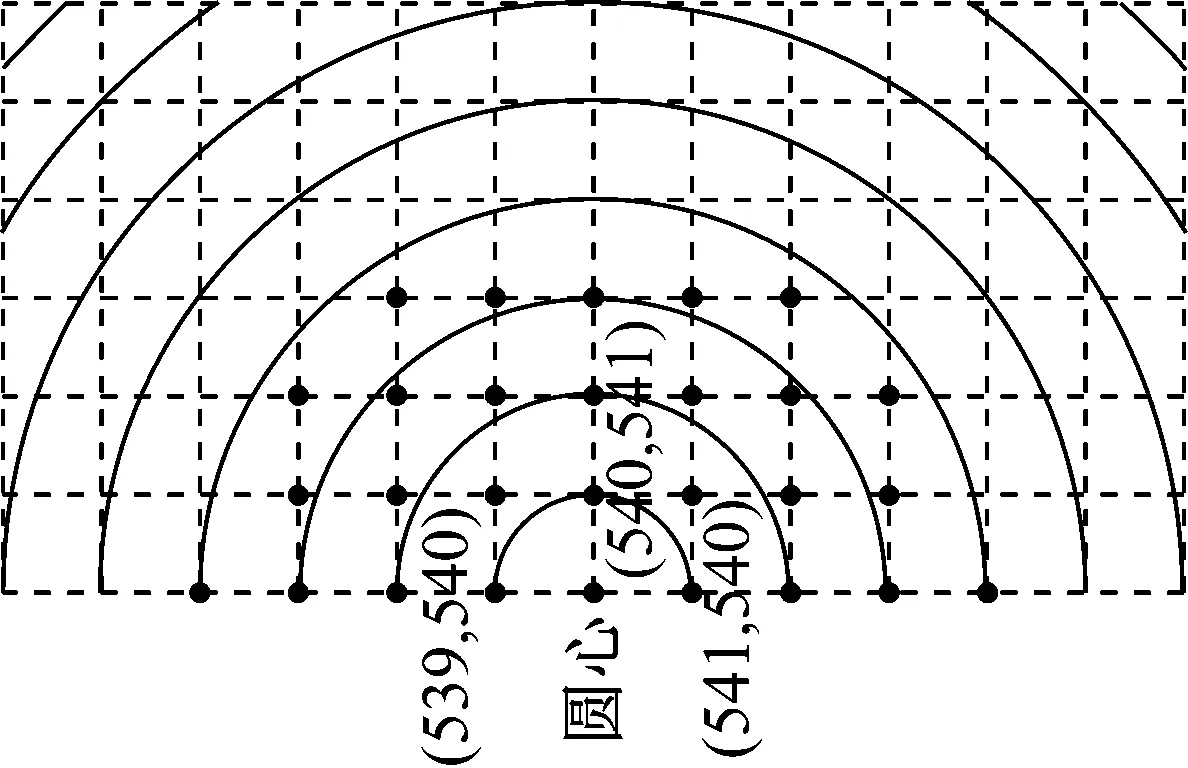
首先对灰度图像进行傅里叶变换得到其中心化的频谱信息,随后取以原点为圆心,半径从1逐渐增大的圆形区域,计算这些圆形区域外的平均归一化频谱能量,得到频谱能量分布曲线。通过统计曲线下部的积分面积即可求得归一化的模糊程度衡量参数。基于不同具体场景,设定不同阈值即可在该场景下有效的区分模糊与清晰图像。
2.1 圆形段外频谱信息统计
针对中心化之后的图像频谱,对频谱分布进行了统计。以一幅大小为a×a的图像为例,其中心化之后的频谱为一个a×a的实矩阵,由实信号频谱的对称特性可知,只需统计中心点一侧的频谱分布即可。为统计该频谱分布,首先定义以频谱中心原点为圆点以r为半径的圆形区域:
C(r)=
(3)