修正的阿伦方差对调相闪烁噪声的抑制

北京东方计量测试研究所，北京 100086

频率稳定度是描述原子钟稳定性的重要指标，原子钟频率稳定度的算法同时也影响着原子钟性能的评估。但是，无论在何种测量环境下，噪声对频率稳定度测量的影响都无法完全消除，只能采取有效措施进行抑制。一般情况下，若想更有效地消除噪声，需要更长的测量时间；但在同等测量时间内，怎样更有效地降低噪声对测量的影响则成为时间传递的关键。时间传递的本质就是传递过程中噪声本身的测量。

原子钟的溯源问题可以利用卫星远程共视时间比对法解决，通过共视时间比对数据可以得到原子钟的各项性能指标，包括频率稳定度。在对频率稳定度进行评估时，普遍采用阿伦方差。但是，与阿伦方差相比，修正的阿伦方差有其本身算法的优势，可以有效地抑制噪声尤其是调相闪烁噪声对测量的影响。本文通过卫星共视时间比对法，利用实验室主动型氢原子钟与原子时标国家计量基准进行时间比对。通过两地钟的时间差数据对频率稳定度进行评估，并分析了修正阿伦方差抑制调相闪烁噪声的机理。

1 原子钟噪声特性

原子钟噪声的数学模型定义原子钟t时刻的时差值为x(t)，则原子钟的时差模型可表示为[1-2]：

(1)

式中：a0为时刻偏差；a1为频率偏差；a2为频率漂移；ξ(t)为噪声项。公式(1)称为原子钟时差的多项式模型，是通用的原子钟时差数据的描述方法。时刻偏差一般指本地钟与参考时钟的秒脉冲1脉冲/s的相位差;频率偏差指时间偏差的一阶线性拟合的系数；频率漂移率是频率偏差随时间单调变化的线性率；噪声项是扣除原子钟的系统性变化(即多项式模型)外的各类噪声的综合。对于其中的噪声项，原子钟的噪声可用5种独立的随机过程表示[3-4]，即：

ξ(t)=z-2(t)+z-1(t)+z0(t)+z1(t)+z2(t)

(2)

式中：zα(t) (α=-2，-1，0，1，2)代表5种独立的噪声过程：调频随机游走噪声(Random Walk FM，RWFM)、调频闪变噪声(Flicker FM，FFM)、调频白噪声(White FM，WFM)、调相闪烁噪声(Flicker PM，FPM)、调相白色噪声(White PM，WPM)。但是并不是每个原子钟在测量过程中都一定含有上述全部5种噪声，一般情况下，只是2～3种噪声在起主要作用。

2 修正的阿伦方差降噪机理

由于噪声的非平稳性质，尤其是“闪烁噪声”的存在，使得用标准差表征频率稳定度时，结果将随采样数的增加而发散[5-6]。为了克服闪变噪声随时间变化出现的非平稳问题，D.W.Allan博士提出采用双采样方法对原子钟的频率稳定度进行评估，即Allan方差[7]。

(3)

式中：xi为时差序列；N为时差采样数；τ0为采样间隔。Allan方差通常以均方根的形式表示[8]，ADEV或σy(τ0)。

与阿伦方差相比，修正的阿伦方差的均方根即MDEV的表达式如下[9-10]：

(4)

式中：xi为时差序列；N为时差采样数；τ0为采样间隔；m为在N采样时差数内的采样数。

Allan方差可以识别不同的噪声类型[11]，对不同噪声的表征是通过不同的取样时间体现的[12]，即在一定的取样时间内对应着一定的噪声过程。在一定的取样时间内，噪声主要由几种噪声共同贡献，但是实际上，无论采样时间长短，5种噪声都是共同作用在整个测量过程中的，只是噪声系数的权重有所不同。而调相闪烁噪声附加在信号上，引起信号的相位调制，它对短期频率稳定度影响较大。因为附加噪声频谱较宽，高频分量多样，所以这种噪声频率变化很快。随着取样间隔的增加，这种起伏就会被平均掉。对于双采样的Allan方差而言，当取样时间大于最小采样间隔时，很多的采样数据就没有参与运算，取样时间越大，未参与运算的时差数据就会越多，频率稳定度的评估过程也就不能很好地抑制调相闪烁噪声的影响，但MDEV却可以很好地解决这个问题。

由式(4)可知，MDEV在计算频率稳定度时与ADEV不同，MDEV用相邻数据以m为长度的采样数据的平均值作为当前计算的时差值，然后向下平移一个τ0(最小采样间隔)的采样数据，所有的采集数据都会参加运算。这样的缺点是大大增加了运算量，且取样总数也会相对减少。但对于频率稳定度而言，MDEV可以视为对所有时差数据进行了平滑，对于高频的噪声能够起到很好的滤波效果。式(4)中的m可以理解为平滑窗口的大小，随着m的增大，平滑窗口也增大，也就是取样数增大。但当平滑窗口过大，高频分量的噪声信号的平滑效果会降低，噪声的抑制也就不再明显。从这种角度讲，MDEV也可以看成一种短期频率稳定度评估中数据加窗平滑的降噪方法，高频噪声信号在时域短窗口的平滑中会被平滑掉，对于频域而言就是被滤波掉，这就是MDEV对短期频率稳定度评估优势的机理。

3 试验数据验证与分析

试验数据利用主动型氢原子钟，远程时间比对基准以原子时标国家计量基准即UTC(NIM)的时间频率信号作为参考。通过两地原子钟同儒略日的CGGTTS数据处理得到氢原子钟与UTC(NIM)的时间偏差，通过对两地钟时间差数据的解算可以得到平均相对频率偏差、频率稳定度等相关性能指标。试验采用了共21天的共视时间比对数据，利用这21天的共视时间比对数据得到的ADEV频率稳定度与MDEV频率稳定度的结果如图1、图2所示。

图1 阿伦方差解算的频率稳定度Fig.1 Frequency stability of Allan variance

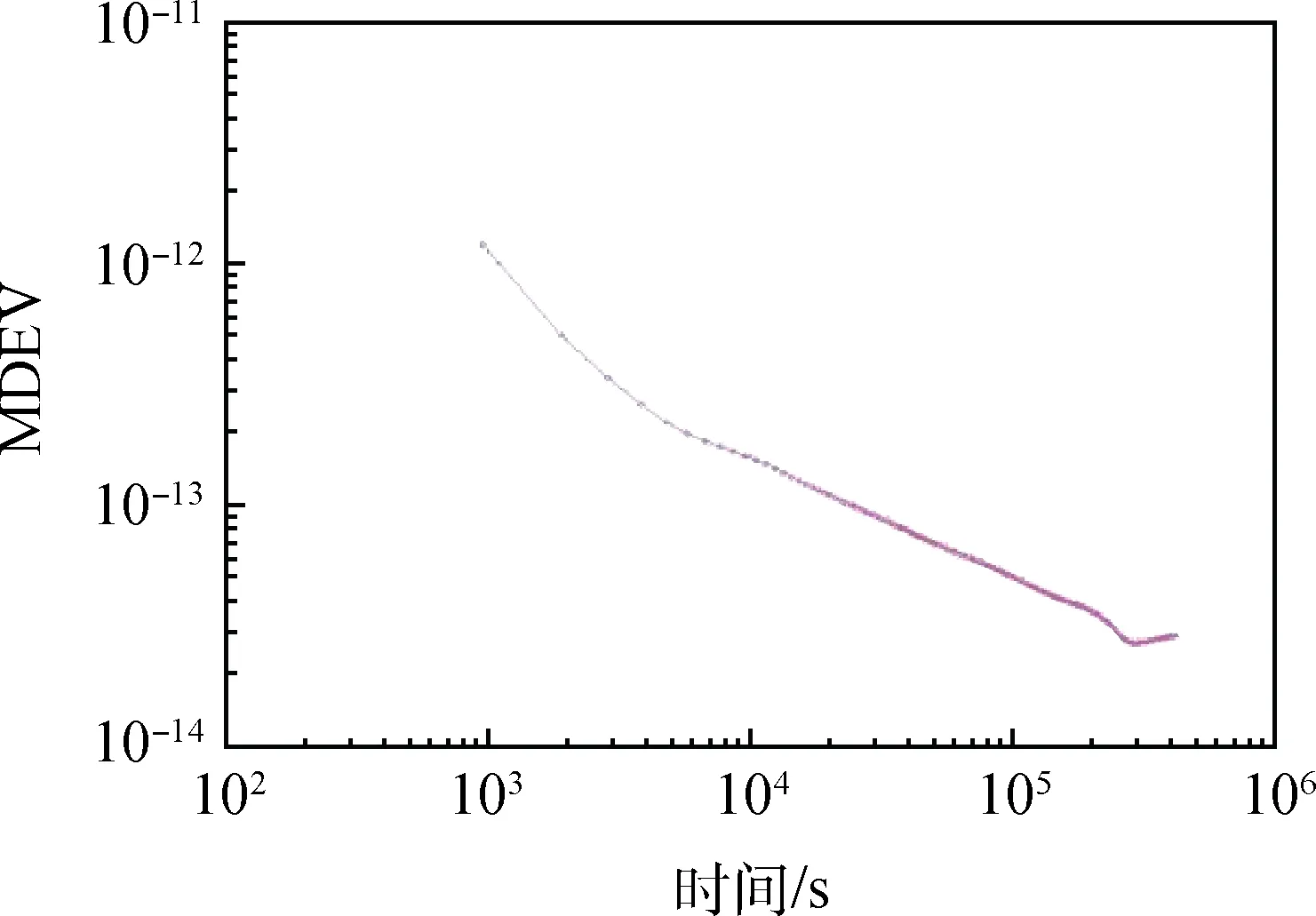
图2 修正阿伦方差解算的频率稳定度Fig.2 Frequency stability of modified Allan variance

比较图1与图2不难发现，同是频率稳定度的计算，MDEV具有更好的数据平滑效果，在频域范围内也体现了MDEV滤波的效果。MDEV对于上述的5种噪声类型的抑制情况可以通过时域噪声模型进行验证分析。在测试环境稳定的情况下，各个随机项可认为是统计独立的随机过程，因此原子钟的时域噪声模型可表示为[13]：

(5)

基于时域的相位噪声理论，Allan方差噪声模型如下[14]：

(6)

式中：τ为取样时间；h-2、h-1、h0、h1、h2为各噪声系数;fh为频率上限。在已知了5个随机噪声项在典型时间间隔下的Allan方差值之后，通过最小二乘法拟合Allan方差的双对数曲线，从中可以求解出各个随机项的系数[15-16]，具体解算的系数结果如表1所示。

表1 ADEV计算的噪声系数

由表1可知，5种噪声类型中，调相闪烁噪声的权重是最大的，即这种噪声对于测量过程的贡献是最大的，这也是Allan算法缺陷所至。现将表1计算中的5个频率稳定度值用MDEV计算出的频率稳定度代替，时间间隔不变，就可得到MDEV相对于ADEV在5种噪声系数下的噪声系数，见表2。

表2 MDEV计算的噪声系数

从表1和表2的比较可以看出，无论是ADEV算法还是MDEV算法，在对频率稳定度的评估方面，调相闪烁噪声(α=1)的贡献都是最大的。对于ADEV算法而言，h1系数的贡献量相对于其他系数的权重更大。而利用MDEV解算得到的h1系数有明显变小的情况。与其他噪声系数的比例关系对比后不难发现，调相闪烁噪声的作用仍为主导。也就是说，在频率稳定度分析中，MDEV算法无法改变主要噪声作用的趋势，但会降低调相闪烁噪声对频率稳定度测量的影响。

4 结束语

针对原子钟频率稳定度的评估方法，本文提出了MDEV对于噪声抑制的机理。试验结果表明，在时域范围内，短期频率稳定度测量中的主要噪声包括调频白噪声和调相闪烁噪声。而MDEV对于调相闪烁噪声的抑制效果明显优于ADEV。对原子钟进行远程时间频率溯源及传递中，MDEV更适用于频率稳定度的评估。本文对实际的应用具有一定的价值。