一种基于信号合成的无线电干涉测量方法
谢剑锋 陈略 任天鹏 韩松涛 王美
1. 北京航天飞行控制中心,北京 100094 2. 航天飞行动力学技术国家级重点实验室,北京 100094
深空探测距离的增加对测控通信系统的测量精度和数据传输速率等提出了更高的要求,而目前我国深空探测网性能尚无法满足。当前提高测控频段、增大天线口径、提高发射功率以及先进编码和降低系统噪声等技术无法满足日益增长的深空测控任务需求。以火星探测任务为例,传输1 Mbit/s的数据,需要80 m的天线(由NASA任务的参数计算得到)[1]。但是,天线口径越大波束越窄,探测器下行信号的捕获越难,伺服驱动也越困难。天线组阵技术通过对多个阵元信号合成等效为一个大口径天线,具有较高的灵活性和较强的鲁棒性,成为提高深空探测测控通信能力的主要途径,在国外深空探测任务中得到了较为广泛的应用。
天线组阵技术最早由美国喷气推进实验室(JPL)于1965年提出应用于深空探测,先后经历了三个发展阶段,实现了从非专用阵到专用阵、从本地阵到异地阵、从基带合成到全频谱合成的转变,在多次深空探测任务中将数据传输率从kbit/s量级提高到Mbit/s量级,并挽救了伽利略任务(主通信天线失效),具备应急测控能力[2]。天线组阵技术是将深空探测距离推进到火星、木星等太阳系内各大行星的一个重要支撑。
目前美国宇航局深空网每个深空站都配有一个4×12 m的天线阵,用以支持其重返月球任务,并在2010~2030年深空网发展规划中大量使用小口径(10 m级)天线组阵。欧空局(ESA)近年来也加大了深空天线组阵方面的研究,拟采取天线组阵的方式将现有35 m站的G/T(天线增益与系统温度的比值)值提高10 dB。
国内从2005年开始对深空测控通信天线组阵技术进行研究,目前在理论研究和试验验证方面都取得了较大进展。在理论研究方面,针对JPL提出的经典相关算法(Simple、Sumple、Eigen等)开展仿真分析和改进研究[3-5],以及采用Matlab/Simulink、QT工具开发天线组阵仿真平台,为天线组阵建设提供理论仿真支持[6-7]。
在试验验证方面,开展了组阵系统设计、合成基带原理样机的研制以及对星演示试验等。2010年,北京跟踪与通信技术研究所、中电科54所、装备学院、北京遥测技术研究所等联合建立我国天线组阵试验系统,并开展了对CE02卫星等验证试验,合成效率优于91%[8]。2011年,中电科10所对位于L2点的CE02卫星开展了下行微弱信号实时合成试验,合成效率超过95%,数据传输率达到1.5Mbit/s[9]。上海天文台、北京遥测技术研究所等单位将天线组阵技术应用于CVN(China VLBI Net, 中国VLBI网),提出了长基线天线组阵,并开展了深空探测遥测信号合成试验,合成后遥测信号信噪比提高了约4 dB[10]。
综上所述,国内外天线组阵技术研究及深空探测任务实践表明,天线组阵技术的研究重点集中在如何改善航天器数据传输率方面,而利用该技术改善无线电测量精度的研究未见报道。这可能的原因是目前深空探测任务中一般有干涉测量信标信号,信号功率相对较强,基本满足无线电干涉测量精度要求。但基于信号合成的无线电干涉测量方法具有两个方面的优势:1)在当前信号功率下,可以达到更高测量精度;2)在后续信号功率减弱或深空探测距离进一步增加时,保证深空探测精度。
鉴于此,本文提出了一种基于信号合成的无线电干涉测量方案,分析了信号合成对干涉测量随机精度的改善性能;根据深空探测DOR(Delta of Range, 距离差分)信标信号特点,提出了适用于无线电干涉测量的信号合成算法,最后通过试验数据处理和蒙特卡罗仿真,分别对单音信号和DOR信标进行信号合成,验证了信号合成对差分相位估计精度和无线电干涉测量时延估计随机精度的改善。
1 基于信号合成的无线电干涉测量方案
1.1 方案原理及分析
假设无线电干涉测量系统有两个测站,每个测站由N个阵元组成,如图 1所示。首先对每个测站N个阵元的接收信号进行信号合成,然后将合成信号传输至无线电干涉测量相关处理中心,最后通过相关处理得到时延观测量,实现无线电干涉测量。该无线电干涉测量系统的等效基线为两个测站天线阵合成信号相位中心的距离。
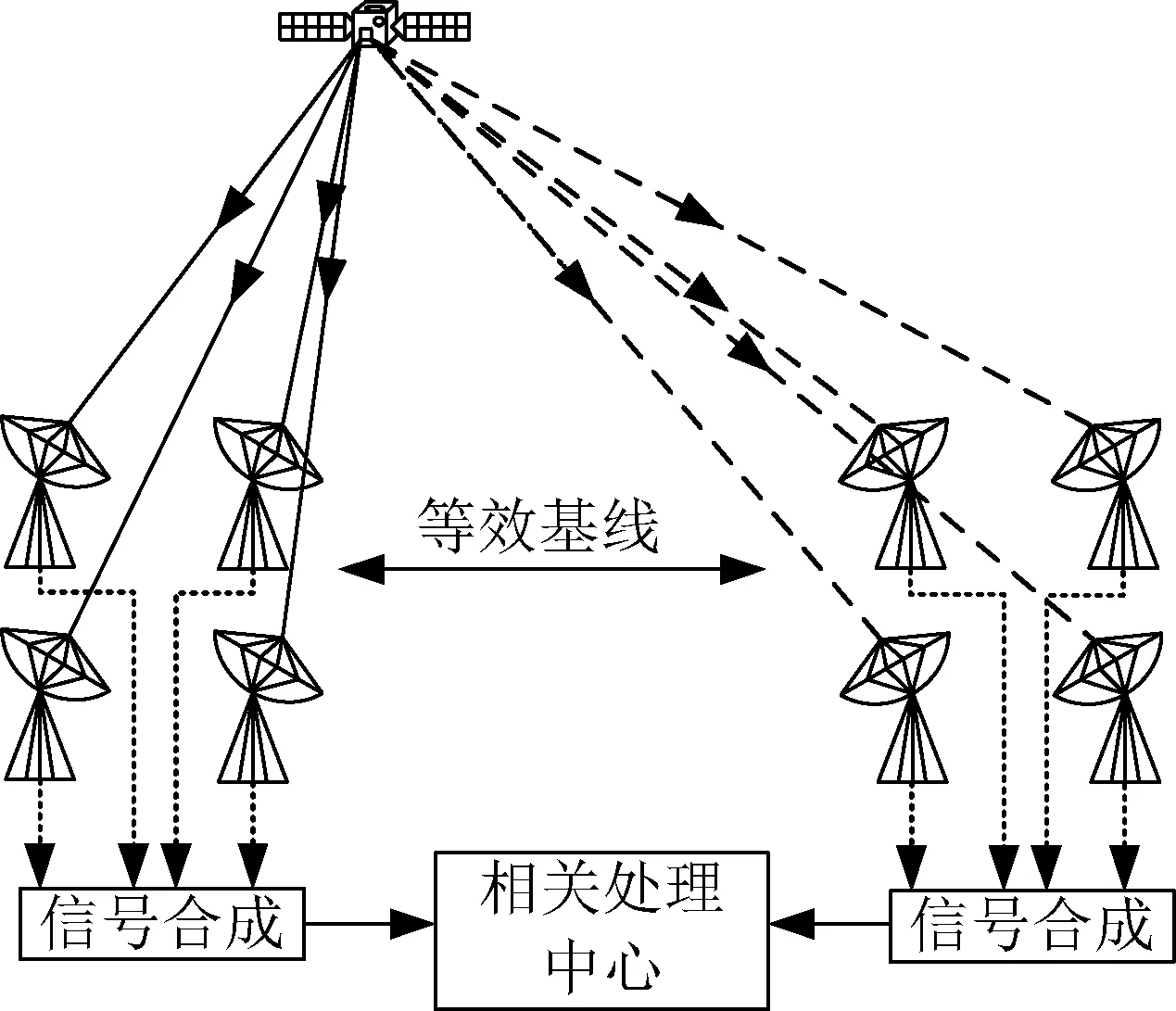
图1 基于信号合成的无线电干涉测量系统示意Fig.1 The scheme of interferometry based on signal combination
假设每个测站N个阵元的接收信号信噪比为SNR(实际中各阵元SNR可能存在差别),信号合成效率为η(合成效率定义为实际合成信号信噪比与理想合成信号信噪比的比值),则测站合成信号实际信噪比为:
SNRc=ηN·SNR
(1)
在无线电干涉测量中,载波或DOR信标信号等均可建模为正弦信号,干涉测量精度与载波或DOR信标信号的相位精度直接相关。相位估计精度可如式(2)表示,其中L为相关长度,SNR为信号信噪比。

(2)
通过天线组阵信号合成,合成信号的信噪比有所改善,那么相应的相位估计精度也有所改善。结合式(1)、(2),可得相位估计精度改善幅度为:

(3)
式中:σφC、σφRef分别为合成信号和参考信号的相位估计精度。
下面分析信号合成对无线电干涉测量精度的影响。假设无线电干涉测量系统有一条基线、两个测站A和B。其中,A站含有M个天线,B站含有N个天线;航天器下行信号两个侧音f1和f2,两个测站各天线接收侧音信号相位分别为φAm_1、φAm_2,m=1,2,…M,φBn_1、φBn_2,n=1,2,…,N,则由干涉测量原理,由两个测站侧音信号的差分相位可得时延估计:
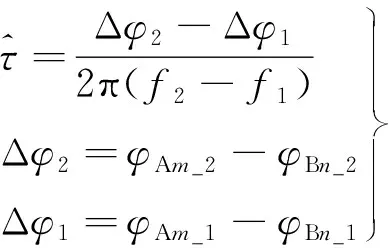
(4)
则进一步可得时延估计误差:

(5)
假设所有天线指标一致,接收性能相同,则可认为所有天线接收信号的相位随机误差相同,时延估计误差可简化为:

(6)
其中,σφAm_1=σφAm_2=σφBn_1=σφBn_2=σφ。
假设在干涉测量中,两个站分别对所有天线接收信号进行合成,然后再进行相关处理。则由式(3)可得信号合成后A、B两站相位估计误差σφACi,σφBCi为:

(7)

(8)
结合式(3)可得信号合成后,时延估计随机误差改善幅度为:

(9)
1.2 信号合成算法改进
合成信号具有与参考信号相同的相位特性是天线组阵技术应用于干涉测量的前提。在众多信号合成相关算法中,Simple相关算法选择某个天线接收信号作为参考信号,其余信号与参考信号相位对齐、加权叠加,因此合成信号与参考信号具有相同的相位特性。但由于Simple算法只需各个阵元信号与参考信号进行一次相关即可实现相位延迟估计和信号合成,未充分利用各阵元间下行信号的相关性,合成效率较低。
Sumple相关算法通过虚拟、流转的“参考信号”与各阵元信号进行相关处理得到相位延迟的估计值,充分利用了各阵元间下行信号的相关性,合成效率较高。但正是这一特点,Sumple算法合成信号的相位中心收敛于一种随机状态,即合成信号不具备固定的相位中心特性,无法进行干涉测量处理。
结合Sumple算法信号合成特点,若各阵元信号的初始相位是一致的,那么流转的“参考信号”相位与各阵元信号的相位也是一致的,合成信号的相位与所有阵元信号的相位也一致,从而使合成信号具有固定的相位中心特性。鉴于此,提出了一种基于相位补偿的Sumple改进算法(RSumple算法),算法框图如图 2所示。
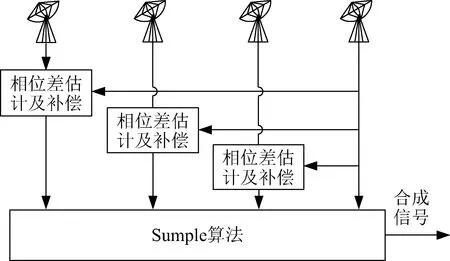
图2 基于相位补偿的Sumple算法框图Fig.2 The Sumple algorithm based on phase compensation
该算法首先选择参考阵元(通常选择G/T值最大的阵元),通过高精度相位估计得到其余阵元信号相对参考信号的相位差,然后以此对其余阵元下行信号进行相位补偿,使所有天线接收信号相位与参考信号一致;最后采用Sumple算法对所有阵元信号进行合成。
为进一步说明不同算法合成信号的相位特性,图 3给出了Simple算法、Sumple算法和RSumple算法合成信号与理想参考信号的时域波形对比,可以看出Simple算法和RSumple算法的合成信号与理想参考信号基本重合,即两种算法的合成信号具有固定的、稳定的相位特性。

图3 不同算法合成信号与参考信号时域波形对比Fig.3 The time-domain waveform comparison between reference and combined signals
本文所提RSumple算法合成过程本质上与Sumple算法相同,区别在于各阵元信号合成前需要进行相位补偿,因此该算法的浮点运算量为(N-1)·L+N·L·I。其中N为天线个数,L为每次迭代的相关长度,I为迭代次数,(N-1)·L为N-1个阵元相对参考阵元进行相位补偿引入的计算量[7]。
1.3 无线电干涉测量信号合成方法
RSumple算法解决了多个测站单一信号(如探测器下行信号中某个DOR信标)的合成问题,但在干涉测量中需要多个DOR信标同时相关处理才能实现高精度时延/时延率估计[12]。若要实现含有多个DOR信标的信号合成,则要求所有DOR信标信号同时在相位上对齐,那么时延估计精度必须达到亚纳秒量级(根据CCSDS标准,X频段设置两组DOR信标,频率跨度约40 MHz,信号合成所需时延补偿精度约为0.25 ns[13])。但是,干涉测量时延估计精度达到亚纳秒量级,已经满足深空探测任务需求,通过天线组阵改善测量精度意义不大;另一方面,目前基于DOR信号的时延估计精度很难达到亚纳秒量级,直接进行多通道信号合成存在较大的技术难度。以上两个方面使天线组阵在干涉测量中的应用面临两难境地。
考虑到目前深空探测数据一般采用多通道采集模式,每个通道采集一个DOR信标信号(一个通道含有多个DOR信标时,可分别处理),每个通道的DOR信号均可建模为正弦信号,而正弦信号不存在波前概念,因此可对各DOR信号分别合成处理,再对每个DOR合成信号进行相关处理,实现干涉测量,如图 4所示。

图4 信号合成干涉测量处理示意Fig.4 The data processing scheme of interferometry based on signal combination
假设干涉测量系统有A、B两个测站,其中A有一个深空探测天线(即阵元),B站(B1、B2、……、BN)有N个阵元;两个DOR信号频率为f1、f2,φA1、φA2、φBn_1、φBn_2分别为A站天线和B站第n(1≤n≤N)个阵元两个DOR信号的相位,则以A站和B站第n个阵元组成基线的时延估计为:

(10)
对B站所有阵元接收信号的两个DOR信号分别按照图 2所示的方法进行处理。不失一般性,假设B站以第1个阵元为参考,通过相位差估计求得B站第n个阵元相对第1个阵元的差分相位:
ΔφBn1_i=ΔφBn_i-ΔφB1_i,2≤n≤N
(11)
式中:i=1、2,表示两个DOR信号。以式(11)中所得的相位差对B站第n个阵元第i个DOR信号进行补偿。假设采样频率为fs,则补偿前后DOR信号可如下式所示,其中k为采样点序号。
Sn_i=sin(2πkfi/fs+φBn_i)

(12)
对B站第i个DOR信号的所有补偿信号利用Sumple算法进行合成,得到合成信号SBCi,其中,i=1、2,表示两个DOR信号。最后将合成信号与A站信号进行相关处理,得到时延估计:
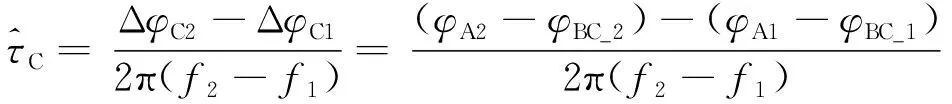
(13)
2 仿真与试验验证分析
2.1 信号合成算法仿真分析
假设测站阵元数为10,信号模型为正弦信号,采样率为1 MHz,信号频率为50 kHz,蒙特卡洛仿真次数为200。图 5给出了不同合成算法的性能对比。由图 5(a)可以看出,RSumple算法的合成性能优于Sumple算法及Simple算法;当参考阵元信噪比较高时,三种算法的合成效率均优于90%。
由图 5(b)上图可以看出,参考信号(Reference)、Simple算法合成信号(Simple)和RSumple算法合成信号的相位估计偏差均在0附近(Sumple算法相位估计偏差太大而无法同时清晰显示),说明三个信号的相位与理想参考信号保持一致;由图 5(b)下图可以看出,RSumple算法的相位估计性能明显优于参考信号和Simple算法。图 5的结果表明,改进算法通过相位补偿保证合成信号与参考信号的相位一致性,然后以补偿信号进行Sumple算法合成,相对Simple算法明显提高了合成性能,且合成信号的相位与参考信号保持一致。


图5 不同合成算法性能对比Fig.5 The performance comparison of different algorithms
2.2 信号合成算法试验数据验证
相控阵天线同时产生多个波束(试验系统的相控阵天线为5个波束),每个波束等效于一个天线,将不同波束的接收信号进行合成处理,改善接收信号质量。验证方案如图6所示。

图6 基于相控阵天线的组阵数据处理验证方案Fig.6 The verification scheme based on phased-array antenna
以某次试验的单频信标信号(信号频率为2 201.501 2 MHz)处理进行验证。信号的频谱如图 7所示,其中波束1~5的信噪比分别为16.974 8 dBHz、15.816 0 dBHz、16.990 7 dBHz、16.964 2 dBHz、16.997 9 dBHz。

图7 相控阵天线5个波束信号频谱Fig.7 The spectrum of phased-array data
相位估计结果表明,图7中波束1~5的相位估计随机精度分别为0.017 599 rad、0.020 076 rad、0.018 714 rad、0.015 977 rad、0.017 274 rad。选择波束5的接收信号为参考,进行信号合成。首先估计不同波束信号的相位差,图8给出了其余波束相对波束5的信号差分相位。

图8 不同波束间初始差分相位(以波束5为参考)Fig.8 The initial phase difference between beams (beam 5 as reference)
由图8可以看出,各波束信号相对参考信号的差分相位基本稳定,经统计波束1、2、4、5的接收信号相对参考信号的差分相位均值分别为 -1.999 114 rad、1.815 179 rad、 -1.748 355 rad、-2.280 054 rad。
然后,以上述差分相位均值对各个波束的接收信号进行补偿,补偿后各波束信号相对参考信号的差分相位如图9所示。

图9 相位补偿后各波束信号相对参考信号的差分相位Fig.9 The phase difference between beams after phase compensation (beam 5 as reference)
图9中差分相位均值分别为-0.444 1×10-15rad、-0.846 5×10-15rad、0.867 4×10-15rad、0.464 9×10-15rad,几乎为零。选择信噪比相对高的1、2、3、4波束进行信号合成,权值分别为0.9947、0.9983、0.9923和1.0000。此时,合成信号的信噪比为22.970 8 dBHz,理论合成信噪比为22.986 6 dBHz,信噪比合成效率为99.64%;合成信号的相位随机误差为0.009 469 rad,相对波束5的初始相位随机误差改善了约45.18%,由式(3)可得相位随机精度改善预期为50%,两者基本相符。
2.3 基于信号合成的无线电干涉测量仿真
假设干涉测量系统有A、B两个测站,其中A有一个深空探测天线(即阵元),B站(B1、B2、B3、B4)有4个深空探测天线;航天器下行信号含有两组DOR音,相距载波频率分别为3.85 MHz和19.2 MHz;信号采样率为128 MHz,载波频率为24 MHz;航天器相对A-B1基线、A-B2基线、A-B3基线、A-B4基线的真实时延差分别为5Ts、6Ts、7Ts、4Ts(Ts为采样周期);蒙特卡罗仿真次数500。将B站4个天线接收信号进行合成,然后与A站信号进行相关处理。时延估计结果如图 10所示,其中Original表示A-B1基线时延估计性能。可以看出,合成信号相关处理得到的时延估计偏差抖动更小;时延估计随机精度相对提高,最大改善约51.5%,最小改善12.4%,平均改善幅度25.8%。利用式(9)计算(M=1,N=4,η=95%),理论预期改善幅度约为20%,两者基本相符。

图10 基于信号合成的时延估计性能Fig.10 Delay estimation performance based on signal combination
3 结束语
本文在后续深空探测任务测量精度要求更高的背景下,提出了利用信号合成改善无线电干涉测量精度的方案,并理论分析了信号合成对相位估计性能和时延估计性能的改善;结合无线电干涉测量对合成信号相位特性的要求,提出了基于相位补偿的Sumple算法,该算法不仅合成效率高,且合成信号具有与参考相同的相位特性,满足无线电干涉测量要求;利用相控阵试验数据和仿真数据对合成方案和合成算法进行了验证,结果表明,信号合成处理可以提高无线电干涉测量精度。这在后续深空探测任务中具有重要意义。

