高灵敏光纤光栅加速度检波器理论模型研究

刘钦朋，何 雪，贾振安，傅海威，高 宏，禹大宽

(西安石油大学 理学院 陕西省油气资源光纤探测工程技术研究中心陕西省油气井测控技术重点实验室，陕西 西安710065)

引言

随着光纤光栅技术的日渐发展，基于光纤光栅的传感器件层出不穷，其中光纤布拉格光栅(fiber Bragg grating,FBG)应用最为广泛，在准静态领域取得了长足的发展，各种不同类型的准静态FBG传感器逐渐应用于不同的工程领域。随着FBG应用技术的不断拓展，FBG动态传感技术引起研究者的广泛关注。自T.A.Berkoff[1]在1996年首次将光纤光栅运用于振动信号测量之后，光纤光栅在加速度检波技术方面的应用便引起了学者们的广泛关注。近年来，FBG加速度传感技术取得了迅猛的发展，并在诸多行业领域具有潜在的应用价值，如结构健康监测、油气勘探开采[2-8]等。加速度检波器的核心技术是设计不同结构的惯性系统，结合FBG的尺度特点和传感机理，通过两点封装方式或全粘方式，实现高灵敏、宽频带、低交叉干扰的关键技术参数。针对FBG检波技术的研究热点主要集中在检波器的结构设计、封装技术和FBG动态解调技术，其中FBG检波器是整个系统最前端的器件，直接决定动态信号的拾取成败，所以检波器是整个系统的关键器件。

根据检波器的弹性结构，FBG检波器可分为悬臂梁结构[9-17]、弹性柱体式结构[18-23]、弹性膜片结构[24-26]、特殊弹性体结构[27-28]等。基于单悬臂梁结构的FBG检波器结构简单容易实现，研究的热点主要集于提高传感器灵敏度，封装方式主要基于全粘封装，但容易导致光栅啁啾，同时该结构的横向抗干扰是一个难于解决的问题。为了增强横向抗干扰，研究者们提出多梁结构FBG检波器[16-17]。相对悬臂梁结构，弹性柱体结构FBG检波器的轴向刚度容易控制，有利于设计不同频段的加速度检波器，但横向干扰难以降低。Yu等[18]提出了一种柱体FBG加速度传感器，灵敏度达80 pm/G，谐振频率为388 Hz，刘钦朋等[19]提出了一种弹性管式FBG加速度传感器，灵敏度为63 pm/G，谐振频率为376 Hz，Wang等[20]提出了一种小型化FBG加速度传感器，灵敏度为54 pm/G，谐振频率为480 Hz，Zhang等[21]提出了一种顺变柱体FBG加速度传感器，灵敏度为42.7 pm/G，谐振频率为400 Hz，Gutiérrea等[22]提出了一种柱体结构FBG加速度检波器，灵敏度为19.6 pm/G，谐振频率为500 Hz，Guo等[23]提出了一种高频加速度传感器，灵敏度约为4 pm/G，谐振频率为3 806 Hz。弹性膜片结构具有法相位移敏感横向位移不敏感的特性，非常适合加速度检波器的设计。Muller等[24]提出了基于膜片结构的理论思想。Liu等[25]提出了一种单膜片环向封装的FBG加速度检波器，灵敏度约为36.6 pm/G，谐振频率为255 Hz，交叉灵敏度小于1.3%，在此基础上，提出了双膜片FBG的加速度检波器[26]，灵敏度约为23.8 pm/G，谐振频率为1240 Hz，交叉灵敏度小于2.1%。

根据惯性系统的基本理论可得加速度检波器的谐振频率与加速度灵敏度之间是反比关系，如何优化参数，加速度灵敏度和谐振频率满足什么样的制约关系，弄清这些问题是设计高性能加速度检波器的前提。论文首先建立两点封装FBG加速检波器的一般模型，推导灵敏度解析表达式，理论分析加速度灵敏度的影响因素，讨论加速度灵敏度与谐振频率的制约关系，引入品质因数，为检波器综合性能的优化和判定奠定基础，对FBG加速度检波器的设计具有重要的指导意义。

1 高灵敏FBG加速度检波器理论模型

1.1 FBG传感原理

FBG是在二氧化硅光纤纤芯内使用紫外光垂直照射相位掩模板从而形成的折射率周期调制的全光纤无源器件。其反射波的中心波长满足布拉格定律，中心波长可由(1)式给出[1]

λB=2neffΛ

(1)

式中:λB为反射波的中心波长;neff为光纤纤芯的有效折射率;Λ为光栅的调制周期。光纤光栅上应变或者外界环境温度变化会导致光纤光栅的neff和Λ发生变化，当应变变化量和温度变化量分别为Δε、ΔT时，FBG中心波长的相对漂移量可表示为[1]

(2)

式中:Δε为光纤的有效弹性系数;Δε为光纤光栅的轴向应变量;αf为光纤的热膨胀系数;ζ为光纤的热光系数。光纤光栅会同时对温度和应变产生响应，当忽略温度变化影响，只考虑受光纤光栅上应变变化带来的中心波长改变那么(2)式可简化为(3)式，对于一般掺锗二氧化硅光纤有Pe≈0.22。

(3)

1.2 FBG加速度检波器理论模型

加速度检波器是根据惯性原理所设计，惯性式FBG加速度检波器力学模型如图1所示，其通过底座进行固定，为典型的FBG加速度检波器力学模型“弹簧-阻尼-质量”系统。FBG加速度检波器是由惯性质量块、弹性器件及阻尼构成，FBG加速度检波器可看成一个单自由度二阶振动系统。当加入外界振动信号激励时，质量块在惯性作用下将产生位移，在阻尼和弹性器件的共同作用下外界振动信号通过结构作用到FBG上导致光纤轴向伸缩，引起FBG的轴向应变，最终实现光栅波长调制，从而实现加速度的测量。

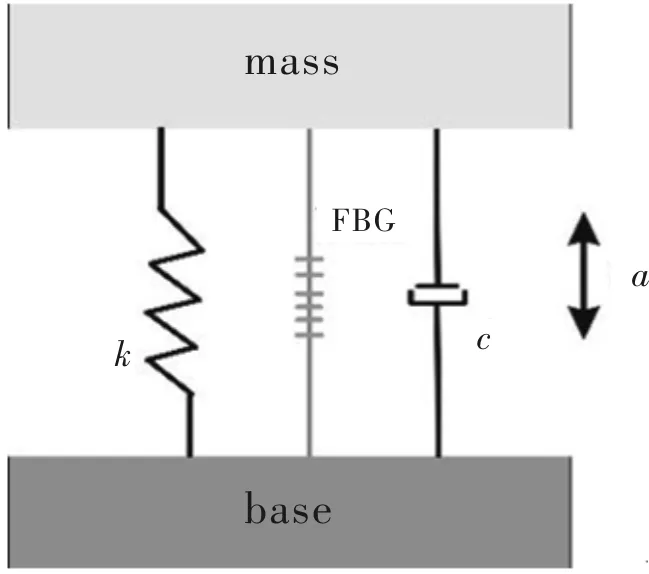
图1 加速度检波器一般力学模型Fig.1 Common mechanical model of acceleration detector

当FBG加速度检波器受到外界激励信号时，若只考虑应变对光纤光栅带来的影响时，惯性质量块受到的惯性力F=ma恰好与运动方向相反，此时检波器中已经封装好的FBG有效折射率和周期会发生改变，FBG的中心波长将会随之发生变化且满足(3)式。FBG检波器拾取到外界的振动信号，经传输光纤从环境传到光纤光栅动态解调仪从而得到FBG中心波长的变化量，再经过数据处理得到中心波长变化量和外界激励信号加速度之间的比值，即得到该检波器对外界振动信号加速度的灵敏度，从而精确地反映出外界振动信号的各项参数。

惯性质量块相对于参考空间坐标原点的位移为x(t)，检波器外壳相对于参考空间坐标原点产生的位移为y(t)，那么质量块与检波器外壳的相对位移为A(t)=x(t)-y(t)，根据牛顿运动定律，以惯性质量块作为研究对象，可得方程：

(4)

式中：m为惯性质量块的质量;c为系统的阻尼;Keff为弹性系统有效刚度系数。将质量块与检波器外壳的相对位移A(t)引入(4)式，整理可得：

(5)

假设加速度检波器在理想的竖直方向进行振动，由于所施加外界激励信号为连续的，因此检波器所受到的激励也为连续，任何信号都可以由不同频率正弦波叠加得到，可假设y(t)=F0sinωt，其中F0为激励信号的幅值，ω为激励信号的角频率，则可得到检波器在受外界信号激励作用下的运动方程：

(6)

(7)

(8)

由(8)式可得惯性质量块与检波器外壳之间相对位移量A(t)与外界激励信号的加速度值有关，此外，外界加速度激励信号将会改变振幅，导致封装光纤长度改变，产生应变，造成FBG波长的漂移。当封装光纤的长度为L时，FBG的轴向应变可被表示为

(9)

将(8)式和(9)式带入(3)式整理得：

(10)

综合(10)式，当外界激励信号频率远小于检波器自身谐振频率时，ω/ω0≪1；且检波器为欠阻尼状态，因此FBG中心波长对加速度的响应灵敏度S为

(11)

(11)式中的灵敏度称为静态灵敏度，引入Ks为检波器结构部分刚度系数，Kf为所封装光纤刚度系数。已知光纤的杨氏模量Ef=7.3×1010Pa及直径df=125 μm，当封装光纤光栅长度L确定时，即可由Kf=EfB/L,其中B为光纤横截面面积，得到对应光纤的刚度系数。定义η=Ks/Kf，当Kf为已知量时，则可将检波器系统有效刚度系数用Kf表征：

(12)

当研究对象为具体器件时，需要考虑的参数包括结构参数、封装光纤的参数，其中结构参数主要影响器件的刚度系数和等效惯性质量，(12)式中M即为实际设计中器件的等效质量。封装光纤的参数主要影响光纤的刚度，进而影响系统的刚度。由(12)式可得出检波器的加速度灵敏度和检波器装置的等效质量、有效刚度系数和封装光纤长度有关，因此可根据不同频段的应用需求，改变装置的选材和尺寸(弹性模量、刚度系数和密度)来改变器件的等效质量和谐振频率,从而达到提高灵敏度的目的。

从有效刚度系数为分析点出发，以检波器结构和封装光纤之间的刚度比值为切入点对加速度的灵敏度进行深入讨论，理论分析刚度比值η不同时其对检波器的谐振频率、灵敏度的影响。根据η=Ks/Kf，则检波器系统的谐振频率可表示为

2 加速度灵敏度、谐振频率及品质因数

速度检波器的两个最主要的技术参数加速度灵敏度S和谐振频率fn是相互制约的关系，提高灵敏度必然伴随谐振频率的降低，反之亦然。在给定频带内，如何提高灵敏度，是优化的一个重要目标，在给定频带内，灵敏度的分布与结构参数及封装光纤的关系是优化的前提，由此，我们引入优化理论依据——谐振频率与灵敏度之积作为品质因数，能够为不同结构的FBG加速度传感器的综合性能比较提供了可能，而不是片面的只追求高的加速度灵敏度或低谐振频率，能比较客观评价加速度传感器的综合性能。根据理论灵敏度和谐振频率的表达式，结合结构参数(如表1)，便可反映灵敏度与谐振频率的关系。如图2所示，描述了质量与封装光纤长度对灵敏度和谐振频率的影响。

表1 检波器结构参数

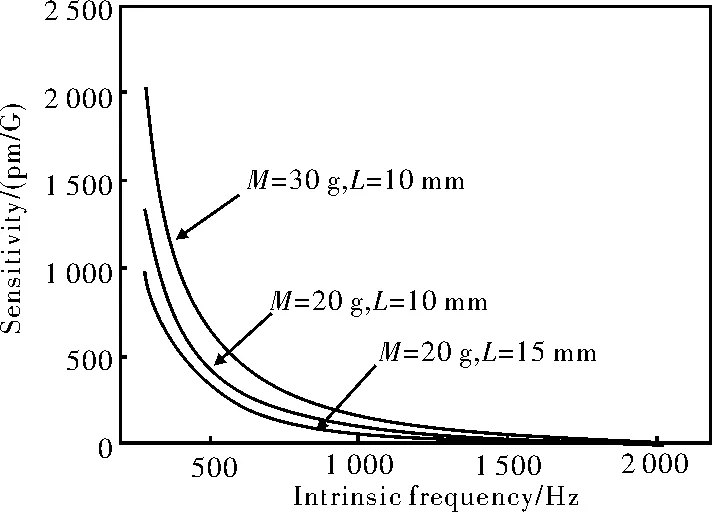
图2 谐振频率和灵敏度之间一般关系曲线Fig. 2 General relationship curve between resonant frequency and sensitivity

在实际应用中，如何在固定频带内提高灵敏度是一个非常有意义的问题。同时，检波器在固定频带内极限灵敏度的分布特征对检波器的设计也具有极其重要的指导意义。因此，需对加速度灵敏度S和谐振频率fn之间的量化制约关系进行分析,研究极限灵敏度的分布及频率分布的关系。并根据灵敏度和谐振频率之间的制约关系，定义FBG检波器加速度灵敏度与谐振频率之积为品质因数，记作Q，不仅能为提高灵敏度提供参数优化方案而且可用于评价检波器的综合性能。

Q=S·fn

(14)

式中S、fn分别为检波器对外界加速度的灵敏度和谐振频率。由(14)式可知品质因数是由灵敏度和谐振频率共同决定的。因此，当要对检波器技术参数进行综合考量时可以选择品质因数较大的，这更符合加速度检波器结构参数优化的需求。高灵敏是设计者追求的目标，希望不仅可以提高信号的分辨率，同时还可以改善低频段信号响应特性。针对图1的检波器理论模型，并结合(12)式、(13)式和(14)式，该关系式可通用于所有两点封装结构的FBG加速度检波器模型。

刚度比值η会影响器件的响应特性。随着等效质量的增大，η不同时(参数见表2)，不同的刚度比值η对于谐振频率fn和加速度灵敏度的影响如图3(a)所示，当等效质量一定时，η越小的灵敏度相对较大，反之则否。不同的加速度检波器有不同的工作频率范围，但无论是什么工作频率范围，都更希望它的工作灵敏度能够相对而言的更高。可以发现，η较大的器件可在等效质量较小情况下在宽频带实现高灵敏度；反之，若想用于较低频率信号的探测则需要更大的等效质量。图3(b)为响应情况下品质因数Q的曲线变化，可明显看出当封装光纤长度和等效质量一定时，η较小的，其Q值更大。

表2 加速度检波器结构参数取值

图3 (a)η不同时谐振频率和灵敏度曲线;(b)η不同时随着质量的增加品质因数Q曲线Fig.3 (a) Curve of fn and with different η; (b)Curve of Q with different ηas M increases

刚度比值会影响器件的响应特性。随着比值 的增大，等效质量不同的情况时(参数见表3)，谐振频率fn和灵敏度S的曲线变化如图4(a)、(c)所示，当η一定时，等效质量越大，对应的灵敏度较大，而谐振频率较小；反之，等效质量较小时，对应的谐振频率却较大，对应的灵敏度较小。图4(b)、(d)为相应情况下品质因数Q的变化曲线。从图中可以很明显地看出当封装光纤长度和刚度比值一定时，等效质量越大时，Q值相对较大。此外，特别分析了当刚度比值η∈[0,1]时的情况，是为检波器结构刚度远小于光纤刚度。虽然该情况在一般的FBG加速度检波器装置中较难实现，但是从图4(c)、(d)曲线变化中不难看出其符合文中所提出的一般加速度检波器模型条件。

表3 加速度检波器结构参数取值

图4 (a)不同质量下谐振频率和灵敏度曲线;(b)不同质量下品质因数Q曲线(η∈[0,100]);(c) 不同质量下谐振频率和灵敏度曲线; (d) 不同质量下品质因数Q曲线(η∈[0,1])Fig.4 (a) Relationship between fn and S with different M; (b)Curve of Q with different M (η∈[0,100] );(c)Relationship between fn and S with different M; (d)Curve of Q with different M (η∈[0,1])

当检波器系统结构和光纤之间刚度比值η一定，封装光纤长度不同时(参数见表4)。随着等效质量的增大，谐振频率和灵敏度的关系变化曲线如图5(a)所示，不同长度的封装光纤其灵敏度曲线却重合，根据(12)式，并结合光纤刚度表达式Kf=EfB/L可得到公式(15)，即从刚度比值出发考虑检波器灵敏度时，拥有不同长度的封装光纤的检波器可能会具有相同的加速度灵敏度，也从侧面证明利用品质因数来进行综合考虑检波器性能的必要性，可为检波器器件的高灵敏度提供参数优化方案。

(15)

表4 加速度检波器结构参数取值

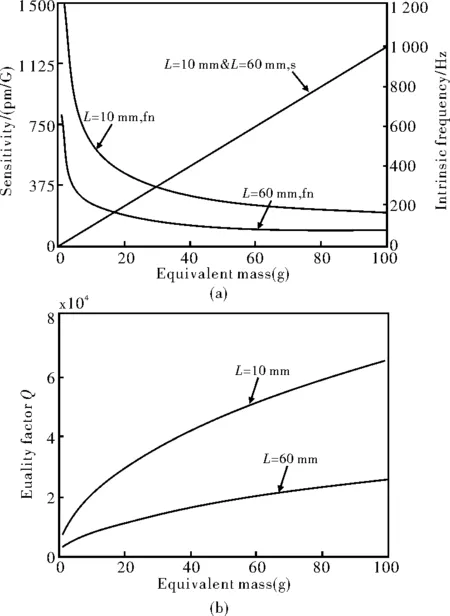
图5 (a)η值不同时系统谐振频率和灵敏度曲线;(b)η值不同时品质因数Q曲线Fig. 5 (a)Relationship between fn and with different η;(b) Curve of Q with different η

另一方面，随着等效质量的增大，系统谐振频率都逐渐减小，但是当等效质量一定时，封装光纤长度较长的检波器所对应的谐振频率更小。图5(b)为相应情况下的品质因数Q的变化曲线，综合品质因数Q进行考虑时，当刚度比值η和检波器等效质量一定时，选择封装光纤长度较短的器件明显综合性能更好且更容易实现高灵敏度。

从以上各图可看出在低频段，刚度比值η对灵敏度的影响起主要作用，特别是在超低频段尤为明显；而在高频段(>500 Hz)由于结构刚度远大于光纤刚度，封装光纤的刚度对器件整体刚度的贡献越来越少，因此对灵敏度和谐振频率的影响也逐渐减小。其次，可发现当封装光纤长度和等效质量不同时，不同检波器仍可能具有相近的灵敏度或谐振频率，即不同的检波器结构参数可以实现同样灵敏度或频带分布，此时会很难对这些检波器的综合性能进行评定，这也是为什么要引入品质因数Q的重要原因。

总得来说，当以η值和已知光纤刚度系数来给定一个加速度检波器的有效刚度系数时，器件整体刚度受封装光纤长度、器件等效质量的共同影响，但不同封装光纤长度的器件却可能获得相同的加速度灵敏度。器件等效质量可通过改变其材料或调节尺寸大小进行改变，但刚度比值η不再是一个量化的数字，这时候需要综合考虑所设计检波器的工作频率范围和结构大小并根据理论需要弹性模量来选择适合结构所用材料。

3 结论

结合加速度检波器一般力学模型及FBG传感理论，综合分析了等效质量、刚度比值及封装光纤长度在不同参数范围下检波器的响应，讨论了参数变化对系统谐振频率和加速度灵敏度的影响；并引入了品质因数Q，可在全面考虑器件性能情况下同时提供高灵敏度和宽工作频带的优化方案。综合考虑参数变化对检波器响应特性的影响，且通过品质因数Q能够更好地评价检波器的综合性能和优化器件性能。提出的理论模型对加速度检波器的优化设计具有重要的理论指导依据，为研制出满足技术参数的高灵敏度加速度检波器奠定了一定的理论基础。