基于累积梯度的裂缝提取算法

魏永杰，葛婷婷，张中岐，马宝强，车进超

(河北工业大学 机械工程学院，天津 300130)

引言

建筑物的破坏往往是从裂缝开始的，各种原因产生的裂缝影响结构的正常使用、耐久性和安全性。对裂缝进行长期的监测可以及时掌握建筑物裂缝变化的情况和规律，为建筑物的质量检测提供依据。基于图像法的裂缝检测方法在该领域得到了广泛应用[1]。

裂缝的图像检测方法是典型的边界提取算法。为了从图像中提取边缘，通常会使用到边缘检测算子[2]，如Sobel算子、prewitt算子、log算子、Roberts算子和Laplacian算子等。其中Sobel算子并没有将图像的主题与背景严格地区分开来，没有基于图像灰度进行处理，所以提取的图像轮廓有时并不能令人满意；在现场测量距离远、镜头焦距长的情况下，裂缝所处环境比较复杂，背景和光照信息多样，实际场景的图像包含的数据是不连续和模糊的，常用边缘检测方法对图像的复杂程度估计不够，难以满足工程应用的需求，结果往往不能令人满意。因此，研究如何消除噪声的边缘提取算法是目前的一个热点问题。

目前，在常用的裂缝检测算法中[3]，最为著名的是Otsu算法，它能够应用于多种边缘检测算子，可有效降低噪声的影响[4]。HA算法是较早提出的一种方法，有效地解决了裂缝节点识别困难、缺陷处理量小等常规方法不能解决的问题[5]。采用基于小波变换的裂缝检测方法，可将图像变换到不同方向的子带进行裂缝提取[6]。将形态学方法用于裂缝检测，可通过中值滤波、灰度形态算子等边缘检测算法检测具有较高对比度的裂缝[7]。考虑到光照等周围环境对图像造成的剧烈影响，有人提出了基于自适应模糊的局部区域图像增强算法[8]。此外，由于二维影像平面处理，没有充分考虑裂缝所处的物方三维空间，很难建立精确的数学模型，导致计算的裂缝尺寸具有较大的误差[9]，因此有人将二维图像转化到三维空间进行测量[10]，除对平面图像进行处理外，用双目立体视觉模型测量裂缝的空间尺寸，弥补了二维建模和测量精度的缺陷[11]，但在光线条件较差时容易导致匹配和计算精度下降[12]。

常用常规图像法提取裂缝，识别位置和尺寸信息比较困难。因此，基于图像形态学的基本原理，提出累积梯度算法，用于裂缝的图像识别。

1 原理

对于建筑物的各种裂缝，在有光照情况下表现为暗线条，以灰度图像表示，为较小的灰度值。如果背景为均匀且噪声小的高灰度值，则可通过设定域值，将图像直接转化为二值化图像，得到裂缝信息。而在多数情况下，裂缝所处背景复杂，尤其是在建筑物上，由于材料及建造工艺等因素影响，使得根本无法得到裂缝缺陷信息。图1是采集到的含有裂缝的建筑物原始图片及处理结果。其中图1(a)是原始图片，该雕塑上面有一条清晰裂缝。图1(b)是经直方图均衡化的结果，可见该图片光照不均均，左侧光强，右侧光弱，但即便是在右侧光照非常差的范围内，人眼也能够观察到裂缝。图中花岗岩的纹理非常明显，且有许多斑点，这些对检测结果都会产生影响。图2是采用Otsu算法处理的结果。该结果不能提取到所有的裂缝区域。

图1 含有裂缝的图像Fig.1 Image with crack

图2 Otsu算法处理结果Fig.2 Result with Otsu

图3是分别采用6种边缘检测算子检测的结果。图3中所采用的边缘检测算子对于标准图像均可得到较好效果，但对于图1的实验照片只可见到一条模糊边界，如图3(a)、(b)所示，这条裂缝在右侧暗区是观察不到的，且这些算子得到的图像含有大量孤立噪声点。对比图1(b)，图3中的6幅图像右侧均为零值，与图1中光照较差有关。由图3结果可见，这些算子均不能满足图1的检测要求。

图3 常用边缘算子检测结果Fig.3 Results by commonly used edge detection operators

为解决上述问题，在对原始图像滤波的基础上，首先采用自适应二值化方法得到裂缝的边缘信息[13]。该算法是基于每个像素点选取不同的域值来达到二值化目的。它是通过计算像素点周围的一个小区域内进行加权平均，然后减去一个常数来得到自适应阈值[14]。即:

(1)

式中：Ti表示第i个像素点的域值；Gmn表示第i点周围[-b,b]×[-b,b]的区域内各点的像素值。(1)式中右侧第一项表示加权平均，可采用平均加权方法或高斯加权方法。C为选定的常数，该参数根据图像对比度及光照均匀程度选取。本文的裂缝为低灰度值，应选择较小的C值，得到处理后的裂缝比实际裂缝宽，以便于后续处理。

在(1)式处理后的二值化图像中可观察到明显的裂缝形状，但该图像仍含有大量噪声，不能满足计算机处理的要求。为此，基于计算机图像形态学和OpenCV计算机视觉库[15]，对结果进行进一步处理。

二值化后裂缝的灰度值为0，通过图像形态学的腐蚀操作可将(1)式处理的二值化图像孤立点连在一起，同时会将灰度值为0的噪声点范围扩大，采用比腐蚀窗口稍大的窗口进行一次闭操作可消除噪声点。

为了进行裂缝识别，需要对形态学操作后进行去噪声、识别和提取。因此，可采用连通域方法，将裂缝和噪声分别连接为连通区域，并找到这些连通区域的边界。

裂缝特征和噪声具有不同的连通域特征。裂缝一般为极窄极长的连通域，噪声区域为长宽比相差不多的连通域且面积较小，考虑几何图形周长和面积的关系，可去掉二值化图像中大部分噪声信号。设裂缝宽度为b且相差不多，长度为a，周长为l，面积为S，长宽比a∶b=m，则面积和周长的比值k为

(2)

由(2)式可知，对于宽度为定值的裂缝，如果设定长宽比为m0，则可得到面积和周长平方的比值k0。根据裂缝的特性，一般长度要比宽度大很多。设a∶b>m0时为裂缝，则k>k0，反之为噪声。通过连通域计算，可得到各个连通域的面积S和长度l。根据上述判据，可将a∶b≤m0的连通域作为噪声去除。同时，当面积S很小时，对于我们研究裂缝无意义，因此将a∶b>m0且面积很小的连通域也作为噪声区域去除，得到裂缝连通域。对于少数噪声点也可手动删除。

经过自适应二值化和图像形态学操作后的裂缝连通域与原始图像的裂缝形状相同但范围扩大，即裂缝变宽，不能满足测量需要。为解决上述问题，提出了累积梯度算法。

所谓累积梯度算法，即将二值化和图像形态学操作后的裂缝连通域作为掩模区域，该区域比裂缝区域宽，灰度值为零。对照掩模区域，将原始图像灰度值相加，得累积灰度值Gk。对该掩模区域进行膨胀操作，掩模区域变小，将对应的原始图像灰度值相加得Gk+1，设累积灰度差k为

(3)

式中：n、m分别为膨胀前后裂缝连通域模板的像素点数。对原始图像依次迭代膨胀；k为最大时即为累积梯度值，第k次膨胀前的原始图像即为识别出的裂缝图像。

2 实验

采用上述方法对图1(a)图像进行了处理，结果如图4所示。

其中图4(a)是对原始图像进行平均滤波后的结果，采用3×3的均值滤波窗口。图4(b)是自适应二值化的结果，图中采用31×31的窗口，考虑到裂缝为低灰度值，取常数C=4。由图4(b)可以明显看出裂缝区域，但周围噪声点很多，且裂缝不连续。图4(c)是采用7×7的窗口腐蚀后的结果，由于裂缝和噪声区域表现为低灰度值，与图4(b)相比，图4(c)的裂缝变宽，噪声区域也加大。为便于后续寻找连通域和噪声去除，采用更大些的窗口对图4(c)的腐蚀图像进行闭操作，如图4(d)所示，采用窗口为9×9。经闭操作后裂缝连通的区域没有被分割，但噪声区域变小。有利于寻找连通域边缘。图4(e)是找到并进行黑色内部填充的裂缝连通域，并根据周长及面积的关系式(2)将不符合裂缝特征的噪声区域删除后的结果。从图中可以看出，如果噪声与裂缝区域相连通，则该噪声区域不能自动删除，可采用手动方法进行删除。经手动删除后，可作为原始图像的掩模版图像，该图像为二值化图像，如图4(f)所示。

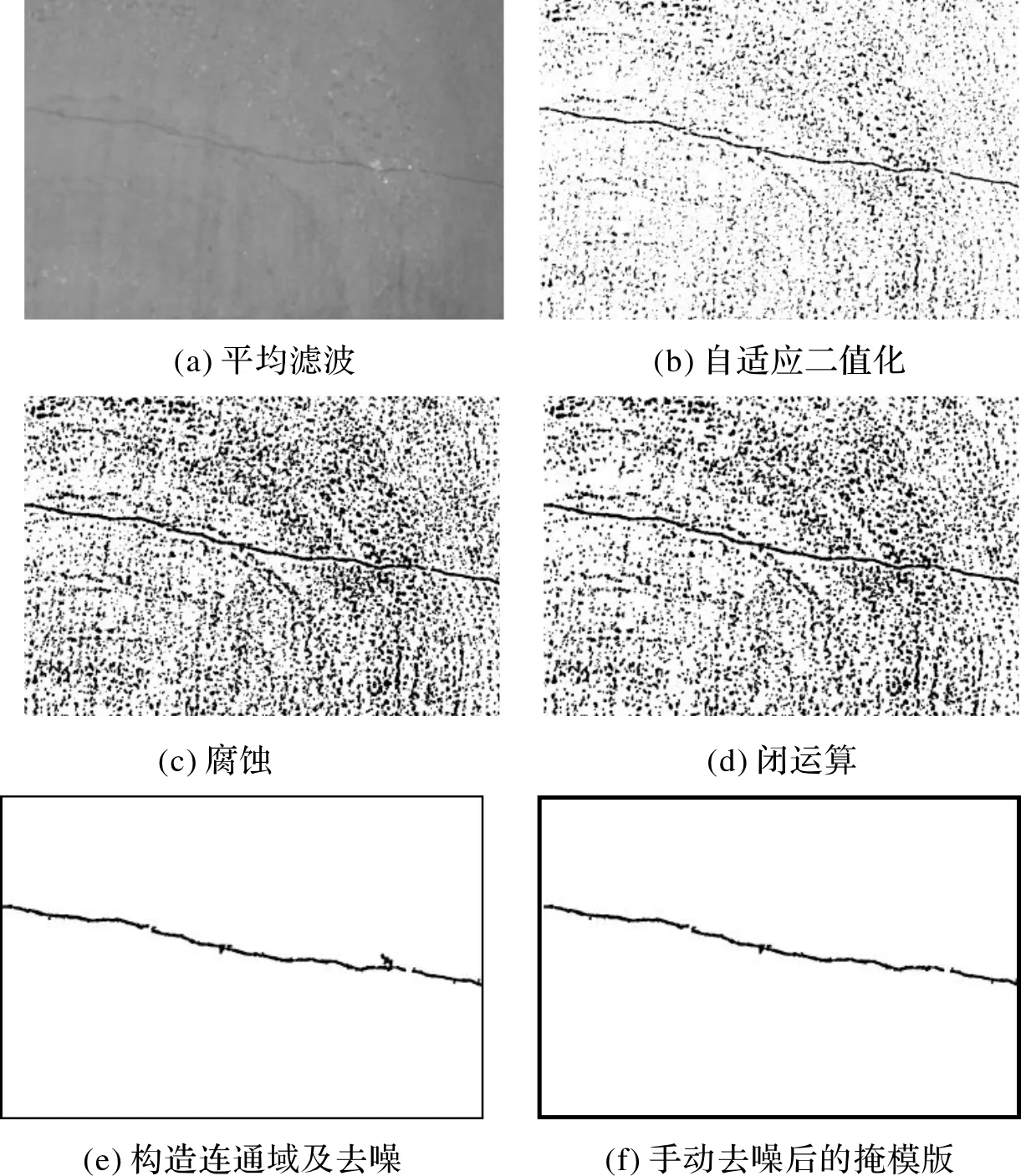
图4 累积梯度算法得到的模板Fig.4 Stencils by accumulated gradients

将图4(f)所示掩模版作用于原始图像，即在原始图像中只将对应掩模图像灰度值为零的部分进行膨胀操作，选取3×3的窗口进行迭代膨胀，原始图像中累积灰度变化k为最大值时，膨胀前结果为实际裂缝。图5为检测的最终结果。

图5 裂缝检测结果Fig.5 Crack result

图5中裂缝连通域为灰度图，背景以白色表示。图5与图4(b)～(e)相比，裂缝区域要窄，说明经自适应二值化和图像形态学操作后对于深色裂缝区域均会加宽。图6是采用图4(f)为模版，对原始图像进行迭代膨胀的灰度差变化曲线，在第7次膨胀时，该值达到最大，即为累积梯度，即第6次迭代膨胀后为图5的裂缝求解结果。

图6 迭代膨胀的灰度差变化曲线Fig.6 Gray difference in iterations

为验证该方法的有效性，对另外一种复杂背景条件下的样品进行了拍摄和处理。如图7所示。

图7 样品的拍摄和处理Fig.7 Sample shooting and processing

由图7(a)和7(b)的结果比较可以看出，采用该方法能够提取得到有裂缝区域。

3 结论

在自适应二值化和图像形态学的基础上，采用累积梯度算法，对裂缝连通域进行迭代膨胀运算，并计算膨胀前后的灰度差值。灰度差值最大时即为累积梯度，对应裂缝的边缘信息。采用上述方法可在背景复杂、光照不均的条件下提取得到裂缝信息，为建筑物的安全性检测提供预防手段。