一种基于混合分布模型的高分辨主动声呐目标检测方法

陈卓

（海装驻上海地区军事代表局，上海，200083）

在复杂多变的海洋环境中，海底礁石、水中鱼群、海面起伏等的声反射，引起了大量的主动声呐杂波；海底、海面的不平整性及水体的不均匀性等的声散射形成了主动声呐混响；航船噪声、风成噪声、降雨噪声、鱼虾噪声等引起了主动声呐噪声。当杂波、混响或噪声数据被误判为目标时，产生虚警，高虚警增加了人员辨别负担，而低虚警率则可能伴随着目标漏检。主动声呐系统中，一般采用恒定虚警率（Constant False Alarm Ratio, CFAR）进行设计。然而，高分辨主动声呐工作时（尤其是在浅海），其混响与杂波的统计特性严重偏离经典的瑞利分布，使得基于瑞利模型计算的检测门限在真实数据中呈现出远高于设计虚警率。

为解决非瑞利分布数据的目标恒定虚警率检测问题，需要更为准确地描述包含混响、杂波与噪声数据的分布特性。N P Chotiros、M Gensane等人分析了海底声散射的影响[1,2]，并对Rayleigh、Lognormal、Weibell、Mixture Rayleigh模型进行了对比研究；E Jakeman根据其长期的海面雷达杂波研究成果，经理论建模与数学推导，首次提出了K分布模型[3]，因其与实际数据的良好匹配性和清晰的物理意义而广泛应用于雷达目标检测。文献[4,5]将K分布引入到主动声呐探测杂波，分析了多种K分布的形状参数估计方法的性能，并验证了该模型的有效性。本文提出主动声呐的K-Gamma混合分布模型，将混合模型应用于目标检测门限设计，实现恒虚警检测。

1 Gamma分布和K分布

假设主动声呐波束域中的噪声数据幅值上满足瑞利分布，能量上服从指数分布。主动信号处理中，往往先对波束数据作平滑处理，改善了接收机的工作特性（Receiver Operating Characteristic,ROC）；其次，经二次均值（Two-Pass Mean，TPM）背景归一化处理[6]，TPM处理使得噪声数据的指数分布参数为1；最后，进行目标检测判别。噪声信号随机性较大，可假定噪声信号的邻近数据点满足相互独立条件，平滑处理使得指数分布转变为Gamma分布。杂波信号具有一定的信噪比，其数据点间存在一定的相干性，可假定杂波信号邻近数据点间相干，平滑处理后，仍为K分布。

1.1 Gamma分布

主动声呐信号处理中的平滑运算，统计意义上是多个独立同指数分布的求和平均，其结果服从Gamma分布。在波束域上，对N个连续的邻近数据xi（i=1,…,N）平滑处理表达式为

式中，N表示数据平滑的点数，一般N=8。

假设X1,X2…XN是独立同（指数）分布，则经平滑处理的累积分布函数（Cumulative Distribution Function, CDF）为

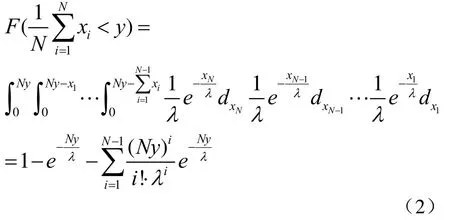
式中，λ为指数分布参数。

概率密度函数（Probability Density Function,PDF）则为

式中，Γ（⋅）表示Gamma函数。记Gamma分布的形状参数v=N，尺度参数则式（3）可写为

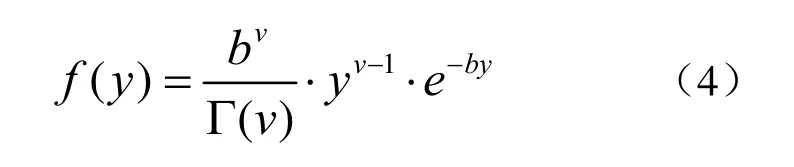
依据式（5），可通过形状参数计算尺度参数。

为直观显示不同平滑点数对概率分布函数的影响，平滑点数分别取为1、4、16，绘制Gamma分布的PDF，见图1。可以看出，随平滑点数的增加，Gamma分布越接近于高斯分布。

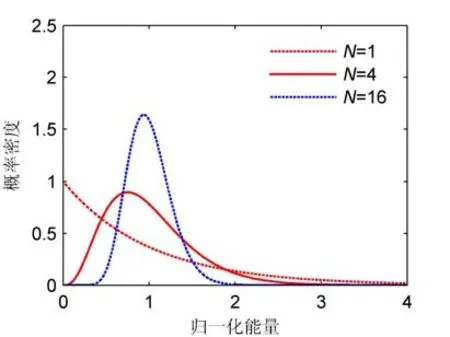
图1 N取不同值时Gamma分布的PDF

1.2 K分布

该模型基于局部性的起伏受平均效应调制，即局部强度z具有均值为y的指数分布，PDF为：

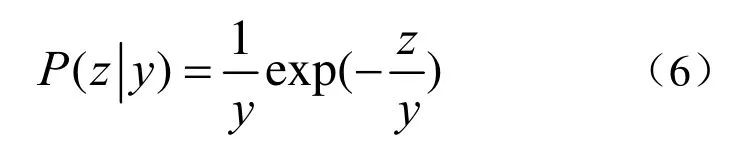
式中，y服从Gamma分布。那么

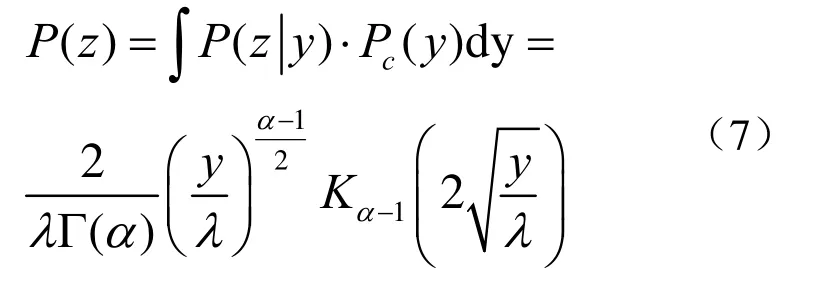
式中，Kα-1（⋅）为α-1阶变形第二类Bessel函数，α为决定K分布形状的形状参数。相应地，K分布的CDF为

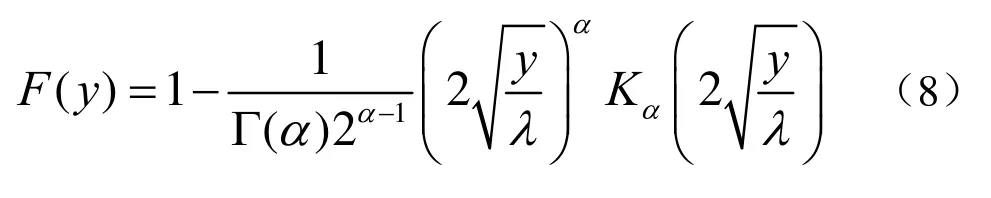
较大的水下散射体、脉冲信号模糊度、水声信道多途等使主动杂波信号中邻近数据点间存在一定的相干性，为分析简便，本文假设对杂波信号的平滑处理是相干信号叠加，仍满足K分布。同时，为直观显示不同形状参数对概率分布函数的影响，形状参数分别取0.5、1.0、4.0，绘制K分布的PDF曲线，如图2所示。可以看出，随K分布形状参数增大，其越接近指数分布。

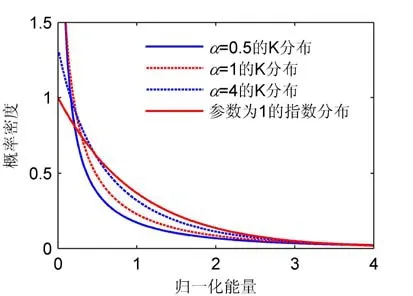
图2 不同形状参数时K分布的PDF

研究杂波幅度分布规律时，可利用式（9）和式（10），计算得到幅值数据的K分布PDF和CDF。

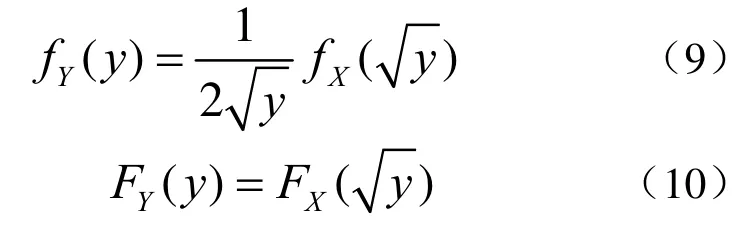
K分布的PDF为：

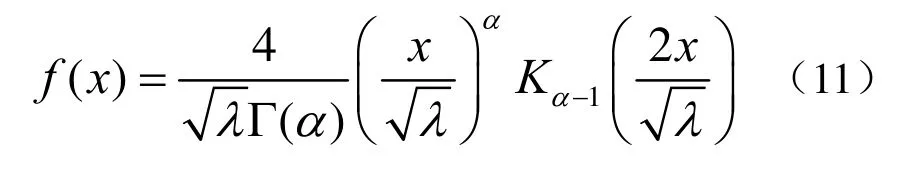
K分布的CDF为：

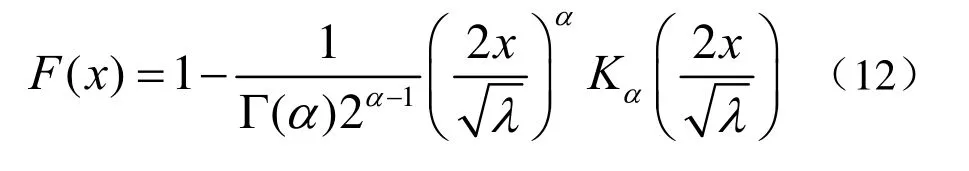
2 混合分布模型及模型参数估计

实际中主动声呐的波束域数据中往往同时包含有混响、杂波与噪声，本文将杂波K分布和噪声Gamma分布进行结合，提出主动声呐的K-Gamma混合分布。表达式如下：

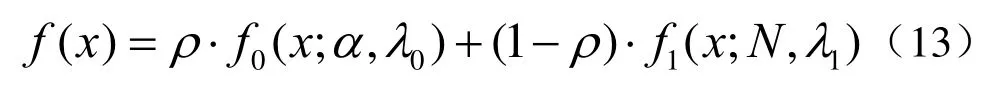
式中，ρ表示混合因子；f0(x;α,λ0)表示K分布，α、λ0分别为K分布的形状参数和尺度参数；f1(x;N,λ1)表示Gamma分布，N、λ1分别为平滑点数和指数分布参数。

2.1 基于zlnz方法的K分布形状参数估计

文献[7,8]提出了多种K分布形状参数估计方法，并对它们的估计性能作了比较。本文采用基于Blacknell等提出的zlnz方法[9]。在这个方法里，形状参数由下式得到：

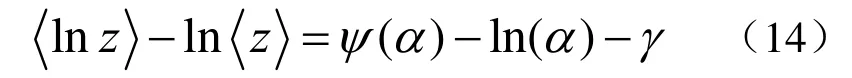
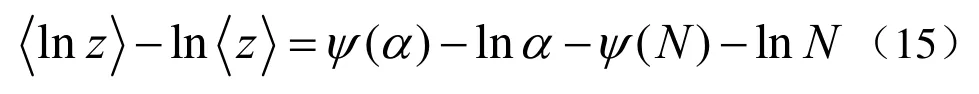
对于N点平滑的K分布（强度），下面的关系成立：

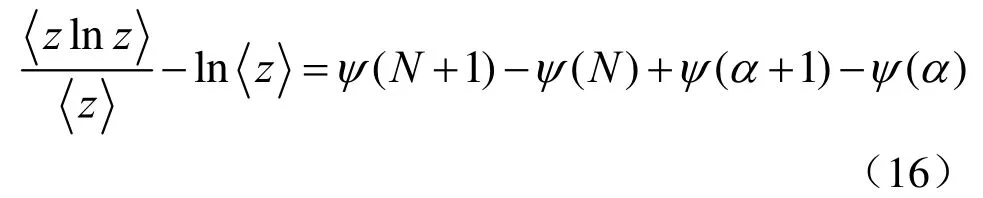
又

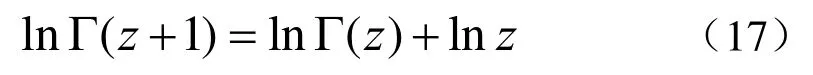
则

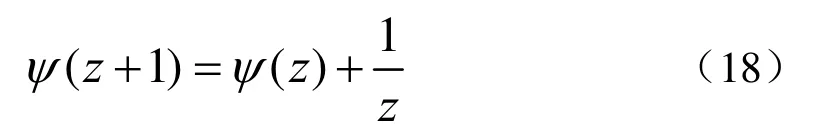
利用式（18），式（16）可以简化为[10]：

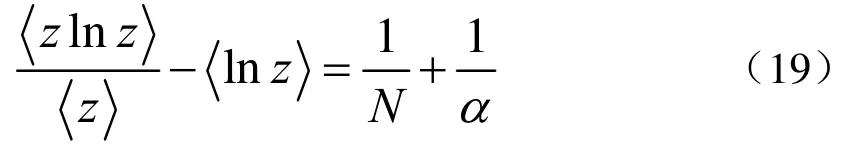
相应的尺度参数估计如下：

2.2 混合因子的估计

根据K分布模型的研究，其形状参数越大，模型越接近指数分布。因此可基于形状参数构造混合因子，使得：（1）数据中的形状参数估计值较大时，提高Gamma分布的权值；（2）数据中的形状参数估计值较小时，提高K分布的权。具体地如下式：

混合分布PDF为

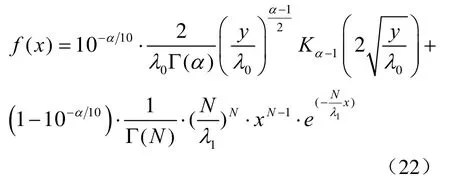
3 试验数据验证及模型应用

为验证K-Gamma混合分布模型的有效性，选取2017年冬季中国东海高分辨主动声呐采集的浅海水声试验数据进行分析。对该组数据进行主动平滑处理的点数为8，指数分布参数为1（背景归一化处理后）；基于zlnz估计的K分布形状参数为1.65，尺度参数为0.658；按式（22）计算后，得混合因子为0.684；整理该组数据的混合分布模型参数值，见表1。

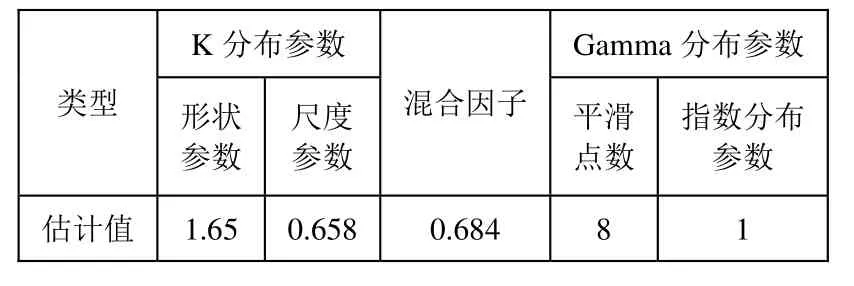
表1 基于该组数据估计的模型参数

根据表1的混合模型参数值，绘制实际数据、Gamma分布、K分布以及混合分布模型在不同检测门限时对应的检测虚警概率曲线，如图3所示。从图中可以看出：（1）当检测门限小于3 dB时，基于K分布与Gamma分布计算的目标检测虚警率虽接近实际数据，但次于混合分布模型；（2）当检测门限高于3 dB时，基于Gamma分布计算的目标检测虚警率严重偏离实际数据，而基于K分布计算的目标检测虚警率虽相对接近实际数据，但也次于混合分析模型。那么，本文提出的K-Gamma混合分布模型，相对于K分布和Gamma分布，与实际数据更加匹配。

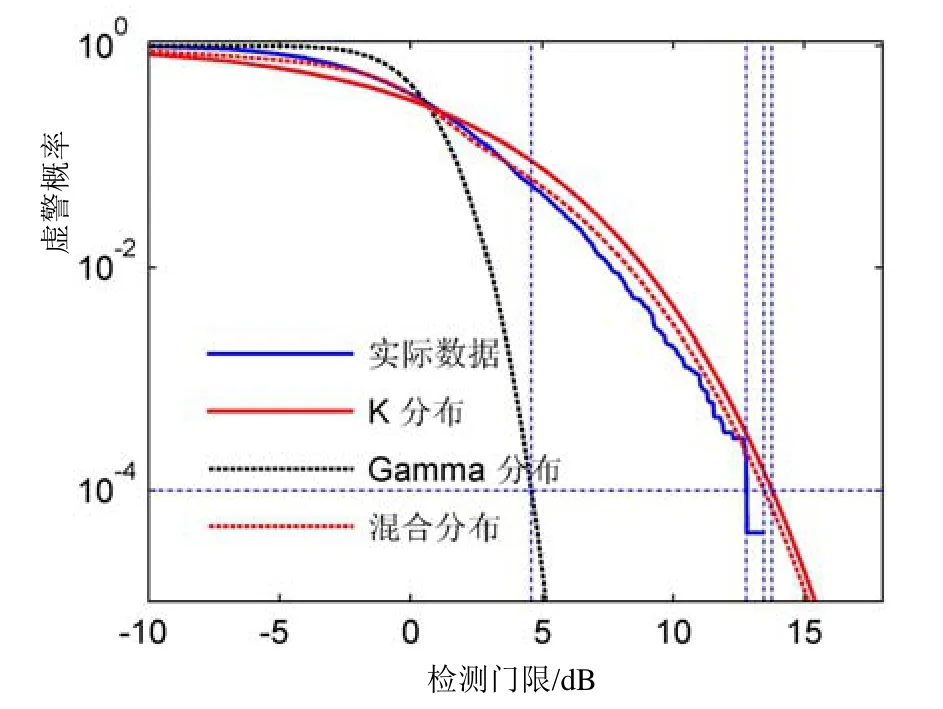
图3 不同检测门限对应的虚警概率

主动声呐目标检测中，通常以某一恒定虚警概率设计检测门限，当信号强度高于检测门限时，判定目标存在；当信号强度低于检测门限时，判定目标不存在。根据图3，假设系统虚警率设计为0.000 1，Gamma分布、K分布、混合分布模型下的检测门限分别为4.6 dB、13.8 dB和13.5 dB；相应地，在转换前，归一化能量的检测门限分别为2.9、24.0、22.4。

为直观呈现K-Gamma混合分布的恒定虚警率实现，绘制实际数据和Gamma分布、K分布、混合分布的检测门限，如图4所示。图中，纵坐标表示归一化能量（无量纲），Gamma分布的检测门限为2.9，K分布的检测门限为24.0，K-Gamma混合分布的检测门限为22.4。

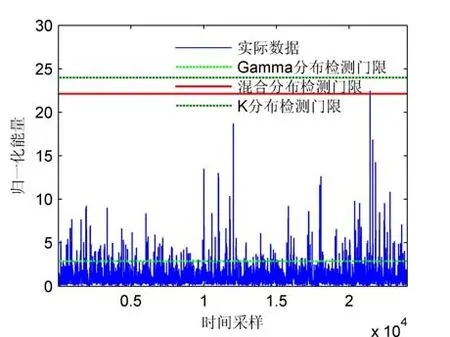
图4 三种方法的检测门限在实际数据中的检测虚警性能

可以看出，当设计虚警率为0.000 1时，基于Gamma分布模型的信号检测门限在该组实际数据中的目标检测虚警数众多，远高于万分之一，使得操作人员难以在众多的虚警中辨别真实目标；基于K分布模型的信号检测门限在该组实际数据中的无检测虚警，检测门限相对较高，使得目标漏检的可能性增大；基于K-Gamma混合分布模型的信号检测门限在该组数据中出现了一次虚警，其实际实现的虚警率接近设计值。因此，K-Gamma混合分布模型较K分布及Gamma分布能够更准确的实现主动声呐系统设计的虚警率。

4 结论

本文分析了包含有混响、噪声以及杂波的主动声呐目标探测数据及其统计特性，提出了基于K-Gamma混合分布模型的高分辨主动声呐目标检测方法。理论分析和实际数据处理验证了所提方法的有效性，该方法应用于低频大孔径主动声呐混响中的目标检测，实际虚警率与设计虚警率相接近。如何精细化的构建混响与杂波中目标信号的PDF，结合本文提出的非目标PDF，应用于主动声呐目标序列似然比检验是很有意义的研究方向。