基于相机与摇摆激光雷达融合的非结构化环境定位

俞毓锋 赵卉菁

面向非结构化环境的轮式移动机器人在民用及国防等领域有着重要的应用需求,其技术发展得到了一些著名赛事的验证和推广(如美国DARPA 无人车挑战赛1http://www.darpa.mil/ grandchallenge05/,欧洲ELROB室外机器人比赛2http://www.elrob.org/,国内跨越险阻地面无人系统挑战赛3http://www.mod.gov.cn/power/2016-10/18/content 4748815.htm等),获得了社会各界的广泛关注.

精确定位作为机器人导航的关键,在室外非结构化环境面临巨大挑战.环境复杂多变、光照、遮挡、缺乏结构化信息等,为视觉里程计[1]或视觉SLAM[2]算法的特征提取与匹配带来很多不确定性,影响定位精度和鲁棒性.另一方面,激光雷达已被广泛应用于机器人系统.基于三维激光雷达[3]的定位系统有较高精度,然而传感器系统昂贵,限制了其广泛的应用.通过电机带动单线激光雷达旋转所构建的三维扫描系统成本较低,但完成一次三维扫描的周期长,如何对周期内的扫描数据进行运动补偿成为其关键因素.文献[3]采取stop-scan-go 的方式,将数据扫描与机器人运动分离,严重影响了机器人运动的连续性;文献[4]利用航位推算法对周期内扫描数据进行运动补偿,仅适用于平坦地形环境;文献[5]利用空间中直线和平面等强结构信息对激光特征进行约束,无法应用于非结构化环境.为了弥补单一传感器信息的局限,融合相机与单线激光雷达的方案也被研究.文献[6−7]利用激光数据构建三维点云,为图像中的特征点赋予深度信息,从而提高定位精度.然而三维点云的重建精度受到累计定位误差的影响,长时间运行过程中特征点深度信息难以准确估计.另一方面,前述研究中均未考虑到由于系统、光照、遮挡等因素对特征点提取与匹配所带来的不确定性影响.

本文提出一种基于相机与摇摆激光雷达融合的定位算法,重点解决在非结构化环境中的机器人位姿估计问题.本文结合激光雷达的深度信息和图像的颜色纹理信息,构建在时序帧间的特征点匹配关系;引入一种置信度评价方法,结合系统误差、数据关联、物体遮挡、特征跟踪等因素对特征点及其匹配关系进行评估,减少低质量特征的影响;最终将定位问题转化为特征点对的加权重投影误差优化问题予以解决.利用小型轮式移动机器人在越野和公园等典型非结构化环境下进行数据采集和定位实验,验证了本文算法的有效性.实验结果表明,与前沿的双目视觉定位算法相比,本文算法可有效提高在非结构化环境中的定位精度.

本文结构如下:第1 节围绕室外机器人的定位问题调研国内外研究现状,并分析关键技术难点;第2 节给出本文的问题定义,将定位问题转化为特征点重投影误差优化问题;第3 节介绍在时序帧间的特征点匹配关系构建方法,包括从激光到图像,图像到激光等两类匹配方法;第4 节针对系统误差、数据关联、物体遮挡、特征跟踪等不确定性因素,建立特征点置信度评价方法;第5 节给出实验结果与分析,包括越野和公园等两类典型非结构环境的定位结果,与航位推算法,单目或双目视觉定位算法的精度对比,以及置信度评价的有效性分析等;第6 节给出总结和今后的研究展望.

1 相关研究

目前的无人车或室外移动机器人大多依赖于高精度卫星定位与惯性导航组合系统(俗称GPS 惯导)并结合轮速仪等设备实现定位.然而在复杂路面,基于轮速仪的航位推算有很大误差,而卫星信号的遮挡,干扰等严重影响卫星定位精度.通过匹配相机,激光雷达等采集的环境信息进行定位,可提高无人车或移动机器人在复杂环境中的定位精度.

视觉里程计[1]作为一个通用视觉定位算法,利用前后帧特征点的检测跟踪结果,解算机器人实际行走里程.由于缺乏深度信息,单目视觉里程计无法有效地解算尺度,成为定位误差的重要原因之一.双目相机系统[8]在两个相机标定准确的前提下,利用左右图像生成三维点.图像中的二维特征点有唯一的三维点进行对应,减小了求解三维深度的误差,但相机之间的对应点匹配受到环境光照、阴影等因素影响,在光照条件受限的情况下,容易产生定位偏差.

不同于相机,激光雷达传感器主动发出激光束进行测距,受到光照的干扰小.在地面平坦的区域,直接使用水平放置的二维激光雷达即可进行定位[9].在地面起伏明显区域,三维激光雷达可通过点云匹配实现较高精度的定位[3],但传感器价格昂贵限制了这类方法的应用.为了构建低成本三维扫描系统,一些研究者将二维激光雷达安装在旋转电机上构建低成本三维扫描系统.然而这类系统完成一次三维扫描的周期长,需对周期内的扫描数据进行运动补偿.Stop-scan-go 的方式将数据扫描与机器人运动分离,虽避免了扫描周期中的运动影响,但严重影响了机器人的运行速度[4];航位推算法对运动的补偿可在平坦路面得到较高精度,但无法适用于非平坦路面[5];空间中直线和平面等强结构信息可对激光特征进行约束来估计扫描周期内的运动,但环境的结构假设过强,无法应用于非结构化环境[10].

在单一传感器无法有效定位的情况下,多传感器融合的定位方法可提高传感器信息量,成为解决定位问题的一个可行途径.一些研究者使用多个不同朝向的单目相机进行融合定位[11],将一个相机向下倾斜观察地面,一定程度上减少了光照的影响.另一些则在单目或双目视觉定位系统中加入惯性导航单元,有效减少角度误差[12−13],从而提高定位精度,但仍然无法避免光照、遮挡等因素干扰下,低质量特征点对定位结果的影响.相机与激光雷达两类传感器的融合可有效提高特征的信息维度.传统相机与激光雷达融合定位算法主要依靠激光传感器生成的三维点云对图像中特征点的深度进行估计,再使用视觉特征进行定位[6−7],提高定位精度.然而,受到非结构化场景中地面颠簸的影响,三维点云重建结果随着时间的推移存在明显累计误差,长期运行的偏差很大程度影响定位结果,需考虑直接在局部帧间进行相机和激光雷达特征层上的匹配.另一方面,相机和激光雷达在融合时引入了更多系统误差,容易造成错误匹配,需要分析特征的置信度给出权重,剔除误差较大的特征点.

综上,面向轮式移动机器人室外非结构化环境的精确定位,本文提出一种基于相机和摇摆单线激光融合的视觉定位算法,构建在时序帧间的特征点匹配关系,并引入一种结合系统误差、数据关联、物体遮挡、特征跟踪等因素的置信度评价方法,最终将定位估计转化为特征点对的加权重投影误差优化问题予以解决.

2 问题定义

机器人与相机为刚性连接,两者的坐标系可以通过外部标定参数进行转换.因此,机器人的定位求解等价于相机的定位求解.定义相机坐标系为基准坐标系,图像帧率作为基准帧率,第k帧图像所对应的相机坐标系记为Ck,对应的图像坐标系为Ik.由于激光与相机的帧率不一致,将激光帧与最接近的图像帧进行对应.假设激光帧l上的一个激光点所对应的图像帧为k,令三维激光点在基准坐标系(相机坐标系)下定义为P k,对应的二维图像上的点为pk=KP k,其中K为相机的内参矩阵.

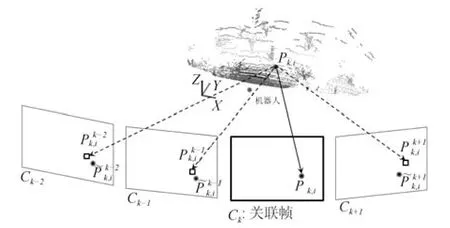
图1 问题定义Fig.1 Problem statement

如图1 所示,(P k,i,pk,i)表示在第k帧下第i个特征匹配点对.一方面,通过跟踪图像点pk,i,可获得其在相邻帧上的图像跟踪点,j=···,k −2,k −1,k,k+1,···.另一方面,三维激光点P k,i可通过坐标变换投影至对应帧j.令Mk表示第k帧的相机坐标系Ck到世界坐标系的坐标变换矩阵

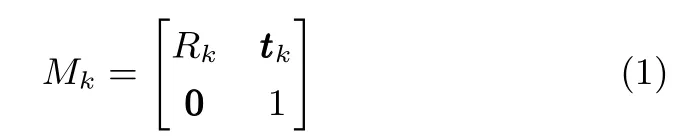
其中,Rk为3×3 的旋转矩阵,tk为平移向量.P k,i可先转换至世界坐标系MkP k,i,再转换至第j帧的相机坐标系Cj下最后投影到第j帧的图像坐标系Ij,得若定位无误差,且特征对应与跟踪准确,则在第j帧图像上,基于图像特征点跟踪的结果和基于坐标系转换的投影结果为同一点.由于定位误差的存在,或特征对应与跟踪时的误差影响,跟踪点与投影点之间存在偏差.定义第k帧中的第i个特征在第j帧中的跟踪点与投影点之间的偏差为特征的重投影误差,即

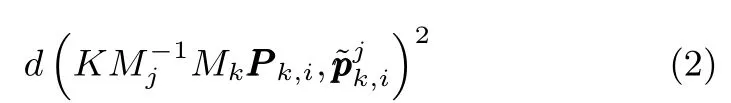
当特征对应与跟踪准确时,通过最小化重投影误差,可进行定位,即

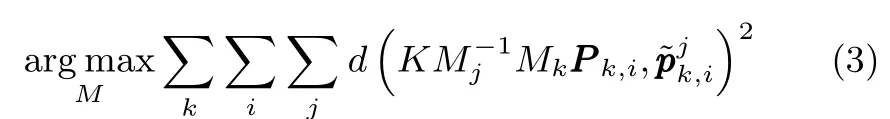
针对特征对应与跟踪的误差影响,假定误差噪声为白噪声,通过置信度估计方法调整各个特征的权重,减少甚至消除特征误差的影响.因此,在最小化重投影误差函数中加入权重参数,定义为

上式中所有的坐标系变换矩阵M都需进行优化.随着帧数的逐渐增加,优化也会越来越慢.实际上,在线定位系统无需对过早的信息进行优化,只需优化当前一小段时间内的定位结果.因此,最终所需优化的代价函数如下优化的过程为非线性优化,可使用LM 算法(Levenberg-Marquardt[14])进行迭代优化.综上,本文定位算法整体框架如图2 所示.

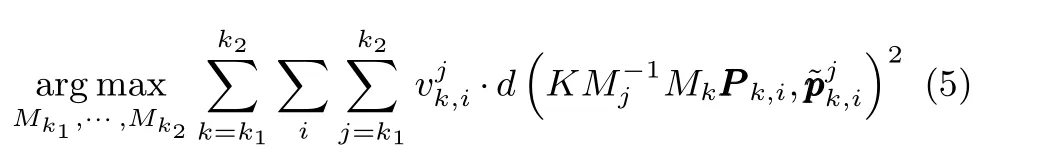
图2 系统流程Fig.2 System overview

1)对于第k帧图像,已知k −1 帧图像的特征点集{pk−1,i}与对应三维点集{P k−1,i},通过跟踪图像特征点得到当前帧图像特征点集

3)通过插值生成k帧图像相邻激光帧的位姿,并将激光点投影至对应帧,构造最新的激光点与图像点特征对应;

4)使用局部若干帧图像,通过优化代价函数(5),优化当前时刻附近的相机位姿.

在上述四个模块中,模块一图像特征跟踪部分可使用任意的特征点跟踪方法;模块二当前帧的位姿预测使用当前帧的最小化重投影误差方法,本质上与模块四一致,而优化方法可使用开源的非线性优化方法.因此,本文的重点内容在于求解模块三的特征对应与构造模块四的优化函数(5).这两部分内容分别在第3 节特征对应求解和第4 节置信度估计中详述.

3 特征对应求解

三维激光点与二维图像点的特征对应关系包含以下难点.1)三维激光点在对应帧的投影很可能是一个无特征或特征较少的区域,投影点可能无法跟踪或跟踪误差很大;2)三维激光点云非常稀疏,且一帧图像所对应的激光数据也只集中在图像中的一小块区域内,如果仅使用三维点到二维点的投影,则特征过少且过于集中.因此,在特征对应中不仅需要考虑三维激光点到二维图像点的正向对应,还需要考虑二维图像点到三维激光点的逆向对应.本文特征对应同时包含激光雷达到图像(三维到二维)和图像到激光雷达(二维到三维)两部分内容.

3.1 激光雷达到图像的对应

给定一个在第k帧的三维激光点P k,i,通过标定参数与局部运动估计,可投影至相邻某帧j帧中,得到投影点假定标定与同步的参数准确,其对应帧k的图像投影点即为真实k帧图像的特征对应点pk,i.如果对应帧投影点为图像特征点pk,i,则可直接进行图像特征点跟踪,获取在j帧的跟踪点跟踪点与投影点即为投影点P k,i在第j帧的特征对应,代入式(5)中进行定位.

如果对应帧投影点pk,i本身所包含的特征信息较弱,直接对其进行图像特征跟踪会产生较大误差.为了解决这一问题,可采用如图3 所示的处理方法.假定图像特征点pk,1,···,pk,n为激光投影点pk,i的邻近点,通过邻近点的跟踪,可获得投影点的跟踪.假定为这些邻近点在第j帧的跟踪点,投影点pk,i在第j帧的跟踪点可以通过线性插值求解,得同时建立在第j帧的投影点与跟踪点的对应关系

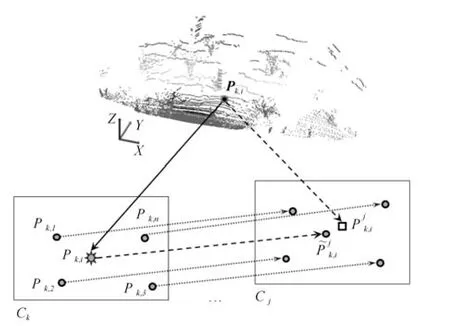
图3 激光特征点到图像的对应求解Fig.3 LiDAR-to-camera correspondence generation

3.2 图像到激光雷达的对应

由于三维激光点的稀疏性,三维激光点到二维点的对应数量较少,仅使用这些对应点很难进行定位求解.而图像的特征点更为稠密,利用图像到激光雷达的特征对应,可有效地提高特征点数目.

如图4 所示,给定第k帧图像上的一个特征点pk,i,需找到其在三维上的对应点.通常情况下,由于激光点的稀疏性,图像特征点无法直接与激光点对应,因此需通过插值求解.对于第k帧图像,假设相邻一段时间内[k1,k2]的激光点投影到图像Ik上,根据其扫描规律,不同帧的激光点处于不同的区域.图4 所示的一帧激光的投影点可形成一个区域.在此区域内,可忽略激光点之间的同步误差.对于图像Ik上的点pk,i,其邻近点均为第j帧所对应的激光点投影对应的三维点为P j,1,···,P j,n.通过拟合三维点形成平面或曲面,再根据平面与图像点所对应射线的角点,即可求解出pk,i到第j帧的三维对应点P j,i.将其投影到其他帧,可以得到对应的投影点另一方面,图像特征点pk,i也可跟踪至帧,得到对应的跟踪点最终建立第k帧图像特征点在第帧的跟踪点与投影点之间的对应,代入式(5)中进行定位.

4 置信度估计

特征对应存在不同程度的误差,给定一个特征对应,其误差来源可分为以下四个方面:

1)硬件系统误差(vh),包括激光雷达与相机的标定与时钟同步误差;

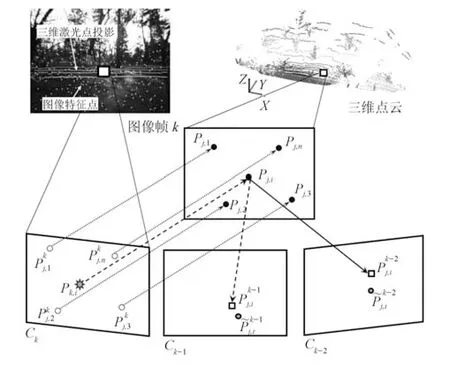
图4 图像特征点到激光的对应求解Fig.4 Camera-to-LiDAR correspondence generation

2)数据关联误差(vf),包括数据插值误差与不同源数据间投影的误差;

3)物体遮挡影响(vo),为两个传感器视角不同产生遮挡导致的误差;

4)特征跟踪误差(vt),包括单个图像特征点跟踪误差与多个特征点联合跟踪误差.

通过以上四个方面的置信度分析,定义特征对应综合置信度如下:

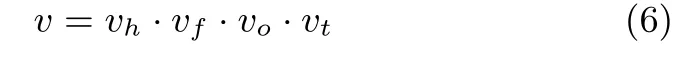
4.1 系统标定与同步

对于一个使用多传感器的系统,标定误差和时钟同步误差无法避免.因此,系统置信度vh包含相机与激光之间的标定产生的置信度vh(c)与时钟同步产生的置信度vh(s).

相机与激光之间的标定参数包含旋转矩阵R和平移向量t,其相对误差分别为eR和et.对于一个激光扫描结果,投影到电机所在坐标系下为P=[X,Y,D]T,转换到相机坐标系下的过程中,旋转和平移误差产生不同的效果.旋转标定误差所带来的实际误差与距离D成正比,而平移标定误差所带来的实际误差为定值.因此,标定置信度函数建立如下:

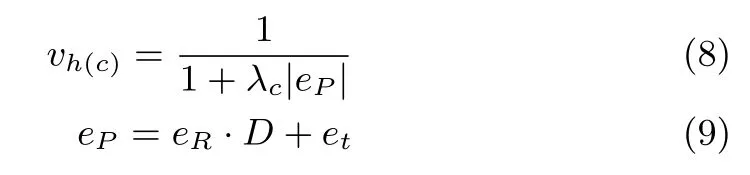
激光雷达与相机有不同的扫描频率,为了将两个数据进行融合,需要进行插值.在插值的过程中,两者时间相差越大,所带来的误差也越大.因此,同步置信度定义如下:

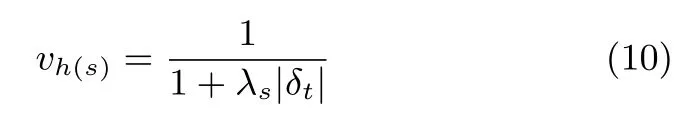
4.2 数据关联

本文算法所述的特征对应求解包含激光雷达到图像(三维到二维)和图像到激光雷达(二维到三维)两部分.一方面为了将两者放入同一个目标函数下,另一方面由于激光点的稀疏性所带来的插值误差以及图像投影点的低纹理性带来的跟踪误差,需进行数据关联上的置信度估计vf.

在三维激光点到二维的对应求解上,给定一个第k帧的激光点P k,i,如果对应投影点pk,i为图像特征点,那么两者进行直接关联,置信度为1.如果对应投影点pk,i不是图像特征点,需找到邻近区域的特征点pk,1,pk,2,···,pk,n,用这些特征点的跟踪实现投影点的跟踪.在数据关联置信度上,通过计算投影点周围一小块图像块的纹理特征显著度来决定置信度的大小.我们以3×3 区域内的梯度与亮度值作为描述子,比较投影点pk,i与投影点周围像素之间的相似度,加权平均得到平均相似度¯s.置信度定义如下:

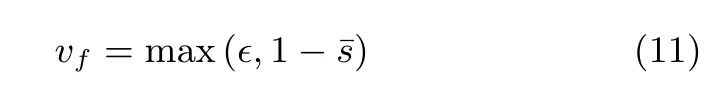
在二维图像点到三维点的对应求解上,给定一个第k帧的图像点pk,i,如果需要通过插值第j帧的激光点得到对应三维点,那么就包含同步以及插值误差.同步误差包含在系统置信度中,因此只需考虑插值所产生的误差.在对应点求解的过程中,我们采用平面拟合的方式确定三维点所在平面,并通过平面与图像点对应射线的交点来确定三维点.因此,平面拟合的准确度就决定了三维点的置信度.我们假设在拟合平面后,这n个三维激光点与平面的距离分别为d1,···,dn,则数据关联的置信度与距离的均方相关,定义为:

4.3 物体遮挡

由于激光扫描仪与相机的视角不同,以及环境内移动物体的干扰,激光与相机的数据关联上可能产生错误匹配.图5为数据示例.左上图为相机图像,左下图为激光投影到图像中的结果.在正确标定的基础上,观察立柱上的激光点,有部分点偏离立柱,原因是激光与相机在水平位置上有偏差(激光偏右),导致两个传感器所观察到的内容有所不同.图5 右图为对应示意.其中圆形点为激光和相机正确匹配的点,方形点为错误匹配的点,包含激光扫描到前景,而相机看到背景的点;以及激光扫描到背景,相机看到前景的点.从图中可以看到,物体边界处所带来的遮挡影响较大,因此以局部深度差作为置信度估计的相关量.

给定一个图像点p,令其对应激光点为P,并且深度值为D.假设是图像点周围一小块区域内激光点的平均深度值,物体遮挡的置信度vo与深度差相关,定义为:

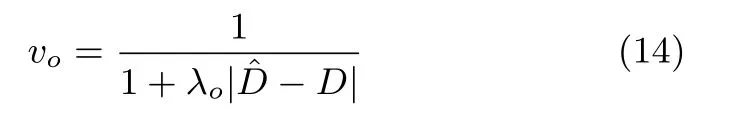
4.4 特征跟踪

对于一个三维激光点P k,i,其对应帧的二维投影点为pk,i.如果pk,i是一个特征点,那么在第j帧上的跟踪点是直接通过特征跟踪得到.跟踪所得的匹配度sc即为特征跟踪置信度vt.

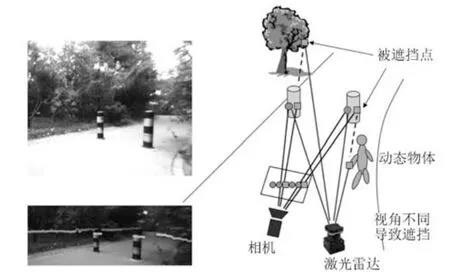
图5 数据融合时,传感器视点不同造成的物体遮挡示意Fig.5 Example of occlusion in camera-LiDAR fusion caused by different point of view

如果投影点pk,i所在区域为非特征点区域,需由投影点临近的特征点进行跟踪.令pk,1,···,pk,n为周围的图像特征点,在第j帧中,跟踪这些图像特征点,并插值生成的投影点pk,i在第j帧上的跟踪点如图3 所示.影响跟踪置信度的因素包含邻近点的跟踪置信度以及邻近点相对位置的稳定性两方面.定义scx为第x个临近特征点的跟踪匹配度,dx,k为第x个邻近点在k帧中与投影点的距离.由于在机器人运动过程中,图像特征点尺度变化明显,邻近点的绝对位置变化较大,但相对位置稳定,因此定义相对距离比例

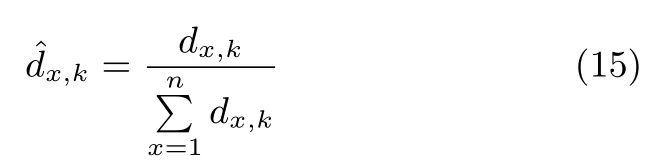
跟踪置信度vt定义如下:

5 实验结果

5.1 概述

实验使用小型轮式机器人作为实验平台,在越野和公园两个典型非结构化环境进行实验,如图6 所示.平台所含设备包括一个Bumblebee 双目相机,一个Hokuyo 单线激光(UTM-30LX),一个旋转电机,一个单点GPS,一个低精度IMU 和轮速编码器等.其中,单点GPS 在所述实验环境无法收到卫星信号,因此未在实验中使用.Bumblebee 双目相机的分辨率为1 024×768,最高帧率为18 Hz.单线激光水平扫描视场角为180 度,角分辨率为0.5 度,帧率约为37 Hz.电机带动单线激光进行上下周期性摇摆运动,周期约为2 秒.实验过程中,机器人通过手动遥控的方式进行控制.考虑到电机摇摆周期的限制,实验过程中机器人速度不超过1.2 m/s,在转弯时,机器人速度不超过0.5 m/s.

实验采用本文提出的相机和摇摆激光的融合定位算法,并考虑了式(6)所述的四项置信度.其中系统和数据关联置信度联合定义为S,物体遮挡置信度定义为O,特征跟踪置信度定义为T.实验比较了本文算法与双目libviso[15]视觉里程计算法,单目或双目orb-SLAM[2]算法和航位推算法(odom)等定位算法的精度误差,说明定位结果的有效性.其中双目libviso 通过左右相机的特征点匹配,生成单帧的三维点云,并通过前后帧的特征点匹配,计算帧间位姿估计.算法只包含前后帧的匹配定位,不包含多帧捆集调整.orb-SLAM通过orb 特征,先匹配前后帧特征点生成帧间位姿估计,再通过局部的捆集调整优化位姿估计,最后间隔一定帧数选取关键帧,生成词袋模型用于闭环检测.本文提出的融合定位算法通过相机与激光雷达的特征对应,最小化局部重投影误差进行帧间位姿估计.算法利用激光雷达的距离信息生成局部三维点云,并将特征点投影至相邻图像帧上用于特征对应与位姿估计,不显式生成三维点云地图.因此,算法只进行局部帧间位姿估计,不通过地图进行闭环检测.

图6 非结构化环境和机器人平台Fig.6 Off-road environments and robot platform

为保证各个定位算法所使用数据的一致性,实验采用数据仿在线回放的方式进行算法测试.通过数据回放模块,利用同步采集的相机、激光雷达、电机、惯导、编码器等数据,模拟数据采集过程中的传感器数据流,对定位算法进行测试.该测试方式一方面保证了各个定位算法所使用数据一致性,另一方面通过数据回放模块和算法模块的分离,达到仿在线测试目的.

此外,为了说明本文提出的置信度定义对特征点的筛选和定位的有效作用,实验中还对比了添加各类置信度的后特征点数目与定位结果比较.在此,我们定义不加置信度定义的方法为our,添加本文所有置信度内容的方法为our +SOT.在置信度的参数λ上,所有包含λ参数的置信度定义公式,如式(8)等,形式上均为:

当δ=0 时,v=1 置信度最大.随着δ增加,v不断减小.当λ·δ=1 时,v=0.5.在本实验中,采用手工调整λ使得v=0.5 时,δ取到了合适的经验值.具体定义如下:

1)式(8)中λc的经验值为距离D=30 m;

2)式(10)中λc的经验值为时间差δt=100 ms;

3)式(12)中λfI的经验值为距离方差

4)式(14)中λo的经验值为深度差

5)式(16)中λt的经验值为相对距离方差¯d2=0.2.

5.2 特征跟踪与置信度

典型非结构化环境如图6(a)和图6(b)所示,环境无明显结构特性,地面崎岖不平,且光照条件一般.由于车载电脑配置受限,相机的帧率降至5 Hz,相邻的激光帧数据将直接关联到对应图像帧.单数据投影如图7(a)所示.由于激光和相机视角不同,激光的部分观测在图像中被前景遮挡,但在单帧激光数据中无法有效提取(如图7(a)中矩形框区域内,部分激光观测被图像中的树干遮挡).当一次电机上下摇摆周期内的激光点全部投影至同一帧图像中时,可有效地去除被遮挡区域(如图7(b)矩形框区域所示),生成物体遮挡置信度图O.

图7 激光点投影到视频结果Fig.7 Projection results of LiDAR points

特征置信度估计是本方法的另一重要因素.图8 所示为特征跟踪与置信度估计结果.所示特征点的大小表示跟踪时间的长(越大表示跟踪越久),而亮度则表示置信度短(越亮表示置信度越高).从图中可以看出,特征点主要集中在图像中下方区域,也是机器人导航的最重要区域.

图8 特征跟踪与置信度结果Fig.8 Feature tracking and confidence measure results

5.3 定位结果

5.3.1 越野环境

越野实验环境如图6(a)所示,越野环境地面起伏不平,光照条件较差.由于非结构化环境下轨迹真值标注的困难性,实验顺时针行驶一段约35 米的闭合轨迹,以轨迹首尾的闭合误差作为度量方式.比较航位推算法(odom),orb-SLAM(含单目orb-mono 和双目orb-stereo),双目libviso(viso-stereo)和本文含置信度估计的融合定位算法(our+SOT)等方法结果,如图9 所示.

在图9(a)所示二维闭合误差上,航位推算法在地面起伏不平的路面下精度较低,闭合误差大;单目视觉定位算法由于不包含尺度信息,闭合误差较大;本文相机与激光融合定位整体轨迹与双目视觉定位算法类似,在轨迹首尾闭合精度上略高于双目视觉定位算法.考虑到越野环境的三维运动,仅使用二维闭合误差无法准确衡量定位的精度.因此,实验还对比了各个方法之间的高度(Z)值,如图9(b)所示.从图中结果来看,本文算法在最终高度闭合估计上优于其他算法(如图中点虚线所示).

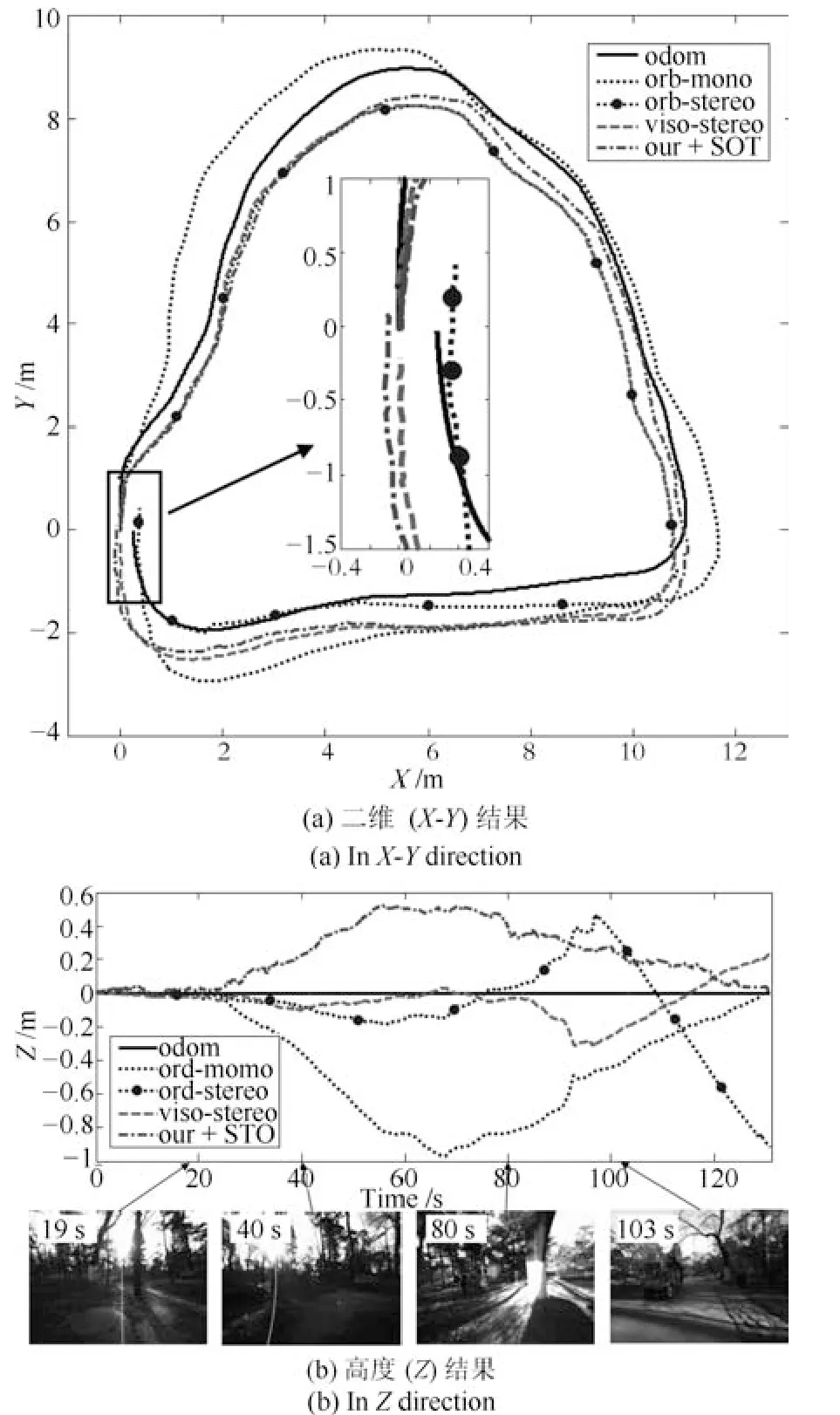
图9 越野环境定位结果Fig.9 Localization results in off-road environment

5.3.2 公园环境

公园环境如图6(b)所示,相比于越野环境,公园环境路面平整度增加,加强了运动约束,但行人较多,给特征点的对应带来更多干扰.实验车逆时针行驶一段约250 米的闭合轨迹,结果如图10 所示.

从图10(a)中的二维闭合误差处分析,航位推算法由于地面起伏,闭合精度无法有效提高;单目视觉定位算法无法有效保证全局尺度的一致性,带来较大定位偏差;viso-stereo算法在第一次拐弯后误差一直增加,最终的闭合误差超过10米;orb-stereo 算法虽然在闭合上精度上较高,但第一次拐弯处的形状与其他方法有很大偏差;本文方法结果在整体形状上与其他的多数方法类似,最终闭合精度略高于orb-stereo算法.

从图10(b)中高度信息进行分析,整体轨迹起伏明显,达到10 米以上.本文算法与orb-stereo 虽然在闭合处高度接近,但机器人在p1至p2间行驶的过程中大致在平路上,而orb-stereo 高度结果产生明显起伏.

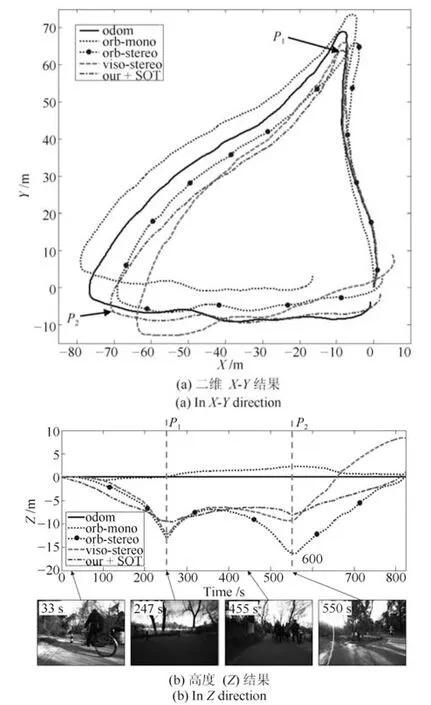
图10 公园环境定位结果Fig.10 Localization results in park area

5.3.3 数值结果分析

通过比较闭环起始点和终止点之间的偏差,定量分析定位精度,两组实验的数值结果如表1 所示.航位推算法无法估计三维精度,在二维精度上与双目定位算法相似.单目视觉定位算法由于尺度估计不准确,偏差较大,尤其是公园环境.在越野环境中,viso-stereo 精度较高;在公园环境中,orb-stereo 精度较高,原因可能是libviso 的特征描述子受到光照干扰较小,而orb-SLAM 具有三维重建与定位优化,行人的影响较小.本文算法在两处实验的精度均高于双目视觉定位算法,说明了算法的有效性.

表1 不同定位算法闭合误差(m)Table 1 Results of different localization algorithms(m)

5.4 重投影误差与定位结果相关性

本文使用最小化重投影误差的方式估计机器人位姿,并使用特征的置信度估计对特征进行约束.为了证明重投影误差与定位结果的相关性,在越野环境实验中,我们对不同算法的重投影误差和定位结果进行整理,结果如表2 所示.此处,硬件系统和数据关联置信度统一为系统置信度,记做S,物体遮挡置信度记做O,特征跟踪置信度记做T.

表2 重投影误差与定位结果相关性Table 2 Correlation of re-projection errors and localization error

首先,对于双目定位结果(orb-stereo 和viso-stereo),由于激光与相机本身存在标定与配准误差,而定位结果(双目)和用于重投影误差解算的传感器(单目+激光)不一致,导致重投影误差较大.对于本文基准算法,即不加任何置信度估计的算法,特征点数目与双目结果接近,平均重投影误差比双目小,但定位误差却更大,原因是激光雷达与视觉融合的系统误差比双目系统高.在加入系统误差置信度分析后(our+S),特征点数目少量减少,重投影误差也相应减少,定位误差也随之略微减少.通过逐渐加入遮挡置信度(O)和跟踪置信度(T),整体特征点数目减少至244.52,重投影误差减少至3.40,定位误差减少至0.109 米,与双目系统相比有了显著的提高.

综上,尽管激光雷达与相机融合定位系统的硬件误差比双目相机大,在加入置信度分析后,基于相机与激光的定位算法减少了无效的特征点数据,有效地减少了重投影误差,提高了定位精度.

6 总结与展望

针对非结构化环境的定位难点,本文提出了一种基于相机和摇摆激光雷达融合的定位算法.算法结合激光雷达的深度信息以及图像中的颜色纹理信息,通过激光雷达到图像,图像到激光雷达的两种映射,构建在时序帧间的特征点匹配关系;引入一种结合系统误差、数据关联、物体遮挡、特征跟踪等因素的置信度评价方式,量化评价特征点匹配中的不确定性,最终将定位问题转化为特征点对的加权重投影误差优化问题予以解决.

实验利用小型轮式移动机器人在越野和公园等典型非结构化环境下进行的数据采集和结果分析,对提出的基于相机和摇摆激光雷达融合的定位算法进行验证.结果表明,与前沿的单目或双目视觉定位算法相比,本文算法可提高在非结构化环境中的定位精度.与此同时,实验还进行置信度与定位精度的相关性分析,说明本文置信度评价方法可有效地抑制数据融合,特征提取与匹配等不确定性因素对定位精度的影响.

考虑到在不同环境(包括路面、卫星定位、环境特征等条件)不同定位方案各有其优劣,后续的工作将研究基于环境评估的环境自适应融合定位解决方案.另一方面,由于激光摇摆周期过长,一定程度上限制了机器人的移动速度,尤其是转弯速度,今后的研究也将尝试摇摆激光的控制中加入反馈机制,确保激光雷达的扫描范围处于最重要的区域内.