基于正则化与时空约束改进K最近邻算法的农业物联网数据重构

吴华瑞，李庆学，缪祎晟，宋玉玲

基于正则化与时空约束改进K最近邻算法的农业物联网数据重构

吴华瑞1,2，李庆学1,2，缪祎晟1,2，宋玉玲3

（1. 国家农业信息化工程技术研究中心，北京 100097；2. 北京农林科学院北京农业信息技术研究中心，北京 100097；3.农业农村部农业物联网重点实验室，杨凌 712100）

针对农业复杂环境易发的物联网感知数据丢失异常问题，该文提出一种基于正则化惩罚的K最近邻数据重构方法（K nearest neighbor-regularization penalty，KNN-RP），采用岭回归方法对最近邻方法中的最小二乘因子进行正则化，并讨论了惩罚项的范数选取形式。通过对农业物联网感知数据的时空稳定性与相关性分析，确定了时间与空间约束矩阵的定义方式。采用温室数据样本对算法性能进行交叉验证，结果显示该文的KNN-RP性能在点丢失模型下优于KNN、反距离加权KNN算法以及DT算法，而在块丢失模型下优于KNN和反距离加权KNN算法，略低于DT算法，提高了农业物联网的感知数据质量。该研究可为基于物联网数据的农业生产决策提供参考。

算法；模型；农业物联网；数据重构；聚类回归

0 引 言

农业物联网是进行农业环境感知、生产决策管理与科研分析等的重要数据来源，其数据的精度与质量对研究与决策结果有着重要影响。由于传感器、网络链路、采集节点等的软硬件故障难以避免，农业物联网存在数据错误、缺失等问题进而降低感知数据质量[1-4]。农业生产监测中环境复杂恶劣、信道条件复杂与网络能量受限等条件与特征均会提高数据异常的概率。不仅如此，随着网络规模的扩大，其故障出现的频率也随之升高[2]。为提高农业物联网监测数据的完整性与质量，有效的数据重构方法是有待研究解决的关键问题。

缺失数据重构方法在许多领域有着重要的作用[5-7]。常见的数据插值重构方法有线性插值法、移动平均法、基于机器学习重构方法与基于压缩感知的数据重构方法等。线性插值法、移动平均法仅适用于线性度较高数据的重构问题，对于农业环境的高度非线性数据这2类方法重构精度较低。同理，多元回归法虽然可以实现非线性数据高精度拟合，但随着数据非线性的提高，该方法的变量数迅速增加，算法复杂度呈指数级增加。基于机器学习的数据重构算法，如K最近邻（K-nearest neighbor，KNN），delaunay triangulation（DT）以及多通道奇异谱分析。这些方法通常仅适用于少数缺失值场景，当缺失值较多时，该类方法的性能下降明显[2]。潘立强等[8]将时间估计方法与空间估计方法（multiple regression，MR）相结合，对无线传感器网络的感知缺失值进行估计，结果显示单纯的时空估计算法对相对平稳信号的估计精度更高。Kong等[2]提出一种面向高数据丢失率的改进型压缩感知与重构方法，并从单参数、多参数角度给出了重构精度分析。Sun等[5]提出了一种面向数据块的稀疏贝叶斯学习算法，利用数据的块属性与固有结构重建变换域的CS稀疏系数进而恢复原始信号。Eldar等[9]根据数据块的相干度量导出了块稀疏信号的不确定关系，并提出正交匹配追踪算法的K-稀疏信号重构方法，利用块稀疏性实现了更好的重构性能。上述研究显示，单一维度的数据时空关联插值与重构方法研究已较为充分，但基于多参数间联系或基于数据块稀疏的重构方法是目前研究的热点[10-12]。在基于压缩感知的数据重构方面也有诸多研究，传统基于静态数据的压缩感知方法难以体现农业物联网数据的动态变化特征，而动态压缩感知算法的高复杂度又较难适用于资源受限的农业无线传感器网络[1,5,13-16]。

综上所述，本文结合农业环境数据的时间、空间、参数间关联特性研究提出一种基于正则化惩罚与时空约束的改进KNN方法，以期提高农业物联网监测数据的重构准确性。

1 农业物联网数据模型

1.1 环境数据重构模型

农业物联网监测应用多采用无线传感器网络（wireless sensor network, WSN）技术，对于WSN数据重构应用场景，一般采用矩阵形式表示重构前后数据，环境参数矩阵（environment matrix, EM）定义为[17-19]

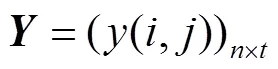
式中为第个节点，为第个时间点。

农业WSN因为软硬件故障或信道链路等问题易出现数据丢失或异常，其中异常数据经异常检测算法检出后删除，也可视为丢失数据一同处理[18]。此时EM矩阵中会出现0值项，则定义数据丢失矩阵（data missing matrix, DMM）表征数据的丢失情况[2,20-21]

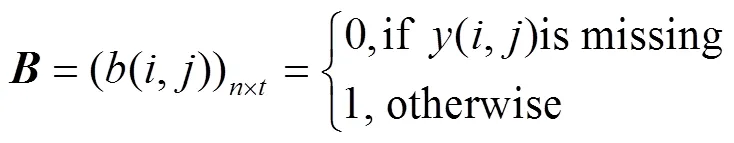
则WSN实际采集到的数据可表示为感知矩阵（perception matrix, PM）

P

=

B

.×

Y

（3）

式中.×表示矩阵对应元素相乘。

农业WSN数据重构方法的目标即是要从采集获得的数据矩阵中恢复出数据矩阵，使其尽可能地接近原始数据矩阵[22-24]。

1.2 WSN数据丢失模型

农业WSN数据采集应用的数据丢失模型主要有其下几种[2,25]：

1）单点随机丢失模型

这是最简单的数据丢失模型。矩阵中的数据是独立随机地丢弃的，即丢失的数据点是随机分布在感知矩阵PM中的。一般WSN的信号噪声和节点接入碰撞是这种模式的根本原因。

2）块随机丢失模型

块随机丢失模型表现为感知矩阵PM中存在部分相邻数据同时丢失的现象，根据丢失数据的相邻排列维度不同主要可分为空间序列块丢失、时间序列块丢失以及参数序列块丢失模型。

其中时间序列块丢失模型为某节点的数据在时间序列上出现频繁丢失，可以表现为持续性丢失和间歇性丢失。在农业WSN应用场景中，不可靠的链路是常见的现象，当链路质量不好时，感知数据易出现时间序列块丢失。

空间序列块模型为某时间节点上相邻节点的数据一同丢失。农业WSN网络拥塞是导致高密度多传感器节点数据丢失的主要原因。

参数序列块丢失表现为某节点多个参数的同时丢失，农业WSN节点传感器硬件故障是造成参数序列块丢失的主要原因。

3）混合丢失模型

在实际应用中一般丢失都由多种因素同时造成，但由于混合模型较为复杂，在具体分析时一般分解为前2种模型进行处理。

2 农业WSN数据重构算法

本文提出了一种改进的K最近邻回归算法以解决农业WSN场景下的缺失数据重构问题。传统的方法多采用时间、空间的关联性进行关联估计，农业场景下的WSN除了上述关联外，其部分参数还具有显著的参数间相关性与周期性。因此，本文方法重点从参数间二阶相关性方面对KNN算法进行改进。以恢复矩阵与原始矩阵尽可能接近为算法优化目标，即

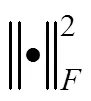
由于农业环境参数的连续时空特性，农业物联网数据在时间与空间维度上展现出明显的相关特性。由图1可以看出，农业物联网不同区域节点数据的变化趋势较为接近，表明WSN节点间参数的高度空间相关性。

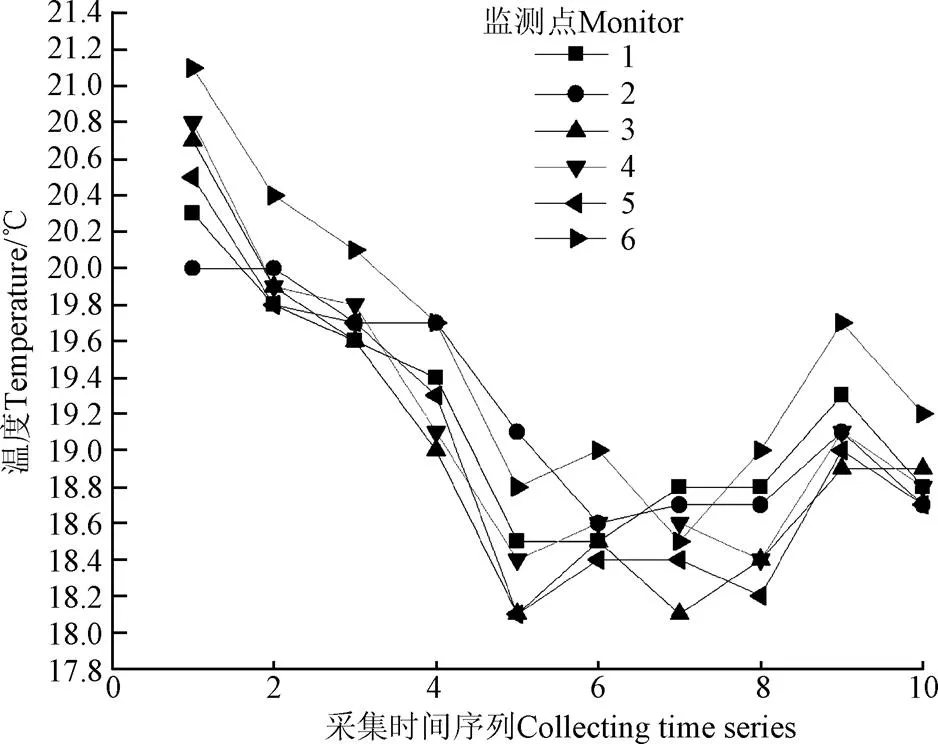
图1 相同时间段不同区域节点的环境温度折线图

由图2可以看出，农业WSN数据的在时间轴上呈现明显的周期性特征，而且如温度、湿度、光照强度等几乎以同一周期进行变化，表明WSN节点间参数的高度时间关联性。

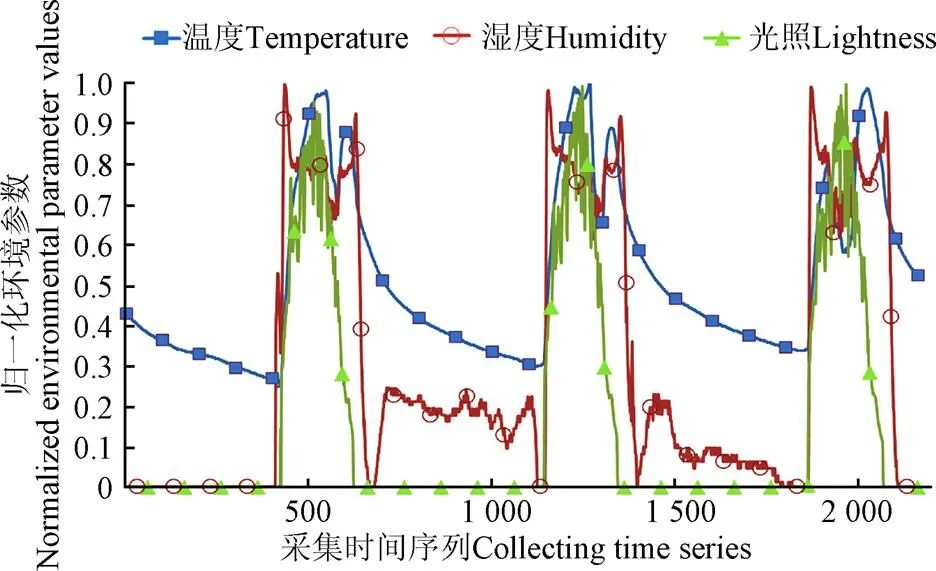
图2 同节点多参数周期变化曲线

在KNN算法之中引入最小二乘法作为损失函数，这里最小二乘模型可表示为

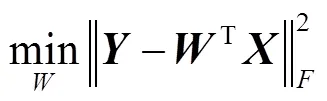
对于最小二乘法的损失函数而言，当不是列满秩，或者某些列之间的线性相关性比较大时，T的行列式接近于0，即为非奇异阵，计算(T)-1时误差会很大，难以保证有唯一的最优解。岭回归是在最小二乘法的基础上引入惩罚项约束，虽然损失了无偏性，但可获得较高的数值稳定性与计算精度。具体为将其主对角元素都加上一个常数，可以使矩阵满秩，满足最优解求解条件。在训练数据较少时带正则化惩罚项的岭回归有较好的效果，于是有[29-30]

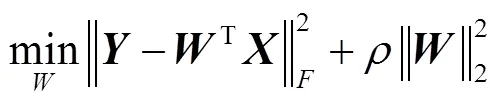
式（6）较式（5）多出的项即为正则化因子，其中是一个大于零的系数，控制惩罚项的力度。采用2范数作为惩罚项虽然可以保证最优解的唯一性，但得出的解未必是稀疏的，会对KNN算法中的取值造成影响而影响结果的稳定性与可靠性，本文采用2,1范数替代。

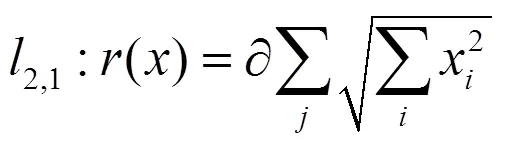
2,1范数较好的融合了1范数的稀疏性特点，又拥有了2范数防止损失函数过拟合的特点，较适用于噪声较大的高维农业WSN数据处理。将式（7）替换式（6）中的2范数，则有

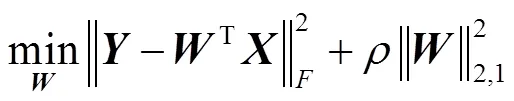
由于式（8）是凸函数，因此，可对w(1≤≤)求导并令其为0，可得

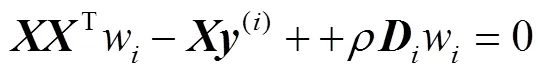
洪子诚先生认为“镜头”即诗的意象，从而对北岛早期诗歌中的意象群展开分析。他提出了两组基本的意象群。一个是作为理想世界、人道世界的象征物存在的，如天空、鲜花、红玫瑰、橘子、土地、野百合等。另一个带有否定色彩和批判意味，如网，生锈的铁栅栏，颓败的墙，破败的古寺等，“表示对人的正常的、人性的生活的破坏、阻隔，对人的自由精神的禁锢。”[5]北岛早期的诗意象的涵义过于确定。到了《触电》这里，我们会发现其意象的设置与北岛早期诗歌有明显的不同。《触电》中的意象，如“握手”，所指不明，与日常生活和传统意象都有距离和阻隔，只给读者一模糊的感知，却难以找到词语明确地与之对应。

将式（9）改变形式可得

基于2,1范数正则化惩罚的KNN算法具体步骤如下：1）将输入的样本数据进行归一化处理；2）按照式（10）对初始阵进行迭代，直至不再变化，此时则为最优的；3）根据式（8）对训练样本数据进行测算，得出最佳的值；4）在步骤3）中得出的值基础上，根据式（8）对测试样本数据进行测算，得出缺失样本的估计值。

如前文所述，农业物联网数据的低秩与时空参关联特性可为数据重构提供关联约束，从而进一步提高预测的准确性。由农业物联网数据的低轶特性可知农业物联网数据矩阵满足

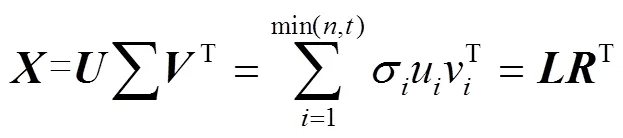
式中和均为酉矩阵，则优化目标可转化为找到一个满足式（3）的T的使得

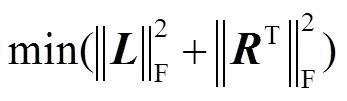
式中、均为初等矩阵。

进一步，考虑到农业生产环境的渐变特性，其参数在时间与空间的变化相对稳定，即在相邻的时间点或相邻节点间环境参数变化较小[31-32]，本文通过数据序列中相邻节点间的归一化偏差描述数据序列的稳定性。以环境温湿度数据为例，其时间序列相邻数据的归一化偏差占比如图3所示，从图中可以看出，环境温度序列的相邻节点归一化偏差小于0.02的占比超过60%，归一化偏小于0.04的占比超过90%；对于环境湿度序列，相邻节点归一化偏差小于0.02的占比超过95%，由此可以看出农业环境数据序列具有较高的稳定性。

基于农业环境数据的数据序列稳定性特征，本文采用(011)矩阵作为时域稳定性约束，时间约束矩阵捕获时间稳定性特征，限定了2个连续时隙之间的变化在一小范围内。时间约束矩阵定义如下。

空间约束矩阵捕获空间相似性特征，它表征了网络中一跳邻居节点之间值的关联约束。*为行归一化的得到，定义为

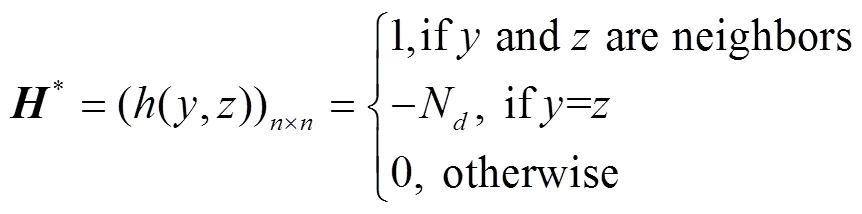
式中N为或的领居节点数量。

将农业物联网时间与空间约束矩阵代入式（12）可得

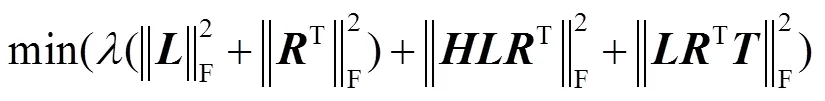
式中为约束均衡系数。

将式（15）、（11）代入式（10），则可得到基于农业环境时空约束的正则化回归KNN方法。

3 试验及结果分析

本文在MATLAB环境下对算法的性能进行验证，选取某温室的环境数据作为数据建模样本，采用交叉验证方法，其中训练集与测试集之比为4:1。对测试集数据采用数据丢失模型处理后作为重构算法的观测数据矩阵，利用不同算法从矩阵中恢复得出。对于回归的评价指标本文选用文献[2]中重构误差率（error ratio，ER），定义如下[2]

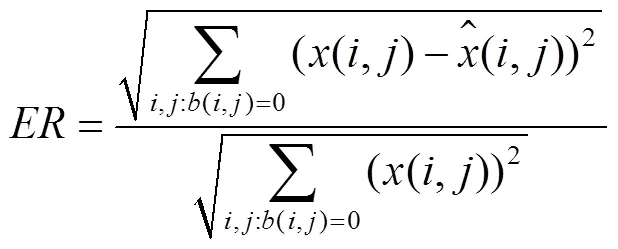
其中()=0表示只考虑数据丢失条件下的重构误差。

因农业物联网中节点碰撞、网络拥塞等问题多发，易出现短时间内的高数据丢失率现象，为充分体现高丢失率部分的性能变化趋势，验证中数据丢失率取值范围取10%～90%。

3.1 单点随机丢失模型重构试验

在单点随机丢失模型情形下，通过改变丢失数据的比例得出不同算法对该模型下的数据重构结果，如图4所示。其中图4a是农业环境温度数据重构结果，当数据丢失率为10%时4种算法的重构误差率均很小，约在1%以内，随着数据丢失率的提高，数据重构的误差率也随之升高，其中KNN的误差曲线上升最快，KNN-inverse次之，KNN-RP的误差曲线上升最慢。当数据丢失率增加至40%～50%左右时，不同算法的重构误差有了较明显的区别，后续随数据丢失率的增加，不同算法间性能进一步扩大，90%数据丢失率时，重构误差率为KNN约70%，KNN-inverse约55%，DT约35%，KNN-RP约20%。图4b是农业环境湿度数据重构结果，总体趋势与图4a类似，与之不同之处在于在低数据丢失率时重构误差率较环境温度的偏高，而高数据误差率时则与环境温度的结果相仿。环境湿度90%数据丢失率时重构误差为KNN约80%，KNN-inverse约50%，DT约35%，KNN-RP约18%。DT算法在数据丢失率50%～60%附近出现了重构误差率的明显提升，而在60%以上重构误差增加反而较为平缓。图4c是农业环境光照数据重构结果，由于光照数据在夜间有较长时段为0值，为客观体现算法重构性能，在构建环境光照数据集时将夜间连续为0值的数据删除。如图4c所示，4种算法从低数据丢失率（10%）时的重构误差已有较明显区别，10%数据丢失率时，重构误差率为KNN约5%，KNN-inverse约14%，DT约8%，KNN-RP约2%，随着数据丢失率的升高，KNN的重构误差率迅速升高，而其他3种算法的重构误差率则上升较缓，甚至DT与KNN-RP算法在数据丢失率60%～70%附近还出现了重构误差的略微下降。环境光照数据90%丢失率时重构误差为KNN约80%，KNN-inverse约50%，DT约35%，KNN-RP约20%。

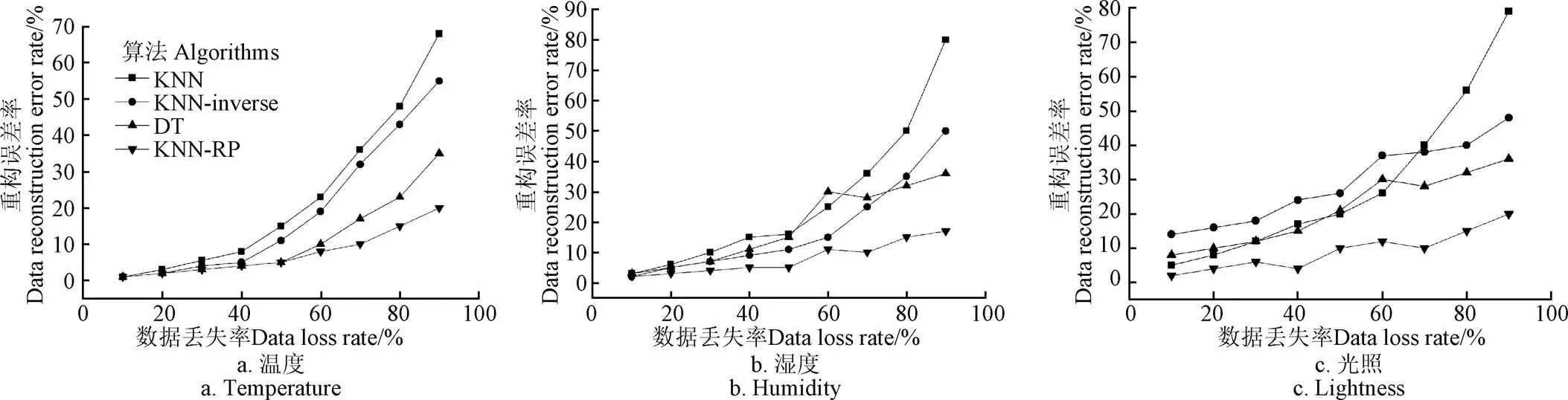
图4 单点随机丢失模型下不同算法的重构误差对比

总体上看在单点随机丢失模型下，随着数据丢失率的提高，不同算法的数据重构误差也随之升高；在高数据丢失率部分KNN的性能最差，KNN-RP的性能最好。但在低数据丢失率部分，不同算法在不同环境参数下的重构性能有一定区别。分析其可能原因是，对于曲线较为平滑的环境参数采用最邻近方法的回归性能较好，而对于局部变化频繁的环境参数则最邻近方法会增加不确定性。

3.2 块随机丢失模型重构试验

按照3.1中同样方法对块随机丢失模型情形进行仿真，由于丢失块的长度与位置是随机的，则改变整体数据丢失率对不同算法在块随机丢失模型下的重构性能进行对比，如图5所示。其中图5a是环境温度数据重构结果，当数据丢失率为10%时4种算法的重构误差率均小于10%，随着数据丢失率的提高，数据重构的误差也随之升高，其中KNN的误差率上升最快，KNN-inverse次之，DT算法的误差率上升最慢。当数据丢失率增加到90%时，不同算法的重构误差率为，KNN约90%，KNN-inverse和KNN-RP相当，约为70%，DT约60%，KNN-RP约20%。图5b是环境湿度数据重构结果，4种算法在重构误差率均随数据丢失率的增加单调递增，环境湿度数据丢失率为10%时，KNN-inverse和KNN-RP算法的重构误差率约为10%，而KNN和DT算法的重构误差率均小于10%；环境湿度数据90%丢失率时重构误差率分别为，KNN约90%，KNN-inverse约72%，DT约58%，KNN-RP约61%。整体上看，对于块随机丢失模型下的环境湿度数据而言，KNN的重构误差率最高，KNN-inverse次之，KNN-RP与DT算法性能相当，KNN-RP重构误差率略高于DT算法。图5c是环境光照数据重构结果，对于光照数据0值处理方式同3.1节单点丢失模型，光照数据丢失率10%时，重构误差率最高的KNN-inverse接近20%，其次是DT算法约10%，再是KNN约5%，KNN-RP略低于KNN；随着数据丢失率的升高，KNN与KNN-RP的重构误差率呈明显单调递增趋势，KNN-inverse的重构误差率呈阶梯状变化，DT算法在丢失率大于50%后重构误差率出现波动变化，光照数据90%丢失率时重构误差为KNN约78%，KNN-inverse约47%，DT约36%，KNN-RP约60%。整体上，对于同样的数据丢失率情形，块丢失的数据重构性能要低于单点随机丢失情形，由于KNN及其改进算法较为依赖关联度最高的节点信息，而块丢失会导致最高关联数据点缺失的比例提高。而DT算法在块随机丢失场景下表现的性能要优于其他3种算法。从算法复杂度的角度而言，KNN算法的时间复杂度为()[3,5,8]，KNN-inverse只是改变了KNN算法的距离计算方法，时间复杂度也为()，DT算法通过增量计算提高精度，其时间复杂度也随之提高为(lg)[2-5]，对于KNN-RP算法而言，由于式（10）中存在矩阵相乘、求逆运算，所以其算法复杂度应为(3)。

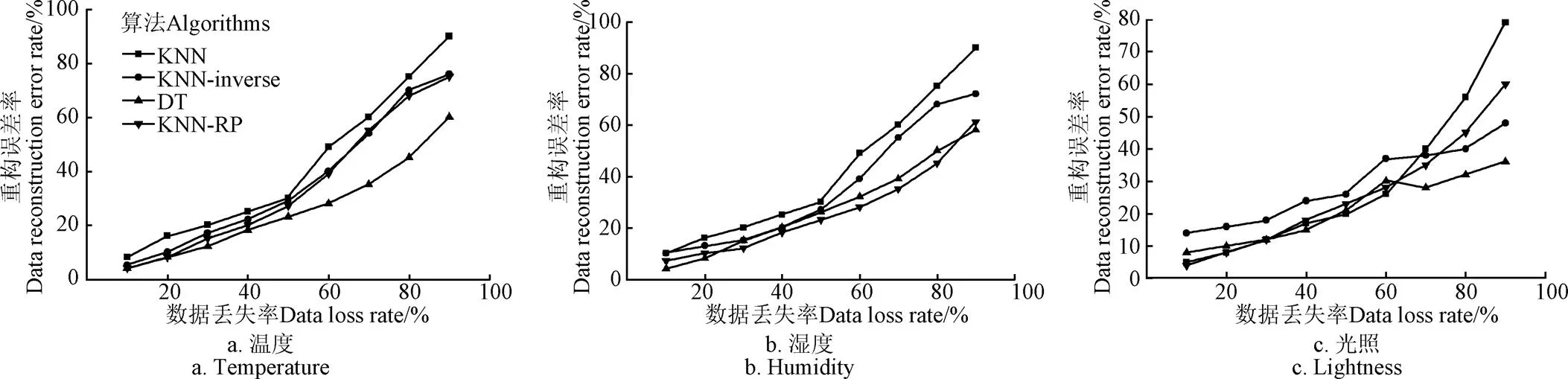
图5 块随机丢失模型下不同算法的重构误差对比

3.3 不同K值重构性能对比

为进一步分析值选择对于算法重构性能的影响，本文以KNN-RP算法在单点随机丢失模型下数据丢失率为40%情形下为例，通过改变值对比数据重构的误差。如图6所示，KNN-RP算法的重构误差随值的增大呈现先减小后增大的趋势。

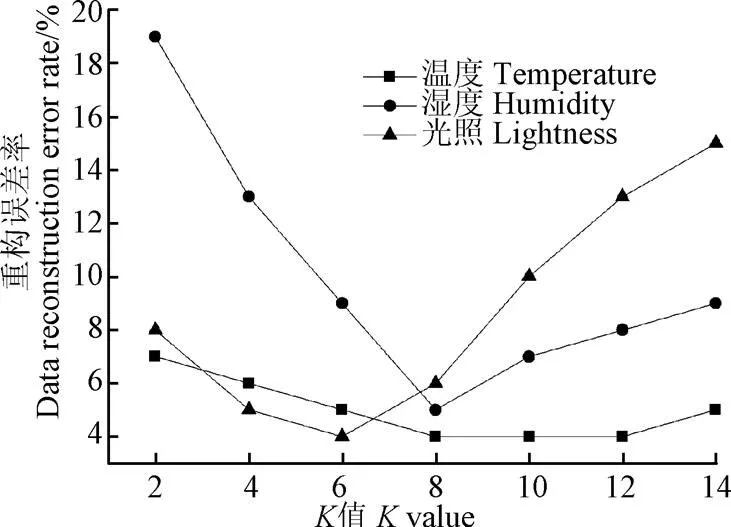
图6 单点随机丢失模型40%数据丢失率时K值对KNN-RP算法重构误差的影响

对于环境温度数据，重构误差总体随值变化较小，在取2时算法重构误差约为7%，重构误差随值增大而下降，当取8时误差降到最低约4%，随后重构误差随值增大而逐渐增大，当取14时误差增大为约5%。对于环境湿度数据，在取2时算法重构误差约为19%，重构误差随值增大而下降，当取8时误差降到最低约6%，随后重构误差随值增大基本稳定，略有增加。对于环境光照数据，在取2时算法重构误差约为8%，重构误差随值增大而下降，当取6时误差降到最低约4%，随后重构误差随值增大而迅速增大，当取14时误差增大为约15%。从结果中可以看出，的取值对于KNN-RP算法有显著影响，对于数据变化较稳定的环境温度而言，重构误差受值的影响相对较小，而对于变化较明显的环境湿度与光照数据而言，重构误差受值的影响相对较大，总体上对于温度、湿度和光照3种环境参数而言，最优的值在6～8之间。

4 结论与讨论

本文提出一种基于正则化惩罚的KNN重构方法，利用农业物联网数据的时空稳定性与相关性等特点建立关联约束对损失函数进行修正。通过对农业物联网监测数据在不同数据丢失模型下的进行了重构测试。试验结果证明，本文方法对于单点随机丢失模型的重构性能较好，而对于块随机丢失模型高数据丢失率情形其重构性能低于DT算法，整体上本文方法具有较高的准确性和稳定性，实现了农业复杂环境下物联网异常数据的有效重构，提高了数据质量与可信度。

对于块丢失模型中丢失率60%以上时KNN-RP重构性能不佳的问题，后续考虑结合长短期记忆模型，保证数据间关联约束的稳定。而且，本文中对于异常数据仅考虑了数据缺失与错误的类型，并未将数据噪声纳入分析，后续考虑引入数据噪声使得结果更加接近于实际数据环境，此外考虑通过矩阵降维等方式降低KNN-RP算法的时间复杂度也是后续需要研究解决的问题之一。

[1] Jesus G, Casimiro A, Oliveira A. A survey on data quality for dependable monitoring in wireless sensor networks[J]. Sensors, 2017, 17(9): 2010.

[2] Kong L, Xia M, Liu X Y, et al. Data loss and reconstruction in wireless sensor networks[J]. IEEE Transactions on Parallel & Distributed Systems, 2014, 25(11): 2818－2828.

[3] 段青玲，肖晓琰，刘怡然，等.基于改进型支持度函数的畜禽养殖物联网数据融合方法[J]. 农业工程学报，2017，33(增刊1)：239－245.

Duan Qingling, Xiao Xiaoyan, Liu Yiran, et al. Data fusion method of livestock and poultry breeding internet of things based on improved support function[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Supp.1): 239－245. (in Chinese with English abstract)

[4] Chen S, Zhao C, Wu M, et al. Compressive network coding for wireless sensor networks: Spatio-temporal coding and optimization design[J]. Computer Networks, 2016, 108: 345－356.

[5] Sun J, Yu Y, Wen J. Compressed-sensing reconstruction based on block sparse bayesian learning in bearing- condition monitoring[J]. Sensors, 2017, 17(6): 1454.

[6] Wu H, Suo M, Wang J, et al. A holistic approach to reconstruct data in ocean sensor network using compression sensing[J]. IEEE Access, 2018, 6(99): 280－286.

[7] Jayawardhana M, Zhu X, Liyanapathirana R, et al. Compressive sensing for efficient health monitoring and effective damage detection of structures[J]. Mechanical Systems & Signal Processing, 2017, 84: 414－430.

[8] 潘立强，李建中，骆吉洲. 传感器网络中一种基于时-空相关性的缺失值估计算法[J]. 计算机学报，2010，33(1)：1－11.

Pan Liqiang, Li Jianzhong, Luo Jizhou. A temporaland spatial correlation based missing values imputational gorithm in wireless sensor networks[J]. Chinese Journal of Computers, 2010, 33(1): 1－11. (in Chinese with English abstract)

[9] Eldar Y C, Kuppinger P, Bolcskei H. Block-sparse signals: uncertainty relations and efficient recovery[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3042－3054.

[10] Morell A, Correa A, Barceló M, et al. Data aggregation and principal component analysis in WSNs[J]. IEEE Transactions on Wireless Communications, 2016, 15(6): 3908－3919.

[11] Ghazanfari-Rad S, Labeau F. Formulation and analysis of lms adaptive networks for distributed estimation in the presence of transmission errors[J]. IEEE Internet of Things Journal, 2017, 3(2): 146－160.

[12] Tan L, Wu M. Data reduction in wireless sensor networks: A hierarchical LMS prediction approach[J]. IEEE Sensors Journal, 2016, 16(6): 1708－1715.

[13] Argyriou A, Özgü Alay. Distributed estimation in wireless sensor networks with an interference canceling fusion center[J]. IEEE Transactions on Wireless Communications, 2016, 15(3): 2205－2214.

[14] Wu M, Tan L, Xiong N. Data Prediction, Compression, and Recovery in Clustered Wireless Sensor Networks for Environmental Monitoring Applications[M]. New York: Elsevier Science Inc. 2016.

[15] Miranda K, Ramos V. Improving data aggregation in wireless sensor networks with time series estimation[J]. IEEE Latin America Transactions, 2016, 14(5): 2425－2432.

[16] 江冰，毛天，唐大卫，等.基于农田无线传感网络的分簇路由算法[J]. 农业工程学报，2017，33(16):182－187.

Jiang Bing, Mao Tian, Tang Dawei, et al. Clustering routing algorithm based on farmland wireless sensor network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(16): 182－187. (in Chinese with English abstract)

[17] Xu X. Data Approximation for time series data in wireless sensor networks[J]. International Journal of Data Warehousing and Mining, 2016, 12(3): 1－13.

[18] Morell A, Correa A, Barceló M, et al. Data aggregation and principal component analysis in WSNs[J]. IEEE Transactions on Wireless Communications, 2016, 15(6): 3908－3919.

[19] Panigrahi T, Panda M, Panda G. Fault tolerant distributed estimation in wireless sensor networks[J]. Journal of Network & Computer Applications, 2016, 69(C): 27－39.

[20] Li X, Tao X, Mao G. Unbalanced expander based compressive data gathering in clustered wireless sensor networks[J]. IEEE Access, 2017, 5(99): 7553－7566.

[21] Yan W, Dong Y, Zhang S, et al. An optimal CDG framework for energy efficient WSNs[J]. Chinese Journal of Electronics, 2017, 26(1): 137－144.

[22] Klis R, Chatzi E N. Vibration monitoring via spectro-temporal compressive sensing for wireless sensor networks[J]. Structure & Infrastructure Engineering, 2016, 13(1): 195－209.

[23] Chen X, Yin X, Yu B, et al. Communication channel reconstruction for transmission line differential protection: System arrangement and routing protocol[J]. Energies, 2016, 9(12): 893.

[24] Wang T Y, Yang M H, Wu J Y. Distributed detection of dynamic event regions in sensor networks with a gibbs field distribution and gaussian corrupted measurements[J]. IEEE Transactions on Communications, 2016, 64(9): 3932－3945.

[25] Zhu X F, Huang Z, Yang Y, et al. Self-tau-ght dimensionality reduction on the high-dimensional small-sized data[J]. Pattern Recognition, 2013, 46(1): 215－229.

[26] 龚永红，宗鸣，朱永华，等. 基于混合模重构的kNN回归[J]. 计算机应用与软件，2016(2)：232－236.

Gong Yonghong, Zong Ming, Zhu Yonghua, et al. Knn regression based on mixed-norm reconstruction[J]. Computer Applications & Software, 2016(2): 232－236. (in Chinese with English abstract)

[27] Geeta D D, Nalini N, Biradar R C. Fault tolerance in wireless sensor network using hand-off and dynamic power adjustment approach[J]. Journal of Network & Computer Applications, 2013, 36(4): 1174－1185.

[28] Qaisar S, Bilal R M, Iqbal W, et al. Compressive sensing: From theory to applications, a survey[J]. Journal of Communications & Networks, 2013, 15(5): 443－456.

[29] Park H, Kim B S, Kim K H, et al. A tree based broadcast scheme for (m,k)-firm real-time stream in wireless sensor networks[J]. Sensors, 2017, 17(11): 2578.

[30] Park J, Bok K, Seong D, et al. A data gathering method based on a mobile sink for minimizing the data loss in wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2014, 2014(5): 242.

[31] Nguyen N T, Pham V T, Pham V T, et al. On maximizing the lifetime for data aggregation in wireless sensor networks using virtual data aggregation trees[J]. Computer Networks the International Journal of Computer & Telecommunications Networking, 2016, 105(C): 99－110.

[32] Zhu L, Huang Z, Liu Y, et al. The Nonparametric Bayesian dictionary learning based interpolation method for WSNs missing data[J]. AEU-International Journal of Electronics and Communications, 2017, 79: 267－274.

Agricultural internet of things data reconstruction based on K-nearest neighbor reconstruction algorithm improved by regularization penalty and spatio-temporal constraints

Wu Huarui1,2, Li Qingxue1,2,Miao Yisheng1,2, Song Yuling3

(1.100097; 2.100097; 3.712100,)

The internet of things (IoT) technology has been widely applied in the agriculture production monitoring. Accurate decision-making and environment regulation can be made based on monitoring results. However, data loss in agriculture wireless sensor networks is common due to noise, collision, unreliable link, and unexpected damage, which greatly reduces the quality of data acquisition and then affects the results of decision analysis. In order to solve this problem, this paper proposed a data reconstruction method based on K nearest neighbor with regularization penalty constraints (KNN-RP). Firstly, the ridge regression method was used in order to regularize the least square factor. Secondly, there was a problem that it is difficult to get a unique solution due to the algorithmic error while the data matrix is not full-column rank. This could be improved by introducing a penalty term into the method. The combination of 1-norm and 2-norm could ensure the sparsity of the matrix as well as prevent the loss function from over-fitting. It is suitable for high-dimensional agricultural WSN (wireless sensor network) data reconstruction with high noise. Furthermore, the definition of time and space constraint matrix was determined according to the temporal and spatial stability of perceptual data in agricultural IoT. Finally, thevalue was determined by model training to achieve the better reconstruction performance. A cross-validate experiment was done to evaluate the algorithm performance according to the greenhouse data samples. KNN (K nearest neighbor), KNN-inverse and DT (delaunay triangulation) algorithms were chosen for the performance comparison. In the element random loss case, the overall reconstruction error rate of the 4 algorithms increased with the increasing of data loss rate. The KNN and KNN-inverse had higher error rate when the data loss rate above 60% compared with the other 2 algorithms. Besides, the performance of KNN-RP was superior to the DT algorithm in both high and low data loss rates. In the block loss case, the reconstruction error rates of the 4 algorithms were close to the element random loss case, but reconstruction error rates increased faster than the element random loss case while the data loss rate increased. In the block loss case, the overall performance of KNN-RP was better than KNN and KNN-inverse, but lower than that of DT algorithm when the data loss rate was above 60%. Thevalue had a significant influence on the performance of KNN-RP. The reconstruction error of KNN-RP decreased first and then increased with the increasing ofvalue. For the stable parameter like temperature, the reconstruction error rate was less affected byvalue. On the contrast, the reconstruction error rates of humidity and lightness data were more affected byvalue. The reason maybe the humidity and lightness data changed faster than temperature. Considering all 3 parameters, temperature, humidity and lightness, the optimalvalue was between 6 and 8. In summary, KNN-RP algorithm could effectively reconstruct the missing errors in the agricultural IoT, especially in element random loss case. The proposed algorithm improves the quality of perceptual data in agricultural IoT monitoring and may provide reference for agricultural production decision-making.

algorithms; models; agricultural internet of things; data reconfiguration; cluster regression

2018-11-29

2019-06-20

国家自然科学基金项目（61871041, 61571051）；北京市自然科学基金项目（4172024, 4172026）；农业农村部农业物联网重点实验室开放课题（2018AIOT-06）

吴华瑞，研究员，主要从事农业智能系统与物联网研究。Email：wuhr@nercita.org.cn

李庆学，助理研究员，主要从事农业物联网与智能系统研究。Email：liqx@nercita.org.cn

10.11975/j.issn.1002-6819.2019.14.023

TN919

A

1002-6819(2019)-14-0183-07

吴华瑞，李庆学，缪祎晟，宋玉玲.基于正则化与时空约束改进K最近邻算法的农业物联网数据重构[J]. 农业工程学报，2019，35(14)：183－189. doi：10.11975/j.issn.1002-6819.2019.14.023 http://www.tcsae.org

Wu Huarui, Li Qingxue, Miao Yisheng, Song Yuling. Agricultural internet of things data reconstruction based on K-nearest neighbor reconstruction algorithm improved by regularization penalty and spatio-temporal constraints[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(14): 183－189. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.14.023 http://www.tcsae.org