螺杆压缩机接触线形状及长度的计算方法

蔡 宏，杨 威

（1.西漠能源技术（苏州）有限公司，江苏苏州215500；2.西安航天动力测控技术研究所，陕西西安710000）

1 引言

螺杆压缩机是一种回转容积式压缩机，由于可靠性高、操作维护方便、动力平衡性好，在空气动力、制冷低温及石油化工领域得到了广泛应用。螺杆压缩机转子齿面相互接触形成的空间曲线称为接触线，其形状及长度对螺杆压缩机性能有重大影响。接触线的计算关键在于型线坐标参数与压缩机转角的关系，常规计算方法由隐函数获得[1]。由于隐函数的求解较为困难，求取接触线长度通常需要离散接触线各点空间坐标，再叠加这些点的距离获得[2]。上述计算方法在已知螺杆压缩机齿型的条件下较为适用，如用于新型线设计及参与压缩机数模模拟工作量较大。本文基于空间曲线的啮合定律，用显函数型式给出了型线坐标参数与压缩机转角的关系，简化了接触线形状与长度的计算。

2 空间曲线的啮合定律

螺杆压缩机的转子是由具有一定形状的曲面组成，该曲面被垂直转子轴线的端平面截得一平面曲线。

一条平面曲线的直角坐标参数方程用下式表示

该曲线的坐标x和y都是参数t的函数，而参数t的起点ta和终点tb就决定了此曲线的起点a和终点b的坐标（xa，ya）、（xb，yb）。

如转子的转子齿形的参数方程用式（1） 表示，让转子齿形以导程p绕转子轴线作右旋运动，轴向前进距离是z，相对原始位置转过角度τ，那么相应的螺旋面方程可以表示为[3]

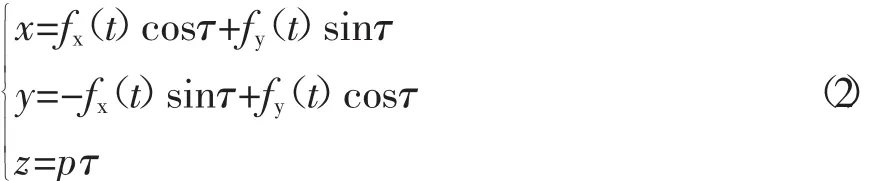
螺杆压缩机的啮合属于平行轴啮合，图1为啮合示意图，阳转子曲线段1-1与阴转子曲线段2-2以速度v在点M啮合，n为啮合点的公法线，节点p是瞬时回转中心。由啮合条件，n既要与Mp在一个平面，又要与v在一个平面，只有n与Mp重合，即两共轭曲线啮合点的公法线必定通过节点，这就是啮合的基本定律。

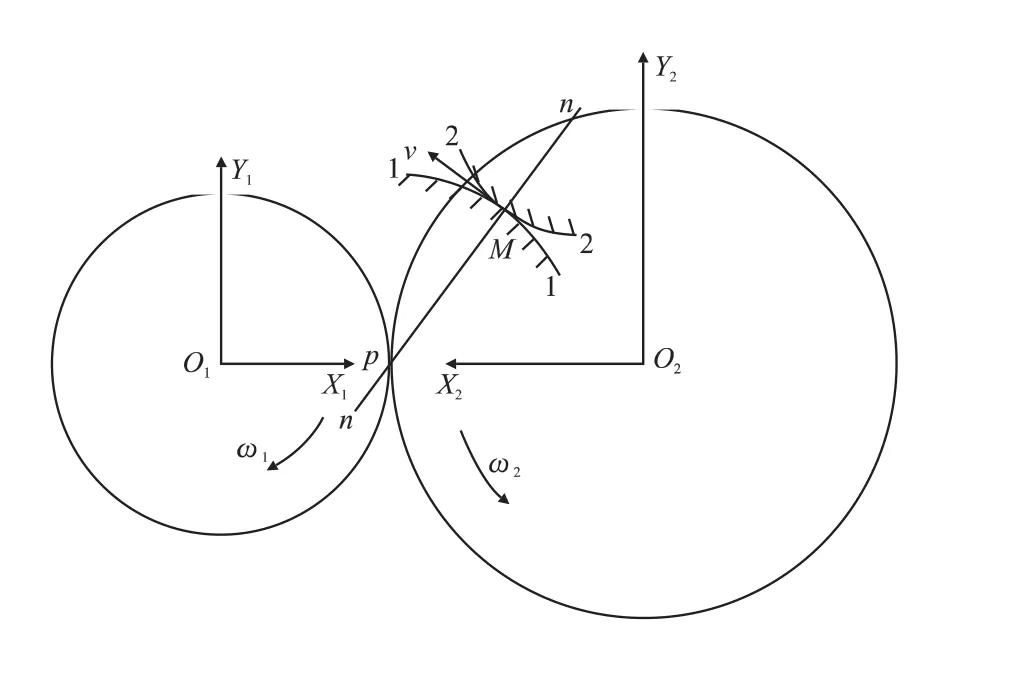
图1 啮合示意图

3 接触线方程

螺杆压缩机的阴、阳转子啮合时，两转子齿面相互接触而形成的空间曲线称为接触线。接触线在端平面上的投影称为啮合线。引入端面齿形及其啮合线就使空间的曲面、曲线转为平面问题。

图2为求解接触线啮合条件式的示意图。r1t，r2t为节圆半径，i为传动比，i=r1t/r2t。

如阳转子上点M1坐标为（x1，y1），x1，y1均为参数t的方程，啮合点M的坐标参数为

根据啮合基本定律

联立式（3） 与式（4），解得τ与t的函数关系。

将式（5） 代入式（3），即可获得啮合点M的坐标参数。

如已知阴转子上点M2坐标为（x2，y2），x2，y2均为参数t的方程，则啮合点M的坐标参数为

其中τ与t的函数关系由啮合基本定律求取见式（7）。

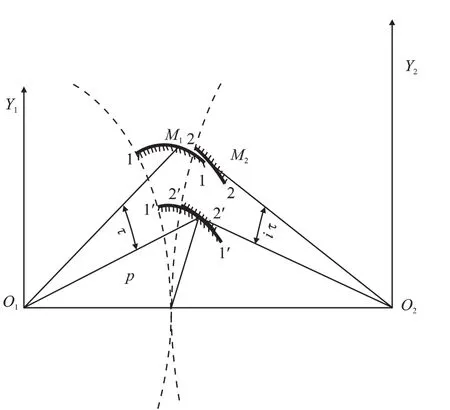
图2 接触线啮合条件式求解示意图

将式（7） 代入式（6），即可获得啮合点M的坐标参数。

4 接触线长度

如接触线起始点a坐标与b对应的型线参数与转角分别为（ta，τa）与（tb，τb），该段接触线在啮合过程中的长度计算方法由式（8）给出。

5 计算实例

根据式（3） ～（8） 给出的一系列关于接触线形状与长度的计算方法，下面针对典型的螺杆压缩机型线——SRM型线，对接触线形状与接触线长度进行求解。其中接触线形状示意图见图3，齿间容积接触线长度见图4。

图3 接触线形状示意图

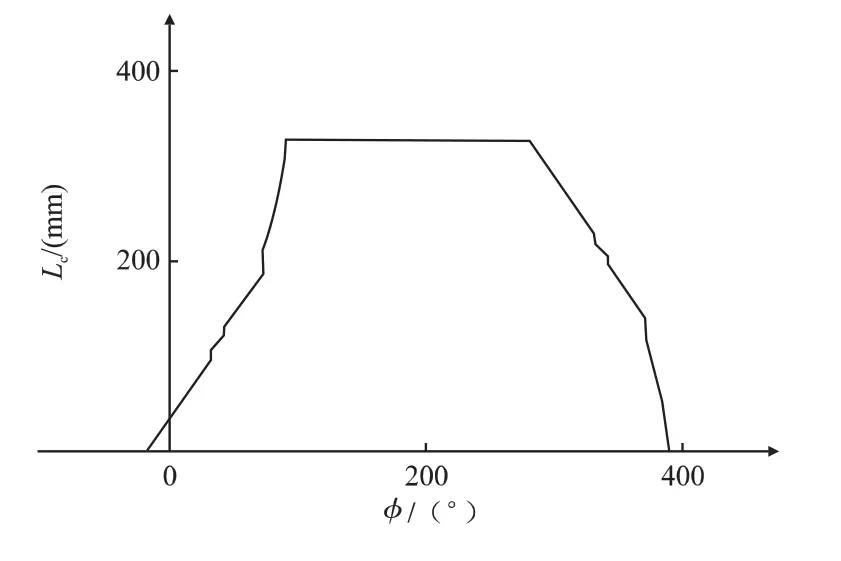
图4 接触线长度示意图

6 结论

鉴于接触线的几何特性对螺杆压缩机的性能至关重要，如能以较简便的方法获得接触线的形状及长度，将大大简化型线设计及数模模拟过程。本文基于空间曲线的啮合定律，计算了螺杆压缩机接触线的形状与长度，由于该计算方法基于解析法，因此适合采用计算机进行编程运算，且可嵌入后续的螺杆压缩机热力学与动力学计算，可有效提高螺杆压缩机数值模拟的效率与准确度。