基于小脑内模机理的自平衡机器人平衡控制

陈 静

（天津职业技术师范大学信息技术工程学院，天津 300222）

由于医学的迅速发展，脑的结构方面的研究已经相当成熟，脑的行为包括：思考、感觉、听觉、语言、运动、触觉、视觉、平衡等，脑就是高级神经中枢所在地，控制人的这些行为。其中小脑部位主要是控制人体的平衡，而两轮自平衡机器人具有拟人的特点，需要有平衡控制器去负责系统的平衡，模拟小脑的控制机理对于构建自平衡机器人的控制系统是有效的。

20 世纪60 年代，神经生理学的诸多研究学者（Brindley 等）提出了如果平行纤维（parallel fiber）和浦肯野细胞（Purkinje cell）之间的神经键连接是可修改的，那么就可以形成记忆。1968 年，Flourens 意识到了小脑的动力学功能，他指出小脑的功能就是协调运动。对于运动来说小脑不是必须的，但是没有小脑，肢体的运动就会出现急动、震颤、不牢固和不精确。Ito[1]将内模（internal model）的概念引入神经生理学，提出内模是学习或训练的产物，中枢神经系统（central nervous system，CNS）利用内模进行运动控制，并且提出了前向模型（forward model）假设。缺点：前向型内模反馈增益小，反馈延迟大，中枢神经组织难以完全依赖前向模型进行运动和控制，不利于运动控制的快速性和平稳性。1987 年，Kawato 等[2]提出逆向模型（inverse model），后又提出反馈误差学习模型[3]（feedback-error-learning model），期望轨迹和实际轨迹的差值作为前向模型的学习训练信号，同时解决了不同误差信息的归一化。根据Kawato 的观点，前向内部模型预测行为序列并且联合反馈控制能够被用来克服时间延迟。可以说，FEL 机制是为了建立中枢神经系统（CNS）中与运动神经学习和控制（motor learning and control）相关的小脑计算模型而提出的一种逆向模型，是一种“目标引导”的学习方法，是生物学领域比较合理的监督式运动学习机制。针对非线性平衡控制问题，2007 年，一种基于反馈误差学习（FEL）的在线自适应控制机制[4]被成功用于倒立摆的平衡控制，这一学习机制在一定程度上说明了小脑在保持身体平衡中所起的作用。研究人员在构造系统的自适应逆控制方法中也选择了反馈误差学习[5]，并将该方法用于电机的速度控制中[6]。近年来，有研究人员在非线性系统中将反馈误差学习方法构造扰动观测器[7]用于神经生理学领域。研究人员针对帕金森病的康复过程，进行了基于反馈误差学习的鲁棒自适应控制器设计的仿真研究[8]，为平衡系统的自适应性控制提供了参考，并且已有研究人员为自平衡机器人构建了模拟小脑功能的控制系统[9-11]。

鉴于反馈误差学习在感觉运动系统控制中的自适应优势，将其运用于自平衡机器人的自主学习控制中，成为一个较为合理的解决方案。本文用反馈误差学习构建自平衡车的平衡控制中枢，通过误差与反馈误差的比例参数进行自适应学习的参数调节，研究比例参数对学习性能的影响，并与反馈控制效果进行对比。

1 反馈误差学习结构

反馈误差学习机制的基本结构如图1所示。图中xd（t）为期望轨迹，是ufb（t）反馈控制器的输出；uff（t）为前馈神经网络自适应控制器的输出；u（t）= uff（t）+ufb（t）为作用于被控对象的控制量；x（t）为系统状态。学者已经证明反馈误差学习的收敛性。

2 机器人数学模型

自平衡机器人是典型的非线性欠驱动系统，常被研究人员用来验证算法性能[12-15]，本研究利用Lagrange方法建立了自平衡机器人的数学模型，该模型的系统状态（6 个变量）包括机器人倾角、左右轮角位移、倾角速度、左右轮角速度，均为可测的状态，向量定义为系统输入量有2 个，左右轮的输入转矩τl和τr，系统扰动有3 个，分别为上体受到的转矩扰动和左、右轮的转矩扰动。

为了便于分析该动力学模型并对机器人设计控制器，定义系统的状态变量为其中，则以转矩为控制量的系统非线性动力学方程为：

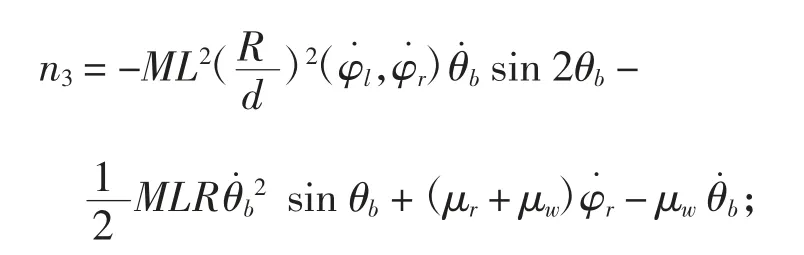
机器人模型参数如表1所示。

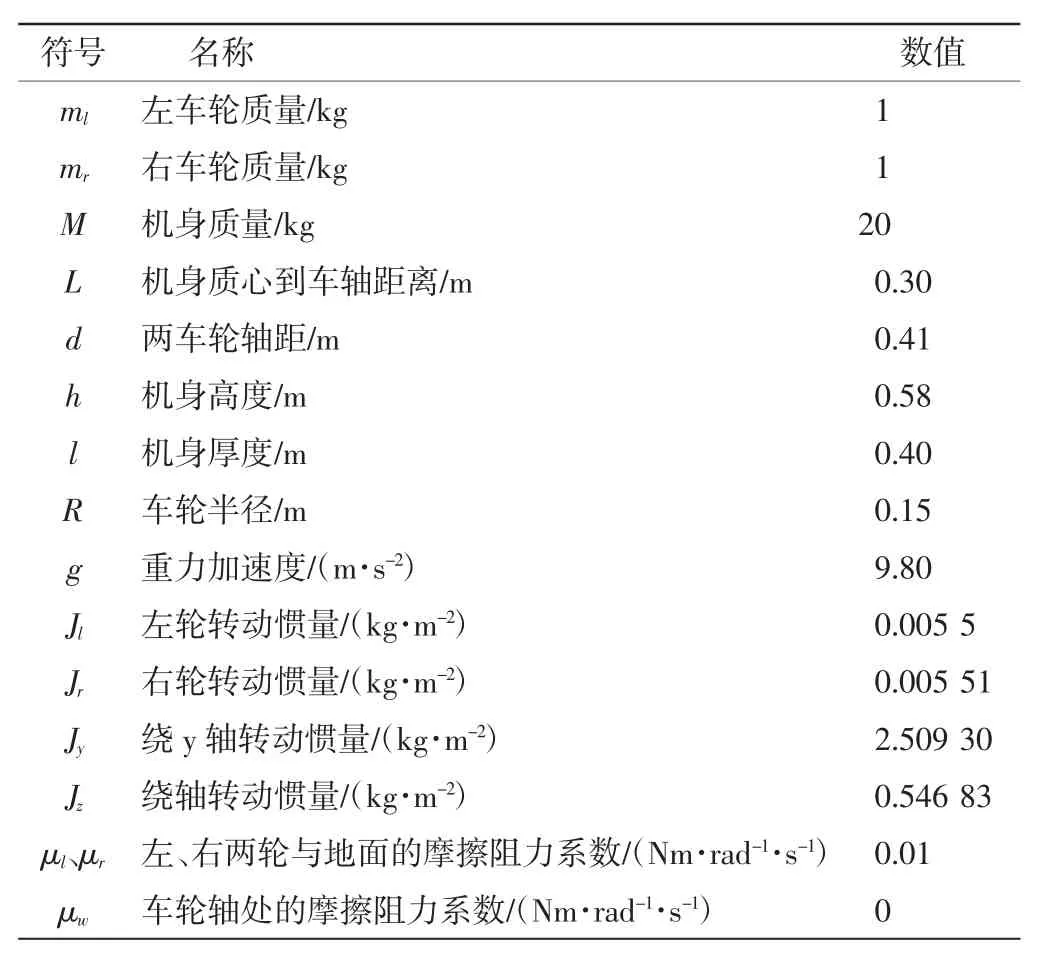
表1 机器人参数

3 基于改进反馈误差学习的小脑内模自适应控制

基于改进的反馈误差学习的小脑内模自适应控制结构如图2所示。

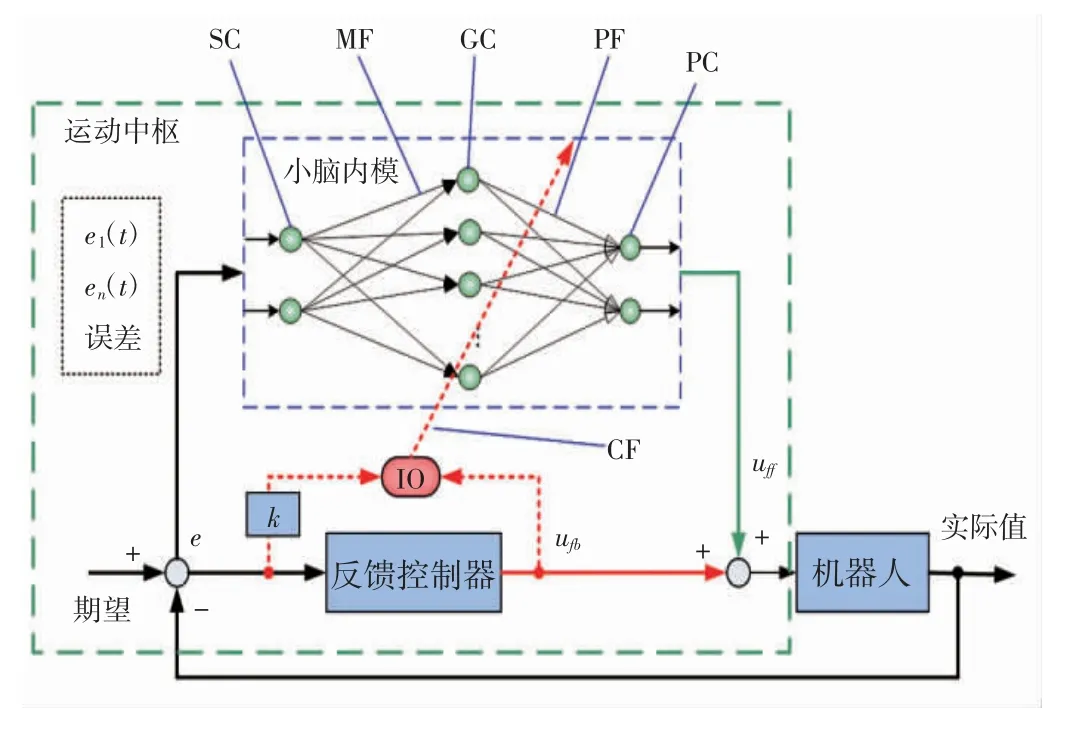
图2 小脑内模自适应控制结构

图中，小脑内模的输入神经元为感觉皮质（SC），隐含层神经元为颗粒细胞（GC），输出层神经元为普肯野细胞（PC），输入层到隐含层的连接权值通过苔状纤维（mossy fibers，MF）与GC 之间的突触进行修饰，隐含层和输出层的权值更新通过平行纤维（parallel fibers，PF）与普肯野细胞之间的突触进行修正。学习过程中通过下橄榄（inferior olive，IO）融合学习信号，实现小脑内模的自适应学习。

这里采用一个典型的单隐含层BP 网络（6-6-2结构，输入层6 个神经元，隐含层6 个神经元，输出层2 个神经元）作为小脑内模，如果用w 表示小脑内模的权值，则权值更新公式为：

式中：e=（xd-x）∈R6×1；uff∈R2×1；ufb∈R6×2；0＞η＞1 为小脑内模的学习率；0≤μ≤1；kT≥0。

计算过程中用到的神经网络运算公式为：

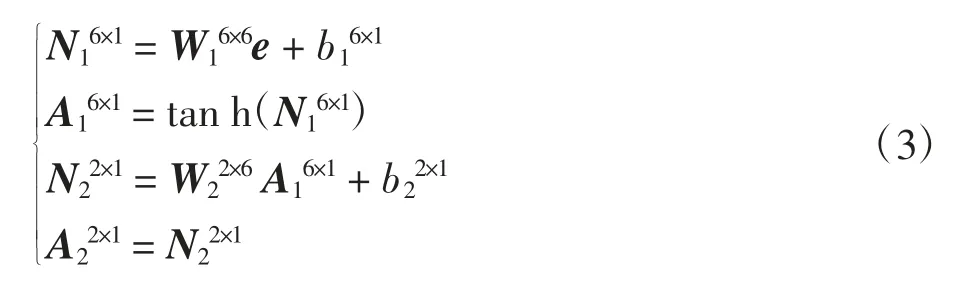
式中：N1为隐含层神经元输入信号；A1为隐含层神经元输出信号；N2为输出层神经元输入信号；A2为输出层神经元输出信号；W1为输入层神经元到隐含层神经元之间的连接权值；b1为隐含层神经元的偏置量；W2为隐含层神经元到输出层神经元之间的连接权值；b2为输出层神经元的偏置量。基于式（2）所示的各权值更新公式为：

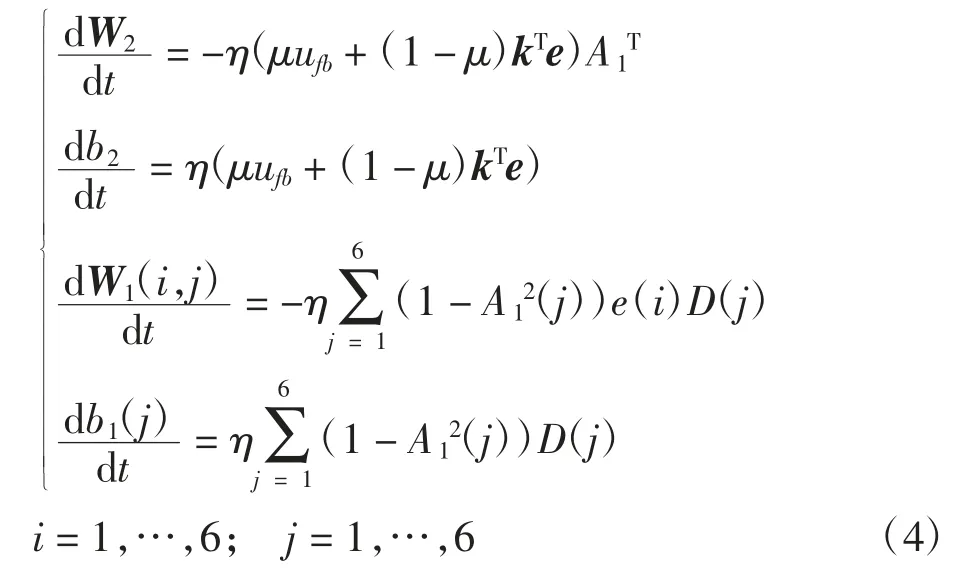
4 仿真研究

为了实现自平衡机器人的平衡控制，机器人的期望状态xd=[0；0；0；0；0；0]，机器人的初始倾角为9°，机器人的仿生控制结构如图3所示。

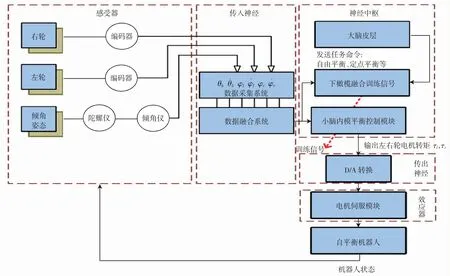
图3 机器人仿生控制结构

基于小脑内模的控制流程如下。

第一步：随机初始化神经网络的权值，初始化学习参数：μ=0.5（可调参数），η=0.5，k=[1，1，1，1，1，1；1，1，1，1，1，1]；第二步：不断采样误差e 和ufb值作为网络学习的数据；第三步：根据式（4）进行参数的更新；第四步：计算小脑内模的输出uff和ufb的和，作为机器人的控制输入，作用于机器人，使机器人状态发生更新。返回第二步，不断循环，一直到学习条件终止为止（如控制失败，或者平衡时间达到期望时间）。

在MATLAB2009a 软件中进行SIMULINK 仿真实验，仿真结果如图4-7所示。

仿真中所用的关键参数如下。

反馈控制器的增益矩阵为：

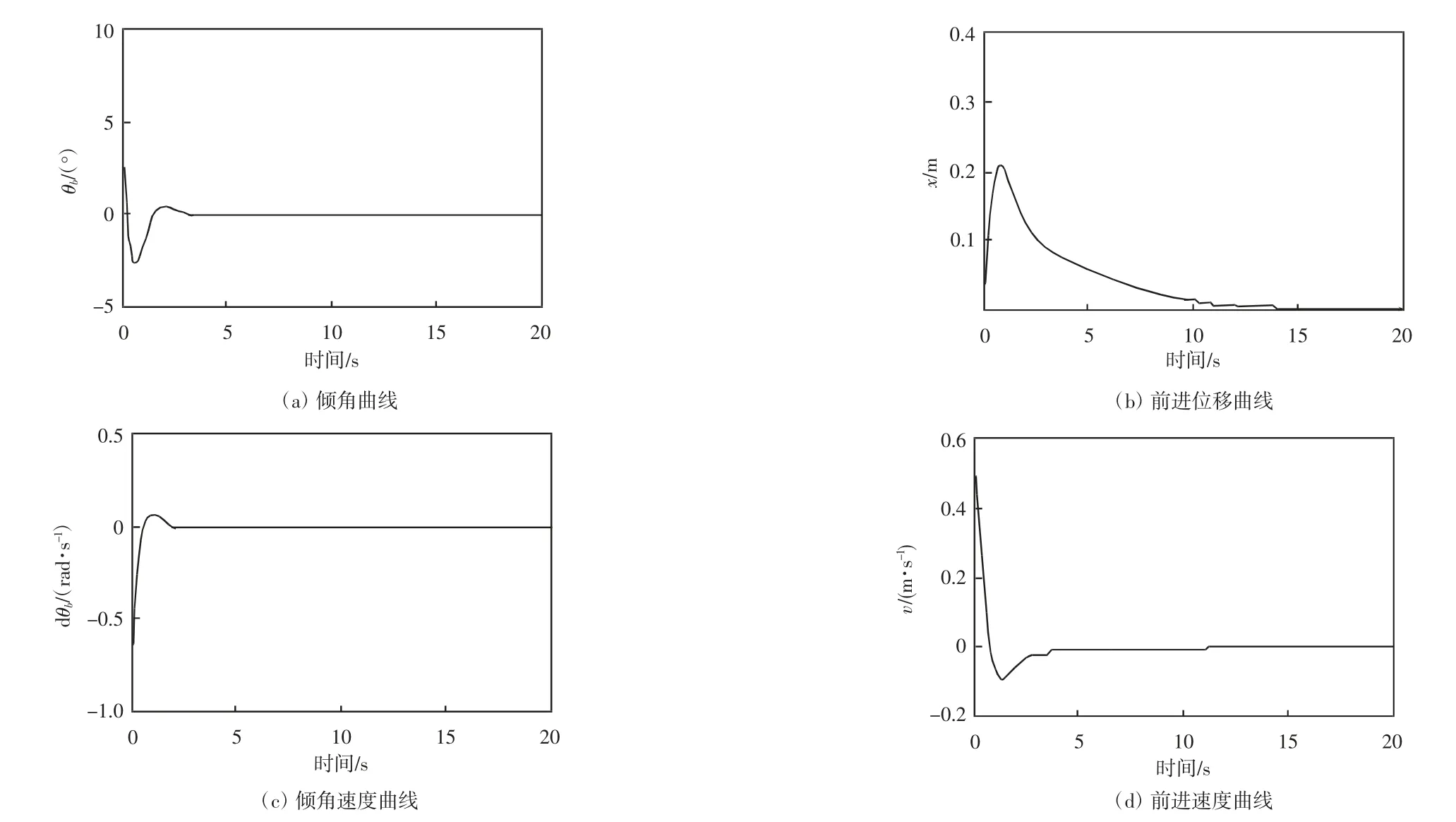
图4 μ=0.5 时机器人平衡效果

图5 对比结果1

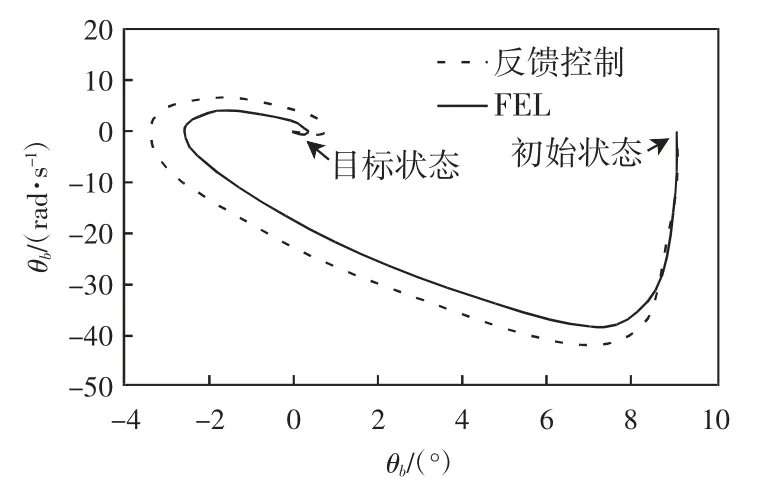
图6 对比结果2

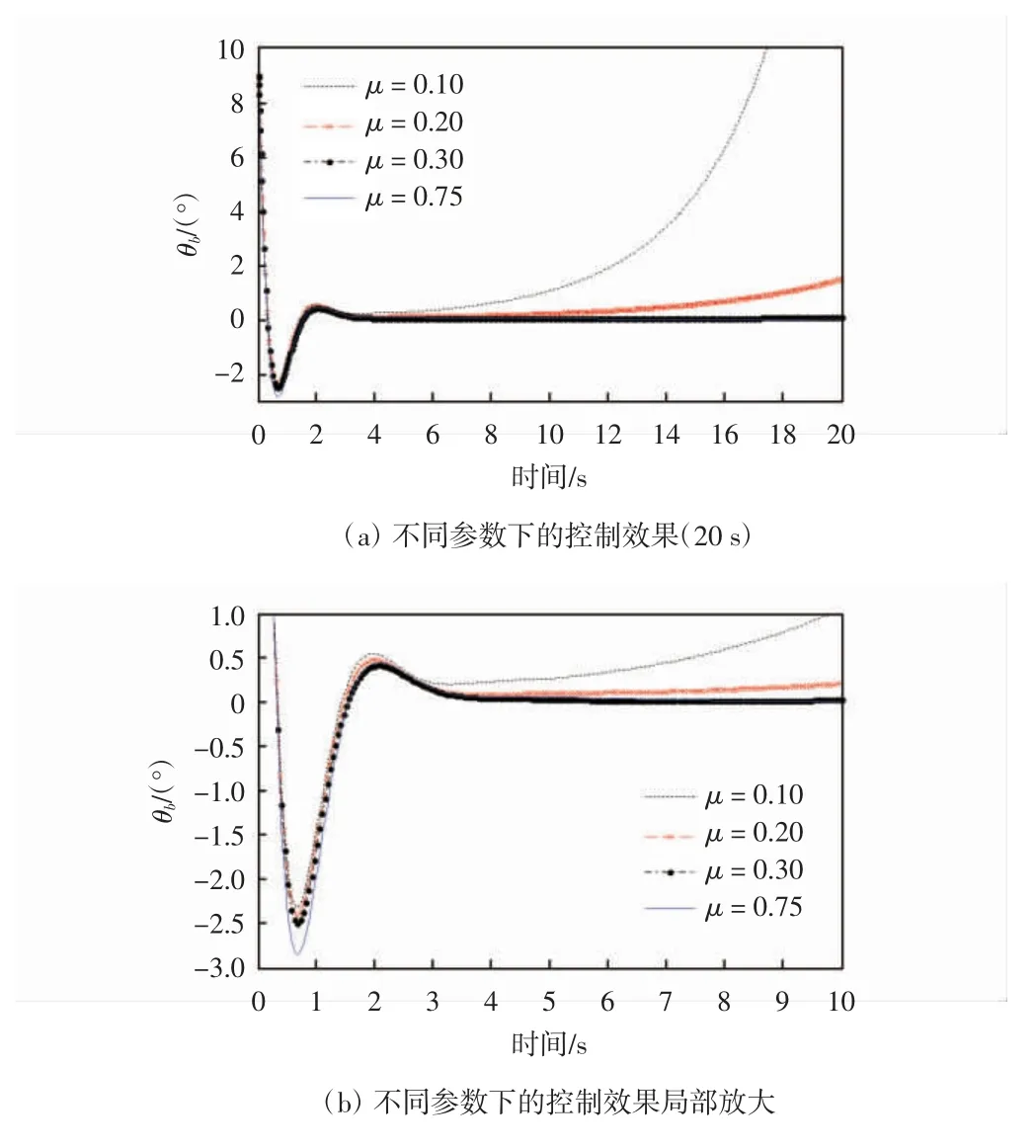
图7 不同参数μ下的控制效果对比

实验过程中，存储了μ 取值不同时的结果数据，并将倾角的控制效果进行了对比，当μ 取值较小时，平衡的初始时刻控制的倾角超调相对较小，但是运行的结束时刻会有发散现象，通过分析发现，μ 的较小取值，使得学习率取决于误差，而经过反馈增益矩阵的反馈误差作用较小，导致了控制效果不佳。通过增加μ 值，使得反馈误差起决定性作用时，控制效果达到理想状态，而且倾角的超调量并没有太大变化，但是控制的稳定性有所加强，从这个角度也可以看出反馈误差学习的优势。

5 结 语

本文提出了基于反馈误差学习的小脑内模自适应控制方法，用于自平衡机器人的平衡控制，比较了在不同参数下的控制效果，通过对比可以看出，反馈误差学习的自适应控制优势，通过与传统反馈控制方法的比较也可以看出基于反馈误差学习的小脑内模在自平衡机器人稳定平衡控制的优势较为明显，可以有效解决自平衡机器人的自适应稳定平衡控制。