基于充放电模型的电动汽车充电价格设定策略

聂 津，陈 涵，叶必超

（国网电动汽车服务（福建）有限公司，福州 350003）

0 引言

随着风、光、太阳能等新能源发展与电动汽车技术的日益成熟，电动汽车的发展也逐步加快，预计2020 年我国电动汽车保有量将达到500万辆。电动汽车的大规模增加，给智慧城市建设发展带来了巨大挑战，例如城市交通、充电需求以及电网冲击等[1]，利用充电价格可以引导电动汽车用户有序充电以减少其带来的负面影响。最新的双向充放电技术使得电网运营方可借助电动汽车电池作为V2G（移动储能），调整充电价格调度电动汽车充电行为使其为电网所用[2]。

如何制定充电价格策略以达到电网运营与用户充电成本之间的平衡是目前的研究热点。首先是基于数据驱动的区域负荷与充电负荷的预测工作，Mostafa Majidpour 和Qiu Charlie 等人利用KNN（邻近算法）、时间权重序列预测等方法估计用户充电负荷，分析了洛杉矶的充电需求[3]；Emre C．kara 和Jason S．Macdonald 则基于数据挖掘策略，分析了非住宅区充电需求，并制定策略减少峰值负荷[4]。其次，Cao Yijia 和Tang Shengwei 提出了利用分时电价与电动汽车电池曲线制定充电模型，并利用启发式算法求解[5]；Fan Hao 和Hou Hui 等人在前人工作基础上，利用分时电价制定充放电策略以减少用户充电成本，并根据优化结果确定分时电价[6]；Jian Linni，Zhu Xinyu 和Shao Ziyun利用电动汽车电池作为移动储能，优化电网负荷波动情况[7]；葛少云注重电网运行中的峰谷差优化，利用峰谷电价，使用蒙特卡洛方法模拟负荷与遗传算法求解优化模型，得到电动汽车有序充放电策略[8]；Bai Xingzhen 在分时电价背景下，将用户充电成本、电动汽车充电捕捉与最小化电网负荷波动相结合，利用多目标优化与数据制定优化策略[9]。上述研究都仅关注于在某确定电价下如何制定最优充放电策略，而Hu Zechun，Zhan Kaiqiao 等人根据负荷波动以及用户成本制定了负荷电价机制，其电价主要关注于峰谷差功率调节[10]；Fan Bo 和Yang Qinmin 则关注配网中电网的瞬态电压控制，利用保性能控制方法设计控制器稳定电网[11]。

已有的研究对电网自身特性与其充电价格设定以及与电动汽车的交互研究较为薄弱，重点关注的是获取充电汽车的用户数据，利用数据设置分时电价以调整充放电策略。文献[5-8]中依据已有分时电价制定优化策略，并没有将优化策略反馈至电价制定；而文献[10-11]的工作则没有考虑将基础负荷融入负荷电价确立，并且也没有衡量区域内电源结构对于电价波动的影响。同时，分时价格策略依赖于人为观察与制定价格，加之现有研究忽略了地区电源结构、电网拓扑等特性可能会造成的影响，仅利用充放电数据或分时电价引导V2G 策略的制定不够准确。

为克服以往研究中缺少直接采用负荷作为充电电价，以及缺少考虑电源结构以确定电价的情况，本文将以负荷电价作为基础的充放电策略与区域电源调差能力作为基准来制定电价，考虑如何利用电动汽车电池降低区域电网运行峰值负荷与用户充电成本最低，吸引更多电动汽车用户参与V2G 电网优化策略，实现电网侧与用户侧共赢的良性循环。

1 典型充放电与充电电价设定策略

本节将简单介绍充电站结构、典型充放电策略与充电价格设定。在本文算例中，将其他典型策略与充放电价设定作比较。

1.1 充电站结构

可实现电网-电动汽车交互的典型充电站结构如图1 所示。功率由电网主网侧传输，经由变压器至配电网侧，配电网侧再经由交流/直流双向逆变器至直流母线。若仍需要调整电压，则可在直流侧继续接入直流变压器。交流、直流充电桩可接入配电网侧、直流端为电动汽车提供充电服务。为控制电动汽车充电时的功率状态，每个充电桩都安装了充放电控制器[12]。

图1 典型充电站结构

1.2 典型充放电策略

典型充放电策略可分为以下3 种[6]：

（1）充电站仅向电动汽车提供充电服务，不抽取电动汽车电池电量或用户不允许充电站使用其电池为电网提供优化。

（2）充电站可自由使用电动汽车用户电池电量，但必须保证用户在预定时间离开时至少存有规定电量。

（3）与策略（2）相同，充电站可使用电动汽车用户电池提供电网优化服务，但用户考虑中途可能随时取用电动汽车，规定在充放电过程中电池容量存在下限。

1.3 典型充电价格设定策略

电动汽车充电收费策略可分为以下3 种[10]：

（1）充电电价不随时间、负荷等条件改变，任意时刻为常值。

（2）充电电价随时间改变，实施分时电价策略，典型应用为峰谷电价。

（3）充电电价随负荷而调整，建立电价与负荷关系制定负荷电价。

上述3 种常见的电价设定策略中，策略（2）与（3）在本质上是为减少用户在基础负荷高峰期时充电功率，但策略（2）需要事先确定，忽略了基础负荷变化情况，而策略（3）电价直接与负荷建立联系，为优化区域负荷提供了条件。

2 充电电价设定策略

本节将详细阐述如何建立优化策略的充放电模型，并利用充放电策略与本地电源结构的等值调差系数确定充电价格。

2.1 电价函数设计

通过分析充电站的历史区域负荷数据与电动汽车充放电数据，可以将优化时间段分为时刻集合N，所有参与充放电策略的电动汽车集合为M。对于某辆电动汽车用户m∈M 在某个时刻i∈N，其充电状态可用tm，i表示，充电功率大小用xm，i表示。其中tm，i定义如下：

所有充电汽车在所有时刻的充电状态可由T∈{0，1}表示。对于任一电动汽车m，设电动汽车电池容量为，其来到充电站时间为，初始电池电量为，离开充电站时间为，离开时电池电量为。

充电站的收费可按1．3 节设定策略，按常值、峰谷电价以及负荷电价设定。其中负荷电价可由多项式f 表述，其定义为：

式中：L 表示当前负荷；k 表示当前负荷系数。L与k 均为非负数。若计算某时刻i 的用户充电成本，则可由Ci表示：

式中：Lb表示区域内的基础负荷；Lc表示充电站的充放电交互功率之和；Ci表示用户在第i 时刻的充电成本。从式（3）可以看出，Ci是由第i 时刻的基础负荷到总负荷积分值。

由于单个用户的充电选择与行为难以捕捉，但充电站的区域负荷数据与每日充放电车辆行为相对稳定且具有一定规律，可以做出如下适当假设简化模型：

（2）电动汽车m∈M 的电池容量相同，其电池初始容量为正态分布，但必须保证在电动汽车离开时，电池初始容量与最大可充电容量之和大于约定剩余电池容量。

（3）当充电电价随着负荷呈凹函数上升时，其充放电效果相同，则f，C 可简化为：

2.2 约束条件

优化模型中的约束条件主要包括充电功率平衡，电池容量限制，充电功率限制以及充电结束容量限制。

（1）充电功率平衡

对于任意时刻i，充电站与电动汽车的交互功率为Lc。其交互功率Lc必须满足如下等式：

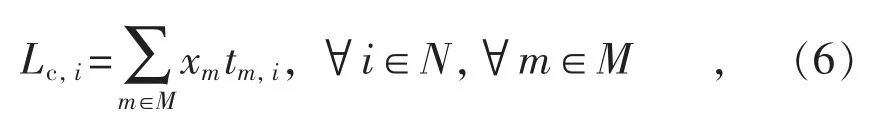
式（6）表示对于任一时刻i，Lc，i与当前时刻处于充放电状态的电动汽车充放电功率之和。

（2）电池容量限制

电动汽车参与到V2G 的任一时刻，其电池容量应符合约束：

任一充电汽车m 在任一时刻i，其电池容量应大于等于0 并且小于等于其最大电池容量。若用户调整其至少保留一定功率，则修改式（7）中左端条件为为电池电量下限系数。

（3）充电功率限制

电动汽车在充电站充放电过程中，其每个优化时间段内交互最大功率负荷为：

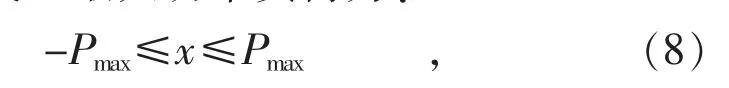
式中：x 表示充放电功率；Pmax表示最大充放电功率。充放电过程中x 应满足充电桩功率限制，若采用仅充电策略，则调整约束条件左端为x≥0。

（4）充电结束容量限制

当电动汽车与充电站达成协议，在停靠充电期间允许充电站使用其电池参与电网优化，则至少在用户离开时应保证电动汽车电池含有τuEcap电量，其中τu为：

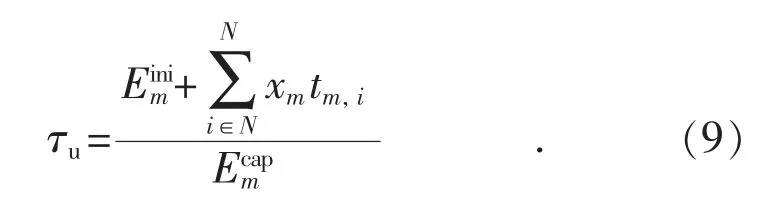
其充电结束容量约束条件为：

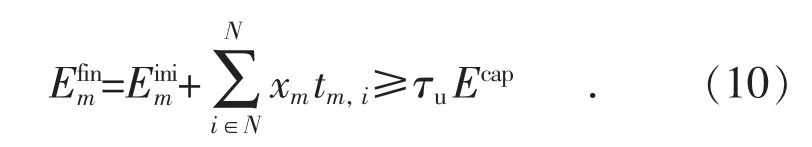
2.3 充放电策略建模

综合上述的假设，目标函数Ctot将考虑最低用户充电成本，可表示为：

式中：k1与k0分别为负荷电价系数；Lb为区域基础负荷；Lc为充放电负荷。为优化用户成本，目标函数为正定二次型规划，属于凸优化模型，可利用内点法或梯度下降等方法有效求得最优解[13]。

为比较其他电价下的充放电策略，充电价格若采用节1．3 中的策略（2），充电电价设置为分时电价，则目标函数为：

式中：kpv为单位分时电价，kpv∈R1×N。

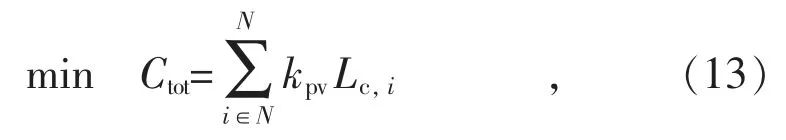
2.4 负荷电价设定

负荷电价制定的本质在于同样的充电量，若在基础负荷较高时则总收费比基础负荷较低时要少。k0代表电价对于基础负荷的成本敏感程度，而k1则表示充电负荷增加的成本敏感程度。

本文描述了在不同电价设置策略下的充放电策略，可最大化降低用户成本，减少电网峰值负荷。由于负荷电价的积分为二次型，充放电策略实质计算的策略中只能得到多项式电价中参数关系。本文的重点研究是价格设定对于电网侧与用户侧充电成本最低，可利用其他最低充电成本建立负荷电价中各参数关系。若用户根据负荷电价调整充电行为则其成本会进一步降低。同时，考虑到充电站带来的负荷波动随机性与本地电源的结构，可利用调差系数参与负荷电价设定[14-15]。

调差系数用以衡量系统的单位调节功率，调差系数越小表示系统对于负荷的功率增加响应更快，可以更快地使用备转容量输出功率，以防止频率下降过快。

等值调差系数σ∑为各个参与调差的发电机单位调节KGi之和的倒数。单台发电机的单位调节功率定义为：

式中：PGi为其发电机输出功率；σ 为发电机额定功率标幺值。系统等值单位调节功率KGN定义为：

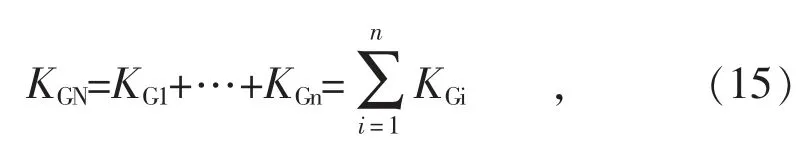
其中，可由调差系数确定参数关系为：

式中：α 为权重。根据上述步骤可设计负荷电价，其流程如图2 所示。

3 算例分析

本文的仿真算例来源于福建省福州市马尾区，区域负荷数据来源于马尾区某区域日负荷数据。所选取电动汽车充电数据来源于2018 年10月3 日马尾区马尾体育馆公共充电站。

分析马尾体育馆充电站中的电动汽车型号、充电功率等参数，抽象出电动汽车的最大电池容量、充电功率等参数得到马尾体育馆充电站仿真参数如表1 所示，进行仿真。

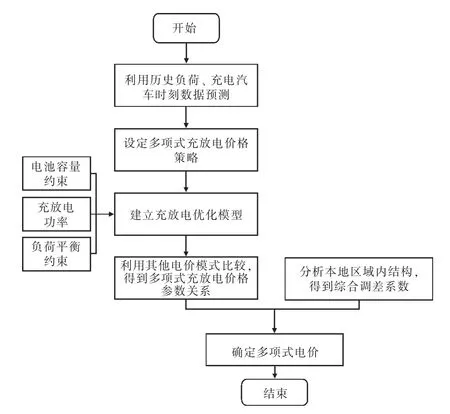
图2 负荷电价设计流程

表1 仿真参数选取

图3 为充电站的电动汽车充电时刻分布图，表示当天某个时刻处于站内的电动汽车数量，马尾体育馆充电站当天共有42 条充电记录。充电需求主要集中在1:00—8:00，此时充电车辆占全天的50%。12:00—17:00 与20:00—24:00 分别为另外2个充电高峰期。全天几乎都有电动汽车在充电，能够覆盖本地基础负荷低峰期与高峰期，从而可通过充放电调节整体负荷均衡。

图3 电动汽车充电时刻分布

图4 则展示了当天充电站内所有充电车辆的充电时长。从图4 看出，绝大多数车辆的充电时长为2～3 h，仅有少部分车充电时长在10 h 以上。因此，此处算法设定参数i 优化时间段间隔为1 h，N 为1 天。

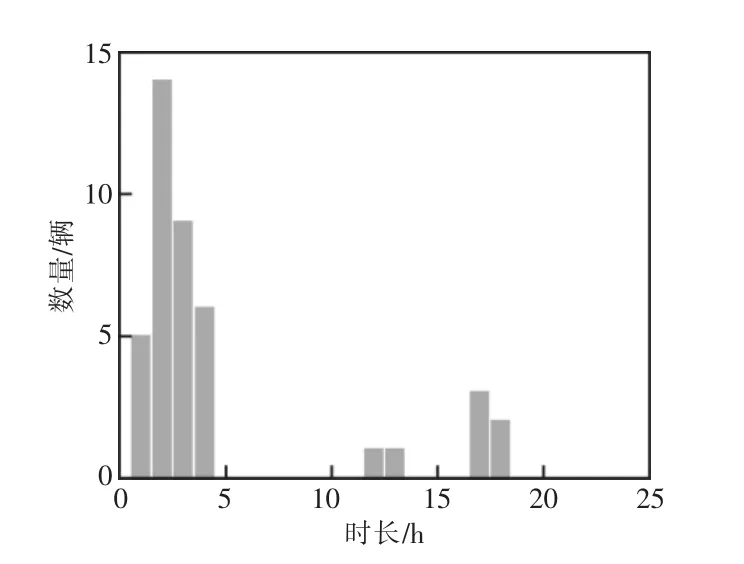
图4 电动汽车充电时长分布

根据区域内基础负荷以及马尾体育馆充电站的不同优化策略，包括优化仅充电策略、自由充放电策略以及电池容量10%剩余的充放电策略对比如图5 所示。

图5 马尾体育馆充放电策略优化比较

图5（a）展示了本地基础负荷，无序充放电与仅允许充电策略结果。相较于无序充放电策略，优化后的充电策略增大了3:00—5:00 与19:00—22:00 的电动汽车充电容量，减少了11:00—15:00时下午高峰时的充电容量，使得本地总负荷峰值由5 508．6 kWh 下降至5 388．6 kWh，下降了大约2．20%。由于仅充电策略不允许抽取电动汽车电池提供电网优化，其无法降低本地基础负荷峰值。图5（b）则展示了使用电汽车电池参与电网削峰填谷优化。从图5（b）看出，充放电优化策略总负荷容量约束充放电策略总负荷相较于仅允许充电优化策略总负荷的峰值大幅度下降。其中充放电策略峰值负荷为4 908．6 kWh，相较于仅允许充电策略的峰值下降了480 kWh，下降8．91%，相较于无序充电策略下降了10．89%。而用户必须保证任意时刻电池电量不低于10%的容量约束相较无约束充放电策略峰值仅上升11．6 kWh，保证用户利益的同时也达到了对区域负荷的削峰填谷效果。

图6 是不同充放电策略下的充放电功率示意图。在允许充放电策略下，控制器将在区域负荷峰值的10:00—15:00 利用电动汽车电池放电供区域负荷使用，降低了电网侧的峰值功率，并且减少了负荷波动。然后在夜间区域负荷较低时开始充电，以保证电动汽车用户的正当利益。

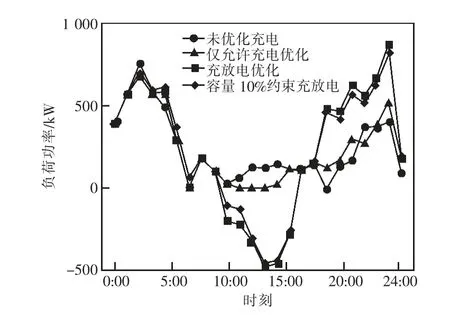
图6 马尾体育馆充电站充放电功率

当利用式（14）峰谷电价进行优化计算时，用户充电成本为4 012．4，相比降低用户成本6．13%。确定负荷电价可利用峰谷电用户成本与区域电源结构利用峰谷电价优化用户成本可得关系式：

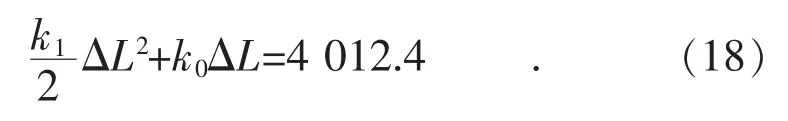
区域内可参与调频的共有16 台100 MW 的水轮机组，20 台75 MW 水轮机组，20 台100 MW汽轮机组，64 台50 MW 汽轮机组与1 600 MW容量汽轮机组，其调频标幺值见表2。若所有机组全部参与调频，根据式（15）与式（16）、式（17）可得到KGN=61．06，据式（18）得到负荷电价关系式k1=0．016 36×k0。若区域内无发电机参与调频，则KGN=0，σ∑=∞，k1=∞，用户成本将趋于无穷。

表2 调频电机标幺值参考

根据上述负荷电价关系，可得到负荷电价系数k1为0．000 254 5，k0为0．015 2，如图7 所示，此时得到用户充电成本与峰谷电价成本相同，且可减少区域峰值负荷480 kWh。

图7 负荷电价确定关系

4 结语

本文针对在充电站实行充放电策略时提出了充电电价制定指导，主要考虑到区域运行的峰值负荷与用户充电成本。首先，分析了区域内历史负荷数据与电动汽车充电数据，可根据区域内的主流电动汽车电池最大容量、充电站充电功率以及电动汽车充电时长规律等设定仿真参数，以适用不同的充电站运营；其次，根据电动汽车电池容量、充放电功率平衡以及用户约束条件下建立充放电策略，降低负荷波动与用户充电成本；最后，综合本地电源结构确立负荷电价。

本文中存在的一些不足和尚未研究的问题将继续寻求改进方案：

（1）若考虑长期优化策略，应将电动汽车用户电池损耗和寿命加入建模优化[15]。

（2）缺少数据对用户对于充电电价的响应建模。