基于自动色阶和多尺度Retinex彩色图像增强算法

冯红波，李 萍，李 波

(宁夏大学 物理与电子电气工程学院，宁夏 银川 750021)

0 引言

图像是人们进行信息交流的重要媒介之一。随着相机以及图像处理技术的发展，人们已经可以获得质量非常高的图像，但是外部环境的复杂(如夜间、雾天等)常常导致我们得到的图像并不是很理想：照射光不均匀、噪声太大等因素出现对比度不足、细节模糊，色彩失真的图像，从而导致很差的视觉体验[1]。当前对图像增强比较经典的算法有基于直方图均衡化的增强算法[2-4]、图像融合的增强算法[5-7]以及基于Retinex的增强算法[8-10]等。其中对于Retinex算法存在很多问题，众多学者提出了许多改进的方法。文献[11]把小波变换与Retinex算法结合运用在遥感图像增强上提高了地表物体细节信息的可读性。文献[12]将边缘提取与Retinex算法结合使增强后的图像细节得到明显提升。

针对光照不均图像使用传统MSR算法增强后出现颜色失真，边缘锐化不足的问题，本文对MSR算法进行改进得到Auto-colorMSR算法。提出一种添加光照因子的MSR算法增强纹理细节，并利用自动色阶与改进后的MSR结合进行颜色恢复。

1 Retinex基本原理

Retinex 是由Edwin Land根据人类视觉系统提出一种图像增强理论，算法名称是视网膜(Retina)和皮层(Cortex)结合而来，根据图像色彩的颜色恒常性，物体的颜色是由物体对于红、黄、蓝3种光波的反射能力决定的，而不受光线因素的影响[13]。依据这一基本理论，一副图像可以分为入射图像L与反射图像R，其中反射图像R体现了图像的本质。Retinex原理图如图1所示。

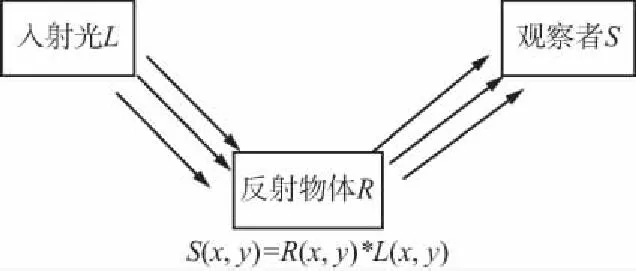
图1 Retinex基本原理

1.1 单尺度Retinex

基于Retinex理论，人类看到的图像可由式(1) 表示。

S(x，y)=L(x，y)*R(x，y)，

(1)

式中，S(x，y)为原始图像；L(x，y)为入射图像，一般是高斯平滑后的图像估计；R(x，y)为反射图像，即图像的内在属性。转换到对数域中得到单尺度retinex算法

lbR(x，y)=lbS(x，y)-lb[F(x，y)⊗S(x，y)]，

(2)

式中，F(x，y)为中心环绕函数，

F(x，y)=λexp[-(x2+y2)/c2]，

(3)

式中，c为高斯环绕尺度，λ为一个尺度，且满足

∬F(x，y)dxdy=1，

(4)

对lbR(x，y)反对数变换到实数域得到增强后的图像。

1.2 多尺度Retinex(MSR)

多尺度Retinex算法(MSR)是对图像多个尺度上的SSR加权求和所得到的，如式(5)所示。

Si(x，y)=Li(x，y)*Ri(x，y)，

(5)

转换到对数域为：

(6)

式中，K为高斯环绕函数的个数，w为权重，当K=1时，MSR算法就等同于SSR算法。一般权重取平均权重，即w1=w2=w3=1/3。高斯处理小尺度能够很好地完成动态范围的压缩，大尺度能够保持色感[5]。一般选择大中小3个尺度，本文算法c参数分别取15，80，250。

2 Auto-colorMSR算法

2.1 算法流程

算法整体流程：首先对待增强图像进行双边滤波去噪处理，然后将图像转换到对数域进行MSR增强，对得到的结果进行自动色阶色彩恢复，最后将结果转换到实数域得到最后的增强图像。算法流程如图2所示。

图2 Auto-colorMSR算法流程图

2.2 去噪处理

双边滤波(Bilateral Filter)是一种非线性滤波函数，它与高斯滤波主要的区别不仅考虑像素的欧式距离还考虑了像素一定范围的辐射差异。它可以在去噪的同时很好地保留边缘信息[14]。双边滤波如公式(7)所示。

(7)

式中，f(x) 和h(x)为输入图像与输出图像的亮度，c和s分别表示空间距离的高斯权重以及像素间相似度的高斯权重。本文选择的c与s都为50。图3为选取的图像及去噪后的图像。

图3 图像去噪

2.3 光照调节因子

由式(1)可知入射图像L(x，y)反映的是图像的动态信息，包括光照、环境等信息。传统MSR算法是建立在图像所受光照均匀的基础上，实际上大多数需增强的图片所受到的光照不均匀。从文献[15]中可以得知如果完全消除光照图像，得到的增强结果会产生不自然的结果。所以在去除光照图像的过程中增加一个光照图像调节因子k(k∈(0，1))，即

lbR(x，y)=S(x，y)-k[lb(F(x，y)⊗S(x，y))]，

(8)

对于MSR算法同样在每个尺度上进行改进得到：

lbRi(x，y)=Si(x，y)-ki[lb(Fi(x，y)⊗S(x，y))]，

(9)

式中，i为3，ki∈(0，1)。从式(9)可以看出在每个尺度上，当k趋近于0时，增强后的图像趋近于原图像；当k趋近于1时，入射图像接近于被完全消除，增强图像会产生对比度不够的不自然现象。因此本文同时考虑两方面，令k1=k2=k3=0.5。

2.3 颜色恢复处理

经过添加光照调节因子改进的MSR算法处理后的图像，再利用自动色阶进行色彩恢复得到增强图像。传统算法为了解决SSR与MSR算法普遍存在的色偏问题，引入了颜色恢复因子C，C的定义如下[11]。

(10)

式中，Ci为第i通道的颜色因子，f为颜色空间的映射函数，

(11)

式中，β为增益函数，α为受控制的非线性强度因子。添加色彩因子的MSRCR算法弥补了MSR色彩失真的缺陷，但是仍存在局部或大面积色彩失真的情况，并且由于增加了许多参数使得算法的效率大大降低。

本文采用自适应色阶与MSR算法相结合来改善增强后图像的色彩失真度。自动色阶的思想是首先利用图像的直方图统计，对于像素值高于高阈值Tmax的像素点设为255，将像素值低于低阈值Tmin的像素点设为0，像素点在Tmin与Tmax之间的保持不变。阈值定义如下。

(12)

(13)

式中，u为log运算后的数值，u0=0，count为统计直方图后u所在的位置，β为可控的色阶因子。本文选用的β=0.05。

图像经过MSR以及自适应色阶后，将结果从对数域转换到实数域得到增强图像。本文采用线性量化的方式得到最终增强的图像，量化公式为

R(x，y)=(lbR(x，y)-min)/(max-min)*255，

(14)

式中，max为每个通道得到的最大值，min为每个通道得到的最小值。利用式(14)分别在R，G，B三通道上进行量化后得到最终增强的图像。增强后的图像如图4所示，可以看出原图像的整体对比度不强，细节模糊严重。经过Auto-colorMSR算法图像对比度提高，没有出现色偏现象，边缘细节保留较好。

图4 增强后的图像

3 实验分析

选取2幅特例图片，用python进行仿真实验。图5(a)类似于一个桥洞，图片整体偏暗，且细节不清晰；图6(a)是高空俯瞰城市的画面，因为存在薄雾，图像整体模糊。图5和图6中的其他小图分别表示MSR，MSRCR，Auto-colorMSR算法增强后的图像。

图5 桥洞增强结果

图6 城市增强结果

3.1 主观评价

人类视觉感官是评价图像一个重要标准。从图5和图6可以看出：经MSR算法增强后图像均出现局部或整体颜色失真，如图5(b)的墙面，图6(b)整体色彩失真；边缘纹理模糊，如图5(b)的对联，视觉效果不好；经过MSRCR算法处理虽然对色彩恢复有了一定的改进，但仍存在图像过增强，如图5(c)和图6(c)颜色整体泛白，以及边缘细节信息模糊等问题。Auto-colorMSR算法增强后图像色彩保真良好且出现过增强，纹理细节保留完好。因此从视觉方面看，Auto-colorMSR算法优于传统的MSR、MSRCR算法。

3.2 客观评价

从客观数据上评价算法效果，选用图像均值、标准差以及熵3个方面对算法效果进行评估。图像的均值体现了图像整体的明暗情况，均值越接近中值，图像越理想，对于人类的视觉体验越好；图像标准差体现了图像的对比度，标准差越大，图像对比度越高；熵即图像的信息熵，描述的是图像想的平均信息量，熵也大，图像纹理越清晰，色彩越丰富。熵的定义如式(15)所示[16]。

(15)

式中，pi表示每个灰度级i出现的概率。

2张图像的客观评价结果如表1和表2所示。表1为测试桥洞图像所得到的数据，可以看出本文算法优于其他2种算法；表2除个别数据没有优于其他2种算法，其他也都优于比较算法。由客观数据可以看出本文算法既能保证人类视觉体验(接近均值127.5)又能够保证增强后的图像的色彩以及细节纹理的清晰。

表1 桥洞定量评价指标对比

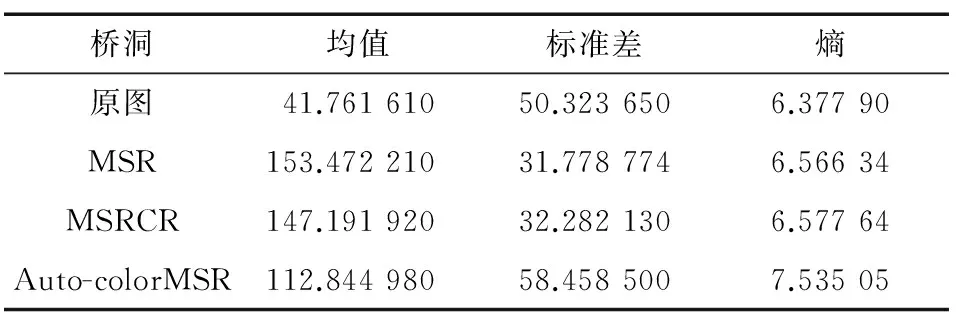
桥洞均值标准差熵原图41.761 61050.323 6506.377 90MSR153.472 21031.778 7746.566 34MSRCR147.191 92032.282 1306.577 64Auto-colorMSR112.844 98058.458 5007.535 05

表2 城市定量评价指标对比

城市均值标准差熵原图109.873 1436.215 257.003 82MSR133.909 2130.907 696.811 81MSRCR130.373 1030.933 196.801 91Auto-colorMSR149.864 4660.112 277.664 24

4 结束语

针对传统MSR算法在处理光照不均图像时存在的问题，本文提出了基于自动色阶和MSR的Auto-colorMSR算法。结论主要包括：① 使用MSR算法的理想条件为图像所受的光照均匀，对于光照不均图像不应完全去除光照图像；② 自动色阶与MSR算法结合进行颜色恢复，相较于加入色彩因子的MSRCR不仅参数减少，而且色彩恢复更好，没有出现失真现象；③ 实验数据表明，相较于MSR、MSRCR法，本文算法更加有效提升图像的对比度，使增强图像具有更好的色彩保度。体现了本文算法的优越性。

本文算法的参数需要人工设定，下一步将对算法进行改进为自适应图像的Auto-colorMSR算法，并应用于批量图像增强处理。