含Smarandache LCM函数的一类复合数论函数方程的可解性
张明丽,高 丽
(延安大学 数学与计算机科学学院,陕西 延安 716000)
上世纪末,Smarandache[1]定义并研究了若干新的数论函数问题。近年来,关于Smarandache以及系列Smarandache衍生函数与其他数论函数方程相互结合求解及相关性质的研究备受关注。张天平[2]对复合函数方程φ(φ(n))=2Ω(n)的奇数解进行了研究;田呈亮[3]对复合函数方程φ(φ(n))=2Ω(n)的正整数解进行了研究;多布杰[4]对复合函数方程φ(φ(n))=2t的可解性问题进行了研究。近期,王洋、张四保、袁合才、王波等[5-6]先后对复合函数方程φ(φ(n-φ(φ(n))))=2,4,6的可解性问题进行了讨论。张利霞、赵西卿、郭梦媛、高丽等在文献[7-9]中分别研究了数论方程S(SL(n))=φ(n),
S(SL(n))=φ2(n),S(SL(n2))=φ2(n)的可解性。本文进而对含Smarandache LCM函数的复合数论函数方程φ(φ(n-S(SL(n))))=2,4的可解性问题进行了探究。
1 相关定义及引理
定义1[7]对于任意的正整数n,Euler函数φ(n)定义为在序列1,2,…,n-1中与n互素的整数的个数。
定义2[7]Smarandache函数S(n)表示为,对于任意的正整数n,有
S(n)=min(m∈Z:n|m!}。
定义3[7]Smarandache LCM函数SL(n)表示为,对于任意的正整数n,若n=p1r1p2r2…pkrk,其中所列的p1,p2,…,pk均为素数且顺序排列,则有
SL(n)=max{p1r1,p2r2,…,pkrk}。
引理1[8]若正整数n=p1r1p2r2…pkrk,其中p1,p2,…,pk为素数,则欧拉函数
Smarandache函数S(n)=min{m∈Z:n|m!},
Smarandache LCM函数SL(n)=max{p1r1p2r2,…,pkrk}。
引理2[9]:当n≥2时,有φ(n) 引理3[9]:对于整数k和素数p,有S(pk)≤kp;当且仅当k 证明:由引理1—引理3易知,当满足条件时, 定理1 含Smarandache LCM函数的复合数论函数方程 φ(φ(n-S(SL(n))))=2 (1) 的正整数解为n=10,15,16,18,14,12,21,27。 证明:因为φ(φ(n-S(SL(n))))=2,所以 φ(n-S(SL(n)))=3,4,6。下面分3种情况加以讨论: 情形一:若φ(n-S(SL(n)))=3,由引理2可知式(1)无解。 情形二:若φ(n-S(SL(n)))=4,则 n-S(SL(n))=5,8,10,12。 当n-S(SL(n))=5时,由引理4,此时6≤n≤10,将其逐一代入验证,只有n=10满足 n-S(SL(n))=5,即n=10为式(1)的解。 当n-S(SL(n))=8时,由引理4,此时9≤n≤16,将其逐一代入验证,此时式(1)无解。 当n-S(SL(n))=10时,由引理4,此时11≤n≤20,将其逐一代入验证,只有n=15,16满足 n-S(SL(n))=10,即n=15,16为式(1)的解。 当n-S(SL(n))=12时,由引理4,此时13≤n≤24,将其逐一代入验证,只有n=18满足 n-S(SL(n))=12,即n=18为式(1)的解。 情形三:若φ(n-S(SL(n)))=6,则 n-S(SL(n))=7,9,14,18。 当n-S(SL(n))=7时,由引理4,此时8≤n≤14,将其逐一代入验证,只有n=14满足 n-S(SL(n))=7,即n=14为式(1)的解。 当n-S(SL(n))=9时,由引理4,此时10≤n≤18,将其逐一代入验证,只有n=12满足 n-S(SL(n))=9,即n=12为式(1)的解。 当n-S(SL(n))=14时,由引理4,此时15≤n≤28,将其逐一代入验证,只有n=21满足 n-S(SL(n))=14,即n=21为式(1)的解。 当n-S(SL(n))=18时,由引理4,此时19≤n≤36,将其逐一代入验证,只有n=27满足 n-S(SL(n))=18,即n=27为式(1)的解。 定理2 含Smarandache LCM函数的复合数论函数方程 φ(φ(n-S(SL(n))))=4 (2) 的正整数解为n=20,25,24,32,36,22,33,26,28,39,35,40,48。 证明:因为φ(φ(n-S(SL(n))))=4,所以 φ(n-S(SL(n)))=5,8,10,12。下面分4种情况加以讨论: 情形一:若φ(n-S(SL(n)))=5,由引理2可知式(2)无解。 情形二:若φ(n-S(SL(n)))=8,则 n-S(SL(n))=15,16,20,24,30。 当n-S(SL(n))=15时,由引理4,此时16≤n≤30,将其逐一代入验证,只有n=20,25满足 n-S(SL(n))=15,即n=20,25为式(2)的解。 当n-S(SL(n))=16时,由引理4,此时17≤n≤32,将其逐一代入验证,此时式(2)无解。 当n-S(SL(n))=20时,由引理4,此时21≤n≤40,将其逐一代入验证,只有n=24满足 n-S(SL(n))=20,即n=24为式(2)的解。 当n-S(SL(n))=24时,由引理4,此时25≤n≤48,将其逐一代入验证,只有n=32满足 n-S(SL(n))=24,即n=32为式(2)的解。 当n-S(SL(n))=30时,由引理4,此时31≤n≤60,将其逐一代入验证,只有n=36满足 n-S(SL(n))=30,即n=36为式(2)的解。 情形三:若φ(n-S(SL(n)))=10,则 n-S(SL(n))=11,22。 当n-S(SL(n))=11时,由引理4,此时12≤n≤22,将其逐一代入验证,只有n=22满足 n-S(SL(n))=11,即n=22为式(2)的解。 当n-S(SL(n))=22时,由引理4,此时23≤n≤44,将其逐一代入验证,只有n=33满足 n-S(SL(n))=22,即n=33为式(2)的解。 情形四:若φ(n-S(SL(n)))=12,则 n-S(SL(n))=13,21,26,28,36,42。 当n-S(SL(n))=13时,由引理4,此时14≤n≤26,将其逐一代入验证,只有n=26满足 n-S(SL(n))=13,即n=26为式(2)的解。 当n-S(SL(n))=21时,由引理4,此时22≤n≤42,将其逐一代入验证,只有n=28满足 n-S(SL(n))=21,即n=28为式(2)的解。 当n-S(SL(n))=26时,由引理4,此时27≤n≤52,将其逐一代入验证,只有n=39满足 n-S(SL(n))=26,即n=39为式(2)的解。 当n-S(SL(n))=28时,由引理4,此时29≤n≤56,将其逐一代入验证,只有n=35满足 n-S(SL(n))=28,即n=35为式(2)的解。 当n-S(SL(n))=36时,由引理4,此时37≤n≤72,将其逐一代入验证,只有n=40满足 n-S(SL(n))=36,即n=40为式(2)的解。 当n-S(SL(n))=42时,由引理4,此时43≤n≤84,将其逐一代入验证,只有n=48满足 n-S(SL(n))=42,即n=48为式(2)的解。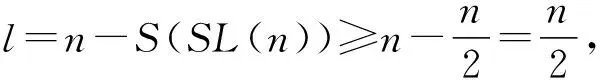


2 主要结论及其证明

