生成有限拓扑的负载均衡算法*

陈建兵， 梁立， 叶志霞

(1.云南师范大学 信息管理处,云南 昆明 650500；2.云南师范大学 信息学院,云南 昆明 650500)

1 引 言

有限拓扑是指有限集合的拓扑：由n元集合X的子集生成的集族T满足：

(1)可行性：Φ,X∈T

(2)封闭性：对任意的A,B∈T都有A∪B∈T且A∩B∈T

则称集族T是X的一个拓扑.

1元集合X的拓扑只有1个：{Φ,X}；2元集合有4个拓扑，3元集合有29个拓扑，4元集合有355个拓扑，5元集合有6 942个拓扑，6元集合有209 527个拓扑，……，10元集合有8 977 053 873 043个拓扑[1]……

在早期，用枚举法生成拓扑并计数[2]，计算量相当庞大.n元集合的所有集族有22n个，即使只枚举满足可行性的集族，也需要检验22n-2个集族的封闭性，计算量仍然庞大.而且拓扑占有集族的比例相当低[3]，说明枚举法做了大量的无效计算.赵婷婷根据文献[4]的构造定理，得到了文献[5]和[6]的递推算法，大大减少了无效的计算，但算法的时间复杂度仍然是非多项式的.拓扑数量的下界[7]是2n2/4也表明了这是一个NP难问题，即使完全有效的计算，计算量也很惊人的.因此，构造并行算法很有必要，而负载均衡技术是有效发挥并行计算的关键.

2 递推算法

2.1 有关概念

设n元集合Xn的拓扑T={Φ,A1,…,Ak,Xn}，则

(1)拓扑长度：拓扑中非空真子集的个数，即|T-{Φ,Xn}|，取值范围0～2n-2.平庸拓扑的长度最小为0，离散拓扑的长度最大为2n-2.

(2)拓扑元数：拓扑中所有非空真子集的并所含元素个数，即|∪A∈T-{Φ,Xn}A|，取值范围0～n.只有平庸拓扑的拓扑元数为0.称Smax=∪A∈T-{Φ,Xn}A为T的最大子集.

如果拓扑元数小于n，则称T为α拓扑；如果拓扑元数等于n，则称T为β拓扑.

(3)直和运算：设Xn的集族J={J1,J2,…,Jm},x∈Xn，则J⨁{x} ={J1∪{x},J2∪{x},…,Jm∪{x}}称为J与x的直和运算，简记为J⨁x.

2.2 递推算法

n元集合Xn={x1,x2,…,xn} 的所有拓扑由n-1元集合Xn-1的每一个拓扑生成[5-6].对每一个n-1元集合的拓扑T={Φ,A1,…,Ak,Xn-1}，由下面T1-T5五步产生n元集合的拓扑(新拓扑)：

T1:T1=T∪{Xn}

T2:T2=T∪(T⨁xn)

T3: 对每一个Ai∈T-{Φ,Xn-1}，T3=T∪(J⨁xn),其中J={Aj|Ai⊆Aj,Aj∈T}

T4: 对每一个Ai∈T-{Xn-1}，T4=(T⨁xn)∪J,其中J={Aj|Ai⊇Aj,Aj∈T}

T5：如果∪A∈T-{Φ,Xn-1}A≠Xn-1，则产生T5=(T-{Xn-1})∪{Xn}，并计算T6

计算T6：

Call max_main(Smax∪{xn}，Φ，T5，T5-Xn)

对每一个Ai∈T5-{Φ,Xn}

T6=T5∪J,其中J={Aj|Ai⊆Aj,Aj∈T5-{Φ,Xn}}⊕xn

Call max_main(Smax∪{xn}，Ai∪{xn}，T6，J)

下面的过程max_main是计算T6的一个子例程：

procedure max_main(Smax,Smain，Told，J)

{

C=Xn-Smax

对每一个C1∈2C，C1≠Φ

D=J⨁C1⨁xn={D1,……,Dh}，其中Di=Ji∪C1∪{xn}，Di≠Xn

对每一个Di∈D

ifDi>Smain

G=Told∪H,其中H={Dj|Di⊆Dj,Dj∈D}

如果G是拓扑

把G赋给T6

Call max_main(Smax∪Di，Di，T6，J∪H)

}

对每一个n-1元集合的拓扑T，在T1-T2每一步只产生一个新拓扑；T3-T4会产生多个新拓扑；T6是在产生T5之后才计算(只有T是α拓扑才产生一个T5，也才会计算T6).

对每一个n-1元集合的拓扑T产生新拓扑的任务都是独立的，所以算法并行化是很容易的.分布式内存并行计算的加速比很高(MPI易于实现)，对每一个空闲的CPU都可以立即分配一个新的T，然后独立完成T1-T6步；而共享内存的并行计算存在多个计算任务等待的情况(主要是第T6步的计算量差异较大)，按照α拓扑进行分类等待的时间会大大减少 (OpenMP易于实现共享内存的并行算法) .

这个算法的时间复杂度比早期的一些算法有了很大的改进，计算量几乎就是拓扑数量，只有T6的计算有冗余.

3 负载均衡算法

上述的递推算法T1-T5每一步之间是相互独立的，没有耦合，它们只依赖n-1元集合的拓扑T，容易实现算法的并行计算.但是，每一个T所需要计算的时间不同，T1-T5每一步所花的时间差异很大，所以并行计算的负载均衡很重要.下面7种并行计算方法主要考虑负载均衡的问题：

(1)对每一个T，用5个CPU分别计算T1-T5.显然，T1-T2容易计算；T3-T4计算时间与T的长度有关；如果T是α拓扑那么计算T5之后还需要计算T6，计算时间与T的长度和拓扑元数都有关系，如果T不是α拓扑就不需要计算T5.显然，5个步骤的计算量很不均衡.

(2)假设有CPUs个CPU，把T1-T5合并起来视为一个函数f(T).读取CPUs个T之后再让每个T分配一个CPU调用f(T)实现并行计算.根据(1)的分析，每一个T的长度和拓扑元数的不同，调用f(T)所需要的计算时间差异也很大.每个T的结构不同而导致每个CPU的计算量很不均衡.

(3)把所有的T归类.拓扑元数相同且拓扑长度也相同的T归为一类.把同一类CPUs个T同时调度CPUs个CPU，最后剩余的T做一次善后处理.因为n-1元集合的拓扑数量很大，把它们同时放在内存是不现实的，而且各类拓扑分布零散不容易归类，所以这是一种理想方法，难以实现.下面的三种方法是基于这种理想方法而逐步改进的.

(4) 把α拓扑和β拓扑交叉计算.设两个函数α(T)和β(T)，α(T)包含了T1-T5的计算，β(T) 包含了T1-T4的计算.如果T的拓扑元数小于n-1则调用给α(T)， 否则调用β(T).α拓扑和β拓扑可能交叉出现，这是一种容易实现的并行算法.不同的T调用β(T) 的计算量比较相近，但是α(T) 的计算任务差异很大，因此负载也很不均衡.

(5)改进第(4)种方法，把α拓扑和β拓扑分开计算.对n-1元的所有拓扑扫描两次：第一次处理n-1元的α拓扑，第二次处理n-1元的β拓扑.实验表明，这种方法比前面几种方法在负载均衡的性能上有了明显的改善，但是拓扑元数差别很大的两个α拓扑，它们的计算时间相差也很大.

(6)改进第(5)种方法，按拓扑元数归类，仍然采用两次扫描.用一个二维数组Tα[n-1][CPUs] 缓存α拓扑，当某一个拓扑元数i存够了CPUs个T，立即把Tα[i](i=0,1,…,n-2)分配给CPUs个CPU，调用α(T)并行计算.类似，用一个一维数组Tβ[CPUs] 缓存β拓扑，当存够了CPUs个T就分配CPUs个CPU调用β(T)并行计算.

方法(6)无论是数组Tα还是Tβ都没有考虑拓扑长度归类的问题.事实上，由于拓扑长度的取值范围比较大，而且按长度分布的拓扑比较稀疏，按长度归类是很难实现的.影响计算量的主要因素是拓扑元数，也就是α(T)中T5步的计算是影响计算量的主要因素.

(7)分配CPUs个CPU，每个进程完成了T1-T5的全部计算之后，不等待其他进程而直接读取新的T，直到全部T处理结束.

方法(7)可以使分配的CPU长期处于高利用状态，但存在两个负担：一是每个CPU全程负责一个T的递推，在读取新数据的时候需要“互斥”处理；二是由于每个T所需时间差异很大，在任务结束前，可能导致长时间等待某个进程结束才完成整个任务.实验发现，把β拓扑放到最后处理确实有明显的效果，原因是在任务结束前不需要计算T6.因此方法(7)具有非常好的负载均衡性能.

4 算法实验

在上面讨论的七种并行算法中，计算结果都一样，不一样的是算法的计算时间.不同的计算时间是由负载均衡的性能决定的.方法(1)和(2)的负载极不均衡，方法(3)难以实现，方法(5)是方法(4)的改进.因此，在本节中只给出方法(5)-(7)的实验数据，可以看到这三种方法逐步趋于较好的负载均衡状态.

用OMP共享内存并行程序设计[8]，使用64个CPU对方法(5)-(7)进行实验.在相同的云计算环境下，方法(5)-(7)的计算时间对照如表1.从实验数据可以看出方法(7)的计算时间有大幅度的减少，说明从方法(5)到方法(7)的改进是有效的.

表1 几种并行计算时间对照表

从图1-图3可以看出，方法(7)的计算过程比较稳定，CPU的使用率较高.总体而言无论从计算时间还是计算过程的稳定性的角度分析，方法(7)的负载均衡性能基本趋于最佳状态.

图1 方法(5)的运行记录截图

图2 方法(6)的运行记录截图

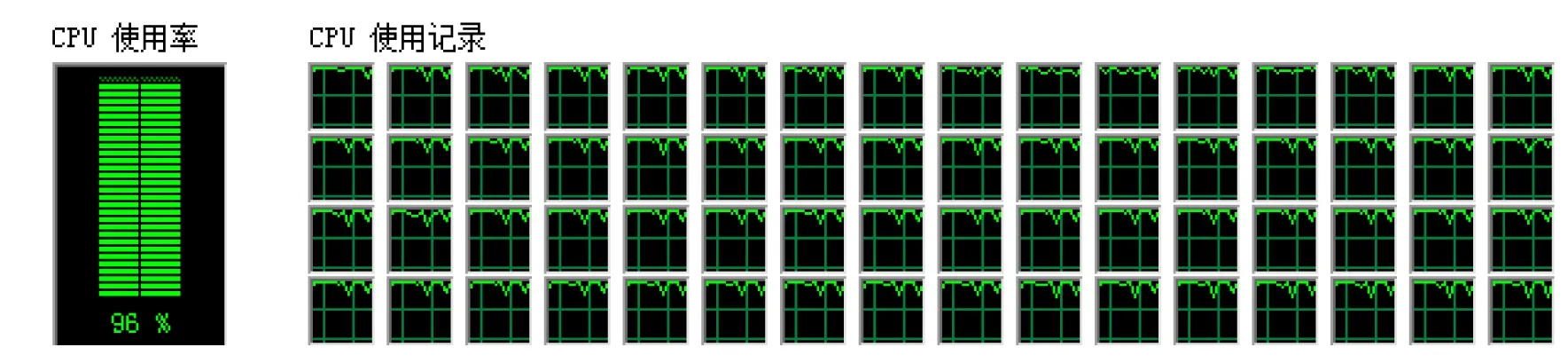
图3 方法(7)的运行记录截图

5 结 论

上述算法和实验中，除了拓扑长度和拓扑元数对负载均衡有较大影响外，每一类数据使用CPU的个数对负载均衡影响也不小.

方法(5)-(7)是基于数据归类的思想而实现负载均衡的.实验表明是可行而且非常有效的.如果再动态调整CPU数，会使算法的负载均衡性能达到更佳的状态.方法(7)不需要考虑算法的耦合度，是比较普适性的方法.

另外，如果用文件存储n-1元集合的拓扑数据，数据量很大，存为CPU个文件比较好：一是读写数据相对快，二是每一个线程单独读或写一个文件，不需要解决互斥的问题.对同一个CPU，先处理α拓扑之后紧接着处理β拓扑，因为处理α拓扑比β拓扑更花时间，如果顺序颠倒，很有可能线程之间需要等待才能全部结束，尤其是共享内存的并行计算的算法这一点更重要.