一款基于码型检测SS-LMS算法的自适应均衡接收器

冯琪琛，俞 剑，徐烈伟，陈更生

(1.复旦大学 专用集成电路与系统国家重点实验室，上海 201203；2.上海复旦微电子集团股份有限公司，上海 200433)

随着半导体工艺的持续进步，芯片的工作频率、规模和数据处理能力不断提高，对芯片的数据交互和吞吐能力的要求也越来越高，持续增长的高速数据传输需求导致I/O的带宽大约每24个月翻倍1次[1].因此，大规模数字信号处理芯片，例如最新的FPGA芯片，配备有多达64条高速I/O通道且每条通道的数据传输速率均超过了10Gb/s，总数据传输带宽超过了1Tb/s[2].高速的数据传输给信号的接收带来了由信道损耗所引起的信号完整性问题，同时信号在背板通道传输中的反射与噪声也会影响到高速信号的可靠传输和接收.图1(a)所示为实测得到的88cm长度背板通道的频率响应曲线，在12.5Gb/s传输速率下，其半波特率的衰减达到了-23.25dB.图1(b)所示为此信道在12.5Gb/s传输速率下的单位脉冲响应，可以看到，信道的衰减使得高速脉冲的波形在接收端被展宽到大于1个单位间隔(Unit Interval, UI)，对前位数据和后位数据都产生了严重的码间干扰(Inter Symbol Interference, ISI)，分别被称为ISI的前标(pre-cursor)分量和后标(post-cursor)分量.

图1 背板通道损耗以及对应通道的单位脉冲响应Fig.1 Backplane channel loss and unit pulse response of the corresponding channel

为克服ISI带来的问题，高速接口电路设计中通常采用线性均衡器例如前馈均衡器(Feed Forward Equalizer, FFE)、连续时间线性均衡器(Continuous Time Linear Equalizer, CTLE)和非线性均衡器例如判决反馈均衡器(Decision Feedback Equalizer, DFE)，或是这些均衡器的组合[3-4]来补偿通道损耗，以使高速接口在10Gb/s以上的数据传输速率下仍然能获得稳定的信号接收.此外，在一些高速接口中，固定系数的均衡器设计往往使得这些接口不能适应不同的背板通道[5]，也无法很好地适应信道特性跟随外界环境如温度、湿度等的变化而随时发生的变化.为了能够实时跟踪并处理信道的变化，需要在均衡器中加入自适应算法进行控制，例如LMS算法、Zero Forcing算法[6]等.其中，LMS算法根据标准数据与均衡后的数据之间的误差来调整均衡器系数，使均衡器系数可以无偏地收敛到维纳解并利用有限精度实现算法的稳定性，使LMS算法成为稳定性最好、应用最为广泛的自适应算法，但LMS算法仍存在两个严重不足: 1) 需要引入额外的标准数据进行比较，在高速通信接口的芯片设计中其实现的成本很高；2) 在计算迭代因子时需要进行数据乘积，乘法器的引入也加大了芯片中数字设计的开销.为降低芯片开销，文献[7]采用模拟电路来实现LMS算法，其移植性差且收敛不稳定.SS-LMS算法使用符号代替数值并采用固定变化步长，具有低计算复杂度和平稳收敛的优点.利用SS-LMS算法，文献[8-9]对多抽头DFE参数进行自适应调节，使得接收速率可以达到20Gb/s以上.文献[10]采用SS-LMS控制下的IIR-DFE设计，在保证均衡效果的同时降低了接收器功耗.文献[11]则针对SS-LMS算法需要额外标准训练数据的缺点进行了改进，采用检测数据位以及数据位之间的上升/下降沿信息，来摆脱对额外的标准训练数据的依赖，但文献[11]算法的一个明显缺点是其自适应均衡的收敛时间较长，影响了接收器的灵敏度.针对上述问题，本文对SS-LMS进行了改进，提出了一种基于码型检测SS-LMS算法的自适应均衡设计，采用数字状态机检测接收数据的码型，通过参考基准电压与接收信号的比较，并对DFE与CTLE结构的改进设计，实现了SS-LMS算法对均衡器系数的自适应控制，同时提高了自适应均衡的收敛速度.

1 基于SS-LMS算法控制的均衡器原理

1.1 DFE均衡原理

图2所示为传统DFE结构示意图，u(n)为n时刻的输入信号，u(n)均衡后的信号q(n)经采样符号化后得到y(n)，其前M位组成向量Y(n)=[y(n-1)，y(n-2),…，y(n-M)]H，向量W(n)=[ω1(n)，ω2(n),…，ωM(n)]H是n时刻的抽头权值(系数).DFE的工作原理是： 将符号化后的输入信号Y(n)与DFE的抽头系数W(n)相乘，得到的乘积项再与输入信号u(n)相减以均衡经过信道衰减后的输入信号.通过对抽头系数W的优化，可以达到消除不同传输条件下ISI后标分量的目的.

图2 传统的DFE框图Fig.2 The block diagram of conventional DFE

1.2 半速率预处理的DFE结构

传统DFE结构存在着关键路径上的频率限制: 为了完全消除ISI后标分量，反馈信号必须在下一个码元进入比较器进行判决之前被准确地反馈到数据输入端以进行加权求和，这就要求DFE中由第1抽头组成的关键反馈路径(即抽头系数的乘积、输入信号均衡求和、比较器对均衡后信号的符号化、以及反馈路径等所引入的所有延迟之和)小于1个数据周期(1个UI).为提高DFE以及整个接收器的工作频率，文献[12]提出的半速率预处理结构，可以有效地缓解DFE在反馈路径上的时序要求.如图3所示，首先将接收器分为奇偶2个并行通道，使用半速率时钟的上升沿和下降沿对输入同时进行采样，生成奇偶2路采样信号.同时将第1个抽头展开，通过使用2个接收数据比较器分别得到接收信号+H1与-H12种结果后，使用另外一条通路上已锁存得到的数据值选择不同的叠加结果以达到准确的均衡结果.通过这种预处理方式，传统DFE中由H1抽头构成的关键路径被转变成了比较器的采样延迟+选择器延迟，缓解了时序限制.H2～HM抽头虽然没有进行预处理，但由于半速率时钟的使用，其对反馈路径延迟的要求放宽到2个UI.因此通过速率预处理结构可以进一步提高DFE以及接收器的工作频率，本文将在2.2节中详细介绍所采用的DFE具体结构.

图3 半速率预处理结构DFEFig.3 Half-rate speculative architecture of DFE

1.3 基于SS-LMS的自适应均衡

DFE的均衡效果取决于滤波器系数的选择.为消除不同信道衰减造成的ISI，常用的方法是采用自适应算法控制DFE的抽头系数，匹配信道以达到最佳的效果.LMS(Least Mean Square)自适应算法是根据计算均衡器输出的误差数据(期望数据与实际输出结果的差值)，优化调整均衡器的抽头系数使均衡器实际输出与期望输出的均方误差(Mean Squared Error, MSE)达到最小值，从而准确地匹配和均衡传输信道[13].在LMS算法中，均衡器输出与所对应的误差数据相乘，再乘以一个步长值μ后得到自适应调整抽头系数的修正因子，最后将其与均衡器原先抽头系数相加得到新的抽头系数.因此，LMS算法存在的缺点是M个抽头的均衡器在每次计算修正因子时需要进行2M次数据乘积，不利于用数字电路实现.

SS-LMS(Sign-Sign Least Mean Square，符号最小均方误差)算法对此加以了改进，在计算修正因子时将均衡器输出结果与误差数据均符号化成+1和-1，以利于数字电路的实现，其计算公式可以表示为

W(n+1)=W(n)-μ·Y[n]·e(n)，

(1)

其中: 向量Y(n)=[y(n-1)，y(n-2),…，y(n-M)]H为符号化后的经过均衡的输入信号；e(n)=sign[d(n)-q(n)]为符号化后的n时刻误差数据；μ为迭代计算的步长；向量W(n)=[ω1(n)，ω2(n),…，ωM(n)]H是n时刻的DFE抽头系数值，W(n+1)=[ω1(n+1)，ω2(n+1)，…，ωM(n+1)]H是n+1时刻的值.

在n时刻，DFE抽头系数迭代计算分为两步，如图4所示: 首先将DFE均衡结果q(n)与对应的期望数据d(n)的差值符号化(sign)后得到误差数据e(n)，与符号化(sign)后、经过均衡的输入信号向量Y(n)相乘，再经过迭代步长μ的调整，得到n时刻抽头系数向量的修正因子μ·Y(n)·e(n)；然后，将修正因子与当前时刻的抽头系数W(n)求差，得到迭代计算后的抽头系数值W(n+1).

图4 使用SS-LMS控制的自适应DFE结构Fig.4 Structure of self-adaptive DFE controlled by SS-LMS

由于Y(n)与e(n)是符号值，因此Y(n)·e(n)可使用查找表实现，同时步长μ的乘积可使用移位实现，从而减小了数字电路的实现代价.

然而如图4（@@@444页）所示，SS-LMS算法中在接收器中引入了外部输入的标准数据d(n)，意味着在接收数据时，需要间隔提供额外的标准数据训练序列对DFE的抽头系数进行训练，使得接收器不能实时、动态地适应信道的环境变化，其训练的过程也会降低数据的有效传输率.针对上述传统SS-LMS算法需要额外的标准数据训练序列的不足，本文对SS-LMS算法的自适应均衡过程进行了改进.如图5（@@@444页）所示，y(n)是符号化后的采样数据，因为LMS算法控制的均衡器收敛后，其均衡输出信号幅值为输入信号的平均幅值，因此本文改进算法采用平均差分幅值VP和符号化后的y(n)的乘积作为近似标准数据，代替标准数据d(n).此时均衡器误差数据e(n)=sign[VP·y(n)-q(n)]，自适应均衡的迭代计算方式保持不变.随着均衡器实际输出q(n)与本地产生的期望数据VP·y(n)之间的MSE逐渐迭代减小，VP·y(n)与d(n)之间的MSE亦趋于最小，从而使最终的均衡器实际输出q(n)与d(n)的MSE最小.改进后的SS-LMS算法，在保证初始误码率维持在一个较低水平的基础上，不再需要额外的标准输入训练序列，在有效匹配和均衡信道的同时，提高了信号的有效传输速率.

图5 使用改进的SS-LMS实现的DFE结构Fig.5 Structure of self-adaptive DFE controlled by improved SS-LMS

改进算法采用MATLAB/Simulink进行仿真和验证，产生随机序列并进行理想输出，经过带有信道损耗、串扰与噪声的信道，最终使用SS-LMS调整的DFE进行信号恢复与判决.分别使用带有期望数据输入的传统SS-LMS算法与本文改进的SS-LMS算法对DFE进行控制，待DFE抽头系数收敛后，得到张开的信号眼图，2种算法的性能对比结果如图6所示.

图6 2种算法性能对比Fig.6 Performance comparation of two algorithms

图6(a)中显示了有训练序列的传统SS-LMS算法与本文改进的SS-LMS算法的DFE抽头随时间的收敛曲线.可以看到，在开始阶段，由于DFE恢复后判决得到的数据误码率依然较高，同时本地产生的输入幅值电压也还没有建立，因此在没有训练序列的情况下，在开始阶段收敛速度较慢.随着抽头系数的值逐渐增大，恢复得到的数据误码率下降，同时VP值迅速收敛到输入差分电压的均值，此时通过接收端本地产生的期望数据逐渐与训练序列中的期望数据变得一致，2种情况得到的收敛曲线最终重合.总体而言，本文的改进SS-LMS算法，在不依靠收敛序列的情况下，抽头系数的收敛速度并没有太大的差距.图6(b)所示为误码率随时间的变化关系，同样在开始阶段由于使用无训练序列的SS-LMS算法控制DFE抽头系数变化收敛稍缓，得到的误码率也较高，但随着抽头系数的收敛，两种算法得到的误码率均趋近于0.因此，本文改进设计的SS-LMS算法，采用内部产生基准电压值和均衡后数据的乘积，近似替代期望数据的输入，消除了传统SS-LMS算法对于期望数据输入的依赖，同时很好地保持了传统SS-LMS算法的总体性能和稳定性.

1.4 基于SS-LMS的CTLE

如1.1节所述，M抽头DFE可以很好地消除M个UI之前的ISI后标分量，但是输入信号的ISI的前标分量与长拖尾后标分量尚没有被很好地消除.与DFE的时域均衡不同，CTLE是一个频域的高通滤波器用以补偿信道的高频衰减，使信道+接收器的整个传输系统的频率特性达到无失真的传输特性.CTLE可以同时有效地消除ISI前标与后标分量，且相较于DFE其电路实现也较为简单.然而，由于CTLE在放大高频分量的同时也放大了高频噪声和串扰，反而会增大信号的误码率，因此需要与DFE组合使用.如图1(b)所示，当12.5Gb/s的高频脉冲经过半波特率的衰减为-23.25dB的信道后，1～7 UI的ISI后标分量较大，这部分分量在高速信号传输中产生的影响占据主要地位，长拖尾后标分量与前标分量较小.因此，本文在折衷考虑均衡器整体性能与功耗的基础上，采用了7抽头(7-tap)DFE和CTLE的组合设计，既能准确地消除1～7UI内的ISI后标分量，同时也可以有效消除ISI前标分量与长拖尾的后标分量.

本文采用了与文献[6]相类似的CTLE结构，采用带有退化电阻电容的两级差分缓冲器以产生低频零点fz与极点fp1来得到高通的幅频特性.针对此种结构，如图7所示，可以通过改变并联电阻的数量，来改变退化电阻的大小和零点的频率.从而改变高低频增益比值，补偿不同通道的不同程度衰减.同样，采用码型检测的SS-LMS算法，如公式(6)所示，通过外部控制码改变并联电阻的数量，使CTLE能动态地适应不同的信道环境.

图7 本文所使用的连续时间线性均衡器结构Fig.7 Block diagram of the proposed CTLE

2 自适应均衡接收机的设计和实现

2.1 接收器结构

图8（@@@446页）所示为本文提出的自适应均衡接收器结构，主要有3个部分: 组合均衡器部分，包括CTLE、7-tap DFE、DESER(串并转化)以及FSM(有限状态机)等模块，其中基于码型检测的SS-LMS算法实现的DFE FSM和CTLE FSM，用于自适应地控制均衡器；相位插值器(Phase Interpolator, PI)和数据时钟恢复(Clock Data Recovery, CDR)FSM模块，用于为均衡器提供输入信号采样时钟；眼图扫描(Eye Scan)及相关模块，用于检测对接收数据均衡的效果眼图.

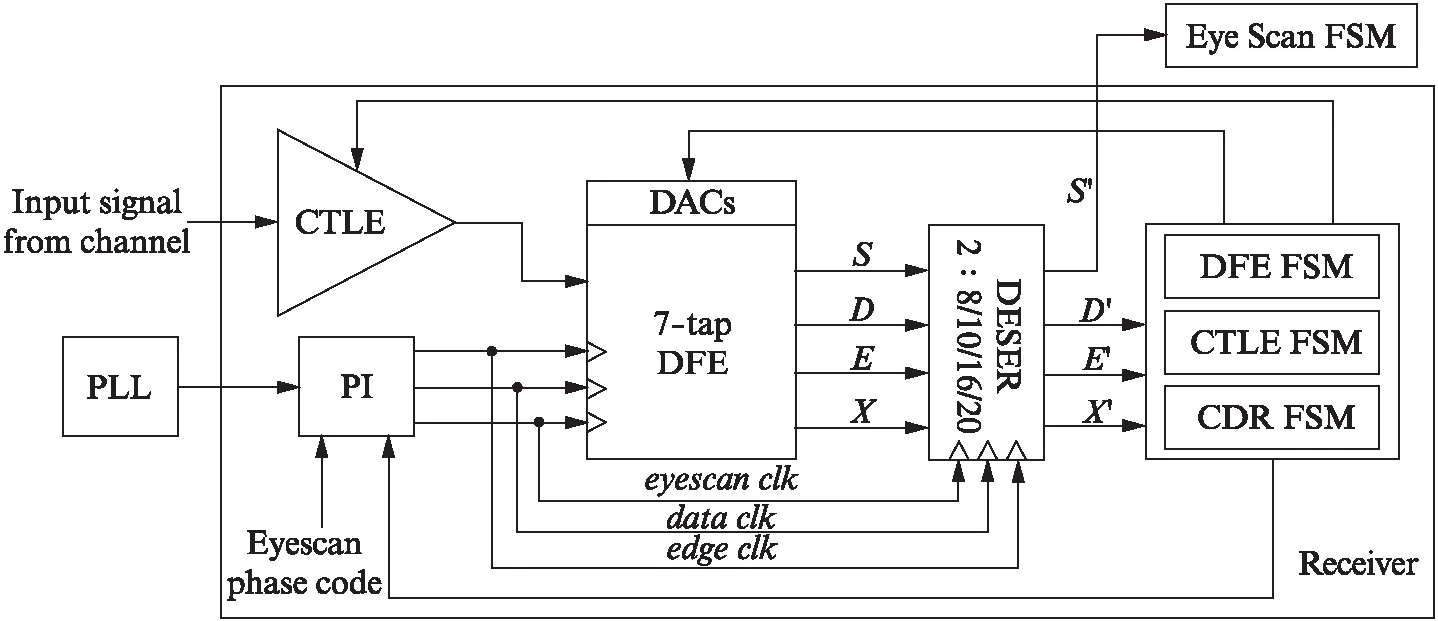
图8 自适应均衡接收器设计框图Fig.8 Diagram of the receiver

图9 接收器中不同时钟相位Fig.9 Different phase clocks in the receiver

输入接收信号首先经过CTLE频域均衡滤波，消除ISI前标分量与长度大于7个UI的后标分量.7-tap DFE接收来自CTLE的信号，通过时域均衡滤波对7个UI内的ISI前标分量进行消除，同时利用PI所产生的不同相位时钟采样得到不同的接收数据(S、D、E、X).本地锁相环(Phase Lock Loop, PLL)产生的四相半波特率时钟输入到PI用于产生DFE的时钟.如图9所示，PI模块在CDR FSM输出的相位码和外部输入的眼图扫描相位码的控制下产生3个不同相位的时钟:data_clk(clk0/clk180)，用于采样每一位串行数据的中央位置得到最终的有效接收数据D和与其相对应的误差数据E，用于SS-LMS计算；edge_clk(clk90/clk270)用于采样每两位数据间的变化边沿，得到接收信号变化沿数据X，用于CDR FSM控制DFE时钟对输入信号的动态跟随；eyescan_clk(sclk0/sclk180)用于采样数据S以检测和统计接收信号经过CTLE+DFE均衡后的眼图宽度，其相位移动由外部输入的眼图扫描相位码来控制.由于本文中DFE所使用的是半速率预处理结构，因此得到的数据信号位宽均为2bits.DFE比较器采样得到的半速率双比特位数据，经DESER串并转换后得到低速并行数据输出S′、D′、E′和X′，通过SRAM配置可以将串行高速数据信号转化为8/10/16/20位宽.最后，在数字模块DFE FSM与CTLE FSM中，采用基于码型检测的SS-LMS算法，使用D′与E′产生DFE抽头系数与基准电压控制码，以及CTLE的并联电阻控制码.DAC阵列将DFE抽头系数与基准电压控制码转化为对应的模拟差分电压，用于DFE中高速接收信号的均衡.CTLE并联电阻控制码用于对CTLE中的负反馈并联电阻数目的控制.通过上述方式，对CTLE+DFE组成的均衡系统进行自适应的参数调节，使接收器可以适应通道与环境的变化.CDR FSM则使用D′和X′产生相位控制码，控制data_clk与edge_clk的相位，跟踪输入信号变化.

2.2 DFE的设计和实现

如图10所示为本文采用半速率预处理结构设计的DFE模块框图，图中所有的信号均为差分信号.图7中，DFE FSM产生的DFE抽头系数控制码DACH1～DACH7与基准电压控制码DACVP在DAC阵列中分别转化为对应抽头的模拟差分电压(VH1～VH7)与输入信号幅度参考电压(VP).在奇偶2路中，第2～7抽头差分电压(VH2～VH7)与对应的前2～7位接收数据(D2_odd～D7_odd/D2_odd～D7_even)相乘，再经模拟加法器(SUM)与输入差分信号(Vin)求和，消除2～7UI的ISI前标分量，得到Vsum_odd与Vsum_even奇偶2路均衡后信号.经过H2～H7抽头均衡后的高速串行信号在奇偶2路被高速比较器(slicer)转化为半速率数字信号，两路的处理模块相同，均采用5个slicer将输入的模拟差分信号采样为数字信号，5个slicer分别是: 用于采样S路数据的眼图扫描比较器，用于采样得到X数据的变化边沿数据比较器，用于采样得到E数据的误差数据比较器，以及2个接收数据比较器用于同时采样分别叠加/减去了差分电压VH1的输入信号.

传统的DFE结构中，由于反馈环路的器件传播延迟限制了数据接收率的提高[12]，为解决这一问题，本文在DFE模块设计中采用了半速率结构和预处理技术，将第1个抽头H1展开以缓解反馈路径的时序限制，通过使用2个接收数据比较器对H1抽头工作进行预处理，在得到同一位接收数据的+VH1与-VH12种不同采样结果后，根据本位数据前一位数据的值选择不同的叠加结果以达到准确的均衡结果.

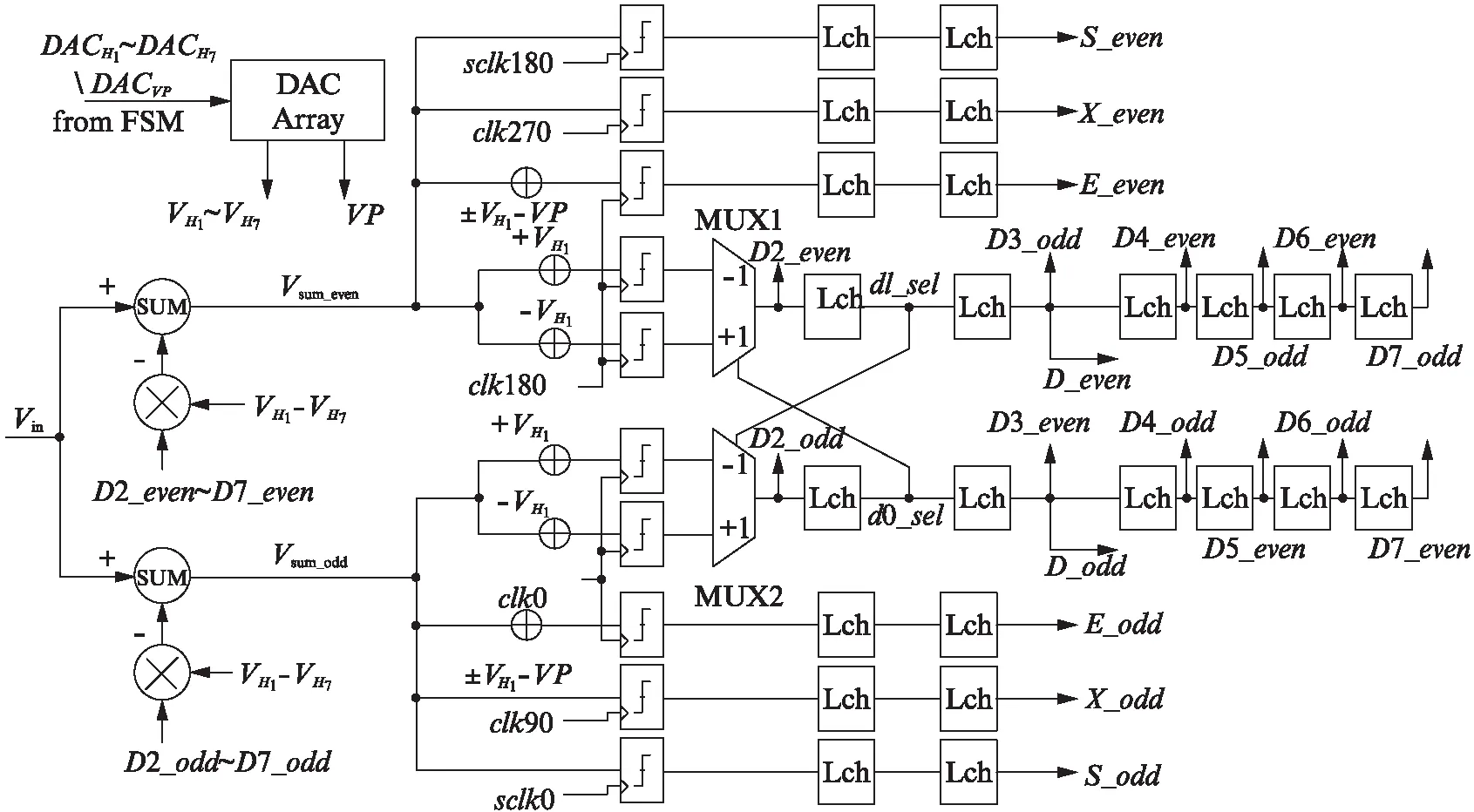
图10 DFE模块框图Fig.10 The block diagram of DFE

在D路的接收数据处理中，对于高速串行信号中每一位数据的第1个抽头的均衡结果都可能有2种情况: +VH1和-VH1.在E路的误差数据处理中，为节省芯片面积与功耗的开销，奇偶2路都只使用了1个误差比较器，用于得到DFE FSM与CTLE FSM所需要的误差数据E.在误差比较器的输入端，+VH1与-VH1由开关时钟(Switch Clk, SWclk)的高低电平轮流进行选通(SWclk的周期可以配置为256～32768时钟分频)，比较器采样得到的误差数据E可以表示为：

(2)

它们分别表示了上一位接收数据值为-1(SWclk=1，高电平)和+1(SWclk=0，低电平)2种情况下得到的当前接收数据位所对应的误差值.误差数据比较器采样得到的误差数据是其输入端信号Vsum±VH1再减去平均幅值电压VP后得到的判决结果，因此在基于码形检测SS-LMS算法对均衡器的控制中，只有接收数据D的本位数据为+1时对应的误差数据才能有效.

2.3 基于码型检测SS-LMS的自适应算法

如图6所示，DESER解串后的D路与E路并行数据被送至CTLE FSM与DFE FSM中，产生CTLE并联电阻控制码与DFE电压控制码，分别用于控制CTLE的零点频率与DFE抽头系数.根据2.2节的分析，接收数据D的控制码型的选择由SWclk与前一位接收数据共同决定.

(1)H2～H7电压控制码的控制码型和抽头系数的迭代计算

图11所示为n时刻时H2抽头电压控制码DACH2的控制码型.由于只有在接收数据D的本位数据d0为+1时对应的误差数据才有效，同时SWclk=0选择本位前一位数据d-1=+1，因此在SWclk=0时D路数据码型选择{d-1，d0}={+1，+1}.在检测出这种码型的前提下，通过比较本位前第2位接收数据d-2与本位误差数据e0的值，并乘以迭代步长μ，得到本次H2抽头系数的修正因子μ·e0·d-2.然后使用SS-LMS的迭代公式计算得到本次迭代计算后的DACH2码值:

DACH2(n+1)=DACH2(n)+μ·e0·d-2.

(3)

同理，当SWclk=1时，选择数据码型时将本位数据与前一位数据的值固定为{d-1，d0}={-1，+1}，并在得到的码型基础上比较d-2与e0得到修正因子并进行迭代计算.DACH3～DACH7的控制码型的选择与抽头系数的迭代计算过程与DACH2相同.

图11 H2抽头的数据码型Fig.11 The data pattern of H2 tap

(2)VP控制码的控制码型与H1系数的迭代计算

根据1.3节所述，改进的SS-LMS算法采用平均差分幅值VP和符号化后的接收数据D的乘积作为近似标准数据，代替标准数据d(n).在本文的DFE电路设计中，由于E路数据是通过SWclk的高/低电平分别控制差分输入信号加/减VH1，因此为有效获得差分电平的平均幅值，将VP电压控制码DACVP分为DACVP0和DACVP12个值，分别用于表示前一位数据为+1或-1时本位数据所对应的输入差分电压的大小.在本文的DFE电路设计中，采用前位数据的码型来分别控制DACVP0和DACVP1的迭代计算.

图12 VP的控制数据码型Fig.12 The data pattern of VP

图12所示为DACVP的数据码型与SWclk之间的关系.当SWclk=0，检测得到的有效数据码型中，本位数据与前1位数据的值被固定为{d-1，d0}={+1，+1}(误差比较器选择输入信号减去VH1).此种情况下，通过比较本位接收数据d0与本位误差数据e0可得到DACVP0的修正因子，并叠加到DACVP0上得到更新码值，此时DACVP1的值保持不变，DACVP选择DACVP0作为输出，其计算如公式(4)所示:

(4)

其中φ是修正因子的步长.同样，当SWclk=1时，选择数据码型{d-1，d0}={-1，+1}，DACVP0保持不变、DACVP1迭代更新并输出.通过这种方式，分别用于表示前一位数据为+1或-1时本位数据所对应的输入差分电压的大小，因此使用DACVP0和DACVP1的差值正好为1UI时间的ISI后标分量大小的2倍，此差值被用于迭代计算H1抽头系数值DACH1:

DACH1(n+1)=DACH1(n)+k·sign[VP0(n)-VP1(n)]，

(5)

其中k为迭代计算的步长.

(3) CTLE的控制码型和系数的迭代计算

CTLE的并联电阻控制码同样使用基于码型检测的SS-LMS算法来自适应控制，控制码型的选择与DFE的H2～H7抽头方式相同，使用符号化后的接收数据D的本位与前一位数据.与DFEH2～H7抽头的区别在于修正因子的计算: CTLE主要用于消除ISI的长拖尾后标分量和前标分量，因此在从接收数据D中得到CTLE的控制码型后，使用本位数据前大于7位(在使用7-tap DFE的情况下)的前位数据与e0进行比较，并将比较得到的结果求和得到控制CTLE参数变化的修正因子，用以控制CTLE的幅频响应.本文的设计中使用了本位前第8位到第20位数据之和来计算得到修正因子，通过此修正因子迭代计算CTLE外部控制码R的值，控制CTLE的退化电阻值及其幅频特性，迭代公式与H2的迭代公式类似:

(6)

其中γ为每次迭代步长.

2.4 DFE & CTLE FSM的设计实现

根据2.3节的讨论，包括DFE的7个抽头系数值、输入信号参考电压以及CTLE负反馈并联电阻系数，所有的均衡器系数迭代变化的过程都分成两个部分: 每次迭代的修正因子的计算，以及系数的累加.因此在对SS-LMS的实现主要分成对应的两部分.图13所示为DFE+CTLE FSM的实现框图.每个系数都对应到VOTE和counter 2个系数控制模块.对并行数据D中的每一位数据，VOTE模块首先检查需要的数据码型，在此码型基础上计算得到在对应增加或减小的指示信号，并求和计算得到每个时钟周期数据的变化步长.例如在第n个抽头系数VOTE模块中，每个时钟周期接收20位宽的并行数据，对20位数据中每一位进行码型检测，检测到6个所需要的数据码型，其中4个计算结果得到e0·d-n值为+1，2个计算结果值为-1，因此在这个周期计算得到的变化步长结果为StepHn=-1×2+1×4=+2，此值使用6位宽的数据表示并送往累加器(counter)输入.在counter中，6位宽的Step首先经过移位器(“<<”)进行算数左移操作，并将其位宽拓展为20位宽，位移数量可配置为0～14来控制SS-LMS公式修正因子中的步长大小.将移位后的步长值存于寄存器中，与上一次迭代计算的均衡器系数结果输入到加法器中得到新的累加结果，新的累加结果存入寄存器中用于下一次迭代计算，同时给到输出移位器(“>>”)中进行逻辑右移，最终高位部分作为均衡控制码被输出到DFE抽头系数DAC阵列中或者是CTLE中.如图13（@@@450页）所示在对DACVP的处理中，使用开关时钟SWclk作为DACVP0和DACVP12个counter模块的控制信号接在使能端，来控制DACVP0和DACVP1分时变化，同时将其输出到H1的比较模块CMP中得到DACH1迭代变化方向并进行累加.

图13 DFE和CTLE FSM结构框图Fig.13 The block diagram of DFE and CTLE FSM

3 测试结果

本文设计和实现的自适应接收器采用TSMC 28nm工艺完成流片，其物理版图如图14（@@@450页）所示，整个接收器的面积为0.55mm×0.40mm=0.22mm2.

图15（@@@450页）所示为本接收器的性能评估测试平台.高速串行的PRBS-7测试序列由误码仪(Bit Error Ratio Tester, BERT)产生，并由BERT调节产生0～-25dB的半波特率衰减来模拟不同类型和长度的背板信道，最后用本文的接收器完成高速串行信号的接收.PC上位机通过RS-232接口与接收测试板连接，用于芯片内部寄存器的配置与监测，以及得到均衡器的眼图扫描信号.

图14 接收器芯片物理版图Fig.14 Photograph of receiver die

图15 性能评估测试平台Fig.15 Performance evaluation platform

实验中，使用BERT分别产生-15dB与-25dB 2种不同半波特率衰减、数据率为12.5Gb/s的高速串行数据序列，分别模拟12.5Gb/s数据通过60cm与90cm 2种不同长度背板金属线的信道衰减.图16(a)所示为经过-15dB信道衰减后的信号眼图，可以看到由于ISI的影响眼图已基本闭合，图16(b)所示为使用本文自适应均衡接收器，在所有均衡器系数收敛后由接收器内部眼图扫描电路得到的均衡后信号眼图.图16(c)所示为经过-25dB信道衰减后的信号眼图，较图16(a)其信号质量更差，图16(d)所示为使用本文自适应均衡接收器得到的信号眼图.图16(b)和图16(d)中经均衡后的信号眼图的垂直眼高与水平眼宽分别达到了105mV/0.6UI与40mV/0.4UI，同时收敛后的数据接收误码率均在10-12以下，表明本文改进和设计实现的自适应均衡接收器可以很好地自适应于0～-25dB的多种不同衰减程度的信道，实现12.5Gb/s高速数据的自适应均衡接收.

图16 不同信道衰减后以及均衡后的眼图Fig.16 Eye diagrams of signal in different channel loss and equalization

图17给出了接收-25dB信道损耗的12.5Gb/s PRBS-7测试序列，接收器均衡器各个参数随接收数据变化的自适应收敛曲线.图17(a)所示为DFE的H2～H7抽头所对应的DAC码值DACH2～DACH7以及CTLE的均衡码值RCTLE的收敛曲线.图17(b)所示为VPDAC码值DACVP以及DFEH1抽头系数DACH1的收敛曲线.可以看到所有的系数值收敛并稳定，一共使用了2×105UI个数据.收敛后，测量得到的误码率小于10-12.

图17 均衡器系数收敛曲线Fig.17 Measured convergence curve of equalizer coefficients

表1给出了本文设计的自适应均衡接收器与其他高速接收器模块的比较.可以看到，在工艺接近的情况下，本文接收器与文献[14]和文献[15]相比，最高数据接收率更高；同时，本文基于码型检测SS-LMS算法实现的自适应均衡器在接收2×105UI数据内得到了所有系数的收敛，相较文献[11]在收敛速度上有明显的提升.

表1 接收器性能比较

a仅包含DFE均衡器部分；b包含发送端的均衡在内.

4 结 语

本文提出了一种基于码型检测SS-LMS算法自适应匹配和调整均衡器参数的新型高速串行接收器设计，采用CTLE和DFE均衡滤波器的组合设计，通过基于码型检测的SS-LMS自适应算法对DFE的7个抽头系数、输入信号参考电压以及CTLE负反馈并联电阻的自适应动态调节，实现了对信道和传输环境的快速、自适应的动态补偿，有效地消除了ISI的前标分量、后标分量以及长拖尾的后标分量，实现了高速串行数据信号的准确接收.同时，设计中所采用的半速率7抽头的DFE结构，有效地缓解了DFE中关键路径的时序要求，提高了接收器的最高工作频率.本文基于码型检测SS-LMS算法提出和设计实现的高速自适应均衡接收器在TSMC 28nm CMOS工艺下完成流片，芯片测试结果表明，在最高12.5Gb/s串行接收速率下，本文设计和实现的自适应均衡接收器，在半波特率6.25GHz、-25dB信道损耗的条件下，可以在2×105UI内获得均衡器系数的快速收敛和稳定，所有均衡器系数收敛后的接收误码率小于10-12.