一类具有k阶拉普拉斯算子的波动方程整体解的存在性*

王 艳 萍

(宿州学院 数学与统计学院，安徽 宿州 234000)

0 引 言

将考虑如下一类具有k阶拉普拉斯算子的波动方程：

(1)

其中，Ω⊂Rn是具有光滑边界的有界区域，常数ai、α>0，且pi和k满足：

(2)

1 主要引理

为了计算方便，引入下面记号：

另外，记

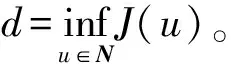
(ii)u(x,0)=u0(x)∈H1(Ω)∩H1,k(Ω),ut(x,0)=u1(x)∈L2(Ω);

Galerkin方法是证明波动方程解的存在性问题最常用的方法之一，为了证明方程(1)弱解的存在性，首先给出下面几个引理。

(3)J(λu)在0≤λ≤λ*上单调增加，在λ*<λ<+∞上单调减少，且在λ=λ*处取最大值;

(4)当0<λ<λ*时，I(λu)>0；当λ*<λ<+∞时，I(λu)<0，且I(λ*u)=0。

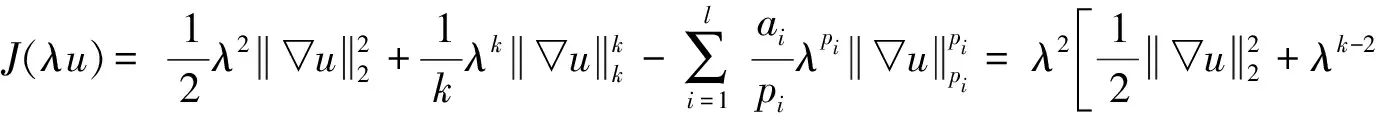
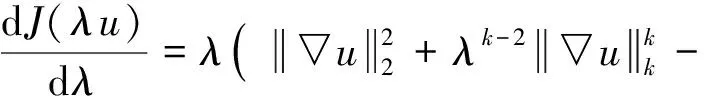
(3)由于

利用h(λ)的性质，可得性质(3)；

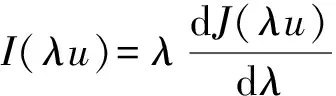
利用文献[4]的方法可得下面引理：

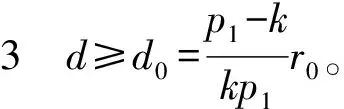
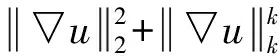
利用文献[7—8]的方法，可以得出：

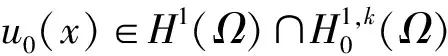
(1) 如果u0∈W′，则方程式(1)—方程式(2)的所有弱解u(x,t)∈W；

(2) 如果u0∈V′，则方程式(1)—方程式(2)的所有弱解u(x,t)∈V。

2 主要结论

下面将利用Galerkin逼近法证明方程式(1)—方程式(2)整体弱解的存在性，方程式(1)—方程式(2)中含有多源项与k阶拉普拉斯算子项，必须采用更加精细的计算，在一定程度上拓展了Galerkin逼近法的应用范围。

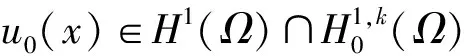
证明设{wj(x)}是特征方程

的一个基础解系，方程式(1)—方程式(2)的Galerkin逼近解可表示为

(3)

从0到t积分可得

利用已知条件，对充分大的l有

(4)

因为u0∈W′，利用文献[8]相同的方法可知，对充分大的l有ul(t)∈W,(0≤t<+∞)。

借助引理3的证明可得：

(5)

从而利用式(4)和式(5)可知，对充分大的l，有

再利用嵌入定理可得，对充分大l，有

令v→+∞，由方程式(3)可得

dτ+(u1(x),wj)+α(u0(x),wj)

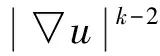
由式(4)得：

从而

所以u为方程式(1)、方程式(2)的一个整体弱解，并利用命题1的u∈W。

3 结束语

讨论了一类同时含有k阶拉普算子项与多个非线性源项的波动方程的初边值问题，这类波动方程改进了含有单个非线性源项的波动方程，由于这类波动方程引入了k阶拉普拉斯算子项和多个非线性源项，使得该波动方程的结构更加精细且符合实际。Galerkin逼近法是证明波动方程解的存在性问题最常用的方法之一，论文应用构造了这类方程的近似解，并讨论了近似解的收敛性，最后得到了整体解的存在性。