江西抚河2010年唱凯堤溃堤洪水模拟反演分析

丁志雄，李 娜，许小华，李德龙

（1.中国水利水电科学研究院，北京 100038； 2.水利部防洪抗旱减灾工程技术研究中心，北京 100038；3.江西省水利科学研究院，江西 南昌 330029）

1 研究背景

河流堤防是抵御洪水侵害的一项重要水利工程设施，堤防一旦发生因洪水导致的漫顶或溃决，其造成的影响或损害可能极其严重，而尤以堤防溃决造成的灾害更具有突发性和不可预测性。为了减轻溃堤洪水的灾害影响，除了转移受灾群众和重要财物外，往往会采取及时、快速封堵修复或排水的防洪抢险措施。近年来，国内外许多学者研究了溃堤洪水的数值模拟，其主要是利用二维水动力模型模拟溃堤洪水在二维平面上的演进情况［1-6］。然而，对于溃堤发生后可能的采取封堵修复或排水的抢险措施考虑的情况少。本文利用适用性较宽泛的二维非恒定流完全圣维南方程组建立溃堤洪水模型，并利用基于共轭单元离散的有限体积法进行模型求解。以江西抚河2010年唱凯堤溃堤洪水为例，考虑当时实际的溃堤封堵修复过程和溃堤分流的实际情况，进行溃堤洪水的模拟反演，并与现场采集的实际洪痕进行对比验证，以期为溃堤洪水的防洪抢险提供参考和借鉴。

2 区域概况

唱凯堤位于江西省第二大河抚河的中下游右岸，抚州市临川区东北部，涉及湖南、罗湖、唱凯、罗针、云山5个乡（镇），为一条封闭圩堤，圩堤全长81.8 km，保护耕地0.93万hm2，保护人口19.9万人。

2010年6月抚河发生大洪水，全线超警戒水位。6月21日18时30分，唱凯堤在灵山何家段（桩号32+923～33+270）发生决口（以下简称“何家段溃口”），起初溃口宽度5 m，后迅速发展到60 m，到6月22日7时30分溃口宽度扩至347 m，2010年6月22日上午拍摄的溃口处照片如图1所示［7］，图中标识了溃口宽和溃口入流方向。堤防溃决造成受灾乡镇4个、受灾村41个，被淹区平均水深2.5 m至4 m，其中罗针镇、唱凯镇受灾最严重，整个受淹区域人口约10万人。

2010年6月23日6时30分左右，江西抚州唱凯堤内的洪水在罗针镇长湖村附近再次冲开一个新缺口（以下简称“长湖村溃口”），缺口宽度约150 m。洪水一部分泄入抚河，一部分倒灌东乡河。同时6月23日武警水电部队开始进行灵山何家段溃口的封堵，至6月27日18时灵山何家段溃口胜利合龙［8］。因此6月27日18时后，唱凯圩堤内何家段溃口不再有水量流入。

唱凯堤溃堤洪水具有一定的代表性，首先堤防溃决具有较长的发展过程；其次溃决后有人工堵口修复工作的介入；还有下游自然冲开堤防进行洪水排出等现象的发生。因此研究清楚溃堤洪水的发展演进过程，人工堵口修复对洪水的影响及其保护区进水后的排水输干等问题，对于堤防溃决后的防洪、抢险、救灾以及灾后恢复重建等都具有非常重要的参考价值。

图1 唱凯堤灵山何家决口处实拍照片（2010年6月22日上午拍摄）

3 溃堤洪水模拟模型及其求解算法

3.1 溃堤洪水模拟模型中国水利水电科学研究院于1990年代开发了一套基于水动力学的二维洪水模拟仿真模型（IWHR-FRAS）［9］，该模型主要采用扩散波方程对洪水进行模拟演算，模型较好地适用于城市的暴雨内涝及较小区域的溃堤洪水模拟，近年来结合全国重点地区洪水风险图的编制，对该模型作了进一步的改进，针对大范围的溃堤洪水模拟，模型采用适用性较宽泛的二维非恒定流的完全圣维南方程组，考虑了水流的惯性项和摩阻项，具体如下：

质量守恒方程（连续方程）：

动量守恒方程（运动方程）：

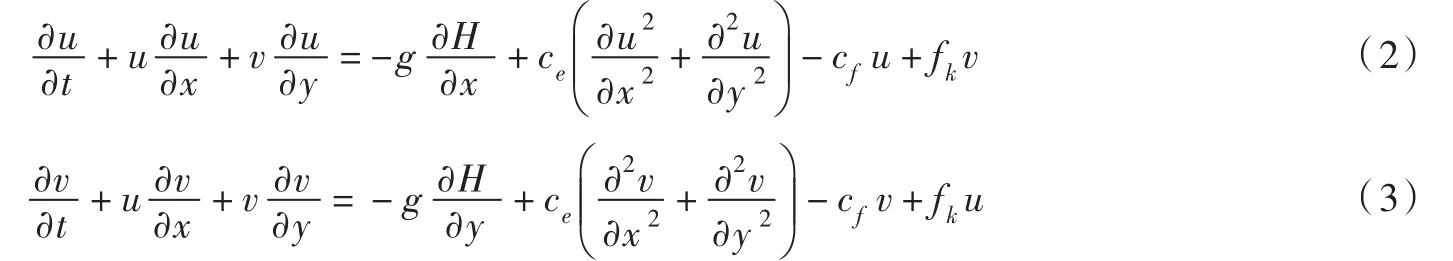
式中：H为水位；h为水深；u、v分别为流速在x、y方向的分量；t为时刻；q为源汇项；g为重力加速度；ce为涡黏系数；cf为摩阻系数，由曼宁糙率确定；fk为科氏力系数。

3.2 模型求解算法二维非恒定流圣维南方程的数值求解方法主要有有限差分法（Finite Difference Method，FDM）、有限单元法（Finite Element Method，FEM）以及有限体积法（Finite Volume Method，FVM）等。有限体积法是近年来兴起的一种用于不可压缩流体计算的数值求解方法，由于该方法从物理规律出发，每一离散方程都是有限大小体积上的某物理量的守恒表达式，在推导过程中物理概念清晰，并可以保证离散方程的守恒性，同时该方法能像有限单元法一样适用于不规则网格和复杂边界情况，但处理效率要远高于有限单元法，所以在当今流体力学数值模拟计算中有着越来越广泛的应用。这里主要利用基于共轭单元离散的有限体积法进行溃堤洪水的完全圣维南方程组的求解，共轭离散单元如图2所示，共轭单元及节点不是真实存在的，由离散网格单元根据单元的共轭关系自动计算得到，用于辅助计算离散网格单元的水位和流量。

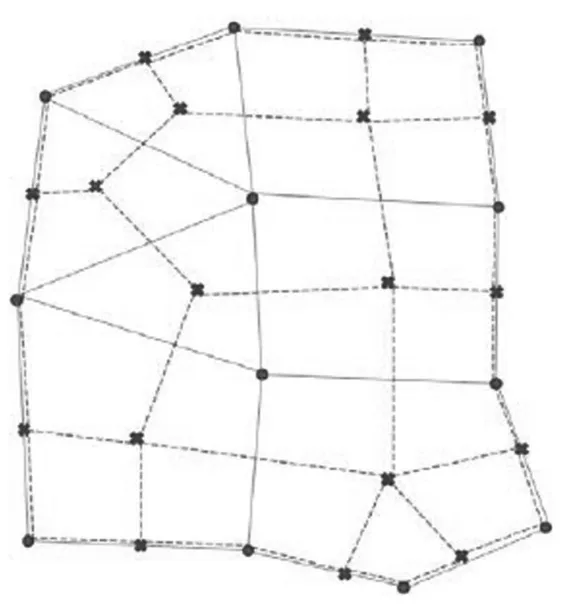
图2 共轭离散单元示例(实线和圆点为离散单元和节点，虚线和方点为共轭单元及节点)

将上述完全圣维南方程组的连续方程写为矢量形式如下［4］：

式中：V=（u，v）为流速矢量；为偏微分算子。

运动方程的矢量形式如下：

根据高斯散度定理，单元的通量与单元水体体积的变化保持恒定［5］。对于连续方程（式（4））在空间共轭离散以及时间离散后每个单元的水量近似满足如下关系式：

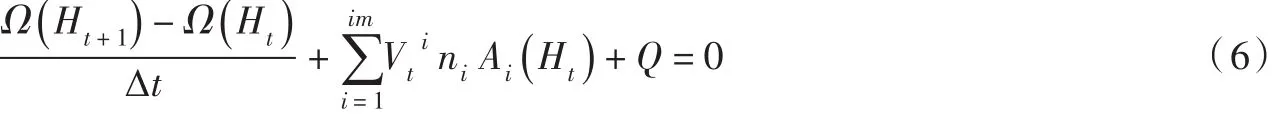
式中：Ω（H）为单元不同水位下的水体体积，由单元形态特征计算成水位-水体体积关系查算表；im为离散单元的边数；ni第i边元（单元的一条边）的法向量；Ai（Ht）为第i边元的过水面积，由边元形态特征计算成水位-过水面积关系查算表；Q为区域降雨、蒸发或入渗量。

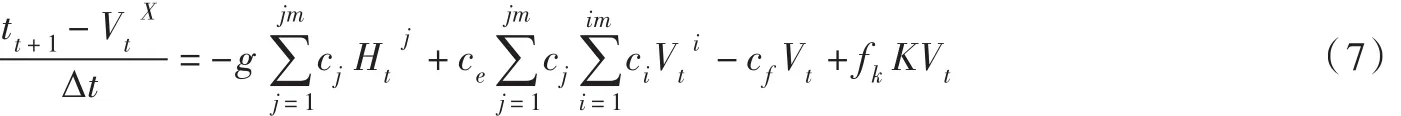
对于运动方程（式（5）），在空间共轭离散以及时间离散后每个节点流速近似满足如下关系式［6］：式中：由广义重心坐标插值得到，包括流速大小和方向；jm为节点相关单元个数；cj为节点第j个相关单元与所在共轭网格单元形状关系系数；ci为节点第j个相关单元所有节点的相关单元与所在共轭网格单元形状关系系数。

在设定边界及初始条件下，得到每个网格的水位及每个节点（每个节点对应一个边元）的流速vt及Ht，从而由式（6）、式（7）可以联立求解得到vt+1及Ht+1，并能够保证在每个离散网格和时间步长上水流的近似质量守恒和近似动量守恒。

4 唱凯堤溃堤洪水模拟模型建立

唱凯堤洪水分析模型的模拟计算面积为86.51 km2，概化分为14 130个不规则网格，如图3所示。其中，包括边元数28 240条、节点数14 758个。在网格剖分过程中，以唱凯堤圩区的计算范围作为边界约束条件，将京福高速公路、316国道等阻水建筑物作为内部约束条件，并以每个网格面积不超过0.05 km2为标准进行网格剖分，对于特殊地形地物，如高速公路等进行了局部加密处理。网格的糙率按土地利用类型进行糙率取值，每个网格可能包含多种土地利用类型，则用面积加权平均进行求取网格的糙率。

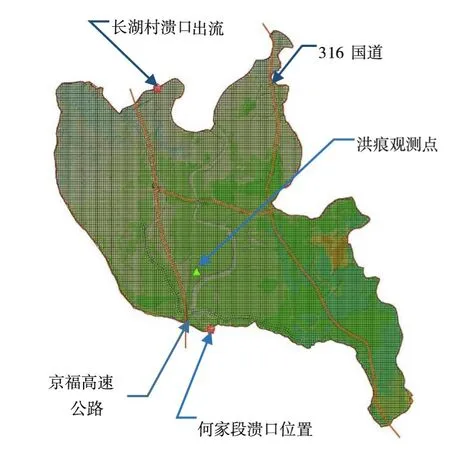
图3 唱凯堤溃决模拟分析二维模型

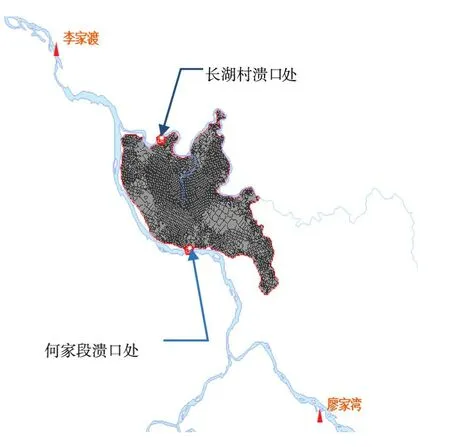
图4 唱凯堤溃口及抚河上下游水文站位置

5 唱凯堤溃堤洪水的模拟反演及结果分析

5.1 溃堤洪水模拟反演唱凯堤溃堤洪水计算主要考虑堤防溃决的发展过程以及何家段溃口的修复过程，溃口处采用水位边界，模拟时间步长为10 s。

（1）溃口发展过程。根据唱凯堤灵山何家段2010年洪水实际溃决情况，2010年6月21日18时30分发生溃决，初始溃口宽度为5 m，最终溃口宽度为347 m，溃口发展历时约13 h。建立溃口的线性发展方程如下：

式中：Y为溃口宽度；a为溃口初始宽度（5 m）；X为溃口历时，min。

随着唱凯堤地内蓄水量的增加6月23日6时30分左右唱凯堤罗针镇长湖村发生溃决，溃口宽度约150 m，溃口历时约5 h，因此建立溃口的线性发展方程如下：

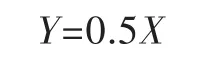
式中：Y为溃口宽度；X为溃口历时，min。

（2）溃口处水位。唱凯圩堤溃口位置位于抚河的廖家湾水文站和李家渡水文站之间（如图4）。2010年6月唱凯堤发生溃决洪水时，这两个水文站均有较详细的水位记录，该水位资料全面反映了唱凯堤溃口上下游水位的变化过程，因此可以用这两个站点的实测水位资料，按距离的线性关系插值计算出唱凯堤溃口处的水位，作为模型的水位边界输入。

（3）何家段溃口的修复过程。2010年6月23日武警水电部队奉命封堵灵山何家段决口，至6月27日18时灵山何家段决口胜利合龙，因此何家段溃口的修复从溃口完成后约24 h开始，溃口修复经历的时间为107 h，建立何家段溃口开始修复后的宽度变化方程如下：

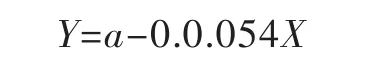
式中：Y为开始修复后的溃口宽度；a为溃口宽度（347 m）；X为溃口修复历时，min。

5.2 反演结果分析

（1）溃口处入流过程。模型计算的唱凯堤何家段溃决入流流量变化过程如图5示，由图可见溃口处入流流量在溃口发生后约10 h内迅速增加，最大达到1544.475m3/s。最初溃口流量迅速增加的过程与实际溃口的发展过程基本一致。从何家段溃口处堤内外水位变化过程看（图6），溃口发生后，堤外水位一直均高于堤内水位，直至6月27日以后堤外水位才降低到比堤内水位低，与该溃口处的完成封堵时间基本一致。

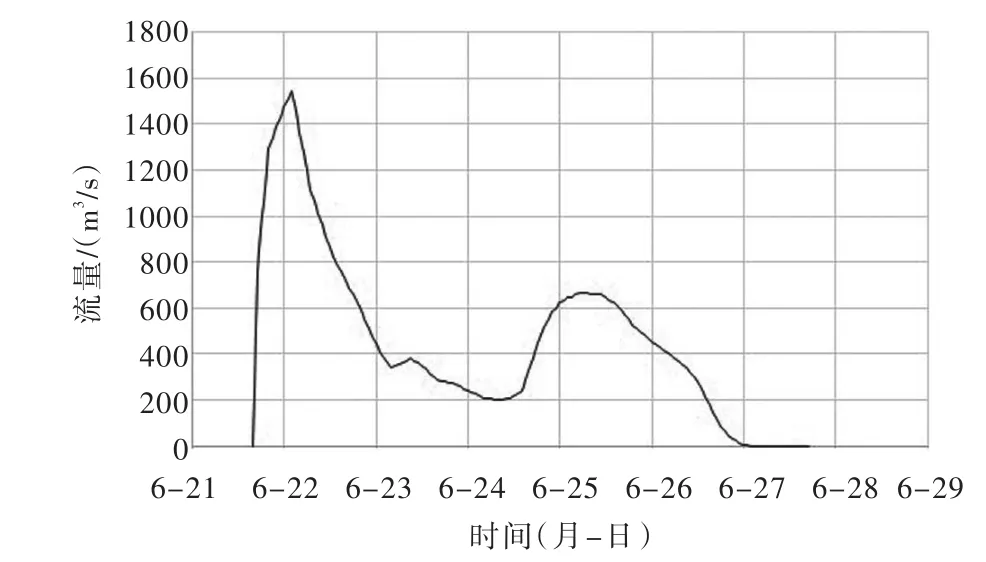
图5 何家段溃口处入流流量过程

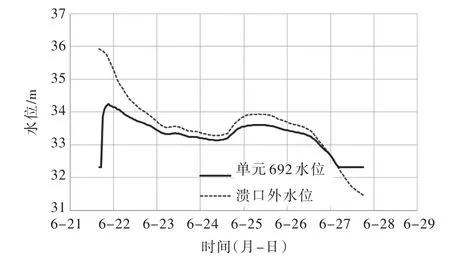
图6 何家段溃口处堤内外水位变化过程

（2）出口流量过程。模型计算的唱凯堤长湖村溃决出流流量变化过程如图7所示，由图可见长湖村溃口处出流流量在6月23日6时发生溃决后，出流流量逐渐增加，变化趋势与长湖村溃口处堤内外水位的变化过程基本一致（图8）。

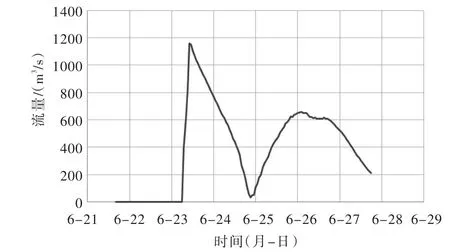
图7 长湖村溃口处出流流量变化过程

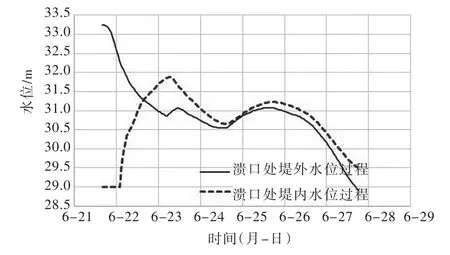
图8 长湖村溃口处堤内外水位变化过程

同时由图8可以看到，长湖村溃口处堤内（模型网格编号565）在何家段溃堤后最初8小时还没有水，8 h后何家段溃堤洪水到达，水位逐渐增加，但仍低于长湖村溃口处堤外水位（东乡河水位）；到6月22日15时，长湖村溃口处堤内外水位持平，达31.31 m；6月23日6时30分长湖村溃口，此时长湖村堤内外水位差0.96 m，唱凯堤圩区洪水通过该溃口直接泄入东乡河直至排入抚河。

随着长湖村溃口的发生，圩区内水位逐渐降低，到6月24日23时长湖村溃口处水位基本要接近堤外（东乡河）水位，但由于后续洪峰的到来，何家段溃口入流量的增加，长湖村溃口处堤内外水位差又有所增加，可见模型基本反映了溃口的入流、出流以及圩区内的水位变化情况。

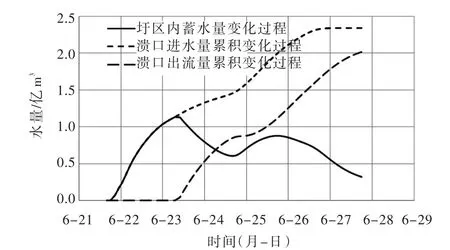
图9 圩区内进出水量及区内剩余水量变化过程曲线

图10 洪痕观测点模型计算水深变化过程

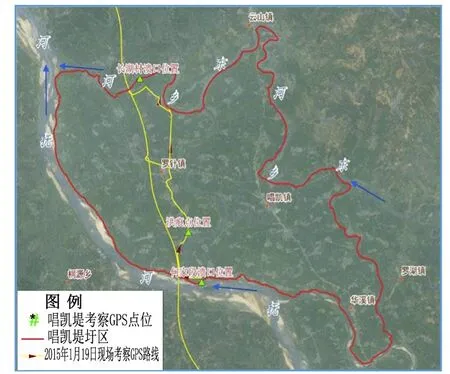
图11 现场考察GPS记录路线图及考察点位

图12 洪痕水深现场照片

（3）唱凯堤圩区内进出水量变化过程分析。唱凯堤圩区自何家段溃堤开始至6月27日18时完成何家段溃堤的封堵，由模型计算得圩区内的进出累积水量及区内蓄水量的变化过程如图9所示。由图9可见唱凯堤圩区内自6月21日16时何家段溃决开始，总进水量持续增加，到6月27日达到2.34亿m3；圩区内自6月23日6时长湖村溃决开始由圩区排出的水量也持续增加，到6月27日18时外排水量达到2.02亿m3；唱凯堤圩区内蓄水量自6月21日16时何家段溃决开始水量持续增加，在6月23日6时以前蓄水量增加较快，6月23日6时以后受长湖村溃决自然排水影响，唱凯堤圩区内蓄水量增加逐渐放缓，到6月23日7时，唱凯堤圩区内蓄水量达到最大，为1.14亿m3，之后圩区内蓄水量开始减小，到6月27日18时圩区内蓄水量减小到0.32亿m3。由于长湖村溃口处地面高程约为28.35 m，圩区内大部分区域均高于该高程，因此圩区内的水均可通过该溃口自然排干。

图13 溃堤后洪水模拟演进不同时刻淹没范围变化

（4）洪痕点水深变化过程。2015年1月19日到唱凯堤现场进行了考察，察看了2010年洪水的何家段溃口位置、长湖村溃口位置以及仍保留有2010年堤防溃决洪水时的洪痕位置（对应模型网格编号6644）。模型计算洪痕处的水深变化过程如图10所示。从图可见，何家段溃口发生后约1个小时，洪水到达洪痕观测点，并且水深迅速增加到最大水深1.85 m左右。

现场考察行进GPS记录的路线及考察点位如图11所示。洪痕位置的水深淹没状况如现场照片图12所示，从现场实测对比可见，最高洪痕处距地面约1.95 m。可见模型计算结果与现场考察观测到的洪痕水深非常接近，误差约为0.1 m。

（5）淹没范围变化过程。根据唱凯堤溃决洪水模拟演进计算结果，绘制不同时刻的洪水淹没范围及水深分布如图13。由图可见溃决发生后12 h（2010年6月22日4时），唱凯堤圩区内大部分区域已被淹，演进48 h（2010年6月22日16时）后唱凯堤圩区内淹没范围进一步扩大，洪水演进到第72 h（2010年6月23日16时）受长湖村所在圩堤段溃决（2010年6月23日6时）影响，唱凯堤圩区内淹没范围已经有所减少，洪水演进到第144 h（2010年6月27日18时），受何家段溃决口门的封堵成功以及长湖村所在圩堤溃决的自然排水，圩区内淹没范围已大大减少。

6 结论

2010年6月江西抚河唱凯堤溃决洪水是近年来发生的一次较大的溃堤洪水灾害，洪水影响人口十多万人，溃堤有较长的发展过程，溃堤发生后既有人工修复的介入，又有堤防自然溃决排水过程的发生，因此该堤防溃决具有较突出的典型性。

利用改进的中国水利水电科学研究院洪涝仿真模型（IWHR-FRAS），针对溃堤洪水建立了模拟唱凯堤溃堤洪水的数学模型，进行了溃堤及洪水发展过程的模拟反演。结合溃堤后现场考察的实测资料，对模型反演结果进行了分析，结果表明：所建立的唱凯堤溃堤洪水模拟模型可以较好地模拟反演溃堤、修复及排水等因素影响下洪水的发展变化过程；计算的溃口流量过程与堤内外的水位变化过程相一致；溃堤后唱凯堤保护区内的水量变化过程及淹没范围变化比较合理，与实际情况也相吻合；计算的洪痕处的水深与现场观测的洪痕水深比较接近，误差只有10 cm，符合洪水模拟的一般技术规范要求。因此利用该模型，建立溃堤洪水的实时模拟分析系统，结合人工修复干预下的实时溃堤洪水进行模拟演算，则可以为溃堤发生后的防洪、抢险、救灾等工作的开展提供重要的技术参考。