全国小流域分布式单位线综合分析

郭 良 ，翟晓燕 ，刘荣华 ，李照会

（1.中国水利水电科学研究院，北京 100038；2.水利部防洪抗旱减灾工程技术研究中心，北京 100038）

1 研究背景

单位线技术是应用水文学最有效的工具，方法应用简便、计算效率高［1-2］，已广泛用于我国流域水文预报、水利工程设计等［3-4］。然而，流域降雨径流过程实质上是一个复杂的水文非线性系统，传统单位线法一般将其概化为线性时不变系统［5-6］，忽略了净雨空间分布和下垫面空间异质性的影响，此外，单位线汇流参数的确定大多依赖于实测暴雨洪水资料，限制了其在缺资料地区中小流域的应用。流域地形地貌特征与降雨特性是影响小流域暴雨洪水过程的主要因子［7］，Maidment等［8］和郭良等［9-11］基于数字高程模型探索流域水文响应与地形地貌、雨强间的非线性定量关系，提出了分布式单位线法，认为流域内各点汇流时间的概率密度分布等价于瞬时单位线，实现了缺资料地区汇流计算，为缺资料地区山洪预报预警提供了技术支撑。

我国中小流域暴雨洪水暴涨暴落、突发性强、历时短，洪水预警期较短，开展分布式单位线综合分析，有助于实现缺资料地区山洪的早期快速预报预警。近年来，“3S”技术的发展促进了流域地形地貌特征的高效准确获取，为辨识流域属性对小流域汇流过程的定量影响提供了数据基础［12］。流域地形地貌属性一般可分为线性尺度测量指标和无因次特性指标两类［13］，常用于缺资料地区流域单位线综合分析和汇流计算。已有研究中采用的流域属性指标多为流域面积、沟道长度、流域坡降等参数，未考虑流域内部地形地貌空间分布异质性对汇流过程的影响，导致设计洪水估算不合理、洪水预报预警精准度低等问题［14-16］。因此，需要进一步挖掘能定量描述小流域地形地貌空间差异的属性参数，构建具有汇流成因的单位线综合公式，提高缺资料地区中小流域洪水预报预警的精准度和时效性。本研究期望为缺资料地区中小流域暴雨洪水分析计算提供技术参考。

2 全国小流域数据集

2010年以来，中国水利水电科学研究院结合全国山洪灾害防治项目，基于1∶5万数字高程模型、2.5 m分辨率数字正影像图、1∶5万数字线划图等高精度国家基础地理空间信息，构建了大范围小流域精细划分和属性分析技术体系，将全国划分为53万个小流域（平均面积16 km2）和378万条沟道河流，形成了全国小流域数据集［9］，覆盖国土面积868.67万km2，为全国山洪灾害防御提供了海量基础数据，为不同自然地理格局下暴雨山洪关键因子辨识量化提供依据，实现缺资料地区洪水预报预警。全国小流域数据集主要包括53万个小流域的75项主要基础属性和分布式单位线组等。

2.1 小流域基础属性小流域基础属性包括反映小流域形状、坡度、高程、汇流路径长度等常用属性，如小流域面积、周长、形状系数、平均坡度、最长汇流路径长度及其比降、沟河长度及平均比降等。通过分析小流域内部高程、汇流路径长度与集水面积间的关系，提出了小流域不均匀系数、加权平均坡度等反映小流域汇流非均质性的参数。

小流域平均汇流路径长度为小流域内水滴由各网格点汇流至小流域出口的汇流路径平均值。以小流域平均汇流路径长度与最长汇流路径长度一半的比值，反映小流域内水流流路分布的非均质性，即小流域不均匀系数，计算公式如下：

式中：L为小流域平均汇流路径长度；Lm为小流域最长汇流路径长度；C为小流域不均匀系数。

对于小流域坡面而言，以各网格点上游集水面积占所有网格点集水面积之和的比例作为权重，基于各点坡度计算小流域加权平均坡度。加权平均坡度通过小流域内各点集水面积的空间分布反映小流域内地形分布对水流汇集的影响，平均坡度反映了小流域地形的平均起伏状态对水流汇集的影响。

式中：S′为小流域加权平均坡度；Sj为小流域坡面网格点j的坡度；ij为坡面网格点j的集水面积；n为小流域坡面网格数。

全国小流域不均匀系数和加权平均坡度频数分布如图1所示。全国26.4%的小流域内各点汇流路径分布趋于均匀分布，小流域流路质心与形心基本重合，小流域形状呈上下游对称（|C-1|≤0.05）；73.6%的小流域流路分布较不均匀，其中，9.7%的小流域流路质心偏下游，水流汇集路径较短，较易形成山洪（C＜0.95），63.9%的小流域流路质心偏上游，水流汇集路径较长，洪水集中偏慢（C＞1.05）。以加权平均坡度与平均坡度之差进一步反映小流域坡度的非均质分布特性。全国约半数小流域坡面上、下游坡度分布较为一致（|S′-S|≤0.05）；约34.5%的小流域坡面上游地势陡峭、下游地势平缓，小流域坡面侧剖面多呈“凹”型分布（S′-S＜-0.05），坡面的侵蚀强度较大，易于形成山洪滑坡地质灾害；其余小流域侧剖面多呈“凸”型分布（S′-S＞0.05），坡面有利于排水，但水流冲刷作用也较强，容易造成水土流失问题。

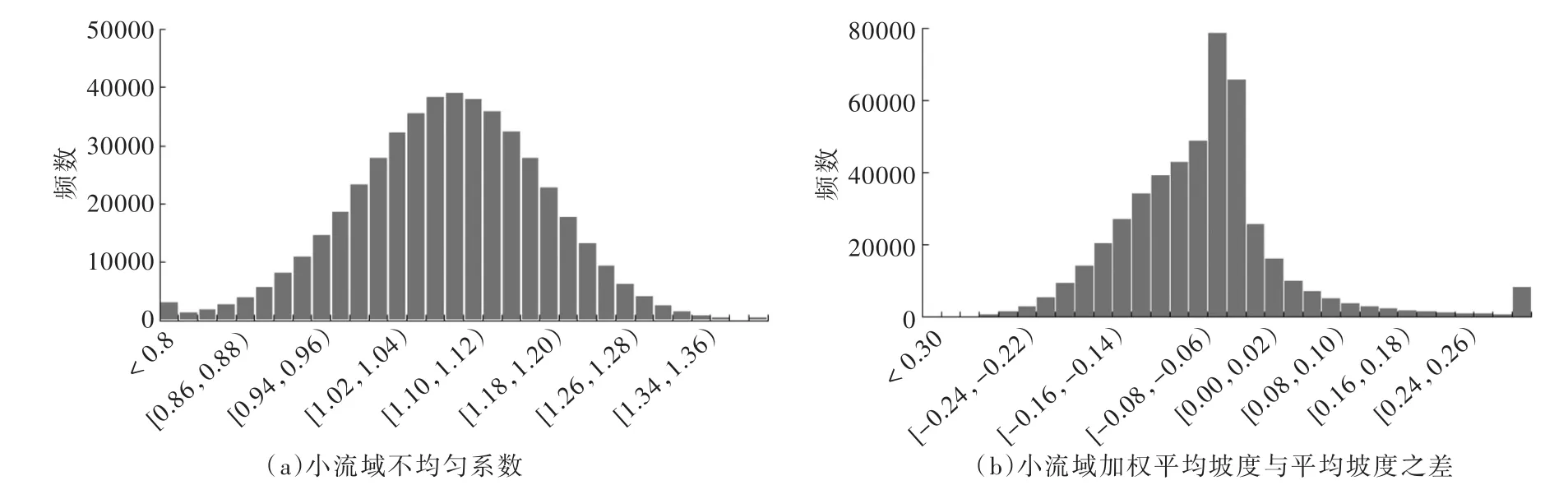
图1 全国小流域不均匀系数及加权平均坡度频数分布

2.2 分布式单位线应用1∶5万DEM和2.5 m土地利用和植被类型信息数据，充分考虑流域下垫面空间分布异质性，提出基于DEM网格、考虑雨强影响汇流非线性特征的分布式单位线方法。在全国范围内共提取了53万个小流域15组不同雨强（5～100 mm/h）、不同时段（10～60 min）的分布式单位线组，使用不同地貌类型区361个流域1万多场暴雨洪水资料进行检验，93.4%的流域雨洪模拟精度较高（即洪峰流量相对误差不超过20%，峰现时间误差不超过2 h），并已用于全国不同类型区中小流域洪水模拟及预报预警［9，17-19］。

坡面流流速计算采用改进的SCS流速公式，综合考虑雨强、坡面地形对流域汇流非线性的影响。基于D8算法，统计流域各网格（25 m×25 m）的径流汇集路径及时间，如公式（3）所示。统计流域内各网格的汇流时间场，得到流域汇流时间的概率密度分布和累计S曲线，进一步考虑流域的调蓄作用，即可得到小流域非线性分布式汇流单位线。

式中：V为水流速度；K为流速系数，主要反映土地利用特征对流速摩阻影响的经验参数；S为流域内某网格沿着水流方向的坡降；i为无因次雨强；Tj为第j个网格的汇流时间；Lk为第k个网格的流路长度；c为系数，c=1或为第j个网格汇流路径上网格的数量。

以降雨量30 mm、时段长10 min的单位线为例（图2），除去湖泊、沼泽和水库外，全国小流域单位洪峰模数处于0.01～0.51 m3/（s·km2）之间，平均值为0.26 m3/（s·km2），四分位数为0.18 m3/（s·km2）和0.33 m3/（s·km2）；全国小流域汇流时间处于0.5～2.0 h之间，平均值为1.09 h，四分位数为0.83 h和1.33 h。各小流域差异明显，成果直观反映了不同地区小流域下垫面条件对洪水集中度和洪水汇集时间的影响。

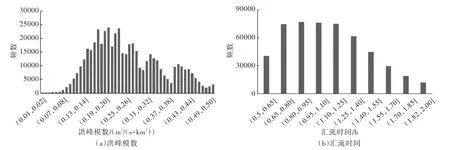
图2 全国小流域单位线洪峰模数、汇流时间频数分布

2.3 典型流域在全国选取30个典型中小流域共4610个小流域作为研究区，其基本信息如表1所示。典型流域面积为755～5874 km2，平均流域面积为2275 km2，分别包括44～406个小流域，研究区跨越三大阶梯，在高原、山地、丘陵、盆地和平原均有分布，地形地貌差异较大，平均高程为128～5017 m，相对高差为528～3327 m，平均坡度为0.05～0.65；研究区分布在19个水文亚区，涉及丰平枯水带及多种水文情势特征；水系发育程度不一，对径流的调蓄能力不一，河网密度为0.25～0.41 km/km2，河网频度为0.02～0.03条/km2，发育系数为2.32～21.16，水系不均匀系数为0.05～2.99。典型流域反映了我国自然地理空间特征的复杂性及差异性，部分典型流域的地形、水系和小流域分布如图3所示。

图3 部分典型流域地形、水系及小流域分布

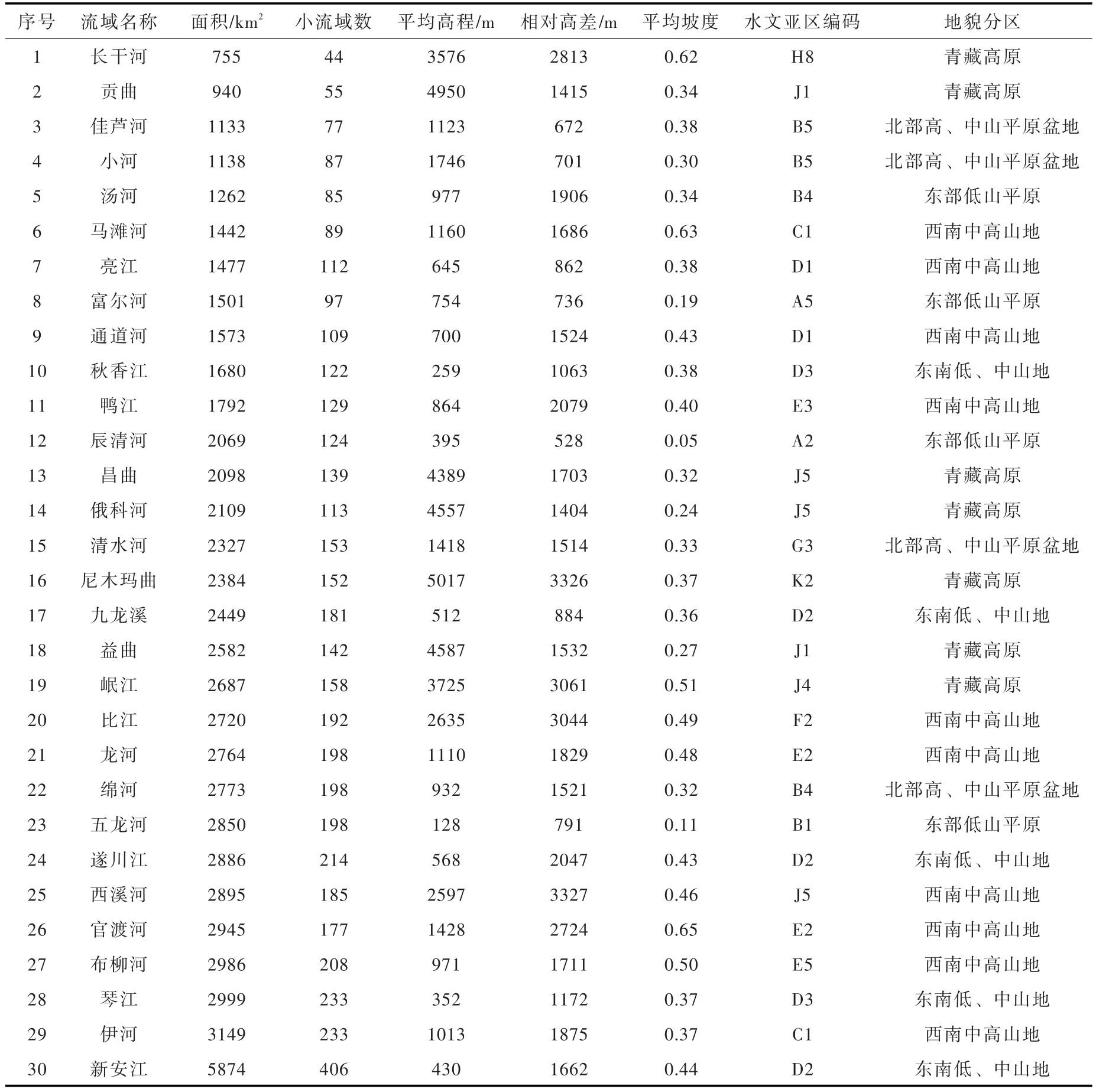
表1 典型流域基本信息统计

3 典型流域单位线公式优选方法

采用Pearson相关系数（r）分析流域属性与单位线特征值（即洪峰流量、汇流时间和峰现时间）之间的线性相关性，以|r|在0.2～0.5之间为中度相关，以|r|≥0.5为强相关。对相关系数进行显著性检验，原假设（H0）为：r=0，显著性检验的统计值服从自由度为n-2的T分布。检验统计量计算公式为：

式中：t为统计量；r为相关系数；n为样本数；检验的显著性水平α取为0.01，若计算统计量的显著性水平p＜0.01，则拒绝原假设，说明流域属性与单位线特征值间存在显著的线性相关性。

我国中小流域产汇流非线性特质十分显著，采用基于最小二乘法的多元回归非线性模型识别分布式单位线特征值与小流域属性间的定量关系。回归模型的一般形式如下：

式中：X为小流域单位线的特征值，如单位线洪峰流量、汇流时间和峰现时间；M为小流域属性，如小流域面积、坡度、汇流路径长度等；i为所选小流域属性个数；k和n分别为拟合系数和拟合指数。

优选最佳拟合公式型的目标函数为均方根误差（RMSE）最小，采用合格率（ST）和相关系数（r）进一步评估拟合公式的优劣。RMSE、ST和r的最优值分别为0、100%和1，各评估指标计算公式如下：

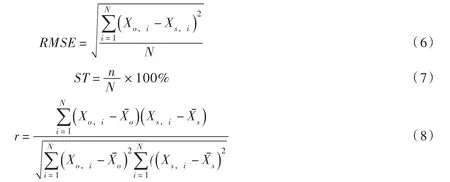
式中：RMSE为均方根误差；ST为合格率；r为相关系数；X为分布式单位线的特征值，如洪峰流量Qm，峰现时间Tp和汇流时间T；N为区域或流域内分布式单位线的总数；n为拟合的单位线特征值合格的分布式单位线数，以单位线特征值的相对误差在±20%以内为合格，即；Xo，i为区域或流域内第i个分布式单位线的特征值；Xs，i为区域或流域内第i个分布式单位线的拟合特征值；Xˉo和Xˉs分别为区域或流域内分布式单位线特征值和拟合特征值的均值。

4 相关性分析及结果评估

4.1 相关性分析小流域汇流过程受降雨特性影响较大，不同降雨强度下单位线过程变化显著，本文主要以雨量为30 mm、时段长为10 min的分布式单位线为例进行单位线综合分析。结合小流域汇流特性分析，选取的小流域属性包括小流域面积A、最长汇流路径长度Lm及其比降J、平均汇流路径长度L、加权平均坡度S′、平均坡度S、河段比降Jr等。部分典型流域小流域属性与单位线特征值间的相关系数绝对值分布如图4所示。对于小流域单位线洪峰流量而言，其与所有典型流域小流域面积的正相关性均较强（0.70≤r≤0.95，p＜0.01），与所有典型流域小流域平均/最长汇流路径长度均存在中度～强度正相关关系（0.22≤r≤0.86，p＜0.01），与37%～73%的典型流域小流域最长汇流路径比降、加权平均比降、平均比降、河段比降存在中度正相关关系（0.20≤r＜0.50，p＜0.01）。对于小流域单位线汇流时间而言，其与所有典型流域小流域平均/最长汇流路径长度的正相关性均较强（0.81≤r≤0.98，p＜0.01），与所有典型流域小流域最长汇流路径比降均存在中度负相关关系（-0.81≤r≤-0.23，p＜0.01），与17%～25%的典型流域小流域加权平均比降、平均比降、河段比降存在中度负相关关系（-0.50＜r≤-0.20，p＜0.01），此外，小流域单位线汇流时间与洪峰流量之间存在中度正相关关系（0.20≤r≤0.64，p＜0.01）。小流域单位线峰现时间与小流域属性间的相关关系与小流域单位线汇流时间类似。

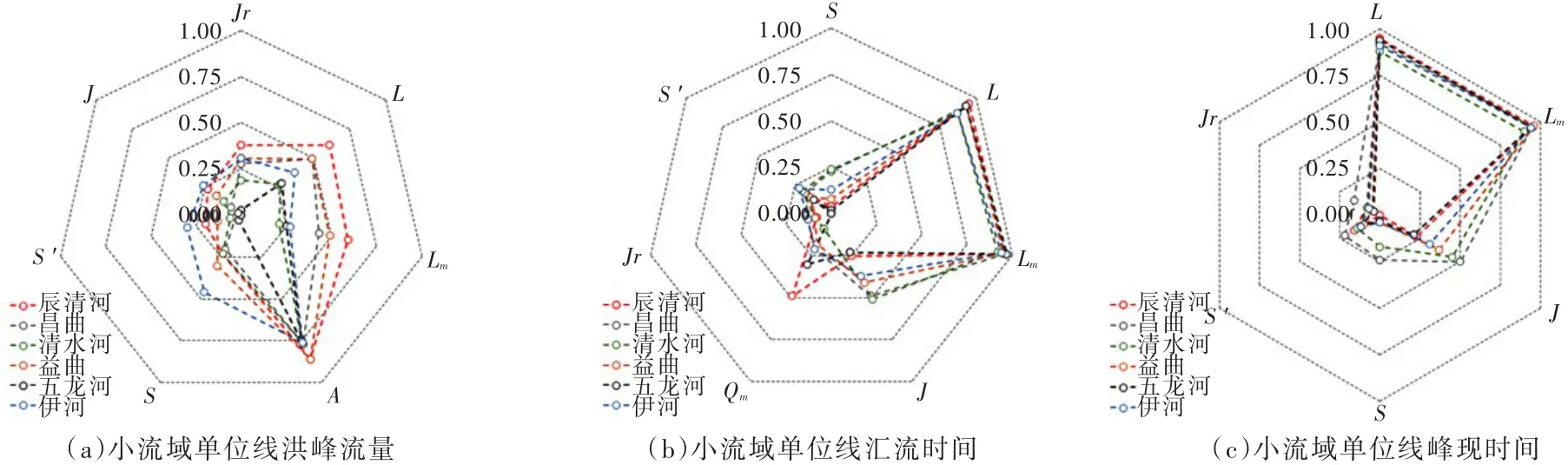
图4 部分典型流域相关系数分布

所选小流域属性主要表征了小流域的面积、比降、汇流路径长度等特性，小流域属性与分布式单位线特征值之间存在显著的相关关系，具有汇流成因概念，但不同典型流域的部分属性与特征值间的相关性不一，反映了流域下垫面的空间异质性对洪水集中度和汇集时间的影响。小流域面积表征了小流域集水区域的大小，面积越大，形成的洪水量级越大，相应的洪峰流量也越大；小流域汇流路径越长，水流由坡面和主河道汇集至小流域出口的时间越长，此外，小流域汇流路径长度与小流域面积间存在显著的正相关关系（r=0.82，p＜0.01），小流域单位面积汇流路径越大，小流域对洪水的调蓄作用越大，洪峰流量的坦化现象越明显；河段比降、平均坡度、最长汇流路径比降等特征参数表征了小流域地形的起伏状态，地形越陡峭，水流流速越快，对水流的汇集作用越强，在同一时段内汇集至小流域出口的水流越多、时间越短。对于小流域内部的水流摩阻因素（如糙率）等，暂不考虑，以经验关系中的综合系数来表征，可在后续研究中进一步细化该因素的影响。

综合已有相关研究成果［20-21］、小流域汇流特性分析和上述相关性分析，提出单位线特征值的拟合公式型，如表2、表3所示。

表2 单位线洪峰流量拟定公式型

表3 单位线汇流时间和峰现时间拟定公式型

4.2 洪峰流量拟合评估不同公式型拟合效果不一样，同一公式型在不同流域拟合效果也有差异。各公式型的评估指标如图5所示。总体而言，所有公式型的拟合效果均较好，均方根误差为0.14～0.86 m3/s，合格率为73%～100%，相关系数为0.85～0.99。12个典型流域的最优公式型为拟定公式型4，即长干河、富尔河、辰清河、岷江、龙河、绵河、五龙河、遂川江、西溪河、布柳河、琴江和新安江，主要分布在横断山脉、云贵高原以及太行山沿线等地貌复杂、地形多变的山区，相应的均方根误差为0.21～0.46 m3/s，合格率为90%～98%，相关系数为0.93～0.98；其余18个典型流域的最优公式型为拟定公式型7，即贡曲、佳芦河、小河、汤河、马滩河、亮江、通道河、秋香江、鸭江、昌曲、俄科河、清水河、尼木玛曲、九龙溪、益曲、比江、官渡河和伊河，相应的均方根误差为0.14～0.75 m3/s，合格率为86%～100%，相关系数为0.93～0.99。单位线洪峰流量与流域面积、最长汇流路径长度、河段比降、流域（加权）平均坡度关系密切。小流域源短流急，将已有公式型中的最长汇流路径比降指标细化为坡面和河段两部分，精细地反映了流域地形起伏状态对洪水集中度的影响，在一定程度上提高了拟合精度。

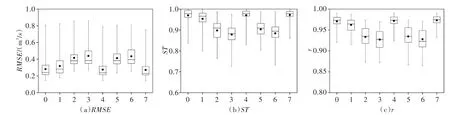
图5 单位线洪峰流量不同公式型评估指标

相比于已有公式型，最优公式型的均方根误差减少了0.01～0.08 m3/s，合格率基本一致，相关系数提高了0～0.03；相比于其他拟定公式型，最优公式型的均方根误差减少了0～0.28 m3/s，合格率提高了0～20%，相关系数提高了0～0.09。图6为部分典型流域最优公式型的单位线洪峰流量拟合散点分布，散点均围绕在1∶1线周围，且大部分小流域散点落在合格范围内，各流域单位线洪峰流量与拟合值吻合较好，构建的公式型和所选小流域属性能较好地反映不同地形地貌类型区洪水集中度的差异性。

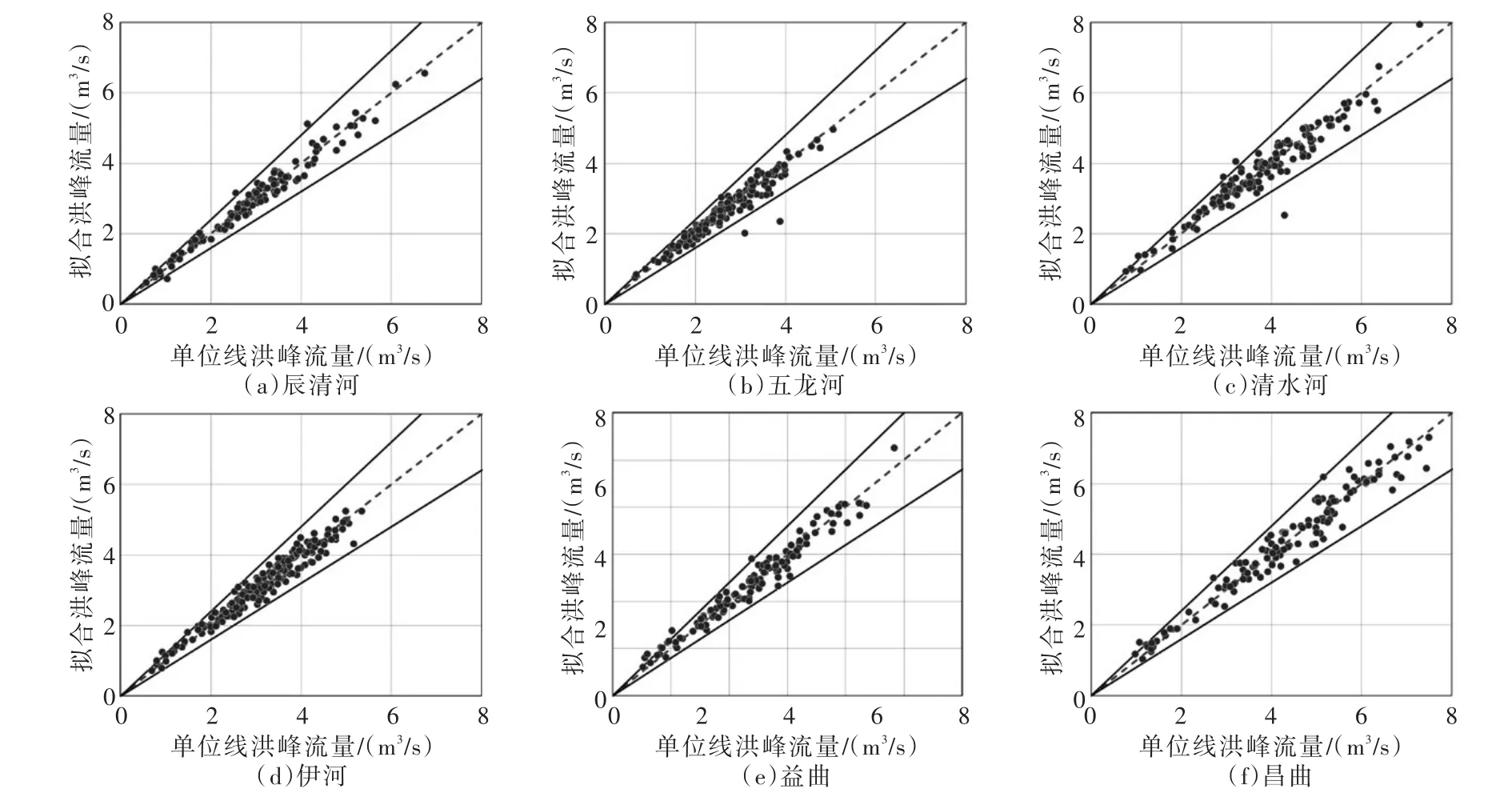
图6 部分典型流域单位线洪峰流量最优公式型拟合散点图

4.3 汇流时间和峰现时间拟合评估单位线汇流时间和峰现时间各公式型的评估指标如图7所示。对于单位线峰现时间而言，所有公式型的均方根误差为3.15～8.46 min，合格率为61%～100%，相关系数为0.82～0.98。所有流域的最优拟合公式型均为拟定公式型3，相应的均方根误差为3.15～7.33 min，合格率为65%～100%，相关系数为0.83～0.98，单位线峰现时间与流域最长汇流路径长度及其比降、平均汇流路径长度关系密切。相比于其他拟定公式型，所有典型流域最优公式型的均方根误差减少了0～1.91 min，合格率变化了-6%～9%，相关系数提高了0～0.03。

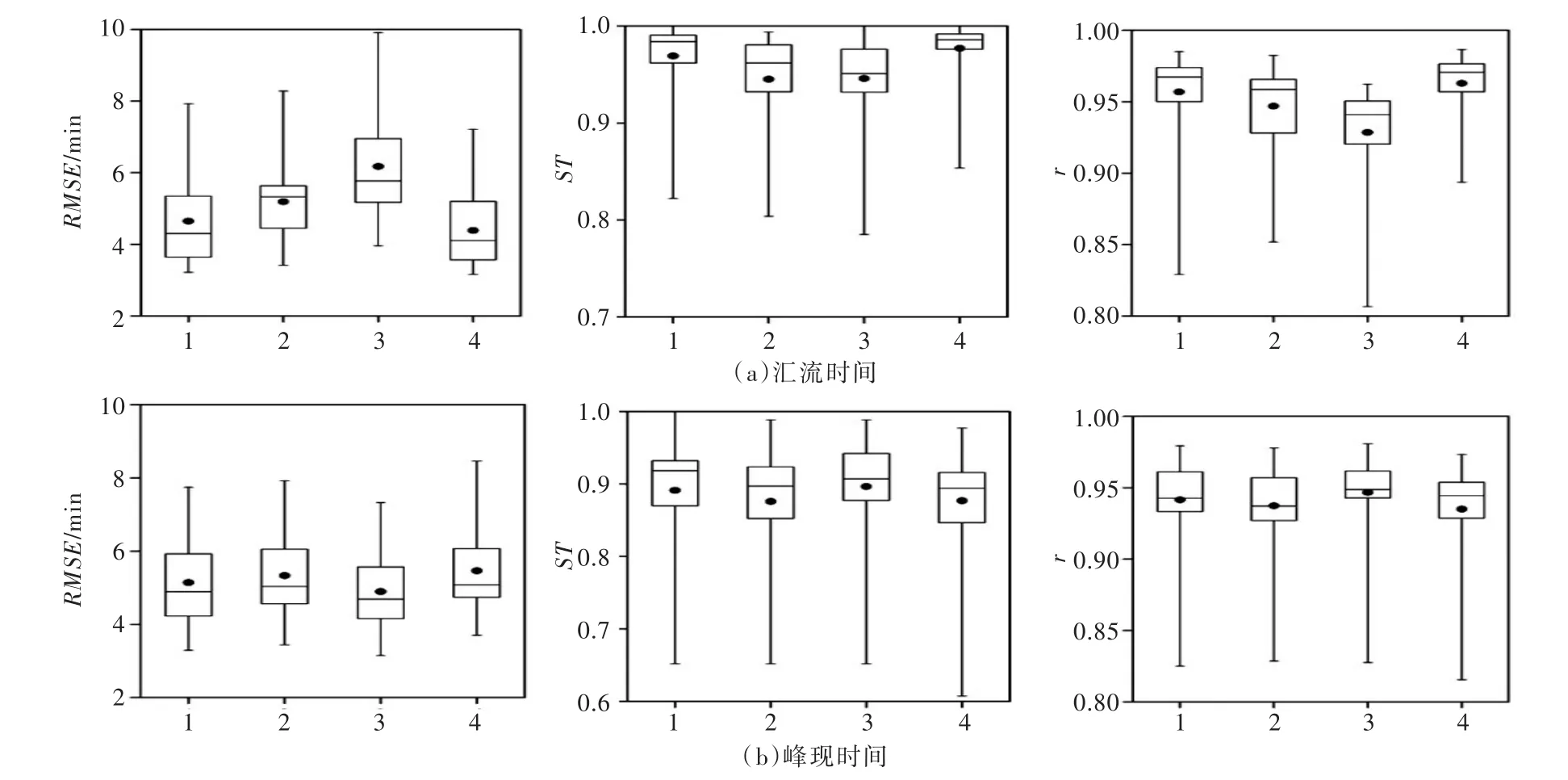
图7 单位线汇流时间和峰现时间不同公式型评估指标

对于单位线汇流时间而言，所有公式型拟合的均方根误差为3.16～9.91 min，合格率为79%～100%，相关系数为0.81～0.99。所有流域的最优拟合公式型为拟定公式型4，相应的均方根误差为3.16～7.21 min，合格率为85%～100%，相关系数为0.89～0.99，单位线汇流时间与流域最长汇流路径长度及其比降、单位线洪峰流量关系密切。相比于其他拟定公式型，所有典型流域最优公式型的均方根误差减少了0.02～3.29 min，合格率提高了0～16%，相关系数提高了0～0.09。图8为部分典型流域最优公式型的单位线汇流时间拟合散点分布，散点均围绕在1∶1线周围，且大部分小流域散点落在合格范围内，各流域单位线汇流时间与拟合值吻合较好，构建的公式型和所选小流域属性能较好地反映不同地形地貌类型区的洪水汇集时间的差异性。总体而言，采用反映小流域汇流非均质分布特性的流域地形地貌属性进行分布式单位线综合分析，具有汇流成因概念，避免了传统综合单位线法普遍存在的主观性，拟合精度高，适于缺资料地区中小流域暴雨洪水计算［22］。

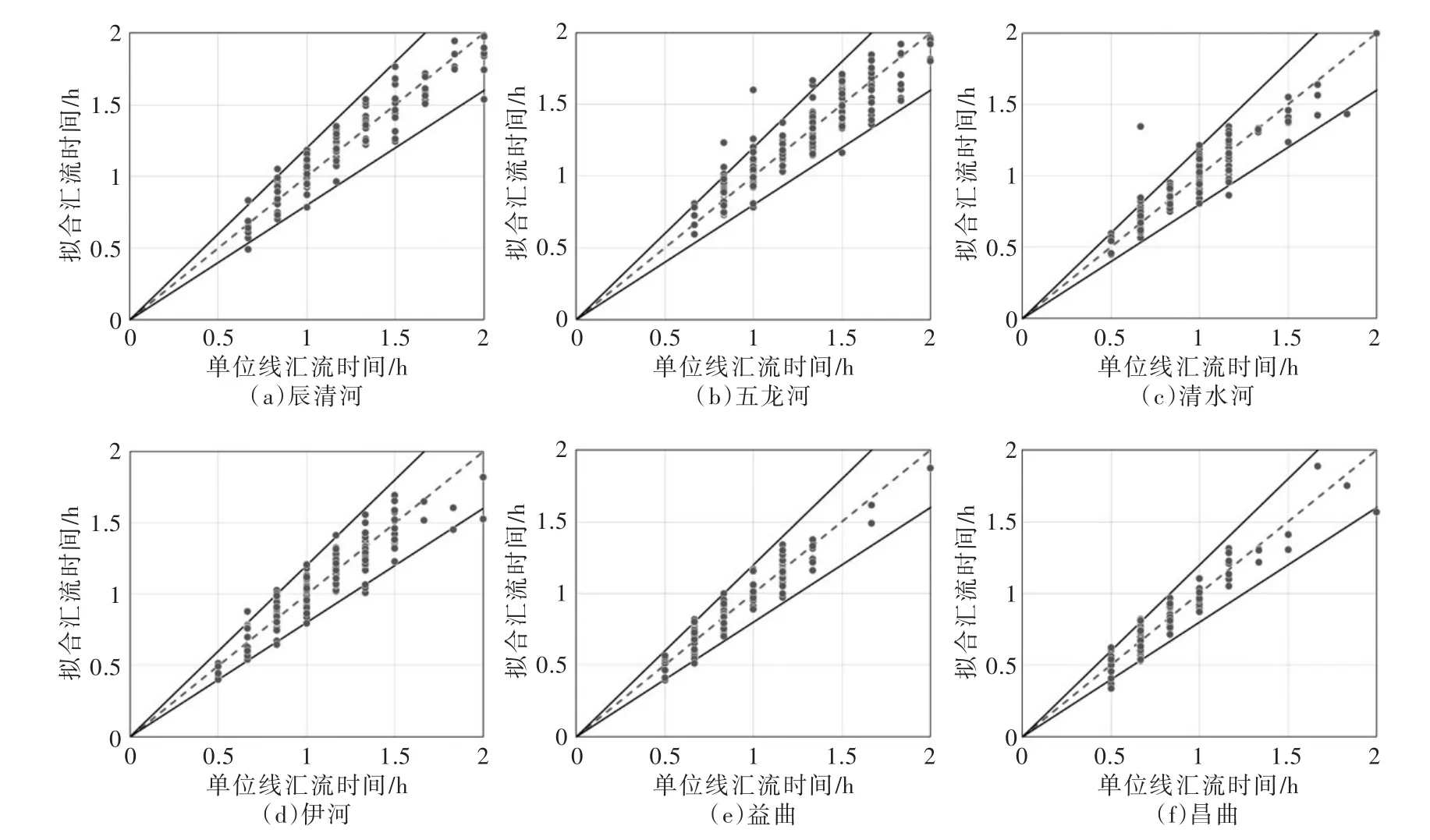
图8 部分典型流域单位线汇流时间最优公式型拟合散点图

5 结论

本文以全国30个不同地形地貌类型区的中小流域为典型流域，基于全国小流域数据集，采用相关性分析和基于最小二乘法的多元回归非线性模型进行小流域分布式单位线的综合分析。主要结论为：（1）小流域不均匀系数、加权平均坡度较好地反映了小流域汇流的非均质性，可用于分布式单位线的综合分析。全国73.6%的小流域流路分布较不均匀，其中9.7%的小流域流路质心偏下游，水流汇集路径较短，较易形成山洪；34.5%的小流域坡面侧剖面呈“凹”型分布，侵蚀强度较大，易于形成山洪滑坡地质灾害，9.2%的小流域侧剖面呈“凸”型分布，坡面有利于排水，但水流冲刷作用也较强，容易造成水土流失。（2）30个典型流域小流域单位线洪峰流量与小流域面积、平均/最长汇流路径长度存在中度～强度正相关关系，与单位面积汇流路径长度存在负相关关系；单位线汇流时间、峰现时间与小流域平均/最长汇流路径长度存在较强的正相关关系，与最长汇流路径比降存在中度负相关关系，单位线汇流时间与洪峰流量存在中度正相关关系；其余属性与单位线特征值间的相关程度不一。（3）12个典型流域小流域单位线洪峰流量拟合的最优公式型为即长干河、富尔河、辰清河、岷江、龙河、绵河、五龙河、遂川江、西溪河、布柳河、琴江和新安江，其余18个典型流域的最优公式型为即贡曲、佳芦河、小河、汤河、马滩河、亮江、通道河、秋香江、鸭江、昌曲、俄科河、清水河、尼木玛曲、九龙溪、益曲、比江、官渡河和伊河；汇流时间和峰现时间的最优公式型分别为和洪峰流量和汇流时间的合格率均在85%以上，相关系数在0.90以上，峰现时间的合格率和相关系数分别大于65%和0.80。（4）本文主要分析了降雨量为30 mm、时段长为10 min的分布式单位线，今后应进一步开展不同雨强、时段长的分布式单位线的综合分析，继续开展小流域内部水流摩阻因素对小流域汇流特性的影响量化研究，以进一步提高单位线综合分析的精度。