科学运用“思维导图”了解数学解题套路

■余泓杰

思维导图是一种有效的学习方式。通过思维导图对知识系统化梳理,我们会了解关键信息,掌握解题套路,完善认识,进而提高自己的解题能力。思维导图的绘制过程中,我们可以从多角度、多方位去总结解题套路,梳理知识系统,通过逻辑思考和推理判断的方式形成自己对知识的系统性理解,掌握解题方法,这样面对任何问题都会胸有成竹。

一、运用思维导图总结易错难题，明确解题套路

数学试题对同学们的各种能力要求比较高,稍不注意就会出现错误。我们的错误原因是多样的,包括了逻辑推理错误、空间想象错误、计算错误、综合分析错误等。

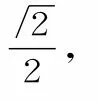
易错分析：没有注意到平方式非恒等变形的过程,容易产生增根。

二、运用思维导图总结解题思路，明确解题套路

数学试题的解答都是有一定规律可循的,只要我们掌握了这些解题思路和解题规律就会在答题过程中顺利操作,快速形成自己的思路,解决问题。我们要经常性地对解题思路和方法进行总结,在大脑中对解题的一般规律有一个清楚认识,构建出自己的解题思维导图。例如试题中经常出现的函数的单调性、极值、最值问题,在思维导图中我们可以对经常考查的试题解题思路总结规律,总结通性通法,形成完整性认识。这样就可以通过具体试题来形成规律性认识。

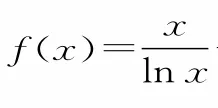
(1)若f(x)在(1,+∞)上单调递减,求实数a的取值范围。

(2)若a=2,求函数f(x)的极小值。

(3)若方程(2x-m)lnx+x=0在(1,e]上有两个不等实根,求实数m的取值范围。

分析：通过对试题的分析和探究会发现,第一问涉及函数单调性问题,第二问求的是函数的极小值问题,而最后一问则是根据实根来求取值范围的问题。面对这样的试题解答时应该注意:

第一步:先确定函数的定义域,再对f(x)求导。

第二步:求方程f′(x)=0的实数根。

第三步:利用f′(x)=0的根和区间端点的x的值,从小到大顺次将定义域划分成若干个区间,列出表格。

第四步:由f′(x)的正负,确定f(x)在各区间内的单调性。

三、运用思维导图总结不同题型，明确解题套路

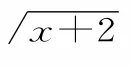
A.[-2,2) B.(-2,2)

C.[-2,0) D.(0,2)

图1

结束语：通过绘制思维导图,我们对不同题型的解题方法和解题思路会有一个清楚的认识,建构解题套路和解题方法,形成系统性认识,进而提高自己答题的准确性和解题能力。