提高汽轮发电机定子烘房能效的研究
汪腊珍, 潘卫国, 王文欢, 秦 岭, 潘衍行
(1. 上海电力学院 能源与机械工程学院, 上海 200090;2. 上海发电环保工程技术研究中心, 上海 200090)
近年来,在电力、钢铁、化工等现代化程度相对发展较快的工业领域,出现了很多以高效节能生产为目标的研究成果[1-2]。在装备制造业中,汽轮发电机定子烘焙是一个高耗能、高排放的环节之一,降低烘焙过程的能耗和成本,提高工件烘焙质量是烘焙技术发展的主题之一。
刘洪伟等[3-4]在汽轮发电机定子线圈、线棒的制造设备、工装工具和工艺方面进行创新与改进。史进渊[5]对大型汽轮发电机定子线圈F级绝缘的老化因子与加速寿命进行了预测。DEPREE N等[6-7]通过熔炉建模来研究连续退火炉中的温度,以优化热处理质量、工厂产量和能耗。靳慧勇等[8-9]通过对多风路空冷汽轮发电机定子内的流体流动与传热进行数值模拟。在定子的烘焙过程中容易出现蒸汽耗量大、热效率低、烘干成本高等一系列问题[10],烘房是定子加热的必备设施,在烘房的设计过程中,通常只关注烘焙的时间长短,而忽视了烘房的热效率。
笔者通过对某电厂汽轮发电机定子烘焙过程进行能效测试,以求得烘房的热效率,并通过实验和数值模拟寻求提高烘房能效的方法。
1 能效测试
该厂定子烘房烘焙包含定子嵌线三次烘焙,分别是在下层线圈入槽后(第一次烘焙)、上层线圈入槽后(第二次烘焙)、鼻端绝缘后(总烘焙),笔者测量的烘焙工艺是第二次烘焙。烘房加热系统由主、辅热风系统组成。烘房内室有效尺寸为14 000 mm×6 400 mm×7 400 mm,设备基本参数见表1。
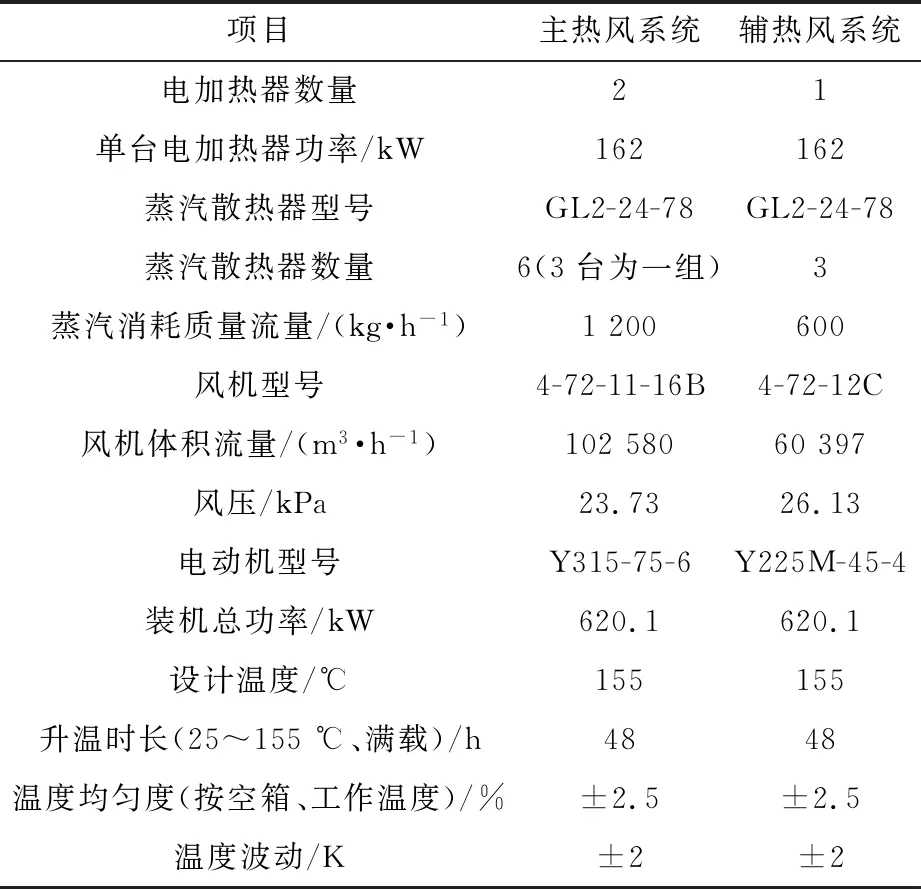
表1 设备的基本情况
2 散热损失分析
2.1 散热损失计算
图1为烘房热风管道示意图。
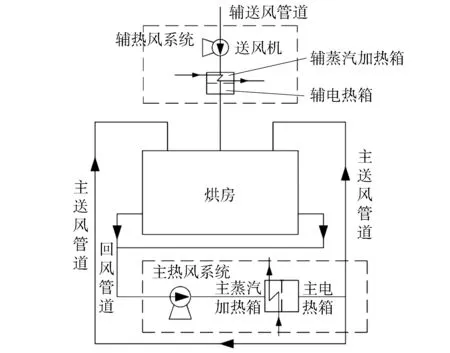
图1 烘房热风管道示意图
表2为红外线热成像仪测量的各区域温度。当烘房温度分别达到80 ℃、130 ℃时,烘房内部会进行保温处理,故在这两个保温阶段进行测量,计算在这两个阶段的散热损失,最后取平均值来计算烘房工作期间的散热损失。

表2 各区域温度测量结果 ℃
假设环境温度为25 ℃,计算得到烘房温度对应的各部分散热损失见表3。
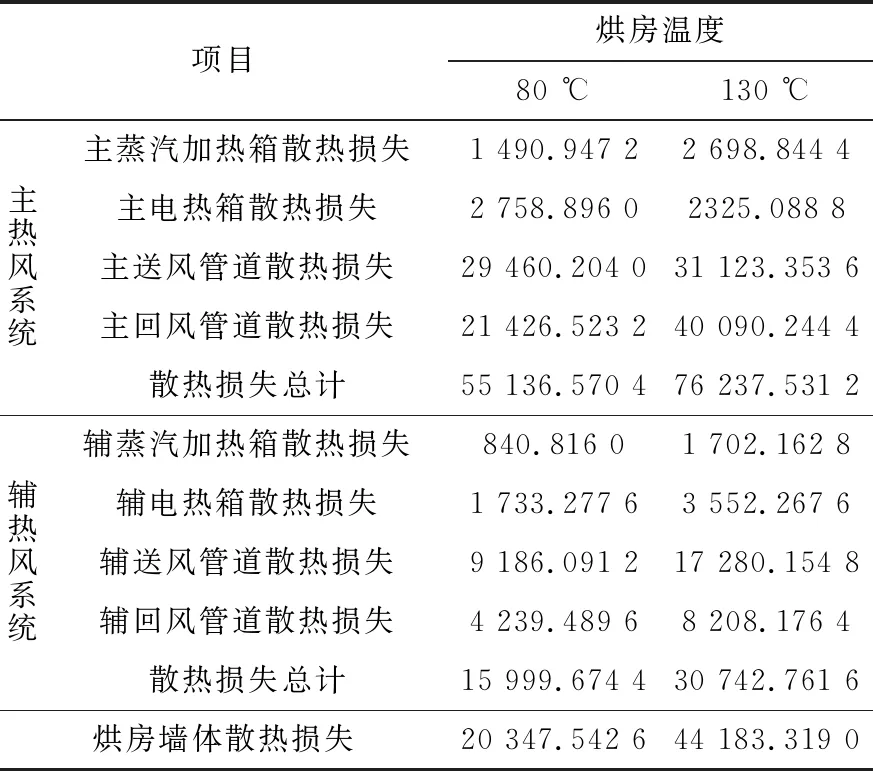
表3 烘房各部分散热损失 kJ/h
2.2 热量输入
该工件第二次烘培时间总计为45.58 h,蒸汽加热箱一直处于额定功率运行,保障工件加热的均匀性。利用三相智能电量仪,记录了烘房在定子加热期间的用电量,测得定子此次烘焙用电量为2.723 76×107kJ。额定功率下,主蒸汽加热箱蒸汽质量流量qm1为1 200 kg/h,蒸汽温度为150 ℃;辅蒸汽加热箱蒸汽质量流量qm2为600 kg/h,蒸汽温度为150 ℃。主蒸汽加热箱的供热量Qzq可根据下式估算:
Qzq=qm1(c1t1-c2t2)
(1)
式中:c1、c2分别为换热前、后主蒸汽的比热容,kJ/(kg·K);t1、t2分别为换热前、后主蒸汽的温度,℃。
辅蒸汽加热箱的供热量Qfq可根据下式计算:
Qfq=qm2(c1t1-c3t3)
(2)
式中:c3为换热后辅蒸汽的比热容,kJ/(kg·K);t3为换热后辅蒸汽的温度,℃。
该烘房整体输入热量Qsr为:
Qsr=Qd+Qzq+Qfq
(3)
式中:Qd为电能产生的热量,kJ/h。
2.3 热量输出
2.3.1 加热定子的有效热
发电机定子材质为硅钢,其质量md为66 000 kg、比热容cg为0.46 kJ/(kg·K),定子被加热有效热可按下式计算:
Qyx=md(tout1-tin1)cg/τ
(4)
式中:tin1为工件进入退火炉的初始温度,℃;tout1为工件保温温度,℃;τ为工件加热至保温温度的时间,h。
2.3.2 砌体蓄热
估算砌体材料为石棉,其体积Vqt为95.05 m3、密度ρqt为80 kg/m3、比热容cqt为0.8 kJ/(kg·K),故砌体蓄热为:
Qxu=Vqtρqtcqt(tout2-tin2)/τqt
(5)
式中:tin2、tout2为加热前、后砌体的温度,℃;τqt为砌体加热至保温温度的时间,h。
2.3.3 热平衡对比结果
烘房输入热量为1 255 934.01 kJ/h,列出该定子加热过程的输出热量表,具体见表4。
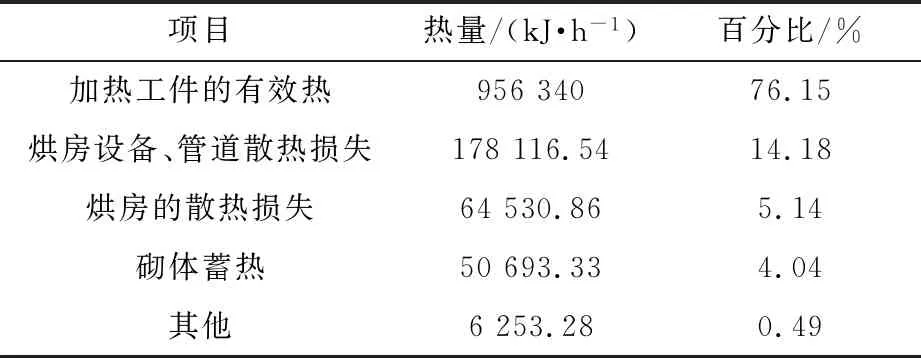
表4 输出热量表
该烘房的热效率为76.15%,烘房的热效率反映了热能的利用情况,是评价烘房的重要指标[11]。热损失主要在于该烘房设备、管道处,假设在烘房温度达到130 ℃,管道外壁的温度控制在38 ℃,求得各管道散热损失见表5。由此计算烘房设备、管道总共散热损失为112 464.6 kJ/h,散热损失率为8.95%,较原始散热损失率(14.18%)降低了5.23百分点。
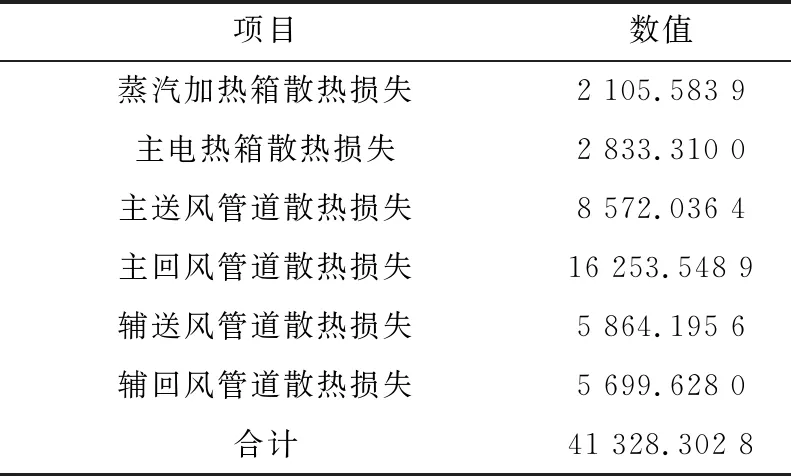
表5 管道外壁温度为38 ℃时的散热损失 kJ/h
3 内部传热的数值模拟
3.1 物理模型
烘房外部结构和尺寸见图2,烘房前墙上有一个圆形辅热风进口,烘房顶部有10个矩形的主热风进口。烘房外墙铺设有用石棉做成的保温层,保温层厚度为500 mm。烘焙定子为600 MW水氢冷定子铁心,长度为6 300 mm,最大水平高度为5 346 mm。

图2 烘房外部结构和尺寸
3.2 数学模型
笔者主要模拟烘房内热空气的流动与传热,将热空气作为可压缩理想气体,空气在烘房内的流动满足连续性方程、动量方程和能量方程[12],空气在烘房内的流动为紊流,湍流模型选用标准k-ε模型[13]。
3.3 网格划分和边界条件
计算区域为整个烘房区域,按照实际烘房尺寸进行建模,利用ANSYS ICEM软件对模型进行网格划分,网格采用六面体结构化网格,后墙辅助热风进口部分采用O形网格技术进行处理[11],网格数量为12万,三维网格划分见图3。

图3 烘房计算区域网格划分示意图
辅助热风进口和主热风进口均采用速度入口边界条件,出口采用压力出口,出口表压为大气压力,模拟计算其他条件见表6。
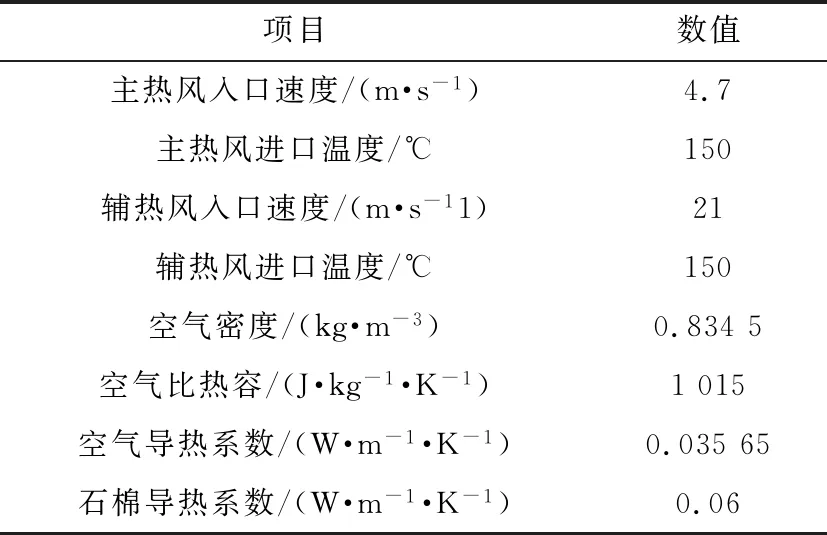
表6 模拟计算其他条件参数
为了评定烘房内部流场及温度场的分布是否合理,以比较不同的调整方案的优劣,按照图4所示的位置选取纵向截面对流场及温度场进行分析。
图4 纵向截面示意图
3.4 模拟结果分析
3.4.1 原始设计方案
对原始设计方案进行模拟的结果见图5。
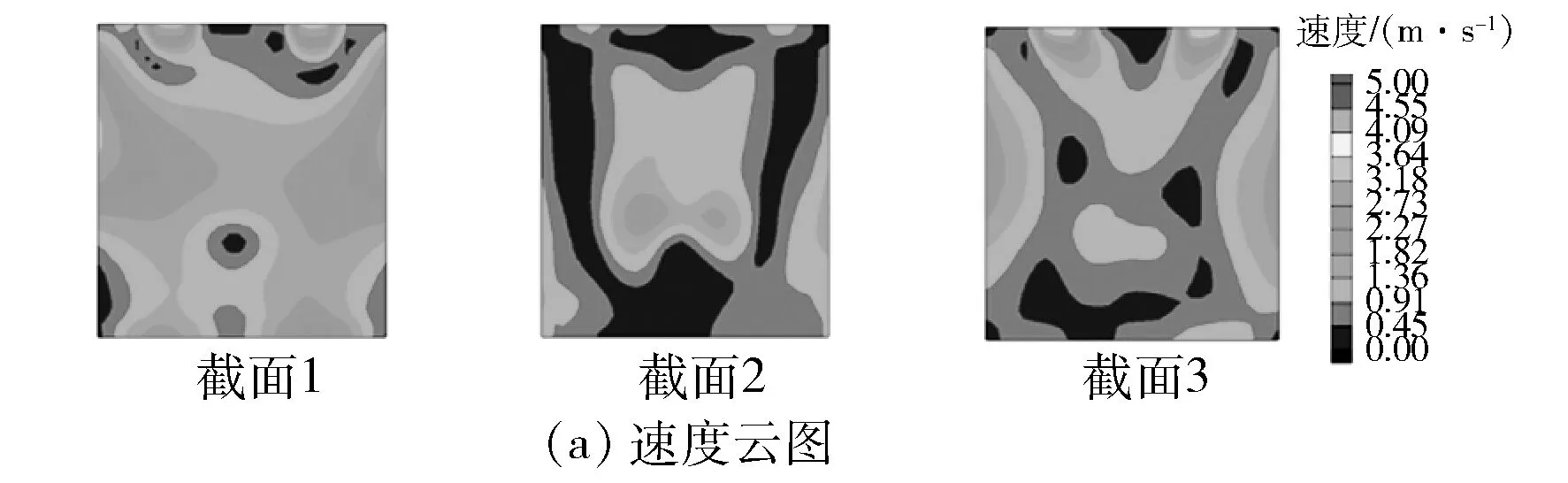
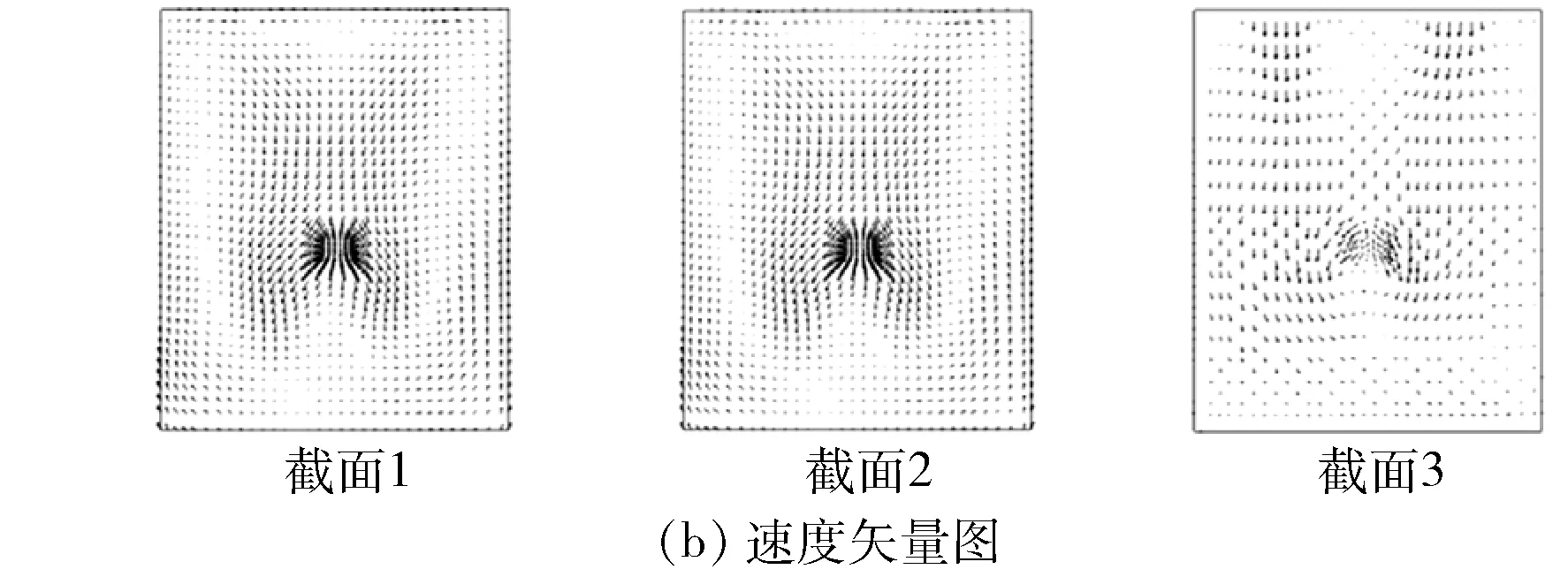
图5 原始设计模拟结果
由图5可得:原始设计方案中,烘房内部热风在靠近烘房前墙部分产生了堆积,导致前墙部分温度比后墙部分温度高,前后温度分布不均;截面3速度集中在四周,中心位置速度较小,并且从速度矢量图中可以看出,靠近辅助热风进口位置截面矢量图分布稀疏,空气在烘房内部扰动较小,导致热风与烘房内部加热工件换热较差;截面3高温区域主要集中在中心偏上位置,而加热的工件往往处在烘房下部,可能导致工件上部区域受热比下部区域受热多,工件受热不均匀。为了得到理想的烘房气流分布和温度分布,对烘房的喷口进行优化调节。
3.4.2 调节方案
(1) 改变喷口射流方向。
将主热风喷口方向调整为斜向下60°喷入烘房,喷入角度见图6。
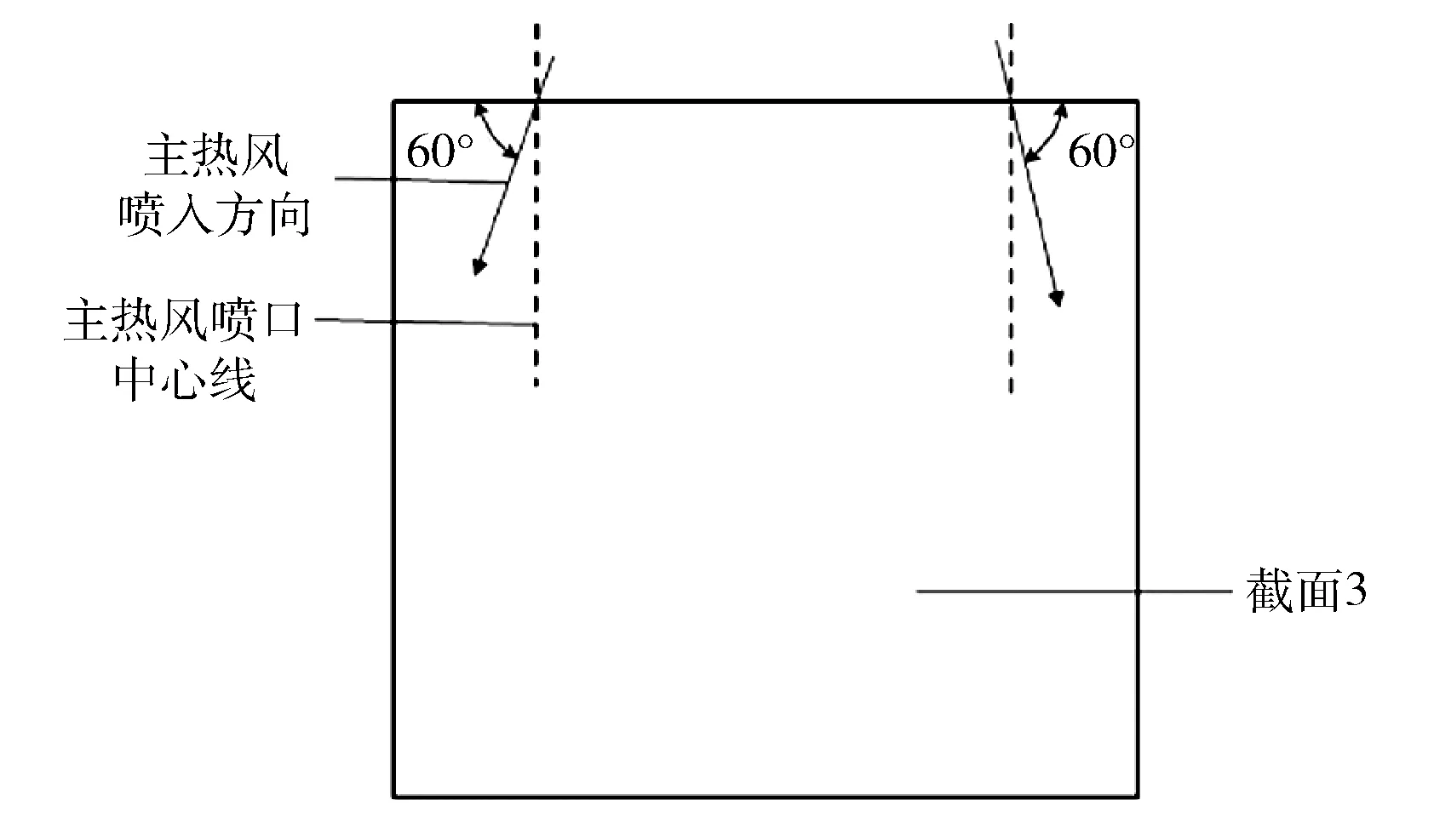
图6 主热风喷入示意图
按照此设计方案对烘房进行了模拟,结果见图7。

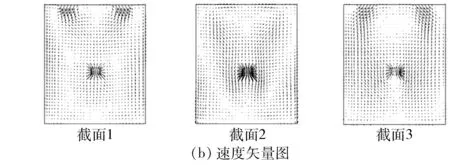
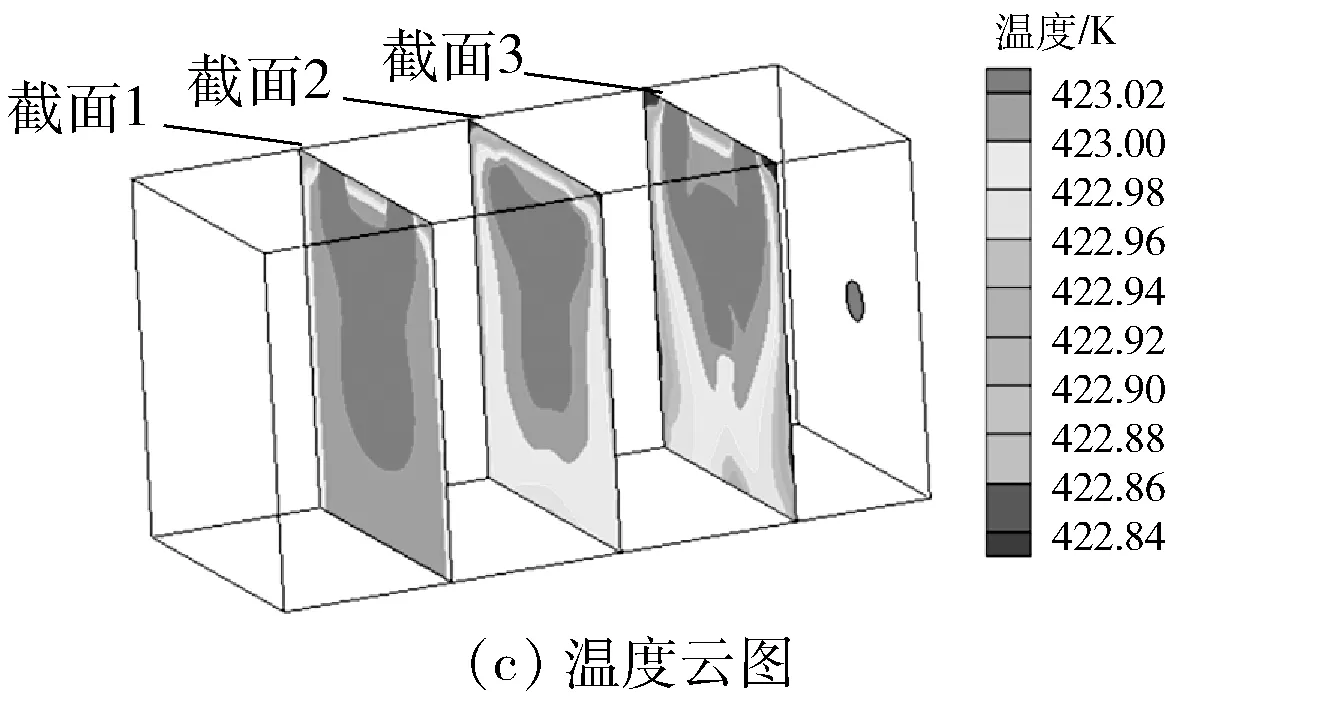
图7 改变喷口射流方向模拟结果
由图7可得:只有辅助热风进口位置的速度分布集中在中心位置,截面1、2的速度分布并不均匀,倾斜的喷口会导致高温更加偏向烘房中心偏上的位置,由于倾斜的喷口导致在烘房中心偏上位置形成两个涡旋,将热气流整体抬升;并且在靠近烘房前墙位置的温度分布均匀度低于原始设计方案。
(2) 改变喷口面积。
图8为保持主热风的风量不变的情况下,喷口面积缩小10%后的模拟结果。
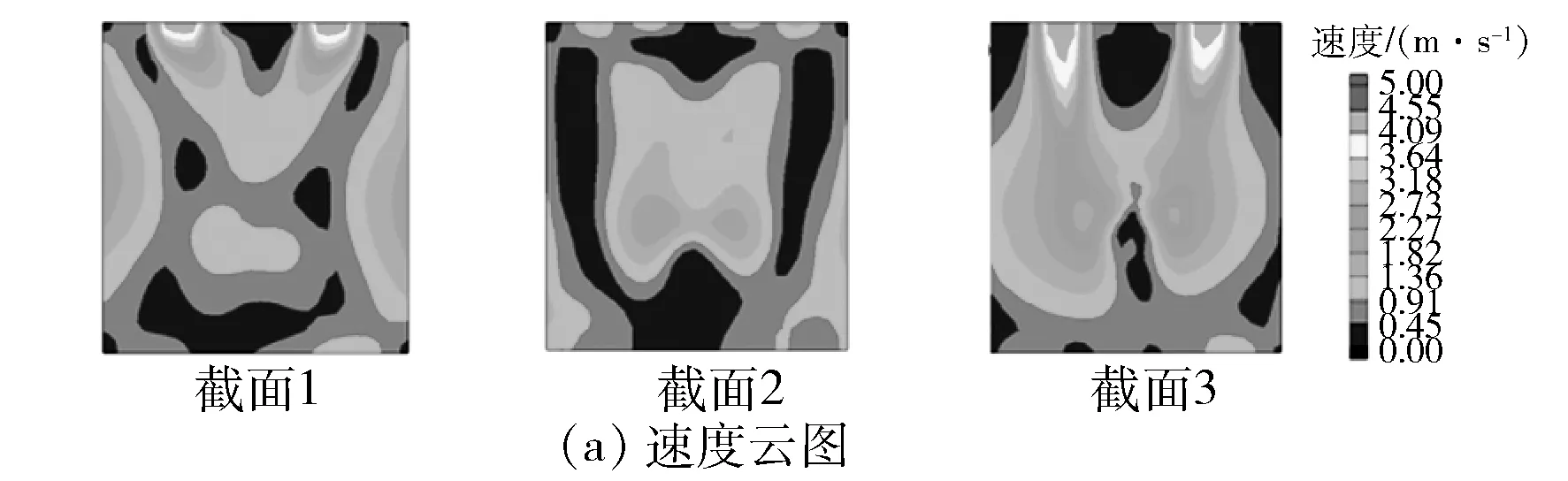
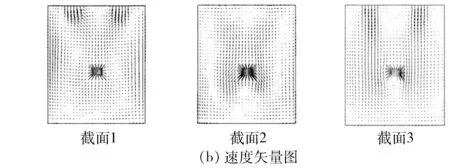
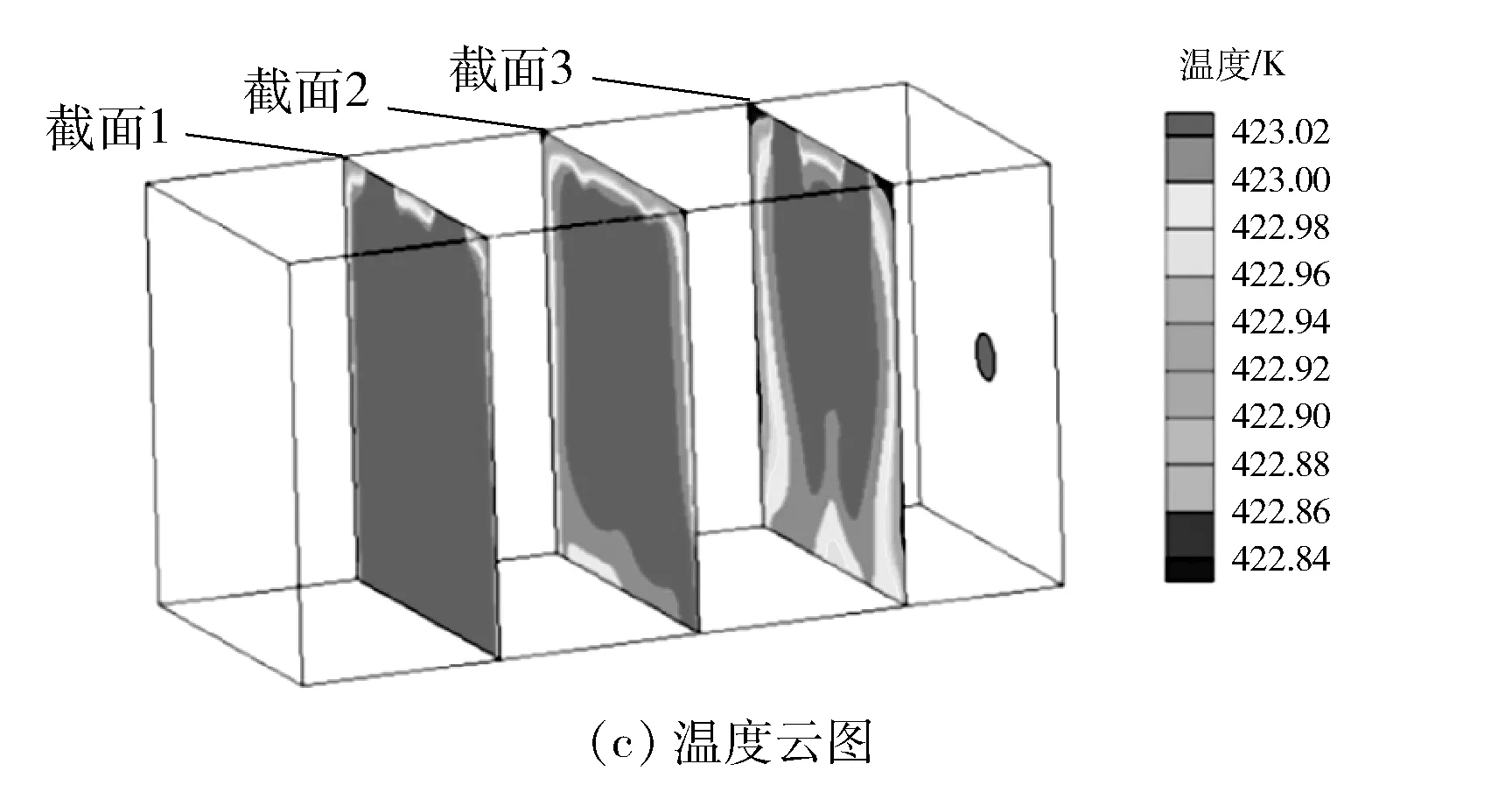
图8 改变喷口大小模拟结果
由图8可得:缩小主热风喷口对改善烘房内部气流和温度有着显著效果,缩小喷口面积后,烘房内部气流分布均匀,温度分布相对合理。在保持热风风量不变的情况下,缩小喷口面积会使喷入烘房的主热风速度显著增加,原始设计方案下的喷口喷入速度过小,导致喷入的热风与辅助热风不易形成强烈的紊流,流场扰动不够强烈;垂直喷入的高速主热风与水平方向喷入的辅热风在扰动作用下形成涡旋,并且气流混合更加均匀。缩小喷口后,前墙温度依然比后墙温度高,主要是烘房出风口位于烘房靠近后墙部分,在烘房靠近前墙部分集聚了较多的热空气,导致烘房靠近前墙的位置温度稍高;但是改变喷口面积后,烘房温度分布更加均匀合理。
3.4.3 换热量分析
分别取截面1、2、3中高度为定子高度的温 度平均值作为气流温度、速度平均值作为气流速度,根据数值模拟结果:原始工况气流温度、改变喷射角度后气流温度、缩小喷口面积后气流温度分别为49.90 ℃、149.84 ℃、149.98 ℃,原始工况气流速度、改变喷射角度后气流速度、缩小喷口面积后气流速度分别为1.71 m/s、1.66 m/s、1.81 m/s。
取环境温度为20 ℃,温度变化本身不大,所以忽略温度变化对物性参数的影响,计算得到改变气流喷射角度后换热量相对于原始工况换热量减少了2.41%,缩小喷口面积后换热量相对于原始工况换热量增加了4.75%,说明改变气流喷射角度对于增加换热量并没有贡献,反而会减小换热量;缩小喷口面积,增大喷射速度,可使换热量增加。
4 结语
笔者通过实验和数值模拟以提高烘房能效,即降低烘房外在的散热损失和强化烘房内部流场的均匀性,并得出如下结论:
(1) 通过对发电机定子烘房的能效测试发现,整个烘房的散热损失占比最大的是烘房设备、管道的散热损失,占14.18%,假如在其他条件不变的情况下,烘房管道外壁温度降到38 ℃,该区域的散热损失率将降低5.23百分点。
(2) 原始设计方案中,在烘房的前墙部分热风产生了堆积,前后温度分布不均匀,并且烘房气流扰动不强,与工件换热不强烈。
(3) 将主热风喷口方向调整为斜向下60°喷入烘房,使高温区域提高到了烘房中心线以上,不利于与工件的换热;将主热风喷口缩小10%,烘房内产生涡流,气流扰动明显,烘房温度分布较为均匀,气流与工件的换热量提高4.75%。

