数据协调在燃气-蒸汽联合循环机组汽轮机排汽焓计算中的应用
张浩峰, 胥建群, 黄喜军, 陈晓欣, 皇甫泽玉
(东南大学 能源热转换及其过程测控教育部重点实验室, 南京 210096)
燃气-蒸汽联合循环机组性能的计算与设备的故障诊断离不开准确的测量数据;然而,在工程实际中,精准的测量数据不易获得[1-2]。例如,测量仪表随着使用年限的增加精度越来越低,传感器由于长期工作在高温和高压的环境下易发生故障,受到电磁干扰后传感器测量结果严重偏离真实值等情况,不能真实反映机组运行状态。因此,如何提高测量数据的准确性,确保燃气-蒸汽联合循环机组高效、经济和安全运行是当前重点研究方向之一。
燃气-蒸汽联合循环机组性能监测包括数据提取、性能计算、故障检测、故障定位和故障预测等方面。在这些领域中,国内外学者通过理论分析、热力试验和仿真模拟等方法做了大量的研究[3-5]。MOHAMMADI R等[6]提出了一种基于动态神经网络的燃气轮机故障检测方法,在识别非线性系统上具有很大优势,在仿真研究和试验中都能够有效地对机组故障进行检测。HENTSCHEL J等[7]基于APROS仿真平台搭建燃气-蒸汽联合循环模型,研究不同负荷下主要性能参数对机组经济性的影响。ONODA T等[8]提出了一种基于支持向量机(SVM)的燃气轮机轴承故障诊断方法。通过提取振动信号的特征向量作为模型的输入量,然后利用SVM智能分类确定汽轮机轴承运行状态和故障类型,结果表明模型提出的小样本SVM分类方法能够准确、有效地对燃气轮机轴承的工作状态和故障类型进行分类。
除此之外还有常见的方法,如模糊逻辑、遗传算法、神经网络、数据协调等。数据协调技术是利用工业生产过程原理机制和测量数据的冗余信息,结合统计分析原理和学习算法等手段,降低测量数据在测量、处理和传输过程中的随机误差,使协调后的数据能够满足系统能量与质量守恒的平衡关系,以便指导生产运行[9-10]。
汽轮机低压缸效率变化对机组出力和热耗影响显著,是汽轮机运行中重要的性能指标。因为无法获取准确的低压缸效率,通常电厂性能考核时,低压缸效率并不作考核标准。但是在机组现场运行期间,受负荷、运行方式或环境温度等因素的影响,运行状态会发生变化,偏离最佳运行状态。因此,现场运行需要获取准确的低压缸效率并对其进行监测,使机组维持在高效率下运行,保证机组运行经济性。计算低压缸效率的难点是得到精准的排汽焓,凝汽式汽轮机和核电汽轮机低压缸排汽通常处于湿蒸汽区,无法直接通过测量其压力与温度确定其焓,要通过计算获取。排汽焓可根据质量平衡、能量平衡等方程,对回热机组的热力系统进行计算得到,也可以根据凝汽器能量平衡方程求取,但是在排汽焓的计算过程中,因为测量数据存在误差且数据较多时,测量误差会产生传播和积累,从而影响计算结果。
对于上述排汽焓计算中存在的问题,可采用数据协调进行处理。数据协调技术通过减少随机误差的影响,提高了测量数据的准确性,经过协调以后的数据能够满足系统的质量、能量或者是设备特性方程,更加接近“真值”,得到了优化。根据数据协调的结果,可分析选取适合对象机组的计算方法,对排汽焓进行计算,从而减少误差的累积,提高计算精度。
笔者以某电厂一台燃气-蒸汽联合循环机组汽轮机侧为研究对象,在仿真模型数据基础上,添加不同的误差模拟电厂现场测量数据,对测量数据进行粗大误差识别与数据协调计算,提高测量数据计算可靠性;此外,笔者还针对机组的特点提出了基于功率和基于凝汽器循环冷却水质量流量计算排汽焓的方法,探讨不同的约束方程精度对排汽焓计算的影响。
1 数据协调原理
测量数据的问题具体表现为不平衡性和不完整性。测量数据的不平衡性是指误差的存在使得测量数据不能精确地满足热工过程中一些热力学规律,如测量的每一个数据都满足仪表误差要求,但是数据集却不满足能量、质量平衡或设备的约束平衡。测量数据不完整性是指无法直接获得系统里每一处的测量数据,测量仪器昂贵、安装空间受限和测量条件苛刻等因素都可能是造成该问题的原因。不平衡性和不完整性导致状态监测、设备故障检测和环保监测等系统无法正常工作。通过各种理论和技术提高测量数据的有效性和完善测量数据是非常有必要的,因此数据协调技术被提出。
数据协调的作用是将测量数据进行修正,在调整量最小的前提下,使得测量数据满足系统的约束方程。假设热力系统处于稳态运行,测量数据含有随机误差时可以表示为:
X=X0+ε
(1)
式中:X0为n×1维测量变量的真实值;X为n×1维测量变量的测量值;ε为n×1维测量随机误差,服从均值为0、均方差为σ的正态分布。
根据数据协调的定义,系统处于稳定状态且在满足系统能量和质量等平衡约束关系的情况下,找出合理的测量数据协调值,使其与测量值之差的平方和最小,数学分析上该类的优化问题可以转化为求解满足多个等式约束方程的最小二乘解,即
(2)
(3)
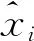
对于式(3)与式(4)来说,若X对U是线性的,则称为线性问题,并存在解析解。线性问题的形式可表示为:
(4)
(5)
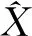
当A、B满秩时,式(6)可通过构造拉格朗日乘子法进行求解,令:
(6)
式中:λ为拉格朗日乘子。

(7)
该方程组的解析解为:
U=(BT(AWAT)-1B)-1BT(AWAT)-1(-AX-C)
(8)
WAT(AWAT)-1(BU+C)
(9)
式中:I为单位矩阵。
当A、B不满秩时,AWAT和BT(AWAT)-1B的逆矩阵不存在而无法求解。针对该问题,可用投影矩阵法解决。构造矩阵B的投影矩阵P0,满足:
P0B=0
(10)
将P0左乘式(5)的线性约束方程,并令A1=P0A、C1=P0C,则有:
(11)
通过构造P0简化了约束问题,整理后的方程逆矩阵也求出。再次运用拉格朗日乘子法求解,可得对应的解析解:
(12)
(13)
2 测量仪表标准偏差
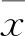
(14)
(15)
σ可从总体的样本中通过估计而来,也可直接通过测量仪表特性计算得到:
(16)
式中:ξmax是测量仪表允许最大误差;zα/2为正态分布的上α分位,可查表或计算得到。
电厂中要检测测量数据的可靠性时,若给定α=0.05,即置信水平为95%,查表可知zα/2=1.96,当有:
(17)
表明此测量值的置信概率<5%,数据存在异常,认为此数据是粗大误差或者设备故障,须要对测量仪表或者设备进行检查。
若有:
(18)
则认为数据落在置信区间内,落在该区间的概率为95%,认为此数据可信。
3 模型建立
为探究数据协调的可行性,笔者对该电厂一台9E燃气-蒸汽联合循环机组汽轮机侧进行验证计算。机组原则性热力系统示意图见图1。

A、C、D2—前轴封漏汽点;B、D1—高压主汽阀阀杆漏汽点;M、D3—后汽封密封汽点;D—D1、D2、D3和D4汇合点;HPS—高压加热器;HPEV—高压蒸发器:HPEC—高压省煤器;LPS—低压加热器:LPEV—低压蒸发器;CP—预热器;CF—轴封加热器
用仿真平台软件EBSILON对其进行建模,为下一步的数据协调计算提供仿真运行数据。
将设计值或仿真平台计算出的数据当作测量值真值,在此基础上加上不同标准偏差的随机误差,构成测量值,模拟电厂数据监测过程。由于该燃气轮机为双压无再热机组,主要汽水流程比较简单,仅有高压主蒸汽和低压主蒸汽两条汽水流程支路,为了增加系统的复杂程度,使得数据协调过程更符合电厂实际情况,现将所有的轴封全部加入到系统数据协调中,并认为大部分轴封的流量均为已知状态。所有已知变量列于表1中,除了轴封外,多数测量变量可从测量仪表或者在联合循环机组分布式控制系统(DCS)可采集到。由于轴封是根据设计资料得到的,故将其相对标准偏差设置得较大,取10%左右;大流量测量精度要求较低,如凝汽器循环冷却水质量流量一般是根据凝汽器中循环冷却水管道进出口压差计算,故其相对标准偏差也可设置成较大的值,在燃气-蒸汽联合循环中,燃料量是系统性能分析的关键测量,精度一般很高,此研究中认为其误差标准偏差为0。

表1 测量变量以及对应的标准偏差

表1(续)
4 校验结果分析
在测量变量的基础上,通过MATLAB软件添加不同标准偏差的正态分布随机误差,对2 000组仿真组数进行独立重复计算。用相对均方根RRMSE来衡量仿真随机数据和协调数据的总体精度情况,其表达式为:
(19)
(20)
相对均方根误差越小,则表明数据与均值的离散程度越小,整体精度越高。图2为2 000组仿真数据与协调值的相对均方根对比,经过数据协调计算后,各路流量相对均方根误差均有不同程度的下降,其中轴封加热器和凝结水质量流量的相对均方根误差下降最明显,分别下降了67.73%和66.65%;高压主蒸汽质量流量和低压主蒸汽质量流量也分别下降了38.01%和0.98%。数据协调算法能够提高测量数据整体的精度。
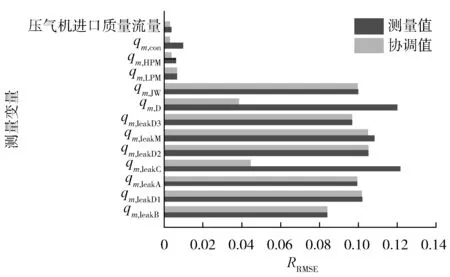
图2 测量数据与协调值的相对均方根对比情况
从冗余数据的特性可知,当系统存在冗余时,冗余数据一般不满足系统约束方程,即方程的残差不为0。数据协调算法的作用就是利用冗余信息,即根据方程残差的大小调整测量变量,降低测量数据的标准误差,使调整后的测量变量满足约束方程,残差变小,进而求出未测变量,最终达到提高检测数据的整体精度的目的。在冗余条件下,图3为数据协调前后凝结水质量流量概率密度对比,数据协调前,凝结水质量流量的期望值为225.757 t/h,误差的标准偏差为2.460 t/h,2 000组数据从218.17 t/h变化到234.50 t/h,呈正态分布变化;数据协调后,凝结水质量流量期望值也呈正态分布变化,其期望值基本不变,但误差的标准偏差降低为0.775 t/h,变化区间由原来的16.32 t/h缩小到5.46 t/h,概率密度分布图变得更加“瘦高”,即经过协调后的凝结水质量流量在期望值附近概率密度陡增,若按协调后凝结水质量流量的“3σ原则”取值,则协调后数据取到223.46~228.11 t/h的概率为99.74%,同一区间下,协调前的凝结水质量流量取到的概率仅为65.56%。

图3 凝水流量测量值与协调值的概率密度对比
数据协调后其他冗余数据的结果对比见表2。经过协调后这些数据的误差标准偏差都有了不同程度的降低。若测量数据基准值没有冗余,那么测量数据只能够算出未测变量,并不能起到提高数据精度的作用;在无冗余的情况下,若测量数据带有误差,则会导致误差在计算中传播和累积,总体数据不仅精度不会提高,严重时有可能还会使数据受到严重影响,精度严重下降。

表2 数据协调前后冗余数据的结果对比
图4、图5分别是数据协调前后功率的相对误差对比。在数据协调前,2 000组数据的汽轮机功率相对误差在±1.5%;经过数据协调之后,汽轮机功率相对误差控制在±0.6%。

图4 数据协调前汽轮机功率相对误差
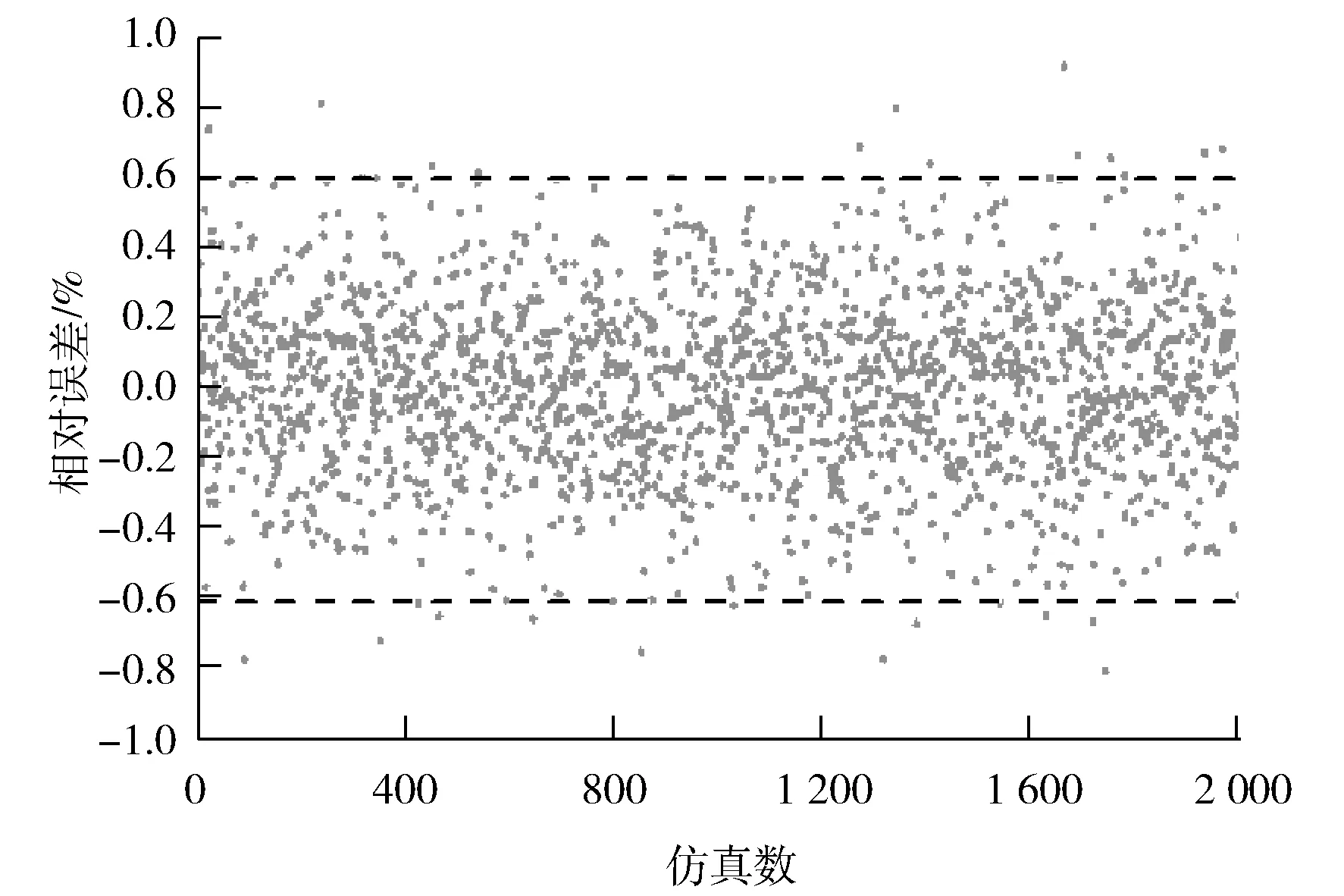
图5 数据协调后汽轮机功率相对误差
5 仪表精度对排汽焓的影响
5.1 计算方法
该双轴燃气-蒸汽联合循环机组没有回热抽汽系统,且机组安装了主蒸汽流量测点。针对这些特点,提出了两种联合循环机组汽轮机侧排汽焓的计算方法,分别是功率法和凝汽器循环冷却水质量流量法。
功率法的约束公式为:
P-qm,HPM(hHPM-hex)-qm,LPM(hLPM-hex)=0
(21)
式中:P为汽轮机功率;hHPM为高压主蒸汽焓;qm,ex、hex分别为排汽质量流量、排汽焓;hLPM为低压主蒸汽焓。
凝汽器循环冷却水质量流量法的约束公式为:
qm,exhex+qm,drainhdrainhdrain-qm,comhcon+
qm,coolingccooling(tcooling,in-tcooling,out)=0
(22)
式中:hdrain为轴封加热器疏水焓;hcon为凝结水焓;ccooling为循环冷却水比热容。
5.2 结果分析
由于汽轮机的排汽焓很大,通常在2 350 kJ/kg左右,即使相对变化仅有±1%,其绝对变化也达到了47 kJ/kg。对于笔者所研究的机组而言,在流量没有误差的情况下,如此大的焓值变化将使汽轮机功率产生4.5%的误差。用两种方法计算得到排汽焓对比见图6。
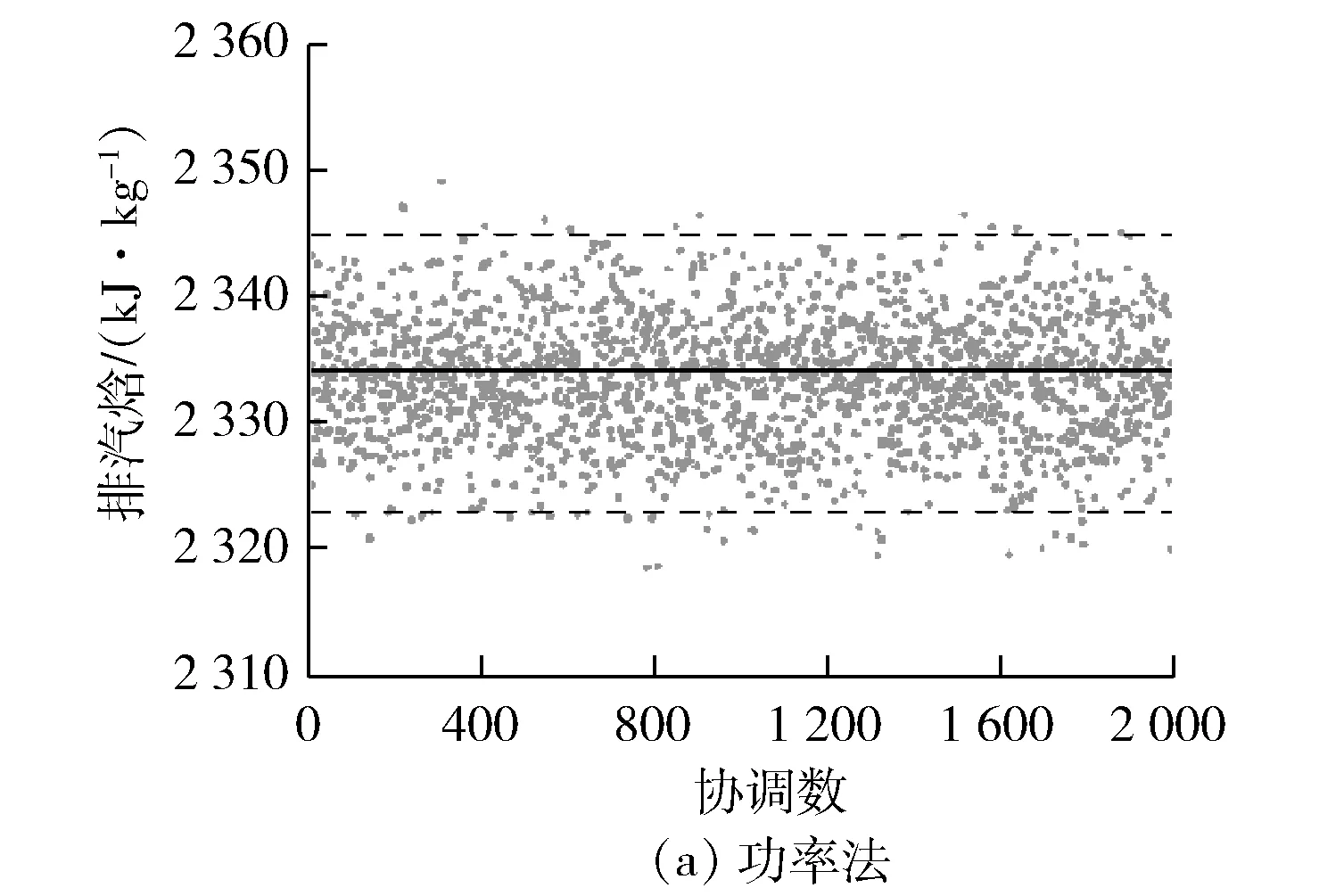
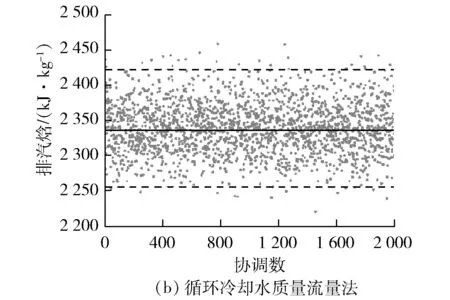
图6 两种方法计算得到的排汽焓对比
由图6可知:用功率法计算出的排汽焓误差带比较窄,相对误差在±0.46%;而用循环冷却水质量流量法计算出的排汽焓相对误差达到了±3.42%。故焓值的精确计算对机组性能计算来说至关重要,在电厂性能计算中排汽焓必须用精度较高的已知测量值进行计算。
现有测量技术和条件难以保证循环冷却水质量流量的测量精度,主要原因是:(1)测点较少且干扰较多,循环冷却水管道直径过大,对于直管道的流量测量,涡流对循环冷却水流动造成一定的影响,该类测量问题工程上要求直管段的长度须达到管直径的10倍以上,许多电厂并不具备这样的条件,实际工程中,电厂一般根据电泵特性对循环冷却水质量流量进行粗略反算;(2)循环冷却水温升较小,管道中压力变化也比较小,对应的压力和温度测量数据会有较大误差,基于凝汽器建立的能量平衡与质量方程的残差就会增大,可信度下降。故相比于功率法,以凝汽器循环冷却水质量流量法计算出的排汽焓精度会有所下降,和排汽焓相关的指标精度均会有大幅度波动。
在用两种方法计算得到排汽焓后分别用排汽焓计算出汽轮机热耗率,得到热耗率相对误差见图7。由图7可知:采用功率法得到的热耗率精度较高,热耗率相对误差控制在±2%,达到工程的要求精度;而采用凝汽器循环冷却水质量流量法得到的热耗率相对误差为±8%。主要是两者使用仪表的精度等级差别较大,发电机功率测量仪表精度为0.02级,精度很高,循环冷却水测量仪表精度相对要低很多。
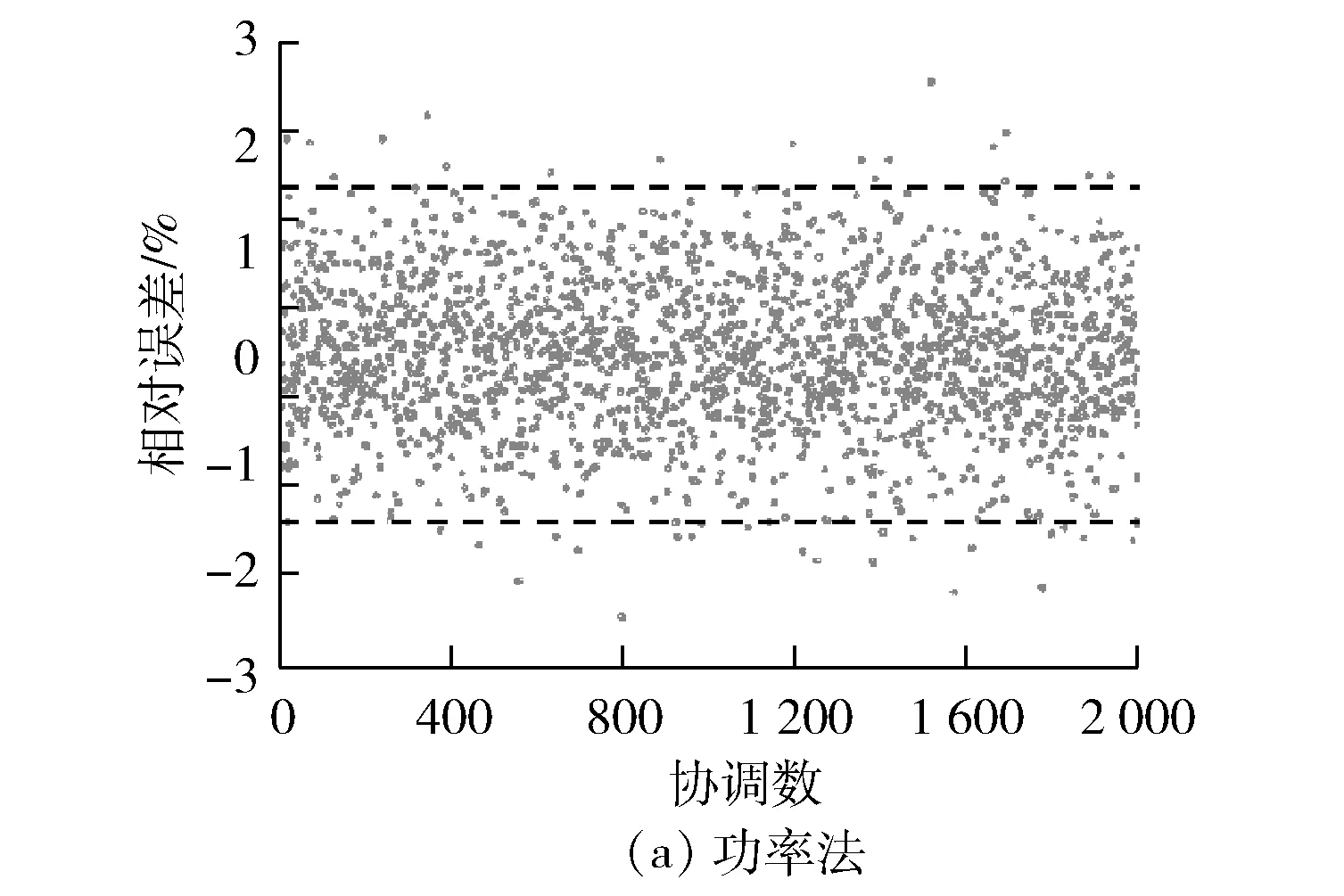
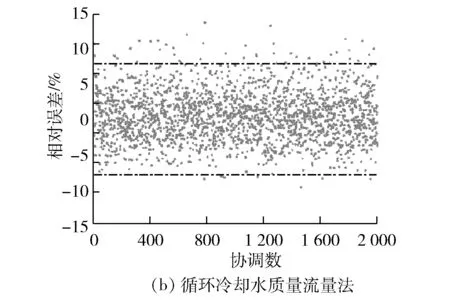
图7 两种方法计算出的热耗率相对误差对比
为探究两种方法在机组变工况中的应用效果,将基于EBSILON软件对机组进行变工况计算,共取7个工况,随后针对每个工况,分别在仿真数据加入2 000组随机误差构成测量数据,进行数据协调计算,考察汽轮机排汽焓的变化。图8为两种方法计算出的排汽焓与其对应的标准偏差随负荷的变化,图9为排汽焓期望值对比。
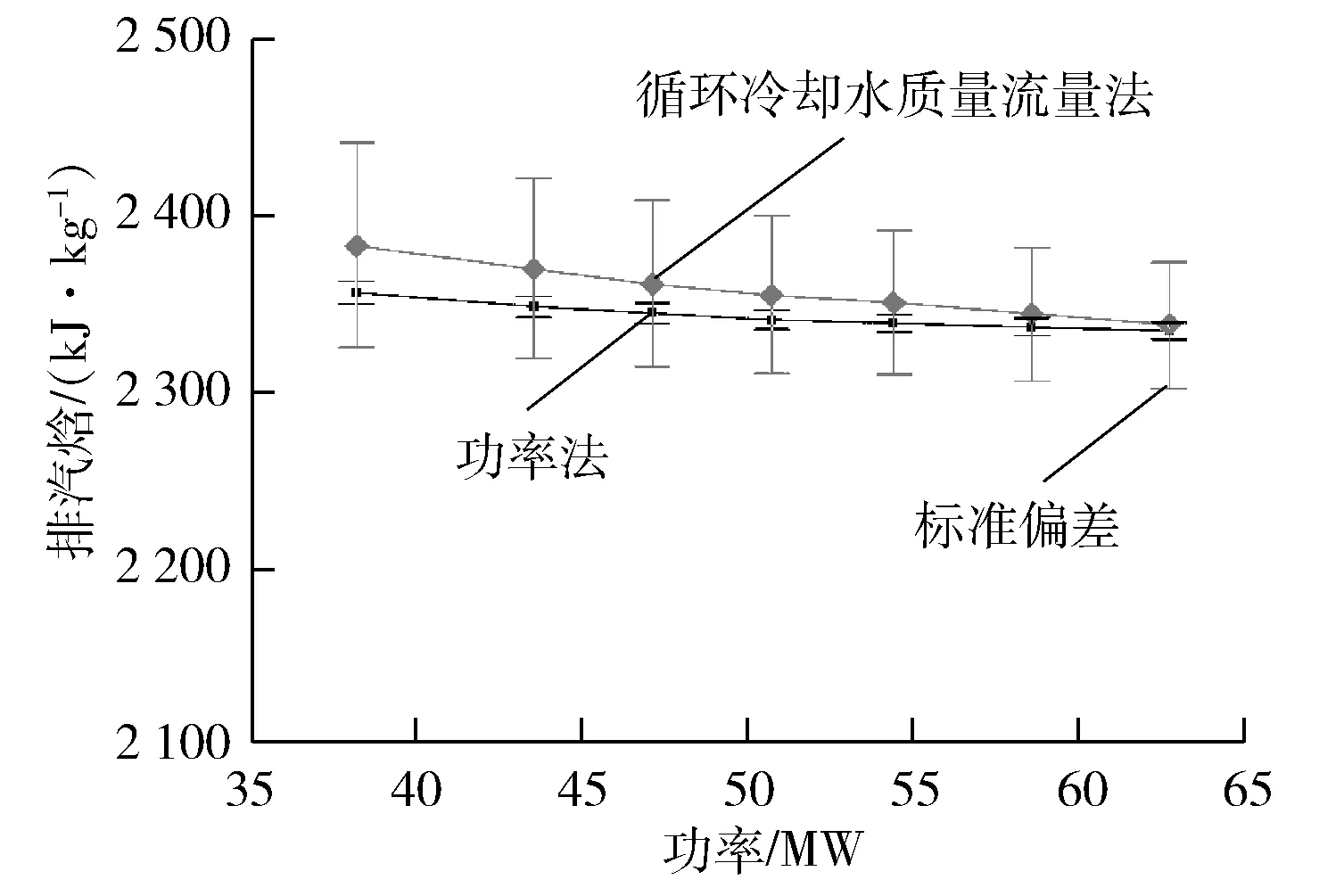
图8 排汽焓与标准偏差随负荷的变化
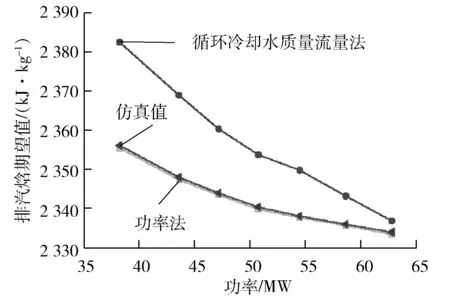
图9 两种方法计算的排汽焓期望值对比
在汽轮机负荷从38.19~62.73 MW的变工况过程中,排汽焓随负荷降低而增大,功率法计算得到的排汽焓与仿真值更吻合,其整体相对误差较小;凝汽器循环冷却水质量流量法计算得到的排汽焓与仿真值相差较大,且随着负荷的降低,该算法得到的计算结果偏离仿真值的程度越高。从误差带上来看,功率法计算的排汽焓误差带远远小于凝汽器循环冷却水质量流量法,前者宽度仅为后者的1/9,表明凝汽器循环冷却水质量流量法计算出的排汽焓不仅误差大,而且计算结果波动也大,功率法计算出的排汽焓更稳定,因此在机组变工况过程中,采用功率法计算排汽焓效果更佳。
两种方法计算出的排汽焓标准偏差均随负荷的减小而增大,原因在于测量仪表采样时均会带有测量误差,当被测对象的测量值在测量仪表量程的1/3~2/3处,测量结果最精确。在仪表量程范围内,被测对象测量值越小,则相对误差就越大,测量结果就越不精确;反之,被测对象测量值越大,则绝对误差就越大,对应的测量仪表引用误差也越大,测量结果也越不精确,所以仪表量程两端的区域测量可信度较低。实际电厂中,仪表的量程涵盖机组的负荷变化范围,运行人员通常将机组额定负荷设置在测量仪表最精确的量程处,故功率下降时,测量仪表显示被测对象偏离精度最佳量程处,所以计算结果表明排汽焓标准偏差增大。数据协调过程中,在仿真值中添加随机误差的时候,标准偏差不随机组负荷的变化而变化,所以标准偏差一定时,负荷越小,则随机误差值相对于仿真值越大,所以两种方法计算得到的标准偏差均随负荷减小而增大。
6 结语
笔者以试验数据和设计数据为依据,利用EBSILON软件对联合循环机组进行仿真建模,利用设计数据进行模型验证,模型数据与原始数据有良好的吻合性。经过数据协调模型的计算显示:各路流量相对均方根误差均有不同程度的下降,数据协调技术能够提高测量数据的准确性,具有一定的降噪能力。凝结水质量流量的精度提高最明显,从原来标准偏差为2.460 t/h降低到0.775 t/h,精度提高了68.5%。
基于测量仪表精度不同提出了功率法和凝汽器循环冷却水质量流量法计算排汽焓,并在机组变工况的情况下探究两个方法应用效果。对于精度要求比较高的排汽焓计算,若选取含有测量仪表误差标准偏差比较低的循环冷却水质量流量法,则计算结果会偏大;若采用含有测量仪表误差标准偏差比较高的功率法,则计算结果精度高。在无回热的燃气-蒸汽联合循环系统中,功率法计算排汽焓显现出较大的工程价值。

