六自由度机械臂的建模与MATLAB仿真

马宗家 石松泉

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.绍兴文理学院 机械与电气工程学院，浙江 绍兴 312000)

随着机器人技术的发展，机器人在许多行业有着广泛的应用.砌墙机器人作为建筑行业的新型设备，受到许多的科研人员的探索和研究.而机械臂作为机器人的执行部件，同样也是机器人课题研究中重要部分[1].其中，串联机械臂是应用最为广泛的机械臂，它是通过多个关节连接若干个连杆组成的一种具有多自由度的机制[2].为了了解机械臂关节和连杆之间的运动规律，探究机械臂各部位之间的位姿关系，需要对其进行运动学分析.通过机械臂的运动状态可以将其分为正运动和逆运动，正运动则是在确定机械臂的初始参数(连杆转角、连杆偏距、连杆长度)，通过关节角得到末端关节相对基坐标系的位姿，逆运动则是通过末端执行器的位姿来求得机械臂各关节角的参数信息[3].为了得到机械臂一般运动规律并减少设计周期，于是使用MATLAB对其进行建模，快速完成运动学分析及路径规划，为建筑机器人在实际作业中提供了理论数据支撑[4].

1 机械臂D-H模型的建立

本文研究的对象是拥有6个旋转关节的机械臂[5-6]，即6自由度机械臂.图1为三菱六轴机械臂的实物结构图，根据此类机械臂的特性，采用D-H参数法在各关节上建立D-H坐标系，得到机械臂D-H模型[7]，完整的关节坐标系模型如图2所示，其中是基坐标系的原点o0和第一关节坐标系原点o1相重合.图中D-H坐标系建立的步骤如下：

(1)坐标系zi-1的方向和机械臂关节i的轴向方向一致.

(2)坐标系xi的方向则是由相邻zi和zi-1的公垂线来确定.

(3)坐标系yi-1的方向是由zi-1和xi-1的叉积所得.

图1机械实物结构图

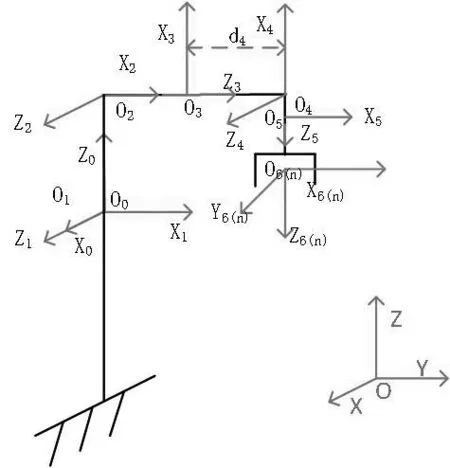
图2机械臂D-H坐标系

根据图2可以很直观推算出D-H参数表1中各参数的值，其中的θ为关节角，α为机械臂的连杆转角，a是相邻关节间连杆的长度，d则是相邻关节间连杆的偏移量[8].

表1 D-H参数表

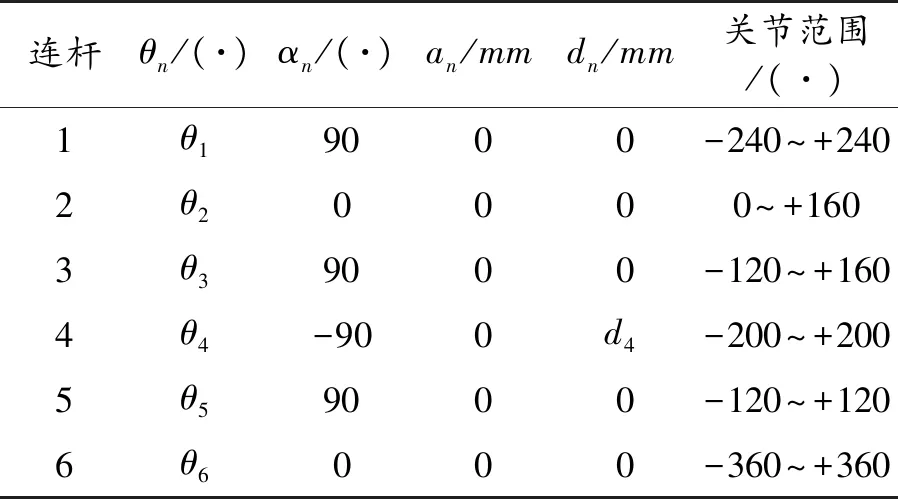
连杆θn/(·)αn/(·)an/mmdn/mm关节范围/(·)1θ19000-240～+2402θ20000～+1603θ39000-120～+1604θ4-900d4-200～+2005θ59000-120～+1206θ6000-360～+360

机械臂是由若干个关节通过刚体连接而成的开式运动链，因此要求得机械臂末端执行器相

对于基坐标的位姿[9-10]，需要求得各个关节之间的变换矩阵.因此将表1中的参数代入下列齐次变换矩阵[11]：

nTn+1=An+1=Rot(z,θn+1)×Trans(0,0,dn+1)×Trans(an+1,0,0)×Rot(x,αn+1)

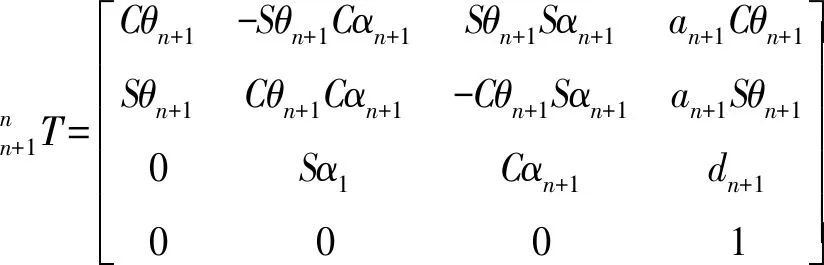
将表中D-H参数代入到公式(1)中，可以得到相邻关节间的齐次变换矩阵，得到矩阵如下所示[12]：

对得到的齐次方程依次进行相乘，最终得到基坐标相对于机械臂末端的变换矩阵：

T=T1T2T3T4T5T6=

式中：ci=cosθi，si=sinθi，cij=cos(θi+θj)，sij=sin(θi+θj)，其中变换矩阵T是求解机械臂六个关节的位姿的函数，通过T可以得到机械臂各关节的运动情况和末端姿态的关系.

2 六轴机械臂MATLAB仿真

2.1 机械臂建模

Robotics Toolbox是MATLAB专门用于机器人学的仿真工具包，为机器人的仿真提供了丰富的函数[13].其中Link函数和Serial Link是机械臂建模最重要的两个函数.在MATLAB的工作环境下，根据D-H参数表1，使用Link函数调用表中的参数就可以创建一个基于三菱机械臂仿真模型，具体指令如下所示.

L1=Link('alpha',pi/2,'d',0,'a',0);

L2=Link('alpha',0,'d',0,'a',0);

L3=Link('alpha',0,'d',0,'a',0);

L4=Link('alpha',pi/2,'d',0.2,'a',0);

L5=Link('alpha',-pi/2,'d',0,'a',0);

L6=Link('alpha',0,'d',0,'a',0);

robot=SerialLink([L1,L2,L3,L4,L5,L6]);

robotname='机械臂'；

theta=[pi/2 0pi/2pi/2-pi/2 0];

robot.plot(theta);

teach(robot);

图3示教控制模块的六个滑块分别对应着机械臂六个关节，通过移动滑块可以改变关节角，从而可以很直观地看到机械臂末端的位姿变化.

图3 示教控制板和机械臂模型

2.2 运动学正逆解仿真

关于机械臂正运动问题，可以调用Robotics工具箱中fkine函数进行求解[14].函数调用的格式为:T=R.fkine(Q),其中R表示机械臂模型，T为前向运动的正解，Q为机械臂六个关接变量值.取向量Q1=[pi/5 -pi/3pi/2 0 -pi/4pi/8]，代入fkine函数中进行运算，最后得到一个齐次变换矩阵如下：

对于逆运动学问题，则需要调用Robotics工具包中的ikine函数对其求解[15].函数调用的格式为:Q=R.ikine(T,Q0,M)，其中R同样是机械臂模型，T则是要进行逆解的齐次矩阵，Q0是为机械臂初始位置，M则是的逆解需要忽视的关节，本次实验使用的是六自由度机械臂，因此没有需要忽略的关节，只需要定义M=[1 1 1 1 1 1] .结合本次仿真模型，确定初始位置Q0=[0pi/2pi/2 0pi/2 0],并且确定机械臂末端Q2点的变换矩阵，矩阵如下所示：

随后调用ikine函数，最后可以得到相应的关节位置向量Q2=[0 0 0 0 0 0 ],同时将相应的齐次变换矩阵代入运动学逆解方程中，求得的关节角的大小与仿真解一致，确定了逆解方程的正确性.

2.3 机械臂轨迹规划

在robotics工具箱中研究机械臂的轨迹规划一般会使用jtraj或ctraj函数进行规划.这两种函数分别对应着两种不同的方法，其中jtraj主要应用于关节空间规划，而ctraj则是对应着笛卡尔空间规划.这两种方法都有各自的优点：关节空间的轨迹规划简单，算法运算量小，不易出现奇异方程.而笛卡尔空间规划的末端运动轨迹直观，便于观察机械臂运动状态[16].为了得到较好的仿真效果，本文机械臂同时采用两种方法进行轨迹的规划.

2.3.1 关节空间轨迹规划

jtraj是用于规划关节空间轨迹的常用函数，其调用的格式为[17]：[Q,QD,QDD]=jtraj(Q0,QF,T)，其中Q表示Q0点运行到QF点的运行轨迹，QD和QDD则是表达的轨迹规划的速度和加速度.Q0和QF显而易见的是机械臂运动的起始点和终点，T为给定的时间长度.假设本次仿真的时间为3秒，每次采集的时间间隔为50毫秒(即T=[0:0.05:2]).机械臂起点关节值Q1=[pi/5 -pi/3pi/2 0 -pi/4pi/8],终点关节值Q2=[0 0 0 0 0 0 ].在MATLAB环境下，将上面所得参数代入jtraj函数中运行，即可以求得各个关节的位置、速度、加速度的变化曲线[18].如图4所示.

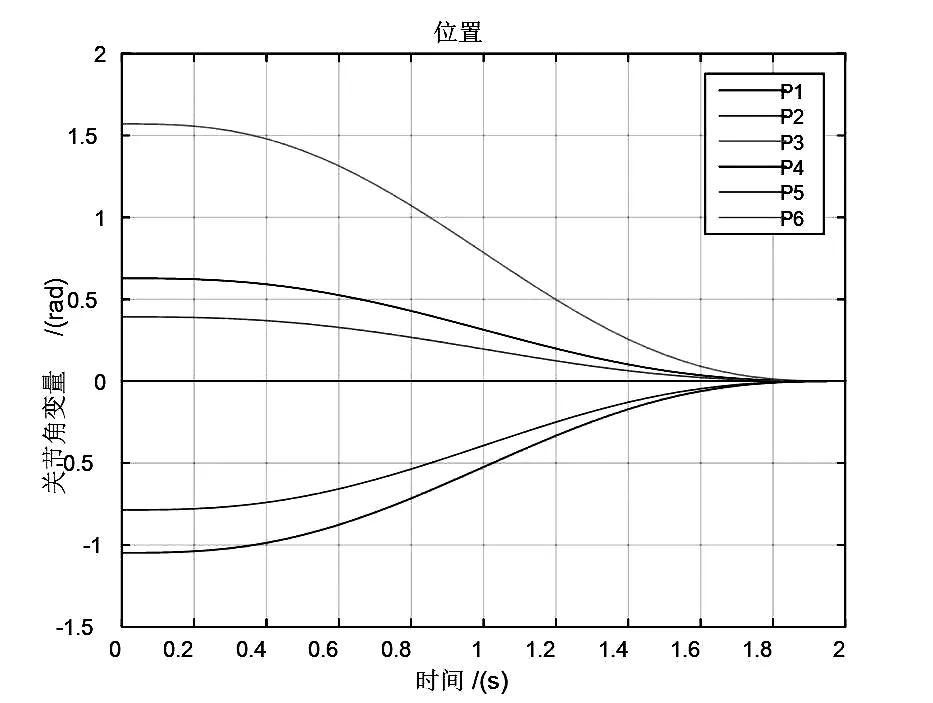
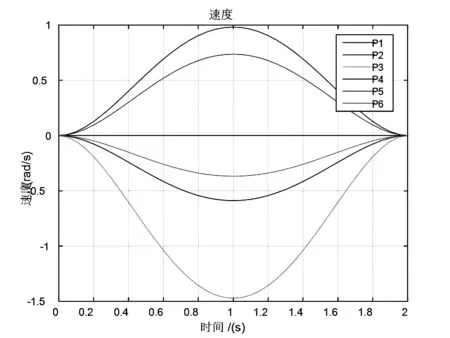
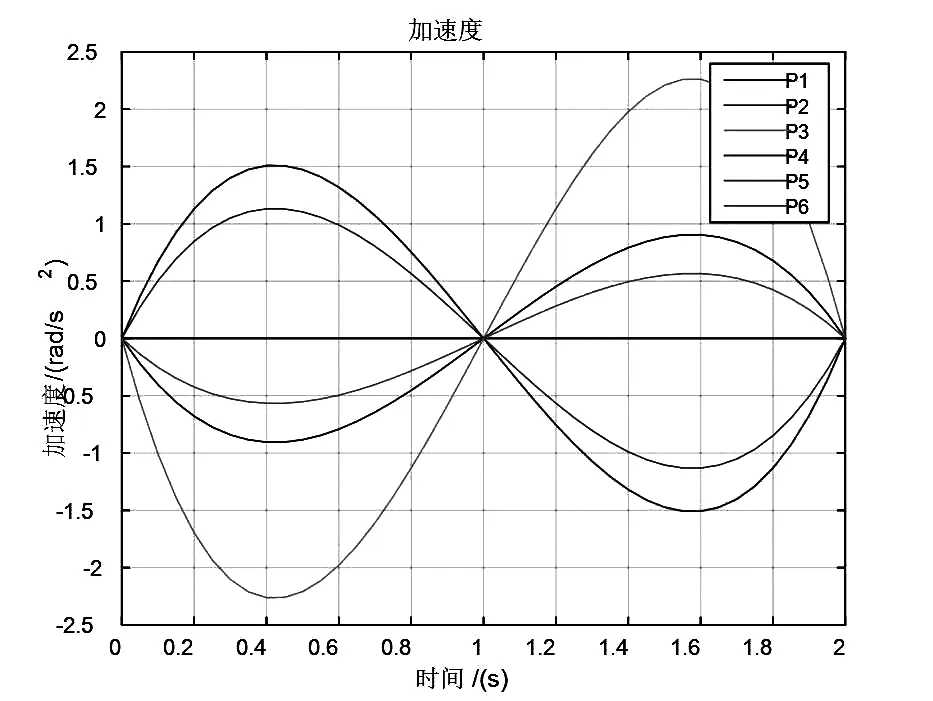
图4关节空间关节角、速度、加速度图

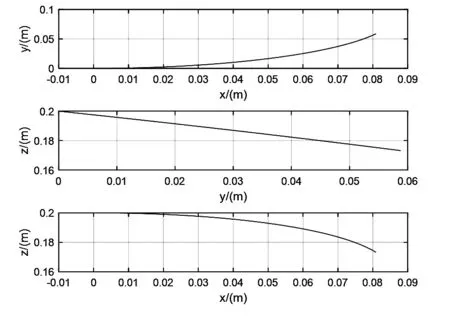
图5 末端轨迹在三个面上

2.3.2 笛卡尔空间轨迹规划

在实际控制机械臂的情况下，许多时候只需要机械示教到几个比较重要的点上，根据轨迹特征算出中间点，然后通过插补的方法进行精确的控制[20].对于笛卡尔空间可以使用TC= ctraj(T0,T1, N)函数进行规划，TC为函数返回的轨迹矩阵，T0和T1则分别为路径的起始点，N则是路径上的点数.本次仿真取空间Q1和Q2为例，将其代入函数中，进行笛卡尔路径规划，Q1，Q2的变换矩阵如图6、图7所示.

图6笛卡尔空间轨迹图

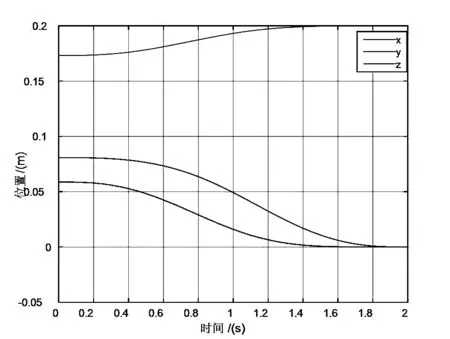
图7末端位置

通过结合两种空间规划路径的优点，在MATLAB中可以直观地看到机械臂末端的运行轨迹，也可以清楚了解到各个关节的位置，速度、加速度随时间变化的情况，通过上述数据可以为之后机械臂抓取砖块和躲避障碍物的研究奠定基础.

3 结论

本文研究的对象是一款来自于三菱公司的六轴机械臂，利用D-H法对机械臂各个关节坐标系建模，并且得到相应的齐次变换矩阵，并且通过理论推导，得到运动学正逆解方程.使用MATLAB Robotics工具箱建立机械臂仿真模型，并通过正逆运动检验了模型的正确性以及公式推导的准确性.机械臂在关节和笛卡尔空间下的轨迹规划仿真，得到各关节的角位移、角速度和角加速度曲线和机械臂末端在笛卡尔空间中的运行路径，为机械臂在建筑工业实际应用提供了理论参考.