多场耦合效应铁镓合金换能器的非线性模型

浮 翔，陈雪亮，徐卫星，杜金宇，张 冰

多场耦合效应铁镓合金换能器的非线性模型

浮 翔1，陈雪亮2，徐卫星1，杜金宇1，张 冰1

（1. 河南牧业经济学院，郑州 450011；2. 武汉船用电力推进装置研究所，武汉 430064）

本文基于热力学理论和J-A模型，建立了铁镓合金换能器的多场耦合非线性模型，利用此模型研究了铁镓合金换能器在不同温度和压应力下动静态输出应变及磁化强度与驱动磁场的关系。研究表明：随着铁镓合金换能器工作温度升高，铁镓合金换能器输出的最大应变减小；随着铁镓合金换能器的压应力增大，输出的最大应变增大，磁滞曲线面积减小，最大磁化强度减小，磁滞减弱。铁镓合金换能器的动态输出应变曲线为蝶形，且驱动磁场频率越高，输出应变越小，磁滞效应越明显。与实验结果对比发现，所建立的多场耦合非线性模型能够很好地描述铁镓换能器的实际工作状态，为磁致伸缩换能器的设计和发展提供了重要的理论依据。

铁镓合金换能器 多场耦合模型 压应力 温度效应

0 引言

磁致伸缩材料是一种新型智能材料，铁镓合金作为其中应用最广泛的一种，具有磁致伸缩效应明显、磁机转换系数高，韧性良好等特性[1]。铁镓合金换能器是以此材料为核心构成的一种将电磁能转化成机械能的装置，具有结构简单，输出功率大等优点，广泛用于超声探测、精密加工、金属探伤、以及无损检测等领域[2-3]。

铁镓合金换能器在实际工作中会表现出非线性的特性，同时多场耦合对换能器的影响也十分复杂，这就迫切需要建立铁镓合金换能器多场耦合的非线性模型对其特性进行描述。文献[4-5]分别建立了关于磁致伸缩材料的动态和静态磁滞模型，模型计算结果与实验测试结果较为吻合，但该模型未考虑温度场和应力场的影响。文献[6]基于热力学定律和磁滞效应，建立了超磁致伸缩材料磁-机-热耦合模型，分析了温度场对磁致伸缩材料应变和磁化强度的影响，但该文献仅通过静态实验验证了理论模型，缺乏动态实验的有效验证。文献[7-8]分别采用有限元方法计算了冷却水流场分布和换能器温度场分布，建立了磁致伸缩换能器多场耦合模型，同时考虑了换能器结构动力学原理，研究了动态磁滞效应的影响，然而这些模型没有考虑温度的影响。文献[9]建立了考虑应力和温度场的换能器输出模型，研究了温升对换能器的影响，表明温度是不可忽略的因素。文献[10]基于磁致伸缩材料多场耦合，建立了电磁场与机械场耦合模型，但缺少应力场对磁致伸缩材料输出应变的影响，没有真正实现系统层次的耦合。从以上文献可以看出，很少有模型从磁致伸缩换能器系统层次来描述其多场耦合的非线性。

本文从弹性Gibbs自由能角度出发，在热力学关系和Jiles-Atherton模型的基础上，建立了考虑多场耦合效应铁镓合金换能器的非线性模型，利用此模型模拟了铁镓合金换能器在不同温度和压应力下，动静态输出应变及磁化强度与驱动磁场关系。

1 铁镓合金换能器结构和原理

铁镓合金换能器的结构如图1所示。该换能器由铁镓合金棒（直径10 mm，长度90 mm，Fe83Ga17）、激磁线圈（由直径0.5 mm的漆包线绕制而成，匝数300）、永磁体、压力传感器（GZB-2型电阻应变式压力传感器）、输出顶杆（由不锈钢合金制成）、轭铁（由硅钢片叠制而成，主要起导磁作用）、预紧螺栓和弹簧等构成。

其工作原理为：在铁镓合金换能器的激磁线圈中通入交流电流，产生交变磁场，交变磁场通过轭铁传递到铁镓合金棒上，铁镓合金棒在交变磁场作用下沿径向产生伸缩变化，带动输出顶杆产生机械振动，从而完成电磁能向机械能的转变，实现位移和力的输出。通过调节预紧螺栓的松紧程度，来调整铁镓合金棒所受压应力的大小，通过压力传感器来测试所加压应力具体数值，铁镓合金棒在压应力的作用下会产生更大的磁致伸缩应变。永磁铁作用是提供一个恒定的偏置磁场，使铁镓合金棒的机械频率等于驱动磁场频率，避免“倍频”现象的产生。

图1 铁镓合金换能器结构图

2 考虑多场耦合效应的非线性模型

2.1 铁镓合金换能器的应变模型

磁致伸缩通常被等效为一个热力学系统来分析磁致伸缩材料复杂的磁-弹-热多场耦合关系，根据热力学定律可得单位体积的弹性Gibbs自由能为[11-12]：

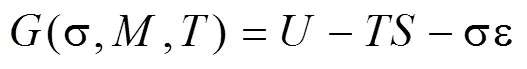
式中，为磁致伸缩材料单位体积的内能，为温度，为熵，为应力，为应变，为磁化强度。

根据热力学定律可以得到磁致伸缩材料的单位体积内能（,,）的全微分[13-14]：

结合式（2），式（1）的全微分：

由磁致伸缩材料应变与热力学关系可得：

将单位体积的弹性Gibbs自由能G(σ,M,T)在自由状态()=(0,0,0)处进行泰勒展开，参考点温度为0 K，得到多项式形式的弹性Gibbs自由能。

结合实验现象对式（7）各项的物理意义加以分析，可以认为铁镓合金的应变可以写成以下三部分：

第一部分由应力产生的应变eσ：

式中，E为弹性模量，为饱和磁致伸缩系数，为饱和磁化状态下的饱和应力。

第二部分由温度变化产生的热膨胀应变：

式中为磁致伸缩材料的热膨胀系数。

式中，是温度变化量，i()是与应力和温度差有关的系数。为了方便实际应用，取=2。则式（11）改写为：

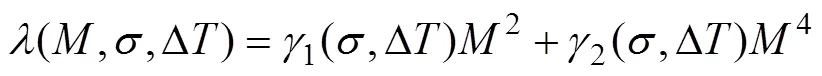
将gi(s,△T)进行泰勒展开得：

式中，是当=0时的关于应力的偏导数、是当=0时的关于温度的偏导数，保留关于应力温度的线性项，可得：

式中，11,12,13,21,22,23为材料的磁致伸缩系数，结合实验，通过测量不同应力温度下饱和磁化强度与饱和磁致伸缩得到一组齐次方程，求解结果如表1所示。

表1 磁致伸缩模型参数取值

因此，结合式(11)- (15)，整理化简便可得磁致伸缩(,,△)的表达式：

2.2 铁镓合金换能器的磁化强度模型

由J-A模型可知，有效磁场与无磁滞磁化强度之间的关系为：

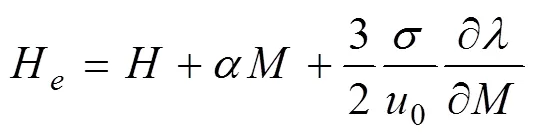
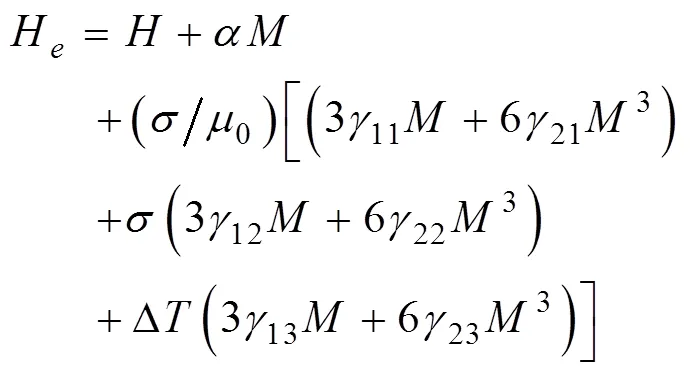
将(19)式简写为：

其中

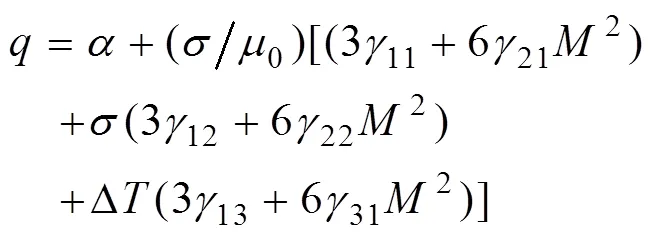
基于J-A模型假设[15-16]：

式中，是用来保证理论计算和铁镓合金物理特性一致的参数，是可逆因子。

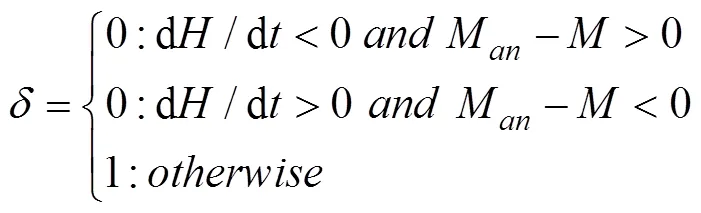
式(21)左右两边同乘以dH/dt，可得：

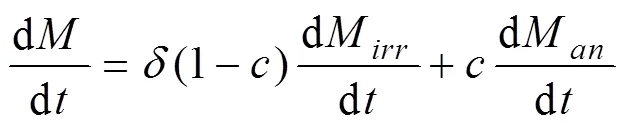
再结合复合函数求导法则，可得：

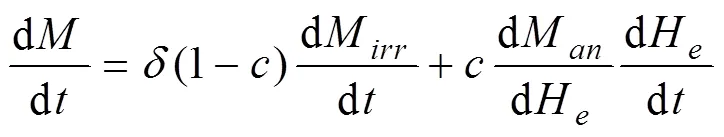
将式(20)对t求导并代入(23)，可得：

3 结果与分析

图2为铁镓合金换能器在不同温度下，利用多场耦合非线性模型计算的静态磁致伸缩应变与磁场强度的关系曲线。该换能器在静态工作的过程中，饱和驱动磁场强度约为50 kA/m，当驱动磁场小于此值时，磁致伸缩应变近似为线性变化；当驱动磁场大于此值时，磁致伸缩应变随驱动磁场增加而缓慢增大，最终趋于饱和。从图2可知，在环境温度一定时，铁镓合金换能器磁致伸缩应变随着驱动磁场的增加而增加。而当驱动磁场为定值时，磁致伸缩应变随着温度的增高而减小。产生上述情况是由于温度升高，热扰动对磁畴内磁矩的有序排列影响增大，但驱动磁场强度的增加不会削弱热扰动带来的影响。

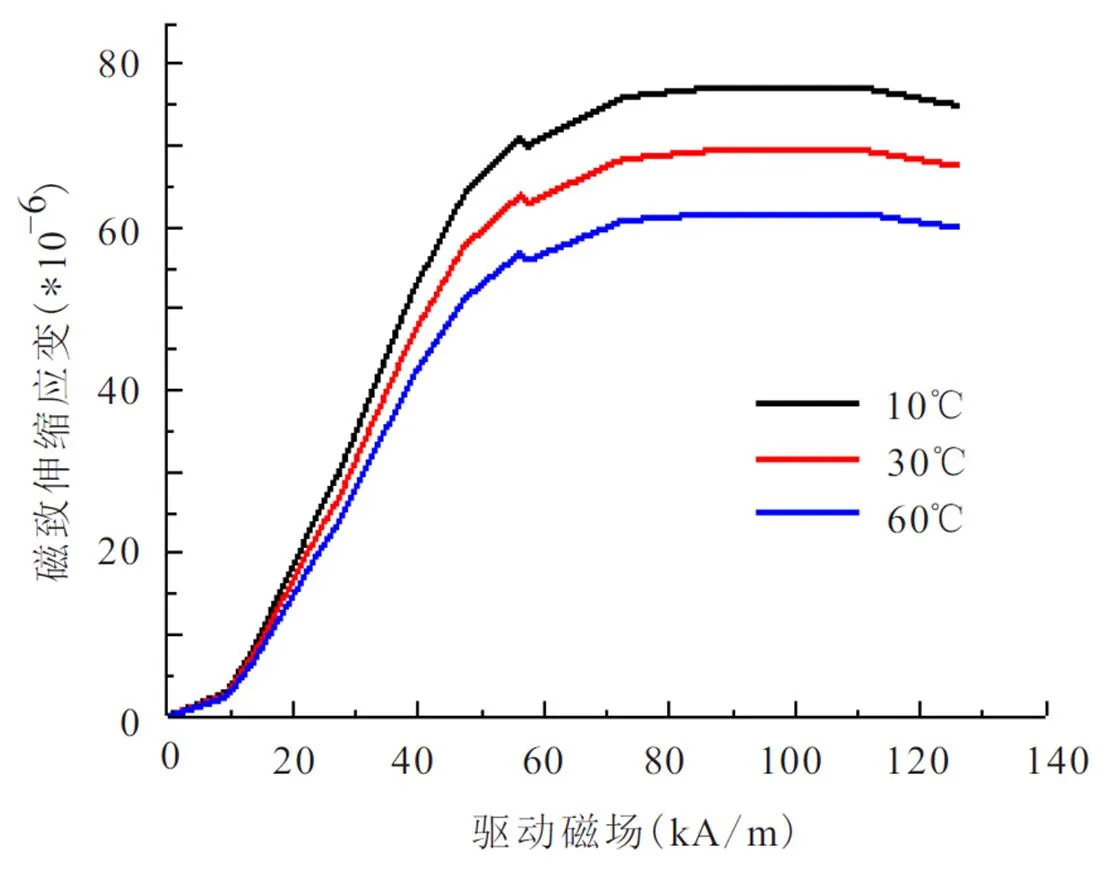
图2 不同温度下磁致伸缩应变与驱动磁场关系

图3为铁镓合金换能器在不同压应力作用下，利用多场耦合非线性模型计算的静态磁致伸缩应变与驱动磁场的关系曲线。由图可知，在正负驱动磁场作用下，磁致伸缩应变曲线的变化规律相同，都随驱动磁场强度的增大而增大，达到饱和驱动磁场强度后，增速放缓，趋于饱和，同时由于磁滞效应的影响，驱动磁场方向改变时，产生了小的回环。当压应力增大时，在相同驱动磁场强度下，铁镓合金换能器的磁致伸缩应变也相应的增加。说明压力使得铁镓合金中磁畴之间排列更紧密，在驱动磁场作用下可以产生更大的磁致伸缩应变，有利于提高该换能的输出功率。

图3 不同压应力下磁致伸缩应变与驱动磁场关系

图4为铁镓合金换能器在驱动磁场频率为50 Hz下，压应力分别为5 MPa，15 MPa，30 MPa，35 MPa作用下，利用多场耦合非线性模型计算的动态磁化强度与驱动磁场的关系曲线。由图可知：随着压应力的增加，铁镓合金换能器的磁滞曲线的形状不断被压缩，磁滞曲线的面积减小，饱和磁化强度值减小，而对应的饱和驱动磁场强度增大。从铁镓合金的导磁性角度分析，可知：在相同驱动磁场强度作用下，压应力越大，对应的磁化强度也越大；由磁导率的定义可知，压应力越大，铁镓合金磁导率越小，导磁性在下降。但施加较大压应力可以减小铁镓合金的磁滞效应，有利于减小磁场的滞后性，提高铁镓合金换能器工作的实时性。

图5为铁镓合金换能器在驱动磁场频率为50 Hz下，压应力为5 MPa时，利用多场耦合非线性模型计算的动态输出应变与驱动磁场的关系曲线。该动态输出应变曲线的饱和应变为40×10-6，所对应的饱和驱动磁场强度为12 kA/m，在驱动磁场增加和减小的过程中，对应不同的输出应变值，故形成了图示的蝶形回环，且在驱动磁场为零时，对应的输出应变非零，说明磁滞效应对铁镓合金换能器的影响较大。由图5可以看出，铁镓合金换能器的输出应变与驱动磁场关系曲线为蝶形曲线，模型有效地描述出了铁镓合金的动态磁滞特性，理论计算结果和实验结果吻合较好，偏差量不超过2.95%。与图4的静态曲线对比可知，驱动磁场的磁场频率越高，所产生的最大磁致伸缩应变值就越小，磁滞效应也越明显。图5描述了换能器的整体输出应变和驱动磁场之间的关系，图中的星号是实验测试的数据，实线是模型计算出的结果，可以看出两者吻合较好，说明了所建立的考虑多场耦合的非线性模型能够准确描述铁镓合金换能器动态运行的特性，能够描述换能器的真实运行情况。

图4 驱动磁场频率50 Hz的磁化强度与驱动磁场关系

图5 驱动磁场频率50 Hz输出应变与驱动磁场的关系

4 结论

为了研究铁镓合金换能器实际的工作情况，本文基于热力学理论和J-A模型建立了考虑多场耦合效应铁镓合金换能器的非线性模型，运用此模型分析了铁镓合金换能器在不同温度和压应力情况下，动静态输出应变和磁化强度与驱动磁场关系，模型计算结果与实验吻合，能够真实有效反映实际情况。

1）温度和压应力对铁镓合金换能器的输出应变有较大影响，温度越高对应的输出应变越小；压应力越大，对应的输出应变越大。动态的输出应变曲线为蝶形，且驱动磁场频率越高，输出应变越小，磁滞效果越明显。

2）压应力越大，铁镓合金换能器的磁滞曲线面积越小，最大磁化强度的值也越小，磁滞越弱。

[1] 张纳, 王博文, 王莉等.磁致伸缩、压电层状复合磁电传感器非线性动态有限元模型[J]. 电工技术学报, 2012, 27(7): 146-152.

[2] Huang W, Li Y, Weng L, et al. Multifield Coupling Model With Dynamic Losses for Giant Magnetostrictive Transducer[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4):1-5.

[3] Cao S, Yang S, Zheng J, et al. An Equivalent Circuit Model and Energy Extraction Technique of a Magnetostrictive Energy Harvester[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4):1-6.

[4] Calkins F T, Smith R C, Flatau A B. Energy-based hysteresis model for magnetostrictive transducers[J]. Magnetics, IEEE Transactions on, 2000, 36(2): 429-439.

[5] Xu H, Pei Y, Fang D, et al. An energy-based dynamic loss hysteresis model for giant magnetostrictive materials[J]. International Journal of Solids and Structures, 2013, 50(5): 672-679.

[6] Ke Jin, Yong Kou, Xiaojing Zheng. A nonlinear magneto-thermo-elastic coupled hysteretic constitutive model for magnetostrictive alloys[J]. Journal of Magnetism and Magnetic Materials, 2012(324): 1954-1961.

[7] 曾海泉, 曾庚鑫, 曾建斌等. 超磁致伸缩功率超声换能器热分析[J]. 中国电机工程学报, 2011(6): 116-120.

[8] 金亮, 寇晓斐, 郭富坤等. 基于电磁超声换能器的铁磁材料电磁声发射检测方法[J]. 电工技术学报, 2017, 32(18): 98-105.

[9] 曾建斌, 白保东, 曾庚鑫, 曾海泉, 李永建. 考虑压力变化的超磁致伸缩超声换能器动态模型[J]. 电工技术学报, 2012, 27(10): 216-219.

[10] Jin K, Kou Y, Liang Y, et al. Effects of hysteresis losses on dynamic behavior of magnetostrictive actuators[J]. Journal of Applied Physics, 2011, 110(9): 093908(1-7).

[11] Li Wang, Bo Wen Wang, Zhi Hua Wang, Ling Weng, Wen Mei Huang, Yan Zhou. Magnetothermome-chanical characterization of giant magnetostrictive materials[J]. Rare Met. 2013, 32(5): 486-489.

[12] Jiles D C. Theory of the magnetomechanical effect[J]. Journal of Physics D Applied Physics, 1995, 28(8): 1537-1546.

[13] Jiles D C. Modelling the effects of eddy current losses on frequency dependent hysteresis in electrically conducting media[J]. Magnetics, IEEE Transactions on, 1994, 30(6): 4326-4328.

[14] Iyer R V, Krishnaprasad P S. On a low-dimensional model for ferromagnetism[J]. Nonlinear Analysis: Theory, Methods & Applications, 2005, 61(8): 1447-1482.

[15] Bottauscio O, Roccato P E, Zucca M. Modeling the dynamic behavior of magnetostrictive actuators[J]. Magnetics, IEEE Transactions on, 2010, 46(8): 3022-3028.

[16] Slaughter J C, Dapino M J, Smith R C, et al. Modeling of a Terfenol-D ultrasonic transducer[C]. SPIE's 7th Annual International Symposium on Smart Structures and Materials. International Society for Optics and Photonics, 2000: 366-377.

Nonlinear Model of Multi Field Coupling Effect of Fe-Ga Alloy Transducer

Fu Xiang1, Chen Xueliang2, Xu Weixing1, Du Jinyu1, Zhang Bing1

(1. Henan University of Animal Husbandry and Economy, Zhengzhou 450011, China；2. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)

TB552

A

1003-4862（2019）09-0023-05

2018-11-28

河南省科技攻关项目（182102210322），河南省高等学校重点科研项目(16A480002)

浮翔（1987-），男，讲师。研究方向：新型材料与器件。E-mail: 3546470@qq.com