基于数据挖掘的电网故障关联规则的研究∗

彭 刚 唐松平 曾 力 肖 云

（广东电网有限责任公司惠州供电局 惠州 516000）

1 引言

电网系统是现代社会维持正常运转的重要生命线。而分散的电网系统在各种动态的环境下，不可避免的受到设备故障、接触动物，树木，雷击等各种影响造成停电事故［1～3］。如何快速地进行故障诊断和系统恢复，已成为确保电网系统可靠性研究的方向［4］。为了提高点完后系统的可靠性，电力管理系统需要对停电做出正确迅速的反应。然而，由于安全原因，许多电力公司在发现故障原因之前不能及时修复故障。整个修复过程可能需要几十分钟到数小时，维修人员往往需要沿输电线路搜寻几十公里，试图找到故障的原因。例如，可能由雷击造成的输电线灼烧痕迹，死亡的动物尸体悬挂在输电线上，更有倒下的树木毁坏输电线路等现象［5］。

现有文献已经研究了许多不同的方法来定位故障［6～8］。有效的故障原因识别也可以提供有价值的信息来缩小搜索区域，从而加快恢复和提高系统的可靠性。例如，调度中心可以告知救援车辆集中于某些类型的故障原因，甚至派遣相应人员早较早的恢复系统。电网系统故障原因识别可以看作是一个分类问题，在某种意义上，运营商试图将已报告的故障分类为现有故障原因类中的一个，这些故障类已经由专家精心设计。随着数据挖掘技术的发展，大量的研究已经证明了数据挖掘方法在电力系统中应用的有效性［9］，可利用历史电网停电数据提取故障模式。然而许多停电数据不平衡，难以满足供电部门及时根据停电数据挖掘出故障的真实原因。

本文首先介绍了基于数据挖掘的模糊分类E-算法，同时根据广东省电网故障原因选取了7个地区作为研究对象，并给出了故障原因识别方案。最后验证了算法在故障原因识别中的性能，并与人工神经网络（ANN）进行了比较。

2 数据挖掘E-算法

2.1 模糊集和模糊规则

模糊分类系统有两个关键要素［10］:模糊集和模糊规则。模糊集可以通过其隶属函数得到充分的定义；模糊规则提供了类的推理能力和推理机制。

假设一个含有K规则、m输入和n输出的模糊分类系统，在本文中，只考虑单个输出属性的情况，即n=1，K规则表示为

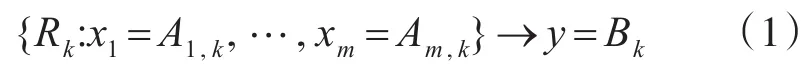
其中，k=1,…,K，Am,k（i=1,…,m）是规则 Rk中输入属性xi的模糊集，Bk是规则Rk中输出属性y的模糊集，则模糊规则也可以用向量形式表示。

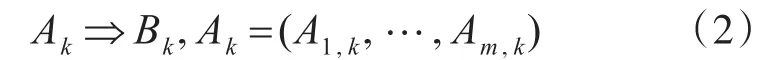
2.2 支持度和可靠度

数据挖掘中的关联分析［11］主要是探究关联规则X=Y的属性之间有意义的关系（本文只考虑一个结果属性）。关联规则与模糊规则具有相同的格式，并且它们满足前部分X的数据也可能满足结果部分Y。

支持度［12］是指前项属性 Xk（k=1,…,K ，K是关联规则的数量）与后项属性Yk在一个数据集中同时出现的频率。信任度［13］是指前项属性Xk发生时，后项属性Yk发生的概率。

其中，P(⋅)为概率算子。

基于规则的数据样本相容性等级将这两个度量运用到模糊规则中，即 Xl与第k个规则的相容性等级表示为［14］

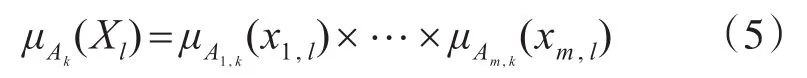
其中，Xl=(x1,l,…,xm,l)表示第l个数据样本，l=1,…,N，N表示数据样本的总数，m表示每个数据样本中的属性的数量，μA1,k(xi,l)，l=1,…,m表示属性xi,l相对于规则Rk模糊集Ai,k的隶属关系。

支持度标准化［15］的模糊向量表示Bk类数据基于第k个规则的相容性等级标准和与数据样本数之比:

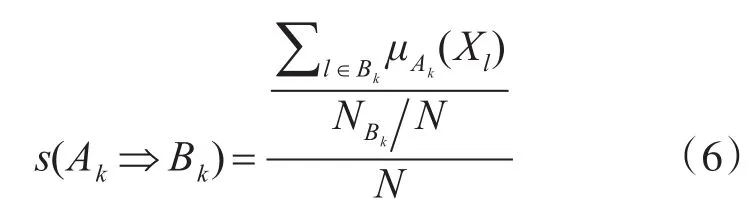
置信度的标准化［16］的模糊向量表示Bk类数据基于第k个规则的相容等级标准和与基于第k个规则的所有数据样本的相容等级之比:

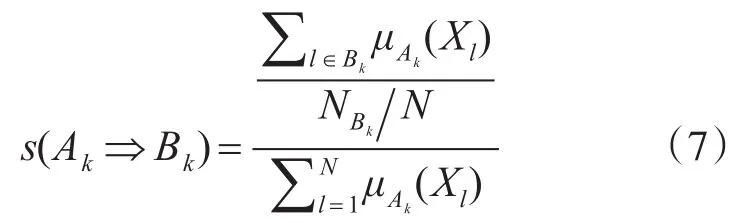
2.3 隶属函数

由于每个属性的模糊集合分类是未知的先验假设，E-算法同时为每个属性使用四个模糊集合分类，如图1所示。其结果是每个前项属性首先与由这四个分类生成的14个模糊集以及一个特殊集（即总共15个）相关联。

图1 每个属性隶属函数的四个模糊划分

2.4 模糊规则

E-算法首先枚举前项模糊集的所有可能组合，然后将每个组合赋值给后项部分生成规则，所有这些规则形成初始规则种群。由于每一个前项属性对应于15个可能的模糊集，属性m的模糊集合的可能组合数为15m，即呈指数增长，为了减少计算需求，只生成小于或等于三个前项属性的规则。如式（5）所示，兼容性级别是几个数值的乘积。隶属度值规则所包含的隶属度值可以用规则计算数据样本的相容性等级。因此，只有在逻辑上包含较短的规则才能降低计算需求，同时保持合理的性能。

每一个前项模糊集的组合对应一个模糊规则，一旦其结果被指定，其结果取决于式（8），即给定模糊集合组合的最大置信值的类被赋值为规则结果。

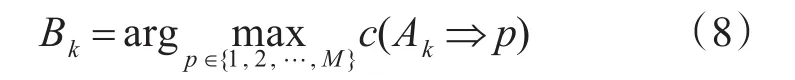
其中，M表示分类的总数。E-算法进一步将每个规则作为规则权重分配给确定的CFk等级。确定性等级是给定Ak的最大置信值和第二最大置信值csec之间的差值:

其中，csec=maxq∈{1,…,M};q≠pc(Ak⇒ q)。通过初始规则种群的试验和错误选择每个类的用户定义的数字规则（在本文中，Ns=30），使用 s(Ak⇒Bk)和c(Ak⇒Bk)的乘积作为度量。这些规则形成了从数据中提取出来的模糊分类规则库，并负责分类任务的决策。

2.5 模糊分类

当在测试数据上实现模糊分类任务时，采用单一优胜规则方法，对于任何测试数据Xr，从模糊分类规则库中选择一个规则，该规则将相容性等级的最大乘积与测试数据Xr和确定等级CFk划分。

3 电网系统故障识别

3.1 数据选择

在本文中，广东省电网故障数据用来说明故障原因识别。由于保护装置（例如断路器、熔断器）的激活，检测广东省电网分布系统中的故障，则将相关信息记录到数据收集系统中。每次停电记录由33个信息域组成，其中六个信息域被认为是统计显著性检验的建议中最重要的因素。这六个信息域是电路ID、天气、季节、时间、相位影响和保护装置激活。机组人员在恢复过程中输入的属性原因记录了故障的实际根源，并用作类标签。在本文中用于说明客观故障原因分为三个主要方面:树木，动物接触和雷击。

基于专家建议和不同地理特征的考虑，在广东省的21个地级市选取7个地区作为研究对象:广州（GZ）、深圳（SZ），珠海（ZH）、佛山（FS）、东莞（DG）、汕头（ST）和惠州（HZ）。

3.2 故障原因识别方案

所有选择的分类变量分为六个因素，如表1所示。

表1 各影响因素的要素综述

运用似然测度将分类变量转换为数值变量，即需要将数值输入确定到先前不同的模糊集属性的模糊隶属度中，以满足变量可以使用E-算法进行计算。

式（10）所示的可能性度量代表在某个条件下，发生故障造成的停机的条件概率。

其中，i代表故障类型，j代表影响因素，Ni,j代表在条件 j下引起的故障i的停机次数，Nj代表在条件 j下引起的停机次数，Li,j代表在条件 j下引起的故障i的可能性度量。

似然测度可以为故障原因识别提供有用的信息，它在逻辑上可以用作E-算法的输入值。然而，似然测度依赖于故障类型i和影响因素 j。相同的数据映射到不同故障原因得到不同似然测度集合，即使在相同影响因素下同样适用。这意味着似然测度随故障原因而变化。图2所示的电网故障原因识别方案由三个相同的支路组成:树木、动物和雷电。每个分支标识其指定的故障原因，也可以扩展以识别更多的故障原因。

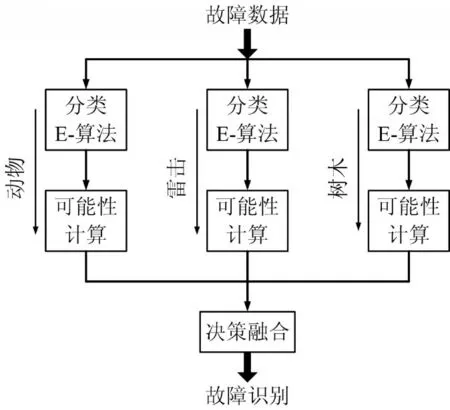
图2 配电故障原因识别原理图

在每个分支中，故障数据首先由似然计算模块进行转换，然后将生成的似然测度传递给分类模块，其中应用E-算法确定输入故障的类。由于每个分支只负责指定的故障原因，所以它面临一个二进制分类任务。由于故障原因造成的停电次数可能只占故障原因多样性的一小部分（由树木引起的故障、动物引起的故障和雷击故障的比例）。

决策融合模块将不同分支的结果组合成最终的分类决策。当不同的分支达到一致的故障原因估计时，决策融合模型可以做出简单的决策。当冲突的结果偶尔发生时，该模块将测试数据的相容等级与每个分支进行比较，以确定故障原因。

4 实验分析

4.1 实验准备

本文采用的是2004年至2012年广东省电网故障数据。在每个代表地区数据按年划分为训练数据和测试数据:从2004年到2009年的故障数据用作训练集，其余数据作为测试集。表2显示了各地区的数目、动物和雷电造成的电网故障率。

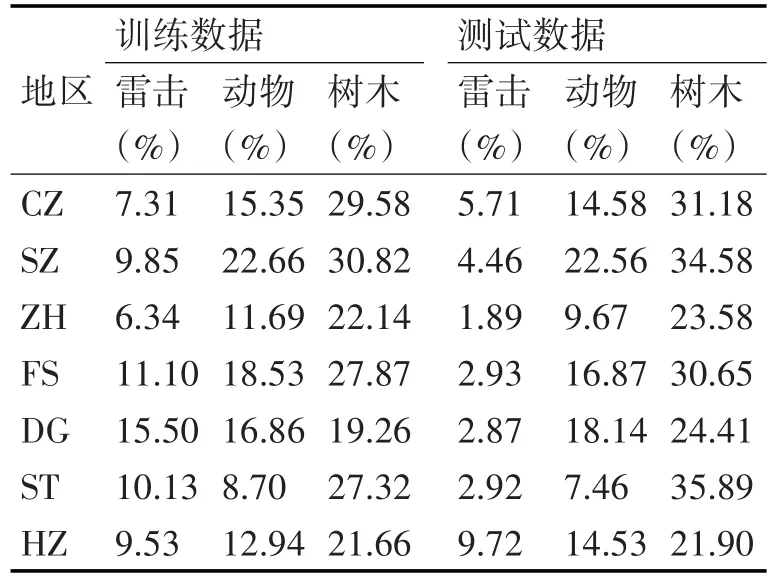
表2 不同地区的树木、动物和雷电造成的电网故障

在训练数据中，雷电引起的故障占9.97%，测试数据占4.36%。在其测试数据集中，ZH地区只有1.89%的电网故障是由雷电引起。动物造成的故障在训练数据中占15.25%，在测试数据中占14.83%。树木引起的故障是最大的故障类别。在训练数据集中，树木引起的平均故障率为25.52%，测试数据为28.88%。与雷电和动物引起的故障相比，树木引起的故障和非树故障造成的故障相对比较平衡。

4.2 性能测试

当数据不平衡时，使用传统测度对整体分类精度会产生影响。若考虑两类不平衡数据集，假设95%的数据来自大多数的类，而只有5%的数据来自少数的类。那么分类器盲目地将每个数据归类到各自的类中，在不处理数据的情况下可达到95%的整体精度。运用g-mean来评价数据集的分类性能可以有效避免不平衡数据带来的分类结果误差。g-mean是由混淆矩阵组成，假设由树木、动物和雷电引起的故障是正类，对应的不由这些因素引起的故障为负类，如表3所示。

表3 混淆矩阵

正确率Acc+=TP/(TP+FN)表示正类的分类精度，而错误率Acc+=TN/(TN+FP)表示负类的分类精度。g-mean检验正负类的分类精度，并对两者之间的巨大差异进行判断，数学表达式为

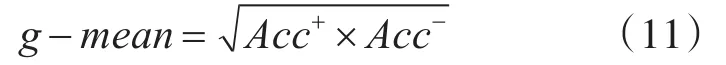
4.3 结果分析

运用基于g-mean的E-算法和ANN算法分别计算雷电、动物、树木造成的故障测试数据，结果如图3～图5。ANN算法的性能基于30个运行结果表明:在95%置信区间，竖条的高度表示平均值。由于E-算法的确定性结果为Nn，在模糊分类规则库中包含的规则数量已经确定。

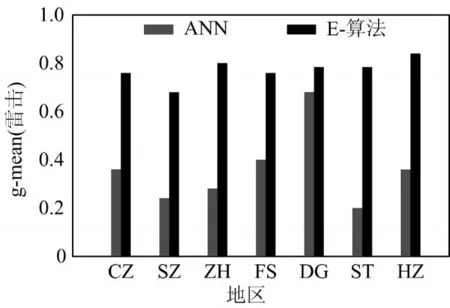
图3 雷击引起的故障识别g-means

图3 表明，在识别雷电引起的故障时，E-算法在g-means中具有显著的优势。在ST地区中，E-算法平均的g-mean值超过ANN算法的271%。在表4中，所有7个地区的“雷电引起的故障”假设的单样本检验的P值小于0.05。因此，零假设被拒绝，接受备选假设。可以得出E-算法的g-mean比ANN的平均g-mean大。尽管在所有七个选择地区中，E-算法在雷电引起的故障中始终比ANN表现得更好，但对于其他两个故障原因，不能得出类似的明确结论。

图4 动物引起的故障识别g-means

图4 表明，在5个地区内由动物引起的故障，E-算法的g-mean值比平均g-mean值大，但在两个地区中较小:SZ和FS。假设的单样本检验也表明，在5个地区中，E-算法优于ANN算法。而对于FS地区，ANN算法比E-算法有更大的g-mean值。

图5表明，在四个地区中由树木引起的故障，E-算法有较大的 g-mean，而 CZ、SZ和 HZ的g-mean值较小。

图5 树木引起的故障识别g-means

在实验数据中也对假设进行了单样本检验，以比较E-算法和ANN算法的g-mean:

式（12）是基于测试P值进行的零假设，可得到实验数据的概率。当P值小时，则会拒绝零假设。本文选用显著性水平0.95，则P值小于0.05，拒绝零假设，选择备择假设。表4给出了E-算法和ANN算法所实现g-mean单样本检验的P值。

表4 对假设检验的P值g-means采样

表4中假设单样本检验结果表明，E-算法在四个地区优于ANN算法，在SZ和HZ中得到更小的g-mean值。

5 结语

有效的电网故障原因识别有助于加快恢复电力供应，提高配电系统的可靠性。然而，许多现实数据不平衡问题常常影响到故障原因识别的性能，尤其是对少数类原因的识别。本文针对不平衡数据，利用模糊分类E-算法计算电网故障数据并进行原因识别。为了验证本研究所提出方法的有效性，将该算法与人工神经网络（ANN）进行对比。结果表明:当故障数据是不平衡时，本研究算法可以实现更好的性能。