Cooperative guidance of seeker-less missile considering localization error

Jinbo ZHAO, Shuxing YANG, Fenfen XIONG

a School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China

b Xi’an Modern Control and Technology Institute, Xi’an 710065, China

KEYWORDS

Abstract To perform an accurate fire-and-forget attack of seeker-less missile with the consideration of the localization error, a new cooperative guidance strategy of multi-missiles is proposed in this work. Firstly, an estimated position of the seeker-less missile is carefully selected, based on which the slant angle of the line between the estimated and real positions of the seeker-less missile is approximately derived inspired by the localization theory of GPS (Global Position System).Then,respectively based on the guidance law considering the impact angle and time constraints,the consensus theory and the finite-time convergence approach, three cooperative guidance laws employing the previously obtained slant angle are derived for intensive attack to address either a stationary or maneuvering target.Simulation results well demonstrate the effectiveness and advantages of the proposed cooperative guidance strategy.

1. Introduction

Much research in recent years has focused on the homing guidance system as it can achieve fire-and-forget attack.1With the development of control theory, a great number of terminal guidance laws relevant to the homing guidance have been proposed,2-6such as the impact-time-control guidance laws employing the Liapunov stability theory,optimal control,slide mode control, feedback linearization, et al. In order to implement the guidance laws for homing guidance, the seeker can provide a significant input,while its cost is extremely high(commonly account for more than 1/3 of the total cost of missile). Therefore, it is necessary to study the guidance of the seeker-less missile.

The external guidance approach1is commonly employed for a seeker-less missile, in which a ground station is utilized to control the trajectory of the seeker-less missile, and thus the fire-and-forget attack cannot be implemented.7,8Alternatively, the cooperative guidance of multi-missiles, widely employed to enhance the penetration capability,9-13has been considered to perform the fire-and-forget attack of the seeker-less missile,14,15in which the seeker-less missiles are guided by a missile with seeker. However, for the works in Refs.14,15, all the missiles require highly accurate localization information to achieve precise attack, which significantly increases the operational cost.

Therefore, a new cooperative guidance strategy for multimissiles is proposed in this work to guarantee that the seeker-less missile can implement accurate fire-and-forget attack even if a position estimation error exists, with the assumption that the measurement error of the velocity for the seeker-less missile can be neglected during the terminal guidance. Firstly, partly inspired by the localization theory of GPS (Global Position System), the estimated position of the seeker-less missile is carefully determined to obtain the slant angle of the line between the estimated and real positions of the seeker-less missile that is a prerequisite to implement the cooperative guidance. Then, based on the previously derived slant angle,a new cooperative guidance law for stationary target is proposed by employing the commonly used guidance law considering impact angle and time constraints. Meanwhile, to address maneuvering target,another two cooperative guidance laws are designed based on the consensus theory and the finitetime convergence approach, respectively. The proposed three cooperative guidance laws ensure that the real position of the seeker-less missile is always located on the line between the estimated position and target, and the estimated position of the seeker-less missile can accurately reach the target as well.Therefore, the seeker-less missile could attack the target precisely even the position estimation error between its real and estimated position exists.In addition,all the proposed cooperative guidance laws can implement intensive attack, i.e. multiple missiles hit a single target during a short period of time,which can induce the saturation of the defensive system of the target so as to improve the penetration capability of missiles.

The rest of this work is organized as follows. In Section 2,the many-to-one missile-target interception engagement is presented along with the description of the basic research problem of this work. In Section 3, the proposed cooperative guidance strategy is introduced, based on which the cooperative guidance law is derived for the stationary target. In Section 4,another two cooperative guidance laws are proposed for the maneuvering target. Simulation results are presented and analyzed in Section 5. Conclusions are draw in the last section.

2. Basic problem formulation

In this work, the case that multiple seeker-less missiles Mi(i=1, 2, ... , n) guided by a missile with seeker (Ml) attack a stationary or maneuvering target T is considered.The centralized leader-follower framework(shown in Fig.1)is employed,in which the missiles with and without seeker are regarded as the leader and followers, respectively.

Fig. 1 Centralized leader-follower framework.

The following three assumptions are made to simplify the guidance problem as is commonly done in literature: (A) missiles and target are all regarded as mass points in the yaw plane; (B) compared with the characteristics of the guidance loop, the dynamic lag of autopilots can be ignored; (C) the acceleration of the maneuvering target can be accurately derived by the high-performance seeker of the leader.14

In addition, it is assumed that all the followers employ the same form of guidance law, and thus only one of them Miis taken as an example for illustration. Therefore, the guidance geometry of the leader, follower Miand target in the inertial reference coordinate X-O-Y is shown in Fig. 2. The variables with subscripts i and l respectively represent the states of the follower Miand leader (or their states relative to the target),and the variables with subscripts T and il respectively represent the states of the target and the relative motion states between the leader and follower Mi.Moreover,v，a，θ，q and r denote the speed, normal acceleration, heading angle, Line-of-Sight(LOS) angle, and LOS distance, respectively.

According to Fig.2,the relative kinematics equations of the leader-target and follower-target are respectively given as follows.

Moreover, the relative kinematics equations between the leader and follower Miare given as below:

3. Proposed cooperative guidance strategy

The leader with a seeker can measure its motion states relative to the target(e.g.the LOS angle rate ˙ql),so as to implement the precise attack via certain common guidance approach. However, the position of the follower Mican only be measured by the localization system such as INS/GNSS(Inertial Navigation System and Global Navigation Satellite System) aswith measurement error.That is to say the motion states of follower Mirelative to the target cannot be accurately derived,which indicates that the common guidance approach cannot be directly applied to the follower.

Fig. 2 Guidance geometry among the leader, follower Mi and target.

Therefore,a new cooperative guidance strategy is proposed to guarantee that the seeker-less missile can implement the precise attack even position estimation error exists. Although the seeker-less missiles with the leader cannot ensure a same attack time,intensive attack can be achieved,which can also improve the penetration capability of missiles. Within the proposed cooperative guidance strategy, an initial estimated position of the followeris firstly elaborately selected, based on which the slant angle of the line between the real(Mi)and estimatedpositions is approximately derived. Moreover,since the measurement error of the velocity vican be neglected during the terminal guidance,the velocities of the real(Mi)and estimatedpositions of the follower are identical. It indicates that the aforementioned slant angle can be considered to be constant, which thus is only required to be available at the initial time. Then, based on the previously derived slant angle,several cooperative guidance laws addressing stationary and maneuvering target are designed to ensure that the real position Mi(denotes the real position of the follower Mifor brevity)can always lie on the line segment betweenand target(),which means that even if an error exists between the estimatedand real(ri)LOS distance of the follower Miand target,there is no error between the estimatedand real(qi)LOS angle. Therefore, the seeker-less follower Miwith position estimation error between its real and estimated positions can still attack the target precisely, as long as its estimated positioncould reach the target(as shown in Fig.3).In this case, the position error between Miandwould only influence the impact-time estimation for follower Mi. In addition,the intensive attack is also considered in the cooperative guidance law.

Overall,to implement the accurate attack of seeker-less follower Mivia the proposed cooperative guidance strategy, it is required that:

3.1. Calculation of slant angle of

Fig. 3 Relative motion among ， Mi and the target.

As the constant slant angle of the line between the estimated and real positions of the seeker-less missile is merely required to be calculated at the initial time, only the initial status are studied in this subsection. In Fig. 4, since the measurement error of INS/GNSS is generally limited within a certain range,the real position Mican be limited within the circle with the measured positionas the center and Δ as the radius. Note that the LOS distance rilcan be estimated by the data link equipped on missiles.16Therefore, the real position Mican be further restricted on the arcbased on the estimated ril.

Fig. 4 Missile position estimation.

Fig. 5 1st derived from Fig. 4.

Fig. 6 2nd derived from Fig. 4.

3.2. Two-stage cooperative guidance law for stationary target

Fig. 7 Relative position among the leader, follower and stationary target.

Remark 1. If the leader employs the PNG (proportional navigation guidance), its time-to-go satisfies18

where Δτ is a sufficiently small time interval.It means that the estimated impact time of the leader tlwould keep constant during the flight. Therefore, the follower is required to communicate with the leader only at the initial time, to derive the guidance information employed in Stage 1. Hereafter, the motion of the leader would have no impact on the guidance of the follower.

Remark 2. In Stage 1, the impact time constraint exerted actually aims to implementing the intensive attack.Due to the fact thatreaches T′at the moment tl-rT′T/viand flies straightly in Stage 2,can reach the target T at the same time with the leader theoretically. Therefore, the impact time error between the real position Miand the leader can be derived as

Fig. 8 Relative position among ， Mi and the target.

Fig. 9 Procedure for two-stage cooperative guidance law.

4. Extension to maneuvering target

For the maneuvering target, two new requirements on the cooperative guidance law are introduced based R2 and R3:

R3m:and Mlcan reach the target simultaneously.

4.1. Cooperative guidance law based on consensus theory

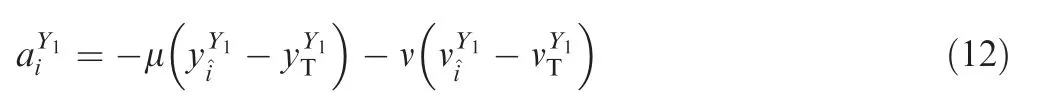
where μ and ν are both positive constants; and

In conclusion, the new guidance requirement R2mcan be satisfied by Eq. (12).

where k1is a positive constant.

Fig. 10 Positions of the leader, follower Mi and target in reference coordinate OX1Y1.

Therefore, the normal and tangential acceleration commands of the follower can be derived as

4.2. Cooperative guidance law based on finite-time convergence approach

During the cooperative guidance law derived in Section 4.1,the absolute positions of the target and estimated followerare employed,which requires extra estimation and calculation.Therefore,a more direct cooperative guidance law is proposed here,in which the relative motion states obtained by the direct measurement are employed. That is to say both the calculation burden of the acceleration command and the communication delay induced by these calculation can be reduced.

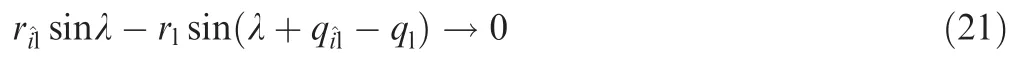
Moreover, according to Fig. 11 and Eq. (23), one has

Fig. 11 Relative position among the leader, follower and maneuvering target.

The tangential acceleration command of the follower can be derived to implement Eq. (23). Firstly, substituting Eq.(23) into Eq. (4) yields

Then, taking the derivative of Eq. (25), one has

Through simplifying Eq. (26), one can derive that

Moreover, to guarantee the equivalence between Eqs. (25)and (27), the initial state vi0is required to be satisfied as

Due to the faster convergence rate and higher convergence precision of the finite-time convergence theory,20the finitetime convergence of Eq. (21) can be implemented by

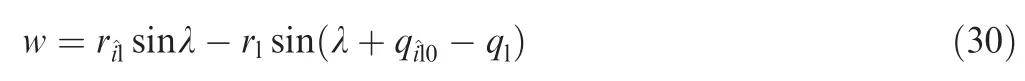
By taking the derivative of Eq. (30), ˙w can be expressed as

To prove that Eq. (29) can implement the finite-time convergence of Eq. (21), Lemma 1 is introduced as follows.

Lemma 1.21Consider the system ˙x=f x( )， x ∈Rn, with the condition f 0( )=0. f ·():Rn→Rnis a continuous function. If there exists a continuous positive definite function, which is defined within the neighborhood of origin as Z x( ):Rn→R and satisfies ˙Z x( ) + c Z x( )( )ξ≤0 (c ＞0 and ξ ∈ 0，1( )), then the origin of the system ˙x=f x( ) is finite-time stable and the settling time T satisfies T ≤［Z (x (0 ))］1-ξ/［c (1 -ξ)］.

The following proof procedure guarantees that Eq.(29)can implement the finite-time convergence of Eq. (21):

The continuous positive definite function Z is defined as

Taking the derivative of Eq. (32), it can be derived that

Substituting Eq. (29) into Eq. (33) yields

Considering the fact that

one has

Substituting Eq. (32) into inequality (36) yields

This completes the proof.

Then,the normal acceleration command of the follower can be derived. Taking the derivative of Eq. (29) yields

where

Substituting Eq. (27) into Eq. (38) yields

Defining

and then substituting Eq. (41) into Eq. (40), one has

Therefore, the normal acceleration command of the follower is derived as

Moreover, to guarantee the equivalence between Eqs. (29)and (43), the initial state θi0is required to be satisfied as the first stage is required to be predetermined(td2),so as to predict the initial position and velocity vector of the target for the second stage by the motion prediction method. In summary,the required vi0and θi0can be obtained by Eqs. (28) and(44),based on the predetermined θl0and derived initial motion states for the second stage.

where k3is a positive constant. Therefore, the guidance requirements on vi0and θi0for the second stage can be satisfied. The procedure for the cooperative guidance law based on the finite-time convergence approach is illustrated in Fig. 12.

Remark 4. There are three cooperative guidance laws proposed in this paper.The cooperative guidance law proposed in Section 3.2 can directly employ the existing guidance law with the impact angle and time constraints. However, it is only suitable for the stationary target and the point T′is required to be pre-specified. The other two cooperative guidance laws proposed in Section 4 are suitable for the maneuvering target.

To satisfy the requirements on vi0and θi0(Eqs. (28) and(44)), it is required to introduce the guidance laws for the leader and follower during the first guidance stage, which are implemented before the cooperative guidance.Thus,the cooperative guidance law(shown in Eqs.(27)and(43))is employed during the second guidance stage.Firstly,it is required to predetermine the suitable terminal positions ofand Mlduring the first stage,so as to estimateandrequired in Eqs.(28)and (44). As the slant angle of(φ) is derived at the initial time of the first stage and keeps fixed hereafter, the required λ can be obtained by Eq.(22).Secondly,a suitable flight time for Compared with the cooperative guidance laws proposed in Section 4.2,the one proposed in Section 4.1 has a much easier guidance process, which however cannot guarantee the finitetime coordination of missiles, and requires the absolute positions of the target and estimated follower.

5. Simulation and analysis

A seeker-less follower is guided by a missile with the seeker,to cooperatively attack a single stationary or maneuvering target.It is assumed that the speed of the maneuvering target is constant,with a weaving maneuver for evading.To verify that the intensive attack could be conducted, the impact time error between the leader and follower is required to be less than 2 s. Moreover, in order to implement the precise attack, the miss distance, tangential and normal acceleration commands of the missile are required to be less than 5 m, 600 m/s2and 100 m/s2, respectively. In simulation, another seeker-less missile (namely reference follower) with the PNG or modified PNG22is employed for comparison,so as to explore the effectiveness and advantage of the proposed cooperative guidance strategy. The initial motion state of the reference follower is identical to that of the follower, and the LOS rotation rate required in the acceleration command of the reference follower can be derived as15

5.1. Cooperative strategy for stationary target

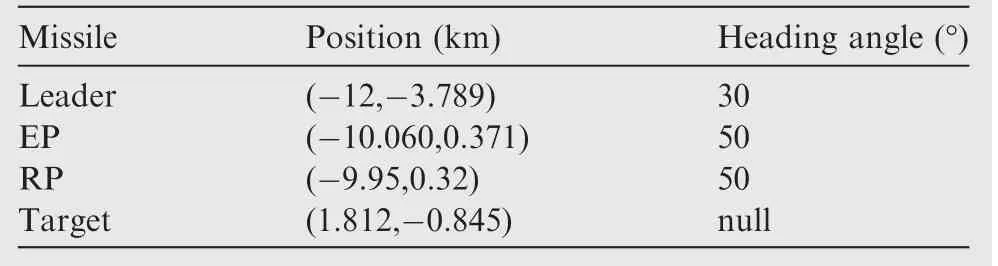
Table 1 Initial conditions of missiles and stationary target.

Fig. 13 Simulation results for stationary target.

Fig. 14 Impact of rT′T on guidance property.

Fig. 15 Impact of the localization error of on miss distance.

Fig. 16 Impact of ril0 on maximum miss distance.

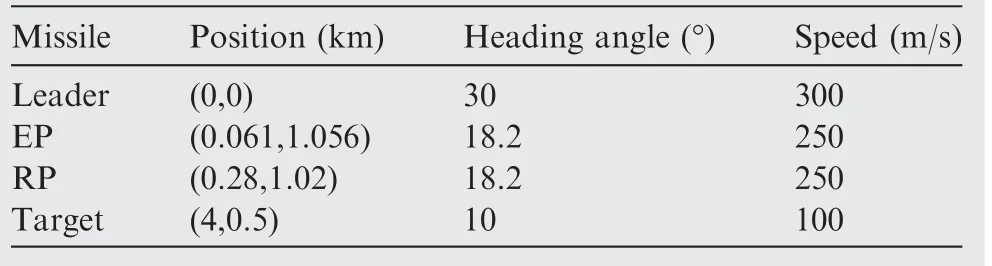
Table 2 Initial conditions of missiles and maneuvering target for guidance law based on consensus theory.

5.2. Cooperative guidance for maneuvering target

The simulation results are presented in Fig.17,in which RF denotes the reference follower.

Table 3 Simulation results for different localization error for guidance law based on consensus theory.

Fig. 17 Simulation results for cooperative guidance law based on consensus theory.

In Fig.17(a), the trajectories of the target and missiles are illustrated,from which it is found that the leader,the estimated follower and follower can all attack the target, while the reference follower cannot. Fig.17(b) shows the missile-target distance,in which the miss distances of RP and RF are 1.73 m and 150.36 m, respectively. Clearly, the follower satisfies the requirement on miss distance,while the reference follower does not, which verifies the effectiveness and advantage of the proposed cooperative guidance law based on the consensus theory. Moreover, the impact time difference between the leader and follower is merely 1.11 s, which guarantees the intensive attack of multi-missiles. Fig.17(c) and (d) indicate that both the normal and tangential accelerations of the follower can satisfy the constraint by employing the saturation function. In Fig.17(c), it shows that the normal acceleration command changes drastically in the first 5 seconds. The reason is that the parameters in the guidance law(i.e.μ，υ and k1)are deliberately chosen to be slightly greater, so as to reduce the miss distance of the follower.

Table 4 Initial conditions of missiles and maneuvering target for guidance law based on finite-time convergence approach.

Fig. 18 Simulation results for cooperative guidance law based on finite-time convergence approach.

Fig. 19 Simulation results without the influence of the guidance property of the first stage.

5.2.2.Cooperative guidance law based on finite-time convergence approach

The simulation results are presented in Fig. 18.

The trajectories of the target and missiles are illustrated in Fig.18(a). Fig.18(b) shows the missile-target distance, in which the miss distances of RP and RF are 1.1 m and 157.18 m, respectively. Clearly, the follower satisfies the requirement on miss distance,while the reference follower does not,which verifies the effectiveness and advantage of the cooperative guidance law based on the finite-time convergence approach. Moreover, the impact time difference between the leader and follower is merely 1.04 s, which can guarantee the intensive attack of multi-missiles. Fig.18(c) and (d) indicate that both the normal and tangential accelerations of the follower can satisfy the constraint by employing the saturation function. Fig.19(a) and (b) indicate that under the condition,i.e. the guidance requirements on the first guidance stage are satisfied,the LOS angle betweenand the leader keeps constant,and the square of the position error betweenand the point C (Z, defined in Section 4.2) can converge to 0 within finite-time, which means that the guidance requirements on the normal and tangential acceleration can be respectively implemented. Moreover, it can be derived that the differences between Figs. 18 and 19 are merely induced by the first guidance stage.

Table 5 Simulation results for different localization error for guidance law based on finite-time convergence approach.

Assume that the initial guidance requirements on the second stage can be completely satisfied. Then, the simulation results for different initial position of Mi,i.e.different localization error for, are shown in Table 5. It is noticed that the miss distances of the follower always satisfy the constraint,while the miss distances of the reference follower are far beyond the constraint.Therefore,it can be further verified that the cooperative guidance law based on the finite-time convergence approach can guarantee the precise attack of the follower with different localization errors.

6. Conclusions

To address the issue that the localization error of the seekerless missile induces greater miss distance, a new cooperative guidance strategy of multi-missiles is proposed in this work,with the assumption that the measurement error of the velocity for the seeker-less missile can be neglected during the terminal guidance.Within this proposed cooperative guidance strategy,the slant angle of the line between the estimated and real positions of the seeker-less missile is approximately derived through elaborately selecting the estimated position of the seeker-less missile firstly. Then, based on the derived slant angle, one and two cooperative guidance laws are respectively developed for a stationary and maneuvering target to implement the fire-and-forget attack of the seeker-less missile, with which the intensive attack can also be achieved to improve the capability of defense penetration. Simulation results demonstrate the effectiveness and advantages of the proposed cooperative guidance strategy.

Note that in practical application, the acceleration of the maneuvering target is generally difficult to be obtained accurately, of which the measurement error would influence the cooperative guidance performance of the proposed cooperative guidance laws,such as the increase of the miss distance of the follower and the augment of the impact time error of missiles. Therefore, this issue will be studied in the future.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (No. 11532002) and the Hongjian Innovation Foundation of China (No. BQ203-HYJJ-Q2018002).