Exploration and implementation of commonality valuation method in commercial aircraft family design

Yongjie ZHANG, Zheng YANG, Xinho MA, Wenjun DONG,Dyong DONG, Zhogung TAN, Shui ZHANG

a School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

b Shanghai Aircraft Design and Research Institute, Shanghai 200232, China

c Beijing Aeronautical Science & Technology Research Institute, Beijing 102211, China

KEYWORDS

Abstract Commercial aircraft family design can reduce development costs, shorten development cycles, and expand the market coverage of aircraft. Commercial aircraft family development has become one of the most important features of modern aircraft design. This paper explores the effects of commonality on different aircraft models in a commercial aircraft family. The existing product commonality indexes are summarized and their limitations in the application to aircraft design are discussed. Then a new component commonality index is proposed based on the component decomposition structure. A model for calculating the aircraft program value is established,which considers development costs, manufacturing costs, sale price, operation costs and residual costs. The effects of aircraft commonality on time and economic costs of both development and manufacturing, and on sale price, are analyzed and quantified. The commonality evaluation strategy is obtained,which features comprehensive consideration of the aircraft program value and time costs.The break-even analysis of aircraft is proceeded on the basis of costs and price data.By using a real option method, the strategy considers the uncertainty of the aircraft program and the flexibility of the manufacturer. This strategy proves to be rational and applicable to aircraft design based on the calculation of three examples and the analysis of parameter sensitivity.

1. Introduction

A product family, an advanced form of standardization, is a set of related products that share common attributes such as features, components, modules, or subsystems. Based on the relationship between products within a product family,designers can create reasonable plans about the main parameters, types and sizes of products, analyzing the development rule of similar products, predicting the market demand trend,and making technical/economical comparisons.1-9

The development of an aircraft family is an important characteristic of modern commercial aircraft design. The aircraft family usually consists of baseline aircraft and its derivatives or variants.10It is a common practice to derive fuselagelengthened or fuselage-shortened type from baseline aircraft so as to reduce Research and Development (R&D) costs,shorten R&D cycles, improve the adaptability of aircraft routes and airports, and expand the market coverage of aircraft products.11-14

Commonality,an important concept in the product family,refers to the reuse and sharing of assets (components, manufacturing processes, architectures, interfaces and infrastructure) across members in a product family, representing a potential strategy for improving the company’s profitability.15The challenge of designing a product family is to resolve the trade-off between commonality and distinctiveness: if commonality is too high, products will lack distinctiveness, and their individual performance will not be optimal; in contrast,if commonality is too low, manufacturing costs will increase.It is better to obtain commonality by minimizing the nonvalue added variations across the products within a family without limiting the choices of customers in each market segment; that is, each product within a product family should be distinct in ways that customers can notice, and identical in ways that customers cannot see.16

To help evaluating the trade-off mentioned above, many commonality indexes have been proposed. A commonality index is a metric that assesses the degree of commonality within a product family based on different parameters (e.g.,the number of common components, component costs, and manufacturing process).These indexes can be used to estimate the cost saving of products within a family, and are usually considered at the beginning of the design of a new product family or the analysis of an existing family. After analyzing and comparing with the existing commonality indexes, this study proposes a new metric, and establishes an model for evaluating commonality effects based on aircraft program values and time reduction.The effects of aircraft commonality on R&D time and economic costs, manufacturing time and economic costs, sale price, and pilot training time are then quantified.

2. Commonality index

This section briefly introduces the existing commonality indexes and their limitations in the implementation in commercial aircraft family design,and then presents a new commonality index applicable to commercial aircraft family design.

2.1. Overview

Table 1 lists the existing commonality indexes based on different parameters (number of identical components, connection method,costs,etc.).These indexes have all been used to guide the design or redesign of a product family.

2.1.1. Degree of commonality index

The Degree of Commonality Index (DCI)17is the most traditional measurement method for component standardization based on the average number of common parent items per average distinct component part:

where φjis the number of immediate parent components and j has over a set of end items or product structure level(s);d is the total number of distinct components in the set of end items or product structure level(s);i is the total number of end items or the total number of highest level parent items for product structure level(s).

The main advantage of the DCI lies in its easy calculation.However, it is difficult for the DCI to estimate the increase in commonality when a series of products are redesigned or different series of products are compared, because the DCI does not have a fixed boundary (with a range from 1 to ∑i+dj=i+1φj).

2.1.2. Total constant commonality index

The Total Constant Commonality Index (TCCI)18is a modified version of the DCI. Contrary to the DCI, the TCCI is a relative index with absolute boundaries ranging from 0 to 1:

The absolute boundaries of the TCCI facilitate comparisons of products between different families or within a same family during redesign.

2.1.3. Commonality index

The Commonality Index(CI)19,20is also a modified version of the DCI, which measures the unique parts in a product famility:

where u is the number of unique parts; pjis the number of the parts in the model j;vnis the final number of varieties offered.

The CI ranges from 0 to 1, and can be interpreted as the ratio between the number of unique components and the total number of the parts in the product family.

2.1.4. Percent commonality index

The Percent Commonality Index (%C)21is based on three main viewpoints: component viewpoint, viewpoint of component-component connections, and assembly viewpoint.Each viewpoint produces a percentage of commonality, and can be combined with other viewpoints to determine an overall measurement of commonality by weighting each percentage value. The component viewpoint measures the percentage of platform components that are common among different models, and the percent commonality of components, Cc, is given by

Table 1 Summary of product commonality indexes.

The component-component connection viewpoint measures the percentage of common connections between components,Cn:Similarly, the assembly viewpoint measures the percentage of common assembly sequences, using two indexes: Cl, which measures the percentage of common assembly sequences, and Ca, which measures the percentage of common assembly workstations:The four values mentioned above can then be combined into an overall platform commonality measure and the weighted-sum formulation is given by:

The resulting %C ranges from 0 to 100, takes manufacturing and assembly into consideration, and can be adapted to different strategies with weighting factors. The disadvantage of this index is that the measure can be applied to each platform but not to the whole product family.

2.1.5. Product line commonality index

Contrary to the indexes that simply measure the percentage of components that are common across a product family (and hence penalizing families with a broader feature mix),the Product line Commonality Index (PCI)22measures and penalizes the differences that should ideally be common, given the product mix. The PCI is given by

where P is the total number of non-differentiating components that can potentially be standardized across models; N is the number of products in the product family; niis the number of products in the product family with component i; f1iis the size and shape factor for component i;f2iis the factor of materials and manufacturing processes for component i; and f3iis the factor of assembly and fastening schemes for component i.

f1iis the ratio of the largest number of models that share component i with the identical size and shape to the largest possible number of models that could have shared component i with the identical size and shape (ni). The PCI has fixed boundaries that range from 0 to 100,focusing on the commonality that should exist between products with common or variant components rather than on the unique components. The PCI provides a single measure for the entire product family,but it does not offer insight into the commonality of the individual product within the family.

2.1.6. Component part commonality index

The Component Part Commonality Index, CI(C),23is an extended version of the DCI that considers product volume,quantity per operation,and the cost of component parts,given by

2.1.7. Common commonality metric

The Common Commonality Metric (CMC)24evaluates the design of a product family at a ratio of 0 to 1 based on the component, size, shape, material, manufacturing process,assembly, cost, and diversity allowed for each product in the product family. The CMC is given as follows:

where P is the total number of components;niis the number of products in the product family with component i; fxiis the ratio of the largest number of products that share component i with the identical factor (the factor is size and shape for x=1, materials for x=2, manufacturing processes for x=3,assembly and fastening schemes for x=4)to the number of products with component i(ni);fximaxis the ratio of the largest number of products that share component i with an identical factor(the factor is size and shape for x=1,materials for x=2, manufacturing processes for x=3, assembly and fastening schemes for x=4) to the largest possible number of products that could have shared component i with identical factor;Ciis the current total cost of component i;Ciminis the minimum total cost of component i (obtained when the component is common among all the products with component i);Cimaxis the maximum total component costs(obtained when the component is variant in each of the products with component i).

The CMC is comprehensive;however,it requires analysis of a large number of cost data which may not be available in the early stage of aircraft design.

2.1.8. Index analysis

There are some limitations or deficiencies in the existing commonality indexes when they are used in aircraft design.Table 2 shows the comparison of commonality indexes based on the considered information in each index. As shown in the table,the DCI and CI(C)do not have fixed boundaries; the DCI,TCCI,CI and%C do not take size,geometry and manufacturing process into consideration; the PCI fails to consider the information of component costs.

Although the PCI and CI(C)consider much information of components, they still suffer from many limitations. First, the assumption that all the factors considered in the index have the same weight is not comprehensive, because different factors may influence the index by varying degrees. Second, calculating these two indexes involves the quantity of each product.This means that the analysis of aircraft family design concerns all the products in the entire market, so neither of the two indexes can easily measure commonality of individual product models. In other words, considering the production quantity will complicate the determination of the index for aircraft commonality measurement, in addition to the uncertain sale volume of an aircraft model at the beginning of the analysis.The focus of this research is to compare the commonality implementation among different aircraft models within a family; therefore, the commonality index should be a definite parameter for a certain aircraft model rather than a parameter changing with the production quantity.

The CMC captures comprehensive information for each component by integrating various aspects of different indices into a single measurement formula, it also considers penalty of the non-differentiating components by using the parameter fximax.As introduced in the Ref.24,the author used the CMC to carry out calculations for the product family redesign of a stapler family. The calculations involved a lot of data and information even though the stapler only consists of a dozen parts. However, the collection of information and the estimation of data for an aircraft analysis would be too complex. As a result, using the CMC to calculate the commonality degree of the aircraft suffers an insufficient feasibility.

2.2.New commonality index based on component decomposition

Based on the existing commonality indexes,we propose a new commonality index for aircraft design based on component decomposition levels.Compared with the indexes listed above,the index we create is more suitable for the analysis of aircraft family design that considers sufficient factors related to aircraft and ensures the simplicity of data collection and calculation.

The component commonality index proposed mainly evaluates the extent of commonality of aircraft components and the entire aircraft within the aircraft family. It is used for the analysis in R&D and manufacturing process.Before proposing the component commonality index, this study introduces two types of aircraft component decomposition structures. It is necessary to define a decomposition structure that the index analysis can follow because the index should be able to measure the commonality of parts and components in different levels.

2.2.1. Component decomposition structure

Table 2 Comparison of commonality indexes based on considered information.

To analyze component commonality factors, three levels of aircraft component decomposition, including the product,component, and sub-component levels, correspond to the calculation and analysis accuracy. For example, when obtaining the commonality index,the index value of the commercial aircraft system can be gained directly at the system level;or it can be obtained at the element level corresponding to the system,and the index values of different elements can be weighted and summed up. Although the planning of the commonality concept can start from a top-down perspective, the implementation of the commonality concept and the calculation of the commonality index should follow a bottom-up approach.

There are two types of commonly-used structural decomposition of aircraft components: Product Breakdown Structure(PBS) and aircraft manufacturing specification published by Air Transport association of America (ATA). The selection of the structural decomposition is decided by the requirements for computing the commonality of commercial aircraft components.Note that the PBS and ATA are merely two examples of the decomposition structure, the aircraft designers could also use different frameworks to calculate the commonality index if the manufacturer could offer sufficient data.

PBS reflects the various components of the product through a tree structure, with each type of components appearing only once in the structure. PBS has been widely used to develop products and components. The first three levels of the aircraft PBS are shown in Table 3.

Table 3 PBS decomposition.

ATA refers specifically to a classification structure given in the ATA100 specification, which rationally divides aircraft manufacturing and routine maintenance into different chapters. The ATA100 specification and technical data adopt the‘‘system-subsystem-single item” numbering method. The first three levels of the ATA structure are shown in Table 4.

2.2.2. Aircraft component commonality index

This section presents the formulation of the aircraft component commonality index which considers the influences of factors such as component costs, size and shape, material selection, manufacturing process, assembly and fastening scheme. The calculation target can be a component (at Level-2), a sub-component (at Level-3), or a part level (at Level-4,which is not shown in Table 3 or Table 4).All components,sub-components and parts are referred to as the module in this paper. The module can be divided into the homemade module and outsourced module. The commonality index for the homemade module is given as

where CIiis the commonality index of module;Ciis the cost of module i,for homemade module it is the material and processing cost of the mudule i,together with the average set-up cost;ω1，i, ω2，i, ω3，i, and ω4，iare the weight factors of the size and shape,material,manufacturing process,and assembly and fastening scheme of module I,respectively;f1,i,f2,i,f3,iand f4,iare the factors of size and shape,material,manufacturing process,and assembly and fastening scheme of module i, respectively.

ωx，iranges from 0 to 1, and ω1，i+ω2，i+ω3，i+ω4，i=1.Each weight factor is to be defined by professional designers according to the actual R&D and manufacturing process of each module. f1,imeans the commonality relationship of the size and shape of module i between the target aircraft and the baseline aircraft. If the size and shape of module i are the same for these two aircraft models, the value of f1,iis 1;if different, the value is 0. The meaning of other fx,iis similar to that of f1,i.

For the outsourced module, the factor of manufacturing process can be neglected, so the corresponding commonality index is given as

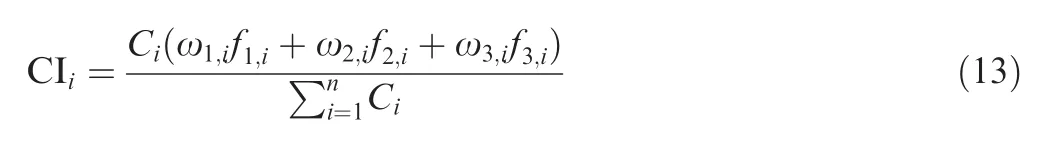
where Ciis simply the purchasing cost of the module i.

Table 4 ATA decomposition.

3. Model for calculating aircraft program value

This section introduces a model for calculating the aircraft program value, the basis of subsequent commonality effect evaluation. The overall framework and modules of this model are introduced in detail.

3.1. Framework of model

Aircraft design is regarded as a general engineering issue,with different objective functions for each stakeholder in the program.For example,aerodynamic experts regard the maximum lift-drag ratio as the objective function; load engineers believe that the maximum payload capacity (or passenger seats) is of great importance; and for commercial aircraft production companies which participate in the global market competition,the objective function is the maximum benefits of aircraft programs, since profitability is their primary purpose.

We study the benefits of commonality for the aircraft family design from the perspective of aircraft manufacturers, and thus select the aircraft program value as the objective function to model the entire aircraft design issue.The program value is defined as the maximum production profit that a program brings to aircraft manufacturers. The structural overview of the model is shown in Fig. 1.

3.2. Module introduction

Fig. 1 Structural overview of the calculation model of aircraft program value.

The calculation model for the aircraft program value is created under the framework of the Aircraft Life Cycle Cost(ALCC).According to ALCC, no matter how many airplanes are ultimately produced, research, development, test and evaluation costs will remain basically unchanged and non-repetitive.Therefore,R&D costs are also called non-recurring cost.However, unlike R&D costs, manufacturing costs are recurring,meaning that the costs will be incurred repeatedly for each plane. The more airplanes produced, the lower manufacturing costs per unit.

The calculation model designed is divided into four modules: R&D costs, manufacturing costs, sale price and sale quantity, which are introduced as follows.

3.2.1. R&D costs

The development of a new commercial aircraft typically lasts for about 5 years. R&D costs can be divided into five categories: engineering; manufacturing engineering (materials and equipment);tool design;tool fabrication;and support(quality inspection and testing). Note that R&D costs will be spent only once during the aircraft program, so they are nonrecurring.

Based on the data from Ref. 25, the R&D costs per pound of each component is shown in Table 5.Since the information obtained from the public literature is very limited, the data in Table 5 are only used as reference in the preliminary calculation of the commonality valuation model. Note that researchers can use other component classification and cost data if more authoritative information could be obtained.

The R&D costs of the whole aircraft are given as:

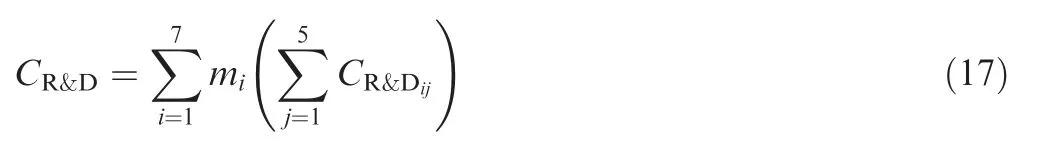
where CR&Dstands for the R&D costs of the whole aircraft;miis the weight of component i; CR&Dijis the R&D costs per pound of component i and process j.

3.2.2. Manufacturing costs

Manufacturing costs are subject to a learning curve effect. As workers become more skillful in the process of production,the unit manufacturing costs can gradually decrease,eventually to a negligible level when the unit costs remains roughly constant.The learning curve effect is quantified as

where MC is the marginal unit cost;TFU is the theoretical first unit cost; Q is the quantity built to date; s is the slope coefficient of the learning curve. The implication of this formula is that when the number of the units doubles, the production time (or cost) is reduced by s percent of its original value.

Based on the typical value of s given in Ref.26,0.9 is taken for manufacturing, 0.75 for assembly and 0.98 for material.Fig. 2 shows the effects of the learning curves.

The manufacturing costs per pound of each component is shown in Table 6.Note that‘‘Final assembly”in the manufacturing cost breakdown does not appear in the R&D cost model. It is not technically a component of aircraft, but is assigned with a value of distinct cost per pound. Its corresponding weight in calculation is the aircraft’s empty weight.

The manufacturing costs of the nth aircraft are given as

where Cmnrepresents the manufacturing costs of the nth aircraft;TFUjis the manufacturing costs of process j for the first unit;sjis the learning curve factor of process j;is the weight of component i; TFUijis the manufacturing cost of component i and process j for the first unit.

3.2.3. Operating cost

The Total Operating Cost (TOC) of aircraft can be divided into two categories: the Direct Operating Cost (DOC) and the Indirect Operating Cost(IOC).The DOC27is an important index to determine the economy of aircraft operation, which accounts for more than 50% of the TOC. The DOC can be regarded as a technical criterion for comprehensive assessment of the aircraft’s market environment, overall parameters,maintenance requirements and flight performance. Therefore,the research on aircraft operating cost mainly focuses on the analysis of the DOC.

Fig. 2 Typical learning curves for different factors.

Table 5 R&D costs per pound of each component.

Table 6 Manufacturing cost per pound for each component.

In the composition of the DOC, the cost of cash is the biggest cost item for airlines. Its full name is the Cash Airplane-Related Operating Cost (CAROC), and its unit is$/ASM (dollar per available seat n mile). In order to take the operating cost into the consideration of the aircraft pricing process,the CAROC is divided into the nominal CAROC and the actual CAROC.

The Ref. 25 analyzed the linear regression of the CAROC data of some narrow-body and wide-body aircrafts.The fitting equations are as follows:

where CAROCnominalis the CAROC of an aircraft in the normal condition, the value of it is based on the seat count of the aircraft.

In addition,the actual CAROC is the estimation of the cash cost of an aircraft in actual operation based on certain assumptions.The wages paid by airlines to pilots and crews are different,the equipment maintenance also varies with companies,so the fuel cost is the most easily quantifiable and stable cost item(the fuel cost generally account for about 20% of CAROC).Therefore, the actual CAROC can be derived by calculating the fuel cost.

The Ref. 25 calculated the fuel burn and fuel cost of some aircrafts, and the fitting equation of the ratio parameter ‘‘fuel cost/CAROC” is as follows:

After obtaining the fuel cost ratio of an aircraft, its actual CAROC can be calculated using the equation:

where CAROCactualis the actual CAROC of the aircraft;Wfuelis the fuel burn for the reference range mission;Pfuelis the fuel cost.

3.2.4. Sale price

The price of aircraft is modeled as a function of several variables.By adjusting the function parameters,the mean squared error of estimated price is minimized.The following formula is the price definition function, which shows that the price has a nonlinear relationship with seats and a linear relationship with range.

where Price refers to airplane price with multiple variables;△(LC) is the increment of lifecycle costs due to the CAROC,which will be explained in the next paragragh;Seats and Range are the seat count and design range (nm) of the aircraft;Seatsref, Rangeref, and Pricerefare reference values that normalize the number of seats, range, and price, respectively; k1,k2and α are model parameters selected to minimize the mean squared error of estimated price.

The increment of lifecycle costs,△(LC),is explained as follows: if the CAROC of the aircraft is higher (or lower) than expected due to the implementation of a series of design concepts or due to design deficiencies,the airline and other buyers would believe that they could get an extra loss (or benefit).This loss(or benefit) can be quantified as the expected present value of additional expenses (or savings) from operating the aircraft over its lifetime. When the buyer and seller negotiate the price, the buyer would want to give the manufacturer less money,or the manufacturer hopes to share this part of benefit,i.e., △(LC).

As discussed in the Section 3.2.3, the changes in CAROC are also divided into two types: the changes related to the fuel cost and the changes related to the other costs,including maintenance, crew and ground costs. Correspondingly, △(LC) is also divided into two parts: the part related to the fuel cost in CAROC and the part related to the non-fuel cost in CAROC. The equations of △(LC) are given as:

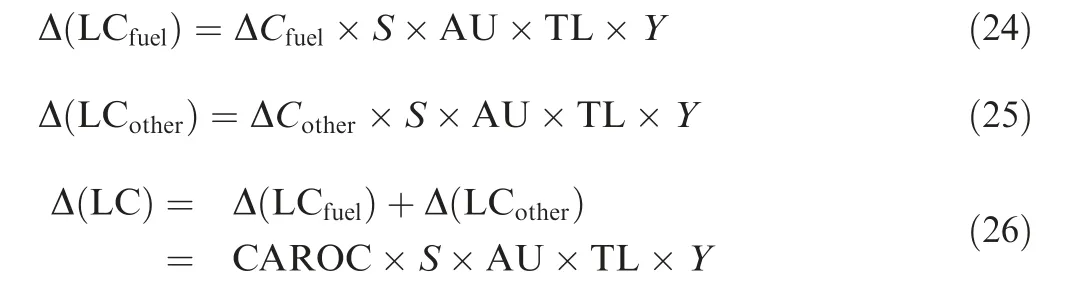
The △(CAROC) is defined as:

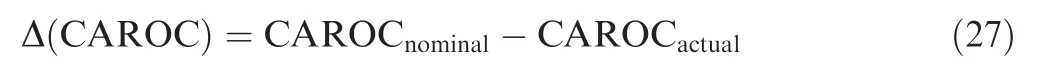
The △(LC) is the discounted value of the △(CAROC)within the service years. The specific calculation of Eq. (26)is given as follows:

where i is the number of the year; r is the operator discount rate.

The default values of some parameters used in the aircraft price calculation are shown in Table 7.

3.2.5. Program value calculation based on real option method The shareholder value of the aircraft manufacturer is selected as the ultimate objective function of the aircraft design problem in this study. The aircraft value should be defined as the maximum profit that the entire aircraft program brings to the aircraft manufacturer, and the goal pursued by the company should be the maximization of the total profit of the aircraft program.Therefore,the shareholder value of the aircraft manufacturer can also be called the aircraft program value,and it is defined as:

Table 7 Default values of parameters for aircraft price calculation.

where value is the aircraft program value (the sum of the net profits of all N aircrafts produced); Price is the selling price for each aircraft; Cmis the manufacturing costs of all N aircrafts.

The most commonly used method for calculating the program value is the Net Present Value (NPV) method, but the traditional NPV method does not consider the uncertainty of the aircraft design program nor the flexibility of the aircraft manufacturer. Uncertainty is also known as risks, including technical and market risks. The former can be resolved within the company,while the latter mainly reflects the fluctuation of aircraft demand. Flexibility includes various investment decisions of manufacturers.

Therefore, this study uses the real option theory as the calculation and decision tool to evaluate the program. This theory involves many mathematic models. Among the most commonly used models, the binary tree model is selected to calculate the aircraft program value,and the specific operation is shown in Fig. 3.

Fig. 3 Binary tree model for calculating aircraft program value.

The model in Fig.3 is explained as follows.First,according to market forecasts, the aircraft’s baseline demand quantity is obtained and used as the starting point data.Then,in order to take uncertainty into consideration, we use the binary tree model to quantify the aircraft annual demand. The market of commercial aircraft is affected by many unpredictable fluctuations at demand levels. These fluctuations, represented by aircraft orders (which will become deliveries), are caused by various factors such as fuel price, public willingness to travel,airline profitability, gross domestic products, interest rates,and global economic conditions. All these factors show more or less random fluctuation behaviors. Ref. 12 points out that two kinds of parameters need to be calculated to simulate the dynamics of sale quantity: growth rate and volatility.The average growth rate is obtained from the total delivery of narrow-body and wide-body aircraft; the volatility is considered as the average of individual aircraft volatilities,weighted by the number of deliveries of each airplane.

Assuming that the baseline market demand quantity is N.After a period of time Δt(here is 1 year),the demand quantity may rise to uN by probability p, or decrease to dN by probability 1-p.The parameters mentioned in this sentence are calculated as

where u is the increase rate of aircraft annual demand;d is the decrease rate of aircraft annual demand; σ is the volatility of aircraft annual demand; Δt is the unit time step; rfis the risk-free rate.

To simulate the flexibility of the decision-maker, the aircraft manufacturer can choose to invest or abandon investment at the end of the program decision period Td (here T=2), or choose to invest or defer investment at each time node (T=0, 1) within Td.

The demand at Td will have multiple possible values (here are u2N, udN, and d2N). The corresponding aircraft program values (S0u2,S0ud, and S0d2) are calculated, and then the program value at the previous moment is reversely calculated to determine whether it is worthwhile to continue investing at each time node. The program value at T=0 is finally calculated.

The formula for calculating the aircraft program value at the time of Td is given as

The formula for calculating the aircraft program value reversely at the previous moment T-1 is:

After calculating the program value reversely to the starting point T=0 by following the above formula,we finally obtain the value of the aircraft program based on the real option method that considers uncertainty and flexibility.

4. Impact of commonality on aircraft program value

This section presents a quantitative analysis of the impact of commonality of airplanes at various stages of an aircraft family design, and considers the commonality effects on the modules of the calculation model for the aircraft program value introduced previously to obtain a complete evaluation model of commonality impact.

4.1. R&D costs

Since the tools corresponding to the common components already exist (unless new tools are needed), the cost savings mainly occur in tool design and tool fabrication. For the rest processes, such as manufacturing and support, the cost and time can also be partly saved because of the previous equipment and personnel experience from the last aircraft model.

Based on the reasonable first-order estimation, the R&D cost reduction factors are shown in Table 8.The reduction factors indicate the cost saving proportion when two aircraft models have one completely identical component,in such case the value of the commonality index is 1.

Therefore, considering commonality, formula (17) is amended as

4.2. Manufacturing costs

Although the manufacturing costs for each aircraft are unavoidable, the commonality can have a great impact on the learning curve.Because workers can operate more skillfully with experience from the previous aircraft model, the learning curve can decease more quickly (i.e., the slope coefficient increases), which reduces material waste and saves manufacturing costs in turn.

The impact of commonality on manufacturing costs can be summarized as two main parts. First, due to the existence of some production equipment, tools utilizing the production equipment,and tools of the previous aircraft model,TFU will receive certain benefits from commonality, but the related costs of new equipment and tools are uncertain. Therefore, it cannot be concluded that the TFU will be reduced due to commonality.The viewpoint that the TFU will be affected by commonality is then proposed, and the specific value of the TFU will be determined by actual analysis.

Next, subjective factors such as the operators’ skill and technical improvement cannot be quantified easily, but corresponding data can be obtained through statistics. The commonality makes the learning curve factor reduce from s of the previous aircraft model to s′, formula (19) is amended as

where γijis the learning curve reduction factor of component i in process j;sjis the learning curve factor of process j,it is different for various processes,ranging from 0 to 1,but according to the NASA Cost Estimate Handbook,the general values are between 0.75 and 0.95.The estimation values for both sjand γijare to be obtained by accumulation within a certain period of time.

4.3. Sale price

For airlines, commonality implementation can reduce aircraft maintenance costs. The same components can use the same repair tools,spare parts are sufficient,and workers do not need additional training. For example, the cockpits with high commonality can increase fleet flexibility, and also reduce the time and cost of pilot training by reducing the number of flight simulators and ground instructors. Therefore, the operating costs can be significantly saved due to commonality. In the aspects of aircraft maintenance and personnel training, the time and cost savings of commonality implementation will come from many software aspects, such as logic, operational processes,interfaces and so on.Although the commonality index is more related to the hardware aspects of the component, it can also be used to analyze the operation of the aircraft. Because the software commonality is actually reflected by the hardware commonality, for example the same tools and processes can be used for maintenance as a result of the same linking method between parts.But the results can be more accurate if the commonality index takes the software aspects into consideration by obtaining enough information and data support.

Table 8 R&D cost reduction factors.

The residual value of commercial aircraft is the most important indicator of measuring the real-time value of aircraft. After entering the secondary market, the residual value of the aircraft becomes the focus of buyers and sellers. Due to the aircraft family development,the characteristics of systems,products and flights among different aircraft models have high commonality and high market share; thus, the residual value of the aircraft can be increased and the aircraft can have a wider usage space even after reaching the operating age. The retired aircraft can be converted to a cargo aircraft and sold to a shipping company, or it can be dismantled so that the common components or parts can be used for other aircraft models within the family.

All the above reasons can be used as selling points of aircraft. During the process of negotiating prices between manufacturers and airlines,the benefits can be used as an advantage to increase price. However, the pricing of aircraft is not only affected by commonality,for example the use of new technologies can also become an advantage to increase the price.Therefore, some scale factors are proposed here to quantify the impact of cost factors on aircraft pricing and the price can be predicted by adjusting the parameter values. Considering all the factors discussed above, the pricing formula of aircraft can be given as:

where β1is the scale factor of the impact of Δ( L Cfuel) on aircraft pricing; β2is the scale factor of the impact of Δ(L Cother)on aircraft pricing;β3is the scale factor of the residual value change in aircraft pricing; Crvis the aircraft residual value.

4.4. Time

4.4.1. R&D time Due to the tools, equipment and personnel experience of the previous aircraft model, resources can be utilized when a new aircraft model is developed.Therefore,in addition to considerable saving on costs, R&D time can also be saved significantly due to commonality.

Different processes in the R&D of aircraft have different starting time and total durations,so estimating the commonality of time saving for the R&D of the entire aircraft program needs to weigh many factors, such as determining if time saving will occur in the early,middle or late stage of each process,and considering the interaction between the time saving of different processes. Therefore, the entire program time saving is not definitive data.

Similar to R&D cost saving calculation, R&D time saving considers the time reduction factors and commonality index,based on the R&D benchmark time. The reduction factor is the ratio of the new R&D time to the original R&D time when the target aircraft uses exactly the same components as the baseline aircraft. It is currently assumed that the values of the R&D cost reduction factor in Table 7 are used in time reduction calculation.

The calculation formula for R&D time saving of the target aircraft is given as

where TSR&Djis the R&D time saving for process j; αjis the time reduction factor for process j; CIjis the commonality index for process j;TR&Djis the R&D benchmark time for process j.

4.4.2. Manufacturing time

Aircraft manufacturing can generally be divided into two categories: component manufacturing and assembly (including component assembly and final assembly). However, certain parts of the aircraft such as engines, instruments, airborne equipments, hydraulic system and accessories are manufactured by specialized factories, and are therefore not included in the scope of aircraft manufacturing. The final assembly work includes the installation of all parts as a finished product,the coupling of the entire system, and the laying of cables and conduits.

Fig. 4 shows the traditional working hour quota composition of aircraft manufacturing. Component manufacturing time and assembly time can be subdivided according to this figure.

Working time is the most important and meaningful part for the program. Commonality mainly affects the working time by the improvement of workers’ skill, production management techniques, continuous supply of materials, and timely information feedback. Therefore, when calculating the commonality of the manufacturing time saving, we only consider the working time. Calculation formulas are given as

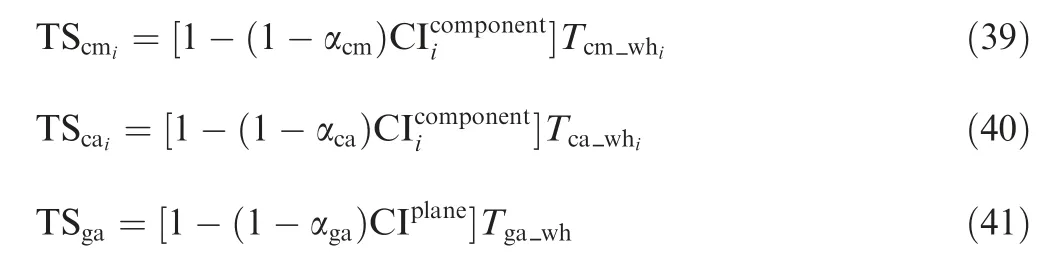
4.5. Commonality evaluation strategy

The above sections analyze and quantify the impact of commonality implementation on R&D cost and time,manufacturing costs and time,sale price under the ALCC framework,and obtain the time saving formula as well as the calculation formula for the aircraft program value considering commonality impacts. Table 9 summarizes the commonality parameters involved in each module of the model.

In applications,the commonality implementations of all the components of the target aircraft are counted, and the commonality indexes of all components and the entire aircraft are calculated.Then the index data are input into the program value and time saving formula, obtaining the results with the commonality implementation. This study also uses the default data to calculate the target airplane program value without the commonality implementation. Finally, based on the comparison between the aircraft program values in both cases (with and without the implementation of commonality), the value of the commonality implementation on aircraft family design can be obtained.

The basic data required for this commonality evaluation strategy (such as aircraft weight, range and other design parameters) is relatively easy to obtain, so with more accurate cost and other economic parameters, the results can be calculated efficiently. Based on the commonality evaluation strategy, it is possible to compare the effects of the commonality index of different components on the aircraft value and time saving, thereby providing suggestion and guidance for the design of the target aircraft.

4.6. Development of computing application

The calculations are achieved through an application developed in Visual Studio 2017 according to the aircraft program value calculation model. The programming language is C#.The main interface of the application consists of a title bar,a menu bar and four tabpages. The application mainly includes four modules: baseline aircraft data input module,commonality index analysis module, target aircraft data input module, calculation and result viewing module. The operation of data input and calculation between the four modules should follow the sequence.The application has concise interfaces and is easy to operate.

5. Examples

This section presents three numerical examples of aircraft design with relevant input data. The results are calculated out by the computing application.

5.1. Example of A320 and A319

Airbus single-aisle aircraft includes four types: A318, A319,A320 and A321, of which A318, A319 and A321 are designed on the basis of A320. These types achieve different passenger capacities by lengthening or shortening the airframe,and have the same cockpit and operating procedures that can reduce pilot training costs and maintenance costs and can increase operational flexibility.

Table 9 Summary of parameters of commonality.

The A319 model is a shortened version of the A320 model.The A319 removes one emergency exit on the wing and the bulk cargo compartment at the rear of the fuselage. However,the nose,the middle and rear sections of the fuselage,the wing,and the empennage structure of the A319 are all identical to those of the A320. In order to adapt to the reduction of the seats,the A319 fuselage has a shorter frame distance compared to the A320 fuselage. The pictures and geometry data of the two aircraft models are shown in Fig. 5.

Fig. 4 Work hour quota composition of aircraft manufacturing.

Fig. 5 Pictures and geometry data of A320/A319.

Table 10 Features of A320/A319.

This example takes A320 as the baseline aircraft and A319 as the target aircraft. The weight breakdown and some other features of the two aircraft models are listed in Table 10.The following data come from A320-200 and A319-100. The weight breakdown uses the weight fraction in Ref. 12 as an assumption.

The data of each component are unavailable,so we assume the values of the commonality index on the basis of the descriptive information in Table 10. The values are shown in Table 11.

Default data are employed for the R&D costs per pound,manufacturing costs per pound, and R&D cost reduction factors.The parameters used in the calculation are summarized in Table 12. As can be seen in Table 12, we examine the A319 model both with the impact of commonality, and without commonality implementation by assuming the values of all component commonality indexes are 0. That is, to evaluate commonality more concretely, we calculate and compare the program values of the target aircraft model in two conditions.

At first, the cost and price data are used to calculate the break-even of the aircraft program without considering the uncertainty and flexibility of the program. The calculation results are shown in Fig.6.It can be seen that when the target aircraft adopts the commonality strategy, the cost can be reduced and the program revenue can be increased,as a result,the aircraft break-even point will be moved forward from 452 to 199.

Fig. 7 shows the results of the commonality analysis of A319 in the form of binary tree model. The top line lists the time period from 0 to Tt; the binary tree shows the possible values of aircraft quantity (in black) and program value (in grey)in a given year;the last column shows the sum of aircraft quantity in the entire program.

Table 13 summarizes the results of the price and program value of A319. The unit of the results has been converted to CNY automatically in the application. Note that due to the saving of cost and the increase of price, the commonality implementation in the A319 model can considerably increase the program value (74.90%).

5.2. Example of B737-700 and B737-800

The new generation of Boeing 737 includes four models:B737-600/700/800/900. These four models have 98% commonality of mechanical parts, 95%-100% commonality of ground support equipment, and 100% engine commonality, resulting in satisfactory operating costs for airlines. The new generation 737 and the conventional Boeing 737 have almost the same cockpit so the crew’s driving qualifications are identical.Commonality also exists in spare parts,ground support equipment,and ground operations between the new and conventional Boeing 737 models, saving enormous costs for airlines.

The B737-800, a lengthened version of the B737-700, is designed with advanced technology, increasing fuel load and improving the operation efficiency.The cockpit dashboard features a new large-scale display screen. The example configurations are shown in Fig. 8.

This example takes B737-700 as the baseline aircraft and B737-800 as the target aircraft. The weight breakdown and some other features of the two aircraft models are listed in Table 14.

The data of each component are unavailable,so we assume the values of the commonality index on the basis of the descriptive information above.The values are shown in Table 15.

Default data are utilized for the R&D costs per pound,manufacturing costs per pound and R&D cost reduction factors. The summary of the parameters used in the calculation is presented in Table 16.

The results of break-even analysis of B737-800 are shown in Fig. 9. The aircraft break-even point will be moved forward from 53 to 17 when the target aircraft adopts the commonality strategy.

Table 17 summarizes the price and program value of B737-800. The commonality implementation in the B737-800 model can increase the program value by 35.46% and the sale price by 8.11%.Note that the pricing Eq.(32)is only an estimation and cannot take all the factors into consideration to model the real negotiation process.

5.3. Example of BWB 250-C and BWB 450

This example examines Blended-Wing-Body (BWB) aircraft.The BWB-450 model is a 450-passenger class aircraft and BWB-250C is a 250-passenger class aircraft. The latter is assumed to share a number of components with the former.Unlike conventional airplanes, the BWB airplane stretches in the spanwise direction and its passenger capacity can be increased simply by adding a central bay. Consequently, the BWB concept is found to be ideal for family development with a high potential for commonality realization.

Table 11 Commonality index of components of A319.

Table 12 Key inputs of A320/A319.

The fuselage bays are divided into cockpit, fuselage bay 1,fuselage bay 2, fuselage bay 3 and fuselage bay 4; the wings are divided into inner wing,outer wing and winglets.Assuming that BWB-250C has the same fuselage bay 2, fuselage bay 3,inner wing, outer wing and winglets as BWB-450 does, while the other components are completely different between the two aircraft models. The example configurations are shown in Fig. 10.

This example takes BWB-450 as the baseline aircraft and BWB-250C as the target aircraft. The weight breakdown and some other features of the two aircraft models are listed in Table 18.25

The commonality index of the wing is 1,because the two aircrafts use the same wings.To obtain the commonality index of the fuselage, we analyze the commonality implementation in the fuselage. Ref. 12 points out that in BWB-450, the cockpit is counted as part of fuselage bay 1 and fuselage bay 2,while it is regarded as an individual part in BWB-250C. To simplify the calculation, we assume that the cockpit in BWB-250C is completely different from that of BWB-450.Further,given the unknown cost information of each component,we assume that the unit cost of each fuselage bay is identical,so the cost percentage of each component becomes the weight percentage,and the final commonality index of the fuselage is 0.85.Table 19 shows the commonality index of each component in BWB-250C.

Similar to the example of B737-700 and B737-800, the example of BWB-250C uses the default data mentioned in Table 19 for the R&D costs per pound, manufacturing costs per pound, and R&D cost reduction factors. The summary of the parameters used in the calculation is listed in Table 20.

The results of break-even analysis of BWB-250C are shown in Fig. 11. The aircraft break-even point will be moved forward from 343 to 214 when the target aircraft adopts the commonality strategy.

The price and program value of BWB-250C are shown in Table 21. The commonality implementation in the BWB-250C model increases the sale price and program value by 6.75% and 36.57%, respectively.

The three examples given above show that the commonality evaluation strategy proposed here proves to be effective for both the conventional airplane and BWB airplane.The economic benefits of commonality,such as the increase of the program value,can be calculated and used as a trade-off factor for future research.

5.4. Sensitivity analysis

This section presents the effects of some varying parameters of the aircraft program value model based on the investigation of the BWB aircraft. First, model sensitivity to the component commonality index is addressed by comparing the calculations with different fuselage commonality indexes. Next, the effects of the parameters in the pricing model are discussed,including CAROC, β2and β3. Finally, the effects of decision duration and volatility are demonstrated.

5.4.1. Commonality index

Since the data of components are not ample enough,we could only confirm the commonality index of the wings of BWB-450 and BWB-250C as 1,assuming that the index of the fuselage is 0.85 based on the weight breakdown.Fig.8 shows the aircraft program value with different commonality indexes of the fuselage, ranging from 0 to 1. As can be seen in Fig. 12, there is a positive correlation between the value and commonality index,due to the cost saving from commonality implementation.

Fig. 6 Break-even analysis of A319.

Fig. 7 Binary tree of aircraft quantity and program value.

Table 13 Key outputs of A319.

Fig. 8 Pictures of B737-700 and B737-800.

Table 14 Features of B737-700 and B737-800.

5.4.2. △(CAROc)

△(CAROC) is heavily influenced by the fuel cost in the Eq.(24). The existing data and empirical function show that the value of △(CAROC)is usually close to or lower than 0.1;thus,we calculate the program value and sale price of BWB250-C with different values of △(CAROC), ranging from 0.02 to 0.11.As shown in Fig.13,the value remarkably decreases with the increase of △(CAROC), due to the fact that higher△(CAROC) means the airliner has to spend more operation cost than the average cost of the similar aircraft in the market.Therefore,the manufacturing company would be at an inferior position while the pricing and price of the aircraft decrease obviously.

5.4.3. β2and β3

β2and β3play important roles in determining the aircraft price,and their values will be negotiated by buyers and manufacturers. As shown in Fig. 9, there is a linear correlativity between the program value and β2or β3,since they are the primary term coefficients in the aircraft pricing formula.The program value increases with the decline of β2or the rise of β3.A lower value of β2means that the manufacturer has more advantages at pricing, because the aircraft will bring less non-fuel operation costs by using the commonality strategy or other advanced technology.A higher value of β3means that the aircraft has more residual value due to the family design and that this selling point is beneficial for raising the aircraft price. Furthermore, the impact of β2is greater than that of β3, as shown in Fig. 14.

Table 15 Commonality index of components of B737-800.

Table 16 Key inputs of B737-700/B737-800.

Fig. 9 Break-even analysis of B737-800.

5.4.4. Parameters in binary tree model

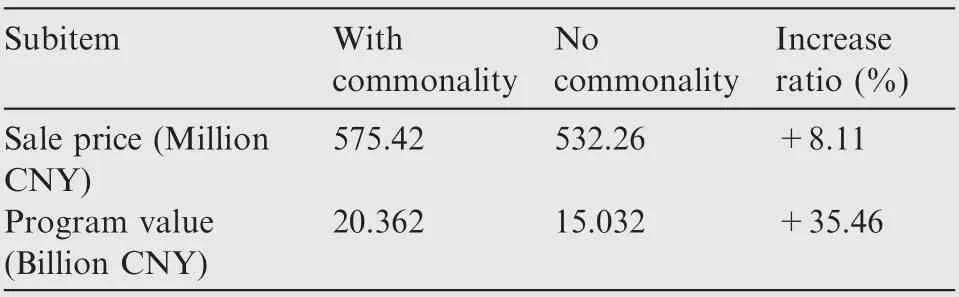
Table 17 Key outputs of B737-800.

Fig. 10 BWB example configurations.

Among the parameters in the binary tree model, three are examined in this study: Td, volatility and the risk-free rate.Fig. 15 shows the relationship between the program value and decision period. The value decreases with the increase of the decision period, which is consistent with the theory in the real option method. Since the total program time (30 years)is constant,the longer the manufacturer waits at the beginning of the program, the less time left for producing aircraft. The benefit of the entire program will also be reduced. Note that there is data fluctuation around Td=1 because the annual aircraft quantity is converted from decimal to integer when calculated in the program, thus causing a model error.

Table 18 Features of BWB-450/BWB-250C.25

Table 22 shows the effects of volatility and the risk-free rate. Both the two parameters are in direct proportion to the program value, and the impact of the risk-free rate is more obvious.A higher volatility means more risks of the program,which increases the choice space of management flexibility.Thus, the option of larger choice space can bring more value to the program. The risk-free rate is functioned as the growth rate in the binary tree model, and its increase can enlarge the demand quantity rising probability. The change of the riskfree rate is not drastic in real life;thus,it is important to determine the optimum value of rf.

6. Conclusions

(1) The existing product commonality indexes are summarized in this paper. Their limitations and complexity in the application to commercial aircraft family design are also analyzed. A component commonality index,based on the component decomposition structure, is then proposed,which can be used to evaluate the impact of commonality on the program value and time saving.

(2) A calculation model for the aircraft program value is proposed. The impact of commonality on R&D costs and time, manufacturing costs and time, and sale price is analyzed and quantified. A commonality evaluation strategy is also obtained,which comprehensively considers the program value and time saving.

(3) The operating costs are divided into two parts: the fuel cost and other cost (non-fuel cost). This paper focuses on the impact of commonality on the non-fuel cost,which is more conducive to the calculation of the aircraft value. The calculation model for the aircraft value takes the aircraft residual value into consideration to make the pricing of aircraft more reasonable and comprehensive.

Table 19 Commonality index of components of BWB-250C.

Table 20 Summary of parameters used in BWB-450/BWB-250C.

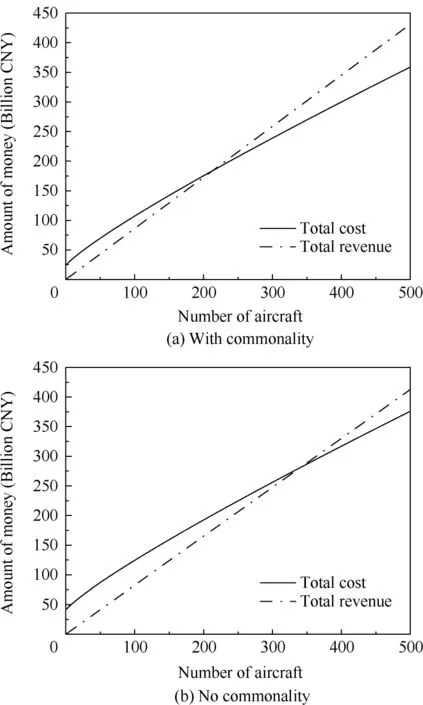
Fig. 11 Break-even analysis of BWB-250C.

Table 21 Key outputs of BWB-250C.

Fig. 12 BWB250-C program value: effect of commonality of fuselage.

Fig. 13 BWB250-C program value and sale price: effect of△(CAROC).

Fig. 14 BWB250-C program value: effect of β2 and β3.

Fig. 15 BWB250-C program value: effect of Td (decision period).

(4) The real option method and the binary tree model are used to forecast aircraft sale quantity, which ensures that the aircraft program value calculation considers uncertainty and flexibility. Three examples are used to verify the rationality and applicability of both the model for calculating the aircraft program value and the commonality evaluation strategy utilized in aircraft design process.Sensitivity analysis of the relevant parameters is also conducted. The value of parameters will influence the result drastically,so the determination of parameters should be as precise as possible.

Table 22 BWB250-C program value: effects of σ and rf.

(5) The accuracy of the model can be improved if more cost data (such as the R&D and the manufacturing costs of the aircraft) and market data (such as price and sales quantity of the aircraft) could be obtained. Extending the commonality index to assess the effect of the common software can increase the effectiveness of the index.

(6) The quantitative method of the aircraft performance could be analyzed and determined for the future commercial aircraft family design. The problem of the performance and economic benefits of the aircraft family can be studied to make the commonality valuation model more comprehensive.