正弦、余弦定理的十五类变式在高考中的灵活应用
■四川省巴中中学 肖 斌(特级教师)
高考注重对实践能力和核心素养的考查,正弦、余弦定理的变式及其活用较好地体现了这一精神,成为历年来高考数学试卷中常考不衰、常考常新的经典题型。下面进行系统总结,撩开其神秘“面纱”。
一、正弦定理的七类变式及其活用
在三角形中,各边与它所对角的正弦的比值相等,且该比值等于这个三角形外接圆的直径。即在△ABC中,有(R为△ABC外接圆的半径),这便是著名的正弦定理。正弦定理揭示了三角形中三条边a,b,c和三个角A,B,C及其外接圆半径R这7个元素间的动态等量关系,本身是一个比例式,若灵活运用比例性质,充分挖掘比值的几何意义,则有以下几类功效独特的变式。
变式1正弦定理的等积变形:asinB=bsinA,bsinC=csinB,asinC=csinA。
例1(2018年天津卷理数)在△ABC中,内角A,B,C所对的边分别为a,b,c。已知
(1)求角B的大小;
(2)设a=2,c=3,求b和sin (2A-B)的值。
解析:(1)在△ABC中,由正弦定理,可得bsinA=asinB。
因为B∈(0,π),所以B=
(2)在△ABC中,由余弦定理及条件a=2,c=3,B=,得b2=a2+c2-2accosB=7,故b=7。
因为三边中a最小,所以A必为锐角。
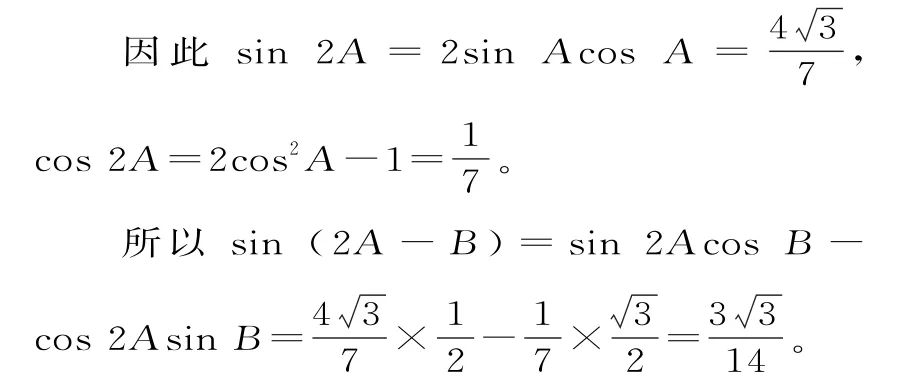
变式2正弦定理的“知三求一”变形:
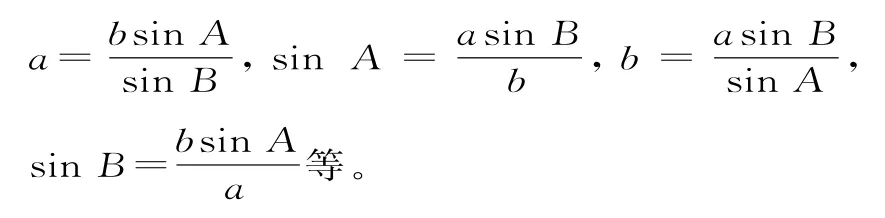
例2(2018年高考浙江卷)在△ABC中,角A,B,C所对的边分别为a,b,c。若a=,b=2,A=60°,则sinB=____,c=____。
解析:由正弦定理,得
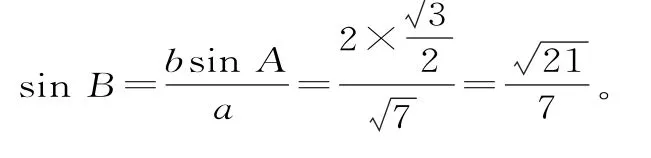
由余弦定理a2=b2+c2-2bccosA,得=22+c2-2·2·c·cos 60°,即c2-2c-3=0,解得c=3或c=-1(舍去)。
感悟:“已知两边和其中一边的对角,解三角形”(简称“边边角”问题),既可用正弦定理求解,也可由余弦定理求解。
变式3正弦定理的更比变形:
例3锐角△ABC的内角A,B,C的对边分别为a,b,c,若B=3A,则的取值范围是_____。

由A+B+C=180°,且B=3A,得C=180°-4A。
因为△ABC为锐角三角形,所以A,B,C三个角均为锐角,即同时满足:0<A<90°,0<B=3A<90°,0<C=180°-4A<90°。
解得22.5°<A<30°。
所以cos 30°<cosA<cos 22.5°,

感悟:这是一道精彩题目,能力要求极高:一是需用正弦定理进行边角互化;二是需用二倍角公式推导三倍角公式;三是需正确诠释锐角三角形的定义,即由锐角三角形的三个内角都是锐角求得角A的范围;四是需用余弦函数单调性及降幂公式求出的取值范围。
变式4正弦定理的合比变形:

例4(2017年郑州市高三一测理数试题改编)已知非等腰△ABC的外接圆的直径为,角A,B,C所对的边分别为a,b,c,并且C=60°。
(2)若a+b=ab,求△ABC的面积。

由余弦定理c2=a2+b2-2abcosC,得4=a2+b2-ab=(a+b)2-3ab。
又a+b=ab,所以(ab)2-3ab-4=0。
解得ab=4或ab=-1(舍去)。

感悟:出现分子和分母中系数对应结构时,可考虑合比变形处理,即
变式5正弦定理的连比变形:a∶b∶c=sinA∶sinB∶sinC。
例5在△ABC中,sinA∶sinB∶sinC=3∶5∶7,则这个三角形的最大角为_____。
解析:设△ABC中角A,B,C的对边分别为a,b,c,由正弦定理得a∶b∶c=sinA∶sinB∶sinC=3∶5∶7。设a=3k,b=5k,c=7k(k>0),易知最大角为C。由余弦定理得因为0°<C<180°,所以C=120°。故这个三角形的最大角为120°。
变式6正弦定理的化边为角变形:a=2RsinA,b=2RsinB,c=2RsinC(R为△ABC的外接圆的半径)。
例6(2013年全国Ⅱ理数)△ABC在内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB。
(1)求B;
(2)若b=2,求△ABC面积的最大值。
解析:(1)由正弦定理得a=2RsinA,b=2RsinB,c=2RsinC(R为△ABC外接圆的半径)。
代入已知得2RsinA=2RsinB·cosC+2RsinC·sinB。
也即sinA=sinBcosC+sinCsinB。
因为sinA=sin[π-(B+C)]=sin(B+C),所以sin (B+C)=sinBcosC+sinCcosB。
则cosBsinC=sinCsinB。
因为C∈(0,π),sinC≠0,所以tanB=1。又因为B∈(0,π),所以B=。
(2)由余弦定理得b2=a2+c2-2accos,即a2+c2≥2ac,当且仅当a=c时取等号,所以4≥(2-)ac。
解得ac≤4+。
所以△ABC的面积为
故△ABC面积的最大值为+1。
变式7正弦定理的化角为边变形:(R为△ABC外接圆的半径)。
例7(2018 年高考全国Ⅰ卷文数)△ABC的内角A,B,C的对边分别为a,b,c,已知bsinC+csinB=4asinBsinC,b2+c2-a2=8,则△ABC的面积为____。

解法二(化边为角)由正弦定理得a=2RsinA,b=2RsinB,c=2RsinC(R为△ABC外接圆的半径)。
代 入 已 知 得 2RsinB· sinC+2RsinC·sinB=4·2RsinA·sinBsinC。
因为2RsinBsinC≠0,所以两边同时除以2RsinBsinC,得sinA=
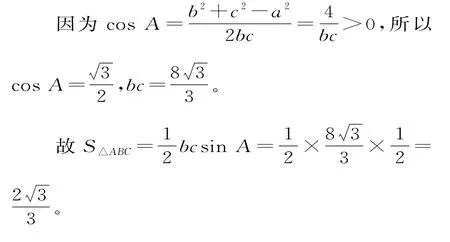
二、余弦定理的八类变式及其活用
在△ABC中,由余弦定理a2=b2+c2-2bccosA,可得以下八类有用的变形公式。
变式1余弦定理的角边互化变形:

此变式更清晰地表达了三角形中角与边的转化关系,从左往右可将角的关系转化为边的关系,从右往左则将边的关系转化为角的关系。
例8(2016 年全国Ⅲ卷文数)在△ABC中,B=,BC边上的高等于,则cosA=( )。
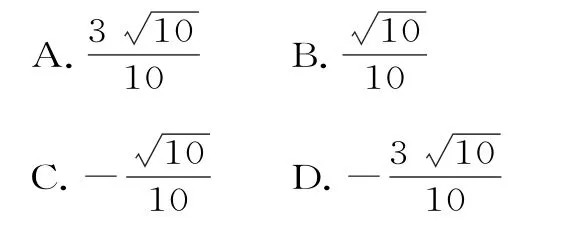
解析:设△ABC中角A,B,C的对边分别为a,b,c,由题意得:

变式2余弦定理的移项变形:b2+c2-a2=2bccosA。
此变式可有效处理题目中含有“b2+c2-a2”型信息(即“已知两边的平方和与第三边的平方差”)及相关面积型问题。
例9(2018 年全国Ⅲ卷理数、文数)△ABC的内角A,B,C的对边分别为a,b,c,若△ABC的面积为,则C=( )。

解析:由余弦定理得a2+b2-c2=2abcosC。于 是
又S△ABC=,所以cosC=sinC。
因为C∈(0,π),所以C=,选C。
变式3余弦定理的配方变形:a2=(b+c)2-2bc(1+cosA),a2=(b-c)2+2bc(1-cosA)。
此变式对处理有关“两边之和(差)、积及夹角,求第三边”型问题十分有用。
例10(2017 年全国Ⅰ卷理数)△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长。
解析:(1)由题设得
显然sinA≠0,故sinBsinC=
(2)由题设及(1)得cos(B+C)=cosBcosC-sinBsinC=
因为B+C∈(0,π),所以B+C=
故A=
由a=3 及,得bc=8。
由余弦定理得a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)。
变式4余弦定理的主元变形:b2-(2ccosA)b+(c2-a2)=0,c2-(2bcosA)c+(b2-a2)=0。
此变式的实质是将等式视为其中一边的一元二次方程,因此根的判别式与韦达定理可派上用场、大显身手。解决“已知三角形的两边与其中一边的对角,求第三边”(即“边边角”)型问题时,许多同学常拘泥于正弦定理去思考,其实用“余弦定理的主元变形”去处理更加简捷,应引起我们足够的重视。
例11根据下列条件,判断△ABC解的个数:

解析:由余弦定理得c2-(2bcosA)c+(b2-a2)=0。(1,则,c1c2=4>0,二次方程有两个不等正根,故此三角形有两个解。
(3)c2-10 3c+84=0,则,二次方程无实根,此三角形无解。
变式5余弦定理中的两边之比变形:

此变式可巧妙、快捷地处理题目中含有“两边之比”型整体信息。
例12(2005 年高考天津卷)在△ABC中,角A,B,C所对的边分别为a,b,c。设a,b,c满足b2+c2-bc=a2和,求角A和tanB的值。
解析:由已知得b2+c2-a2=bc,由余弦定理,得b2+c2-a2=2bccosA。

感悟:本题由正弦定理的变式去处理也很方便,过程类似于“正弦定理的变式及其活用”中的例3,同学们可以试一试。
变式6三角形中的射影公式:

此变式用正、余弦定理均不难证明,必修五课本虽以习题形式呈现,但高考中以此为背景的试题却层出不穷。
例13(2016 年全国Ⅰ卷理数)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c。
(1)求C的值;
(2)若c=,△ABC的面积为,求△ABC的周长。
解析:(1)方法一(用正弦定理及和角公式)由已知及正弦定理得2cosC(sinAcosB+sinBcosA)=sinC,即2cosCsin (A+B)=sinC。
因为A+B+C=π,且A,B,C∈(0,π),所以sin (A+B)=sinC>0。

方法二(用三角形中的射影公式)由射影公式得acosB+bcosA=c。
又因为2cosC(acosB+bcosA)=c,所以2ccosC=c,cosC=
因为C∈(0,π),所以C=
(2)由余弦定理得c2=a2+b2-2ab·cosC,即
整理得(a+b)2-3ab=7。

则(a+b)2-18=7,a+b=5。
△ABC的周长为a+b+c=5+7。
变式7向量的数量积与余弦定理的结合变形:在△ABC中,若角A,B,C的对边分别为a,b,c,则:
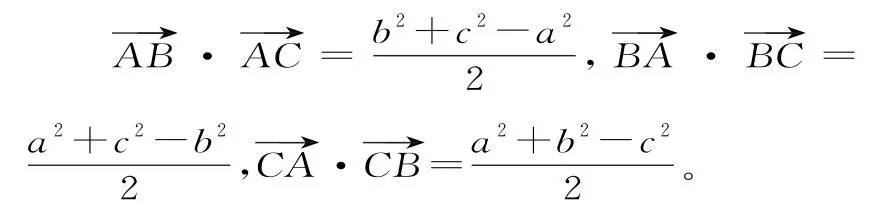
例14若不同的三点A,B,C满足=3∶4∶5,则这三点可以( )。
A.组成锐角三角形
B.组成直角三角形
C.组成钝角三角形
D.在同一直线上
解析:解法一(利用向量的数量积与余弦定理的结合变形公式)


于是a2+b2-c2=6t,b2+c2-a2=8t,a2+c2-b2=10t。
解得a2=8t,b2=7t,c2=9t,t>0。
显然角C最大。

最大角C为锐角,故不同的三点A,B,C组成锐角三角形,选A。

易见t<0,角C最大。仿照解法一,可知不同的三点A,B,C组成锐角三角形,选A。
变式8正、余弦定理的结合变形:sin2A=sin2B+sin2C-2sinBsinCcosA。
将正弦定理的变式直接代入余弦定理即得,此变式在解决形如sin2α+sin2β-2sinαsinβcosγ(α+β+γ=180°)的 求 值 问题时“一剑封喉”,别开生面。
例15(全国高中联赛题)求值:cos210°+cos250°-sin 40°sin 80°。
解析:原式可变形为sin280°+sin240°-2sin 80°sin 40°cos 60°,若将80°,40°视为三角形的两内角,则另一内角为60°,故原式=
- 中学生数理化(高中版.高二数学)的其它文章
- 正弦定理的八大功能
- 用放缩法证明数列不等式的策略
- 精讲解三角形考点
- 喜报
- 全国名校解三角形测试题(A卷)
- 全国名校数列测试题(B卷)

