基于两阶段遗传算法确定权重的城市信息化模糊综合评价研究

王宁宁 赵晓永 陈锐

[摘    要] 我國政府网站经过20年的发展建设已取得一定成就，通过介绍我国政府网站建设相关政策，将政府网站建设历程划分为初始起步、快速发展、加强服务和互联网+政务四个阶段，总结出我国政府网站发展的特征，即资源集约化、服务广泛化、流程一体化、制度规范化、应用创新化、公众参与化、监督常态化，并从推动政府数据开放、开展一站式服务平台建设和拓展服务渠道和手段三个方面对我国政府网站建设提出意见，以期为我国政府网站建设提供参考。

[关键词] 城市信息化;模糊综合评价;投影寻踪;遗传算法;多目标规划

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2019. 17. 068

[中图分类号]  TP312    [文献标识码]  A      [文章编号]  1673 - 0194（2019）17- 0173- 05

0      引    言

城市信息化又称数字信息化，是指在城市的发展运行管理等各个层面和各个环节，以信息技术为基础，采用计算机网络通信和软件等各种信息技术为主的现代高科技，对城市的各类信息资源进行开发管理，提高城市的运行管理水平，增强城市的竞争力，实现城市的基础地理，基础设施和基础功能的全部数字化，网络化智能化和可视化，加速城市现代化的发展过程。

城市信息化是区域信息化的核心龙头，城市信息化程度和水平是衡量一个城市经济、社会发展综合实力和发展水平的重要标志，是国家信息化和我国城市现代化战略的重要组成部分，因此客观合理的评价城市信息化水平是城市信息化建设的重要任务之一。

国内外关于城市信息化评价方面的研究正在蓬勃发展，在信息化测评研究方面取得了诸多成果。国外主要针对的是国家区域信息化的测评，针对城市信息化的测评研究还比较薄弱。国内随着城市化进程的加快和城市信息化的发展，对城市信息化评价的研究逐渐兴起，国内研究主要集中城市信息化水平指标体系的研究上，研究成果比较丰富。李小青  等提出一套城市信息化评价指标体系，应用熵权系数法构建城市信息化评价模型[1]。李晨光  等提出了基于群决策方面的城市信息化发展水平评估模型[2]。

上述研究存在着共同的不完善之处：（1）指标权重的确立是评价的关键，以往指标的权重过于依赖个人的主观经验，不能反映指标的数据特征。（2）传统的评价方法很难将指标的定性性与定量性统一起来进行综合评价，降低了评价的效果。本文在前人研究的基础上通过建立多目标规划，将主观赋权与客观赋权相结合，通过遗传算法计算指标的权重，并采用多层模糊综合评价方法，将城市信息化的定性与定量指标进行综合分析，使城市信息化评价更加客观准确。

1      城市信息化评价指标的确立与数据来源

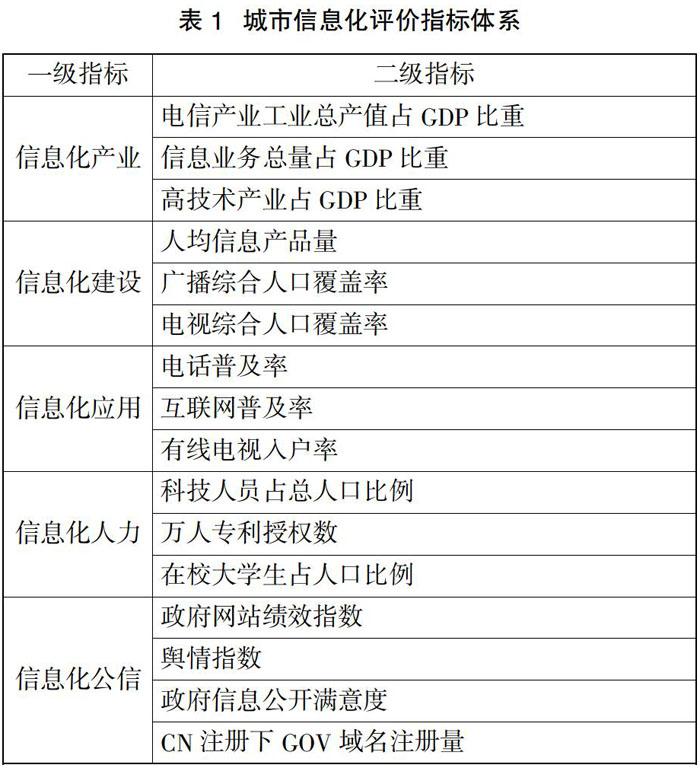
不同的专家对信息化评价体系的指标构成研究的侧重点不同，由于城市信息化评估体系的多因素、多层次与综合性，信息化指标的选取必须能够反映信息在支持、响应和公信等多个方面的能力水平，本文借鉴现有的统计体系和统计资料，在各专家学者、信息产业部门以及权威部门建立的指标体系基础上，采用频度统计计划，理论分析和主成分分析等方法对指标进行选择和筛选[3]，建立了5个层次共包括20项具体指标的城市信息化评价体系（见表1）。

注：信息业务总量（通信业务总量+电信业务总量+邮政业务总量）;信息产品产量（集成电路+程控交换机+移动通信手机+微机+电视机）;电话普及率（电话普及率+移动电话普及率）。上述数据主要来源城市统计年鉴，中国信息年鉴，中国互联网发展状况统计报告，中国网络舆情指数年度报告以及国家统计局网站等

2      评价方法的选择

2.1   指标的处理与无量纲化

为消除量纲的影响，处理原始指标矩阵R（xij）mn（i=1，2，…，m，j=1，2，…，n，m为评价对象的总个数，n为评价指标的个数）。对于定量评价指标x′ij（i=1，2，…，m，j=1，2，…，n）根据不同的评价指标类型进行无量纲处理：

对于定性指标，需要进行量化和指标标度，采用Macaimmonm两极比例方法，将定性指标转化为定量指标，然后根据上述定量指标的方法进行无量纲处理。

2.2   基于遗传算法的指标权重计算

利用遗传算法求解上述非线性规划[5]，得到城市评价指标体系系统的初始最优权重Ω0=（ω0ki，k=1，2，…，l，i=1，2，…，mk）。

第二阶段，建立多目标权重规划模型P2。

目标函数（1）表示最大化每个评价对象加权评价指标值，目标函数（2）表示最小化指标权重与系统初始权重偏离度。约束条件（3）表示权重和为1，约束条件（4）表示权重在一定范围内变化。针对模型的特点，采用多目标遗传算法进行求解，求解流程见图1，得到系统权重ωij，根据式（6）求平均得到系统的最终优化权重ωi。

遗传算法的求解流程图见图1。

2.3   建立模糊综合评价模型[6][7]

U11   U12   U13U21   U22   U23U31   U32   U33U41   U42   U43U51   U52   U53（7）

由上述評价指标体系构造模糊判断矩阵Ri（rij）m×n，其中m为评价对象的个数，n为一级指标下xi各二级指标的个数，根据式（3）Si=ωij×Ri得到更高一级的评价向量，并组成更高一级的模糊评价矩阵R=（S1，S2，…，Si，…，Sn）T，将一级评价指标权重ωij以及一级模糊矩阵R代入公式（8）得到最终评价向量B。

2.4   综合评价的进一步分析[8][9]

定义一个临界值ε，若ηij≥ε，可以认为一级指标Xi和Xj具有紧密的相关关系，从另一个角度分析，指标Xi与指标Xj可以相互影响[10]，其影响力对城市信息化的评价以及信息化建设提供良好的政策建议。

3      模型的应用实证分析

对城市A 2013年至2017年历年的信息化发展水平进行评价，指标体系的构建参照第二部分信息化评价指标体系，由五个一级指标和十五个二级指标组成，通过模糊综合评价判断城市A在不同时间段的信息化水平，为城市A下阶段的信息化工作提供科学的依据。

第一步，将2006-2010年的原始指标矩阵进行无量纲化处理投影寻踪-多目标规划-遗传算法（PPM-MOP-GA），采用VS2010与Matlab混合编程，调用CA工具箱计算得到的二级指标的权重见表2，一级指标的权重向量为ω=[0.252，0.214，0.182，

0.173，0.179]。

第二步进行综合评价，根据二级指标权重向量计算二级指标模糊评价矩阵，用Matlab进行矩阵运算，得到最终评价结果（进行归一化处理）S=[0.100，0.155，0.328，0.336，0.431]，b1

由文献[11][12][13]所提供的层次分析法在本文城市信息化评价指标体系基础上进行评价，得到的一级指标的权重向量为w=[0.305，0.217，0.202，0.169，0.087]，对比本文所提出的多目标规划所得到的系统一级指标权重可以看到在信息化人力和信息化公信这两个指标的权重赋值上存在显著的不同，层次分析法更加关注的是信息化人力指标的重要性，而本文得到的最终权重结果显示信息化公信指标相对信息化人力指标更加重要，根据近年来城市信息化建设越来越注重电子政务以及政府信息公信力，可以看到本文所得到的权重更加合理，因此对城市信息化的评价结果更加符合城市的发展和建设规律。

第三步进行模糊综合评价的进一步分析，将各年份的5个一级信息评价指标的相对隶属度进行归一化处理，计算模糊集两两之间的贴近度见表3所示（其中具有绝对的相关关系用“—”表示）。

由此可以分析出城市信息化支撑，响应和公信是联动发展的，信息化建设是基础，提高信息化建设可在一定程度上影响信息化的应用水平和信息化的产业发展水平，信息化人力资源的情况也可以影响信息化的应用，信息化的应用水平影响城市信息化的公信力，因此，提高城市的信息化水平尽可能地加强对城市信息化建设和城市信息人力资源的投入，从而提高城市信息化的应用水平和公信力，在关注城市化应用水平提高的同时，注重城市信息技术的转移和产业化发展。

4      结    论

本文将城市信息化的定性指标纳入城市信息化评价体系中，采用模糊综合评价方法实现城市信息化定性与定量性的综合评价，在此基础上建立两阶段多目标权重规划模型确定指标的权重，并且以投影寻踪方法确立评价系统的初始权重和衡量权重，利用多目标遗传算法求解系统最终权重，排除了对选择的因素赋予权重的主观随意性，是评价结果更加合理，更加客观，选取城市A连续五年的数据进行评价，评价结果良好并且符合城市信息化的发展趋势。

主要参考文献

[1]李晓青， 郑蓉. 基于熵权系数法的城市信息化测评研究[J]. 情报杂志，2007，12（3）： 184-190.

[2]李晨光， 王春新. 基于群决策方法的城市信息化发展水平评估模型[J]. 情报杂志， 2009， 28（3）： 204-206.

[3]李钢， 田丽娜， 齐二石. 基于BP神经网络和遗传算法的企业信息化评价研究[J]. 科技进步与对策， 2008， 25（5）： 129-132.

[4]刘合香，徐庆娟. 区域洪涝灾害风险的模糊综合评价与预测[J].灾害学，2007， 22（4）： 38-42.

[5]伍爱友， 施式亮， 王从陆. 基于神经网络和遗传算法的城市火灾风险评价模型[J]. 中国安全科学学报， 2006， 16（11）： 108-113.

[6]王晓明， 王浣尘，陈明义. 一种新型城市信息化发展评价方法的建立[J].系统工程理论方法应用， 2000， 9（4）： 277-281.

[7]金菊良， 魏一鸣， 丁晶. 基于组合权重的系统评价模型[J]. 数学的实践与认识， 2003， 33（1）： 51-58.

[8]谢季坚，刘承平. 模糊数学方法及其应用[M]. 武汉：华中科技大学出版社，2005： 144-145.

[9]柳玉鹏，曲世友. 组织内部员工信息安全胜任评价模型[J]. 运筹与管理，2014，23（1）：151-156.

[10]刘泽双，康英，章丹. 基于遗传算法的模糊综合评价法在科技人才创新能力评价中的应用[J]. 西安理工大学学报，2008， 24（3）： 376-379.

[11]宋远方.混合因素群体AHP方法及其通用软件[J].系统工程，1989，7（1）：66-71.

[12]黄德才，郑河荣.AHP方法中判断矩阵的标度扩展构造法[J]系统工程，2003，21（1）：105-109.

[13]Saaty T L.Decision Making with the AHP：Why is the Principal Eigenvector Necessary[J].European Journal of Operational Research， 2003，145（1）：85-89.