单箱连续刚构静载试验分析方法对比研究

汪贤安

（山西省交通科技研发有限公司，山西 太原 030032）

0 引言

为保证桥梁的使用安全，对其承载能力的鉴定是一个重要内容，连续刚构作为一种常见的大跨径预应力混凝土梁桥，其施工方便、跨越能力强、施工技术成熟，且外形也较为美观，使用众多，但是常规的杆系结构有限元分析方法无法精准地分析其横向受力情况，而实际工程中横桥向受力分析是重要的组成部分，梁格法与修正的单梁模型法可以有效地解决这一问题，本文采用大型有限元分析软件Midas Civil就单梁法、修正的单梁模型法和梁格法3种方法对连续刚构桥进行分析讨论[1]。

1 工程概况

本文以一座跨径（73.32+3×135+73.32）m的预应力混凝土连续刚构桥进行分析，该桥上部结构采用单箱单室截面；下部采用双薄壁空心墩，墩台基础采用灌注桩基础。设计荷载为公路-Ⅰ级；桥面净宽为净-2×11.75 m；地震动峰值加速度为0.15g。

该桥箱梁截面形式为单箱单室，顶板宽12.75 m，底板宽7 m，翼缘板悬臂长为2.875 m，截面高度由2.8 m渐变到8.5 m，截面如图1所示。

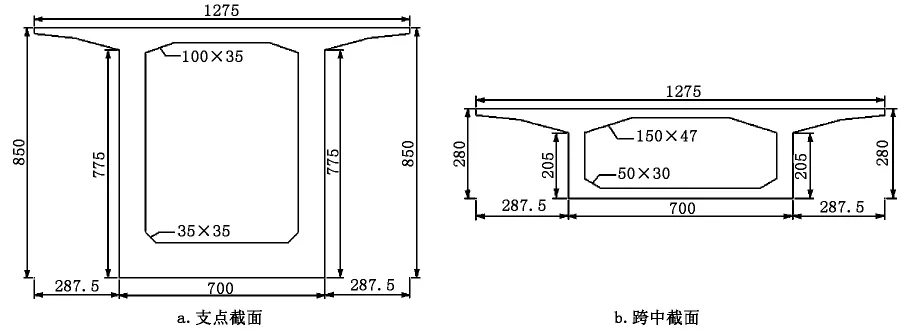
图1 截面形式（单位：cm）

2 结构分析原理

2.1 单梁法与修正的单梁模型法

单梁法是将梁体作为一根整体的单梁进行离散分析，无法考虑横向分布的影响，修正的单梁模型法是根据一些工程的内力分析，当箱梁的截面因畸变引起的扭曲应力很小时，活载引起的约束扭转正应力一般不超过活载弯曲正应力的15%，在计算箱型截面某个点的正应力时可以忽略箱梁的畸变效应，只考虑箱梁的纵向挠曲及约束扭转效应，在各肋板平均承受外荷载的基础上，把边肋所受的荷载最大增大15%，即偏载系数最大不超过1.15[2]，对于偏心距离的差异性没有描述，本文在单梁模型值的基础上乘以1.15系数作为不对称加载时偏载侧的结果，对应乘以0.85的系数作为非偏载侧的结果。该方法操作简单，内力的横向分布简单地按线性变化考虑，对于简单的箱型截面是可以的，但对于复杂的异型结构无能为力，特别是对于荷载偏心距与偏载系数取值之间的相关性并无明确规定。

2.2 梁格法

梁格法将桥梁上部结构模拟为若干个等效梁格，把分散在梁每一区段内的弯曲刚度和抗扭刚度集中在临近的等效梁格上，实际的纵向刚度与横向刚度集中于对应的纵横向梁格内[3]。在相同的外荷载作用下，任意一梁格内的内力应等于该梁格所代表的实际结构部分的单元内力，且变形与原结构相同。

3 梁格截面特性计算及计算模型[4]

3.1 截面特性计算

纵向构件抗弯刚度：EIy，其中Iy表示构件表面积对y轴的惯性矩；

纵向格构剪切刚度：GAs，其中As表示梁格代表的纵梁肋板面积；

纵向格构扭转刚度：GJx，其中Jx表示纵梁抗扭惯性矩与板抗扭惯性矩之和；

横向梁格刚度：

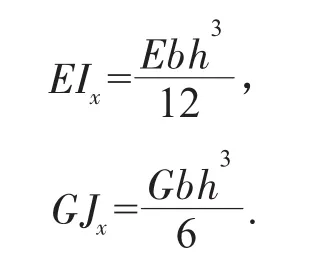
梁格划分基本原则应确保等效后结构的传力途径、作用方式、相对刚度不变。

3.2 结构离散模型

a）单梁模型采用平面杆件有限元法，根据桥梁的结构型式，采用Midas Civil对桥梁进行建模，将上部作为一根梁来考虑，有限元模型离散为361个节点，352个单元；模型结构如图2所示。

图2 单梁模型

b）梁格模型采用Midas Civil进行建模，本桥划分为2根纵梁，划分纵梁时沿箱梁截面中心线划分，以左右腹板为中心建立纵梁单元，横梁分为实际横梁和虚拟横梁两种，实际横梁依据实际横梁刚度建立单元，虚拟横梁采用工字型截面，顶、底板厚度按对应箱梁顶底、板厚度取。计算模型见图3。

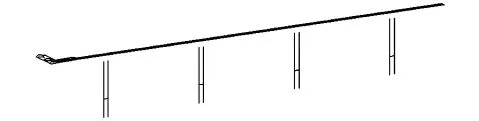
图3 梁格划分模型

4 分析工况

本文主要结合荷载试验对比3种方法在相同工况下产生的内力、变形，主要考虑车辆荷载，选取相邻的两跨来进行试验，根据需要设计以下几个工况：工况1：第6跨（边跨）最大正弯矩工况（偏载）；工况2：第6跨最大正弯矩工况（正载）；工况3：第7跨跨中最大正弯矩工况（偏载）；工况4：第7跨跨中最大正弯矩工况（正载）。

本次试验内力采用在箱梁内部粘贴应变传感器的方式采集，分别在第6、第7跨弯矩最大截面处设置测试截面；挠度采用精密水准仪测量。具体应变、挠度布置如图4，图4中“-”表示应变测点，“”表示挠度测点。

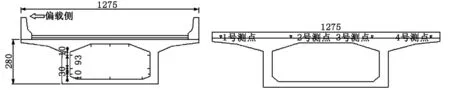
图4 测点布置

5 模型结果与实际数据对比

5.1 应力对比分析

判断桥梁承载能力的重要要素之一就是桥梁在外荷载作用下的应力变化规律，因此，需要通过对3种方法所得结果与实际值进行对比。通过工况1～工况4分别对第6跨和第7跨加载，计算出单梁模型值与梁格模型值，在单梁模型计算结果的基础上，对其进行修正，偏载侧乘以1.15的系数，非偏载侧乘以0.85的系数，得出修正的单梁模型值，3种方法所得理论值结合实测值绘制如图5所示，图中负值 表示拉应力。

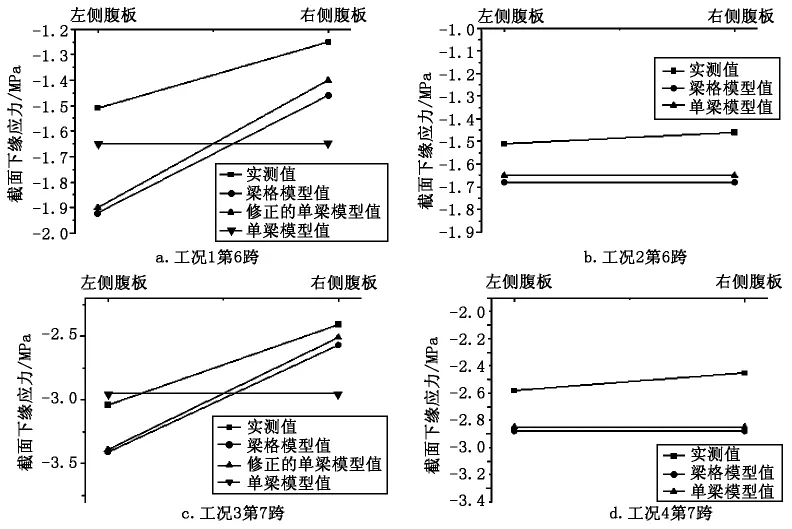
图5 测试截面应力值

通过图5可以看出，现场实测值均小于梁格模型与修正的单梁模型理论值，且梁格法与修正单梁模型法理论值相对误差较小，在变化趋势也基本相似，而单梁模型在对称加载情况下与梁格法极为接近，但无法考虑结构内力的横向分布情况，在做偏载工况时从单梁模型直接提取的计算值无法使用，需要加以修正后才能进行对比分析。

5.2 挠度对比分析

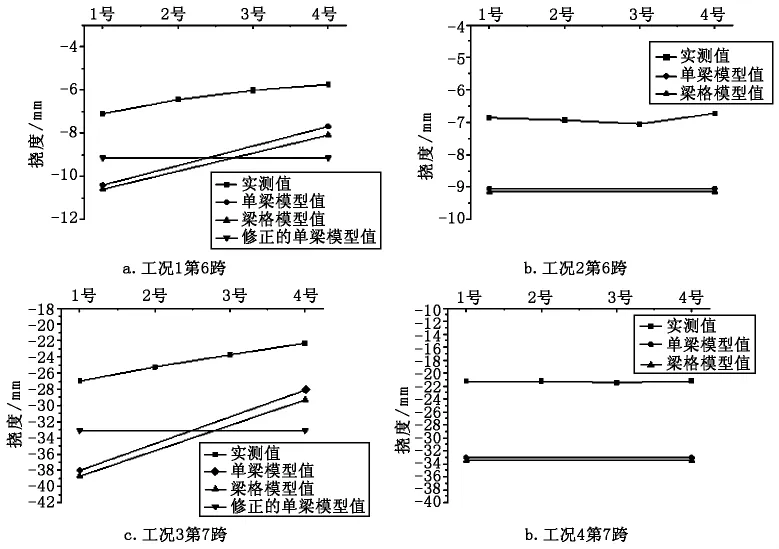
图6 测试截面挠度值

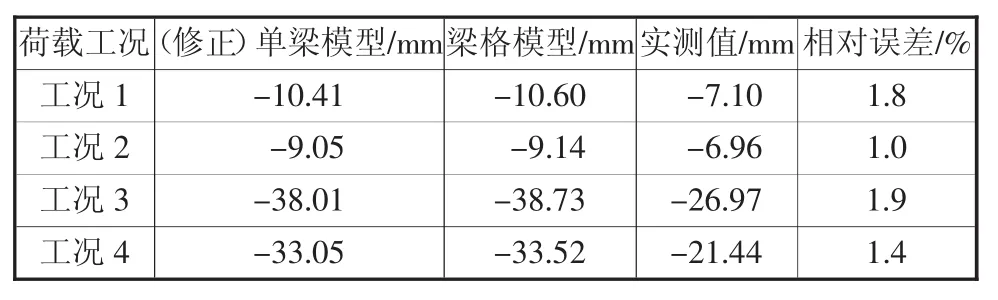
表1 各工况下最大挠度对比汇总

对比两种模型相同工况下的挠度值，由表1可以看出：

a）分析工况1，第6跨跨中截面在偏载作用下修正的单梁模型最大竖向挠度理论值为10.41 mm，梁格模型最大竖向挠度理论值为10.60 mm，实测值为7.1 mm。

b）分析工况2，第6跨跨中截面在正载作用下单梁模型最大竖向挠度理论值为9.05 mm，梁格模型最大竖向挠度理论值为9.14 mm，实测值为6.96 mm。

c）分析工况3，第7跨跨中截面在偏载作用下修正的单梁模型最大竖向挠度理论值为38.01 mm，梁格模型最大竖向挠度理论值为38.73 mm，实测值为26.97 mm。

d）分析工况4，第7跨跨中截面在正载作用下单梁模型最大竖向挠度值为33.05 mm，梁格模型最大竖向值为33.52 mm，实测值为21.44 mm；总体而言，两种模型理论值均大于实测值，二者之间相对误差较小，在2%以内。

通过与应力图相同的方式绘制出3种方法所得理论值与实测挠度值的对比图，见图6，由图6可以看出，工况1～工况4作用下实测值均小于3种方法理论值，且梁格模型值与修正的单梁模型值变化趋势基本相同，与正载作用下的单梁模型值也基本一致。梁格法和修正的单梁模型法可以较好地反映结构实际变形情况，而单梁模型直接得出的结果无法反映偏载工况下的结构变形情况。

6 结语

a）单梁模型对于对称加载结构理论计算值尚可，但对于偏载工况无法考虑，需要对结果进行修正。

b）修正单梁模型法与梁格法计算结果对于单箱单室结构较为接近，均可较好地满足本例结构类型的使用要求，在今后类似的工程中可选择这两种方式进行分析。